Циклические коды. Кодовые полиномы. Полиномиальная арифметика

1.

2.

Циклические коды. Кодовые полиномы.
Полиномиальная арифметика
• Линейный блоковый код U длины называется
циклическим, если наряду с любым своим
кодовым словом u=(u0, u1, … , un–2, un–1) (для
циклических кодов элементы удобнее нумеровать,
начиная с нуля, а не единицы) он содержит и его
циклический сдвиг u1=(un–1, u0, u1, … , un–3, un–2).
• Другими словами, циклический код содержит все
циклические сдвиги всех своих кодовых слов.
• Продуктивным
инструментом
изучения
и
построения
циклических
кодов
служит
полиномиальное представление (повторяющее zпреобразование в теории дискретных систем).
Кодовый полином, отвечающий кодовому вектору
u=(u0, u1, … , un–2, un–1), определяется равенством
u ( z ) un 1 z
n 1
un 2 z
n 2
n 1
... u0 ui z i .
i 0

3.

• Коэффициенты u0, u1, …, un–1 кодового
полинома – попросту элементы кодового слова
(для q-ичного кода – элементы поля GF(q)),
тогда как z – формальная переменная,
служащая не для обобщенного представления
произвольного элемента поля GF(q), а лишь
для указания своей степенью позиции того или
иного кодового символа как коэффициента
полинома. Обозначим по соглашению z0
как 1. Например, полином u(z)= z7+z5+z2+1

4.

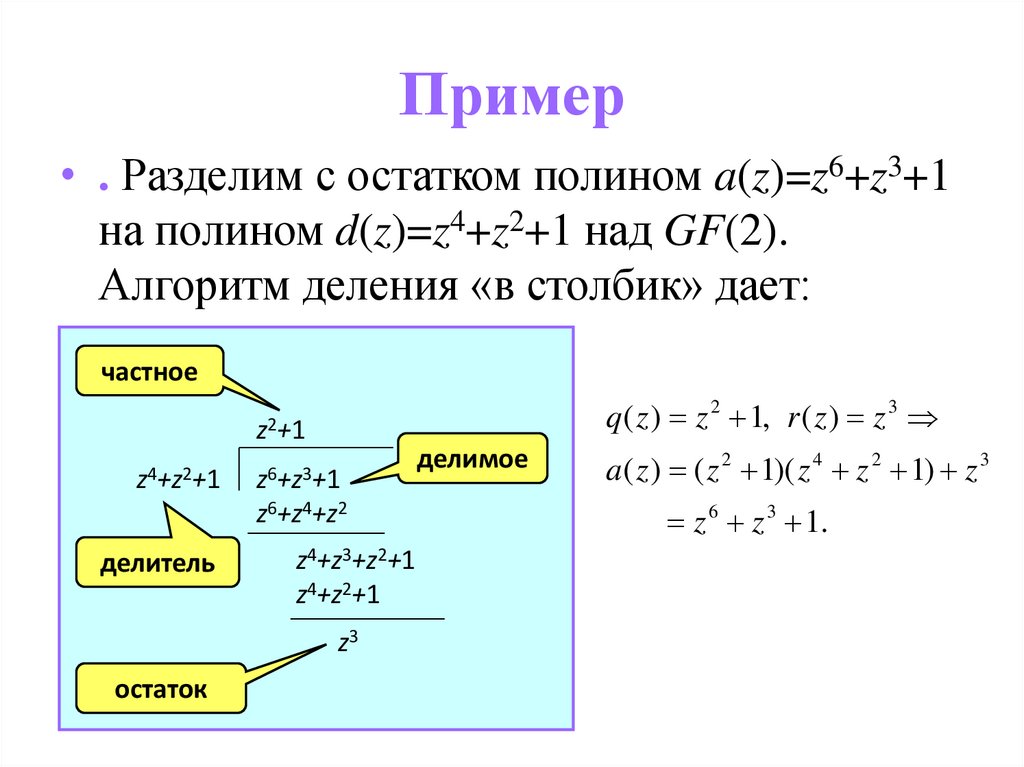
Пример
• Например, полином
• u(z)= z7+z5+z2+1
• означает, что в соответствующем кодовом
векторе u единицы стоят на позициях 0, 2,
5, 7, в то время как, все остальные
элементы равны нулю: u=(10100101).

5.

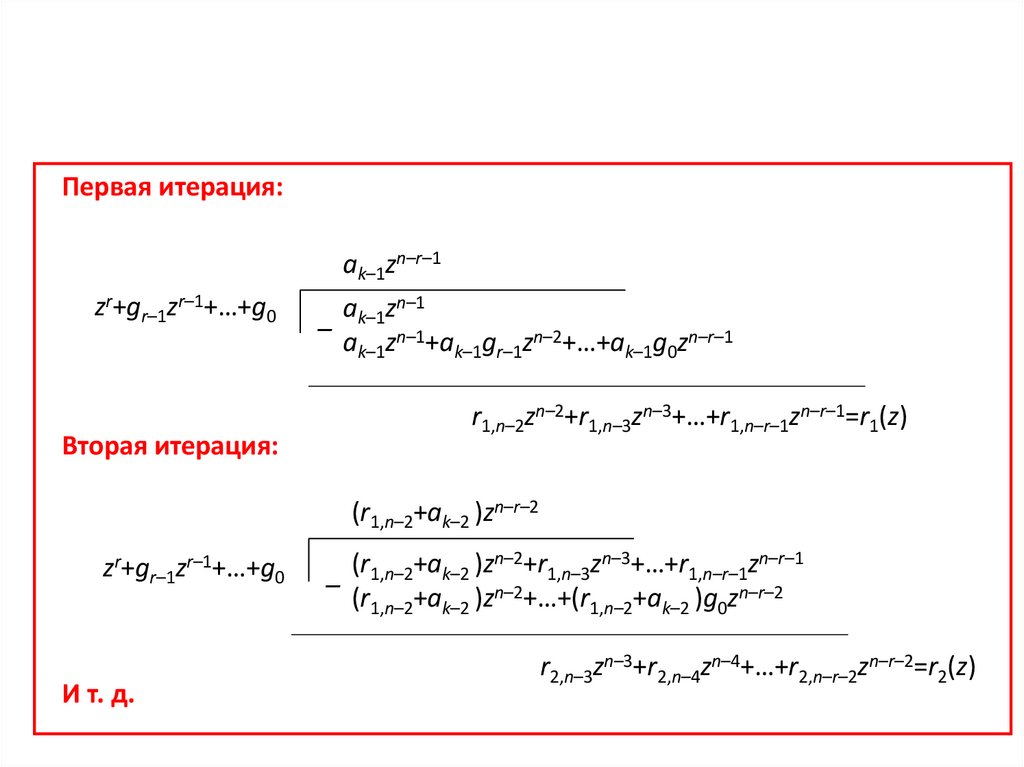
• Рассмотрим основные правила арифметики
формальных полиномов с коэффициентами из