FuzzyCLIPS – язык представления нечётких и неточных знаний

1.

FuzzyCLIPS – язык представления нечётких и неточных знаний
FuzzyCLIPS – популярная оболочка, позволяющая описывать нечёткие экспертные системы.
FuzzyCLIPS представляет собой расширение оболочки экспертной системы CLIPS в сторону
использования нечетких множеств.
Расширение улучшает возможности CLIPS, предоставляя возможности нечёткой
аргументации, которая полностью интегрирована с фактами и правилами ядра CLIPS.
FuzzyCLIPS дает возможность работать с чёткими, нечёткими, и комбинированными
аргументациями. Этот подход позволяет свободно смешивать нечёткие и нормальные условия,
в правилах и фактах экспертной системы. Система использует два понятия мягких
вычислений: нечеткость и неопределённость.
FuzzyCLIPS предоставляет полезную среду для разработки приложений использующих
нечёткую логику в системах принятия решений.
Язык FuzzyCLIPS, представляя собой расширение обычного CLIPS, является одним из языков
построения экспертных систем основанных на продукционной модели представления знаний.
При использовании этой модели знания представляются в виде
ЕСЛИ <условие(антецедент)>, ТО <действие(консеквент)>

2.

FuzzyCLIPS – язык представления нечётких и неточных знаний
Единственным существенным отличием FuzzyCLIPS от CLIPS является то, что основной
средой разработки является консоль, а все остальные окна режимов всплывающие, а не
дочерние, как в CLIPS.
Кроме этого редактор представляет собой отдельную программу, которую можно запускать
либо автономно, либо непосредственно из консоли, используя опции главного меню.
Практически все конструкции языка обычного в CLIPS остаются работоспособными. Поэтому
программы большинства примеров, разработанных в среде CLIPS, будут работать и в среде
FuzzyCLIPS.
Более того, знакомство и изучение FuzzyCLIPS надо начать именно с того, чтобы в этой среде
попробовать запустить свои старые программы в режимах трассировки и отладки. Это
позволит быстро привыкнуть к чуть измененной среде программирования.

3.

Интерфейс FuzzyCLIPS
Консоль
Редактор

4.

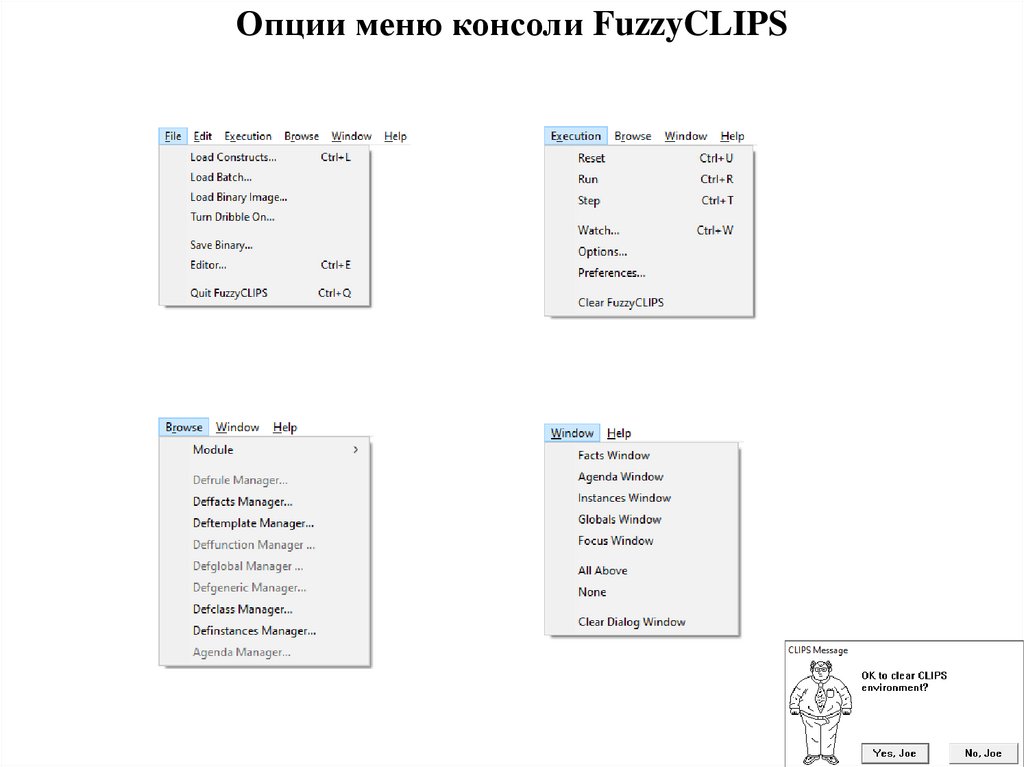
Опции меню консоли FuzzyCLIPS

5.

Запуск примеров в FuzzyCLIPS
Решение числового ребуса

6.

Запуск примеров в FuzzyCLIPS
Экспертная система по диагностике автомобиля

7.

Неопределенность в FuzzyCLIPS
Неопределенность возникает тогда, когда нет абсолютной уверенности в какой-то части
информации.
Степень уверенности в достоверности какой-либо информации обычно представляют четким
числовым значением в диапазоне 0 до 1, который получил название коэффициента доверия
или certainty factor (CF).
Значение коэффициент CF = 1 указывает, что эксперт или экспертная система очень уверены в
достоверности информации, в то время как CF = 0 указывает на то, что уверенность
абсолютно отсутствует.
В FuzzyCLIPS, конструкция факта расширена относительно CLIPS и состоит из двух частей:
из самого факта и его коэффициента доверия. В общем случае представление факта в
FuzzyCLIPS имеет следующий вид:
(fact) [CF <коэффициент_доверия>]
Так, например, факт
(prediction sunny) CF 0.8
показывает, что прогноз о солнечной погоде сделан с уверенностью в 80%, а если
коэффициент доверия в описании факта не указан, то FuzzyCLIPS предполагает, что погода
будет солнечная с уверенностью в 100%.

8.

Неопределенность в FuzzyCLIPS
Следует отметить, что аналогично можно определять коэффициенты доверия и для любых
правил базы знаний. Так, например, правило
(defrule flight-rule
(declare (CF 0.95)) ; коэффициент доверия для правила
(animal type bird)
=>
(assert (animal can fly))
)
представляет гипотезу о том, что с 95% уверенностью можно утверждать: «если животное
птица, то оно может летать». Аналогично фактам, если в операторе declare левой части
правила значение CF не заявлено, то оно по умолчанию предполагается равным 1.0.

9.

Неопределенность в FuzzyCLIPS
Рассмотрим следующее правило:
(defrule simple-rule
(declare (CF 0.7)) ; коэффициент доверия правила равен 0.7
(light_switch off) ; антецедент правила
=>
(assert (illumination_level dark)) ;нечеткий консеквент
)
Данное правило активируется в том случае, если в памяти системы будет задан факт
(light_switch off).
Запустим данный пример и добавим данный факт с указанием коэффициента доверия:
(light_switch off) CF 0.8
Тогда при согласовании правила simple-rule в рабочую область системы будет добавлен новый
факт: (illumination_level dark) CF 0.56
В процессе вывода, путем сопоставление образцов, система вычислить коэффициент доверия
нового факта на основе коэффициента доверия к исходному факту и коэффициента доверия
правила: CF=0,7 * 0,8.

10.

Пример экспертной системы с неопределенностями в фактах и правилах
В качестве примера работы со знаниями, в представлении которых есть неопределенность,
рассмотрим пример экспертной системы для диагностики болезней древесных растений.
Для удобства и наглядности сведём болезни и соответствующие им симптомы в таблицу.
Болезнь/
Симптомы
Мучнистая
роса
Налет на листьях
+
Шютте
Изменение окраса хвои
+
Образование спор на хвое
+
Парша
Пятна на листьях
+
Почернение побегов
+
Растрескавшаяся кора, с пузырями
Ожоги
+
+

11.

Пример экспертной системы с неопределенностями в фактах и правилах
На базе представленной ранее таблицы создадим четыре правила, описывающие каждую из
болезней древесных растений. Данные правила на основе информации, хранимой в рабочей
памяти системы, формируют диагноз и вычисляют степень его достоверности.
(defrule much_rosa ; мучнистая роса
(declare (CF 0.5))
(nalet yes) ; налет на листьях
=>
(assert (type much_rosa))
)
(defrule parsha ; парша
(declare (CF 0.5))
(or (pyatna yes) (pobegi_chern yes))
; пятна на листьях или почернение побегов
=>
(assert (type parsha))
)
(defrule shutte ; шютте
(declare (CF 0.7))
(and (hvoi_okras yes) (hvoi_spor yes))
; изменение окраса хвои и образование спор
=>
(assert (type shutte))
)
(defrule ozhogi ; ожоги
(declare (CF 0.8))
(and (kora_tresk yes) (pobegi_chern yes))
; Кора растрескавшаяся, с пузырями и
почернение побегов
=>
(assert (type ozhogi))
)

12.

Пример экспертной системы с неопределенностями в фактах и правилах
Следующие шесть правил дают возможность получить от пользователя степень его
уверенности, что на исследуемом образце присутствуют те или иные симптомы.
Эта информация сохраняется в рабочей памяти системы в качестве образцов, на основе
которых ЭС и делает свои заключения.
(defrule nalet ; налет на листьях
(declare (salience 100))
=>
(printout t "Есть ли на листьях налет? (0 to 1): ")
(bind ?cf (read))
(assert (nalet yes) CF ?cf)
)
(defrule pyatna ; образование пятен на листьях
(declare (salience 100))
=>
(printout t "Есть ли п9тна на листь9х? (0 to 1): ")
(bind ?cf (read))
(assert (pyatna yes) CF ?cf)
)
(defrule hvoi_okras ; изменение окраса хвои
(declare (salience 100))
=>
(printout t "Наблюдается ли изменение окраса хвои? (0 to 1): ")
(bind ?cf (read))
(assert (hvoi_okras yes) CF ?cf)
)
(defrule pobegi_chern ; почернение молодых побегов
(declare (salience 100))
=>
(printout t "Почернели ли побеги? (0 to 1): ")
(bind ?cf (read))
(assert (pobegi_chern yes) CF ?cf)
)
(defrule hvoi_spor ; образование спор на хвое
(declare (salience 100))
=>
(printout t "Есть ли споры на хвое? (0 to 1): ")
(bind ?cf (read))
(assert (hvoi_spor yes) CF ?cf)
)
(defrule kora_tresk ; растрескавшаяся кора с пузырями
(declare (salience 100))
=>
(printout t "Есть ли на коре пузыри и трещины? (0 to 1): ")
(bind ?cf (read))
(assert (kora_tresk yes) CF ?cf)
)

13.

Пример экспертной системы с неопределенностями в фактах и правилах
Заключение экспертной системы выдаётся на экран дисплея последним из правил:
; Функция get-cf возвращает коэффициент доверия (CF) факта
(defrule ShowResults
(declare (salience -100))
?f <- (type ?d)
=>
(printout t ?d " -> с доверием CF=" (get-cf ?f) crlf)
)
Проведём тестирование экспертной системы. На скриншоте приведена одна из возможных
консультаций пользователя с экспертной системой. По её результатам мы получили итоговое
распределение вероятностей той или иной болезни.
Примечание. В FuzzyCLIPS есть проблемы с отображением русской буквы «я». В связи с этим в программе буква «я»
заменена на цифру «9».

14.

Пример экспертной системы с неопределенностями в фактах и правилах
Более подробно рассмотрим процесс добавления фактов и формирование результатов. Для
этого в меню Execution выберем пункт Watch и поставим галочку напротив пункта Facts.

15.

Пример экспертной системы с неопределенностями в фактах и правилах
Запустим экспертную систему ещё раз. После каждого вопроса системы и ответа пользователя
в рабочую память добавляется соответствующий факт с указанным коэффициентом доверия
пользователю к тому или иному симптому.
Результирующее правило на базе данных коэффициентов вычисляет итоговые коэффициенты
доверия для всех болезней.

16.

Нечёткость в FuzzyCLIPS
Нечёткость возникает тогда, когда точно не ясна граница, отделяющая одну часть
информации от другой.
Такие понятия, как молодой, высокий, хороший или плохой по своей природе нечеткие. У них
отсутствует единая количественная оценка, которая позволила бы их определить.
Например, термин молодой. Одни полагают, что человек молодой в 25 лет, другие уверены,
что и в 35 лет человек молодой. Таким образом, понятие молодой не имеет точно
определенных границ и зависит от контекста, в котором это понятие рассматривают.
Представление такого рода информации в FuzzyCLIPS основывается на концепции теории
нечетких множеств.
В отличие от классической теории множеств, где имеют дело с объектами, принадлежность
которых тому или иному множеству точно описано, в теории нечетких множеств объект
принадлежит конкретному множеству с некоторой степенью уверенности.

17.

Нечёткость в FuzzyCLIPS
Формально, описание степени этой уверенности задается функцией принадлежности
μA : U → [0,1] ,
которая связывает число μA(x) в интервале [0,1] с каждым элементом х носителя нечеткого
множества U. Это число представляет степень уверенности в принадлежности х нечеткому
множеству A.
Например, нечеткое понятие young (молодой) может быть определено следующим образом:
возраст
25
30
35
40
45
50
степень уверенности
1.0
0.8
0.6
0.4
0.2
0
То есть, μyoung(25) = 1, μ young(30) = 0.8, …, μ young(50) = 0.
Эти выражения показывают степень нашей уверенности в том, что тот или иной возраст мы
относим к понятию молодой.

18.

Нечёткость в FuzzyCLIPS
Это может быть представлено графически в виде функции принадлежности:
Аналогично понятию молодой может быть определено понятие старый, которое будет
представлено своим нечетким множеством и описываться функцией принадлежности.
Оба эти понятия определят лингвистическую переменную «возраст», которая может
принимать из множества {молодой, старый} одно или сразу оба значения, но с разной
степенью доверия.

19.

Нечёткость в FuzzyCLIPS
Для лингвистической переменной должен быть определен носитель ее нечеткого множества.
Его еще называют базовое множество, числовая шкала или универсум.
Так, например, для переменной «возраст» (age) эта числовая шкала от 0 до 120,
обозначающая количество прожитых лет, а функции принадлежности будут определять,
насколько мы уверены в том, что конкретное количество лет можно отнести к
соответствующей категории возраста.
Нечеткие факты можно определить либо в объявлениях шаблонов, либо при их добавления в
рабочую память из командной строки или из правила при использовании функции assert.
(deftemplate age ;определение нечеткой переменной age
0 120 years
( (young (25 1) (50 0))
(old (50 0) (65 1))
)
)
(deffacts fuzzy-fact
(baby_has age young) ; это – нечеткий факт
)
(defrule myrule ; правило, которое согласовывает и добавляет нечеткие факты
=>
(assert (grandfather_has age old))
)
где young, old – это нечеткие термы, а age – лингвистические (нечеткая) переменная.

20.

Определение нечётких переменных в deftemplate
Каждая лингвистическая переменная ассоциируется с некоторым набором нечетких термов,
значение которых эта переменная принимает.
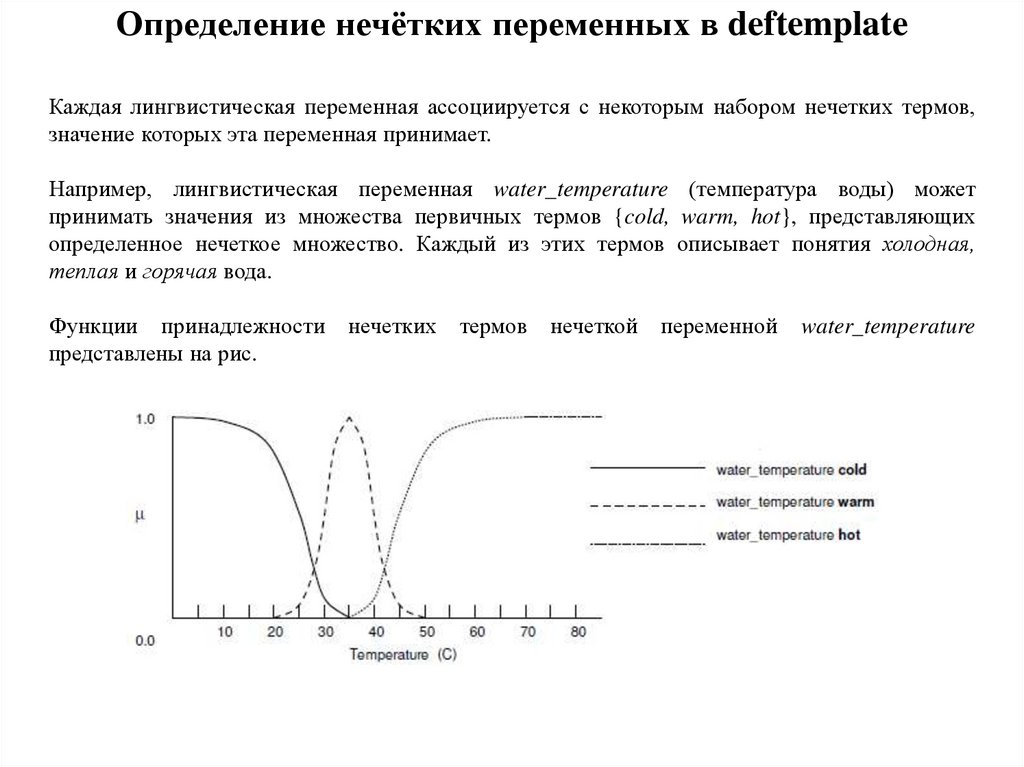
Например, лингвистическая переменная water_temperature (температура воды) может
принимать значения из множества первичных термов {cold, warm, hot}, представляющих
определенное нечеткое множество. Каждый из этих термов описывает понятия холодная,
теплая и горячая вода.
Функции принадлежности
представлены на рис.
нечетких
термов
нечеткой
переменной
water_temperature

21.

Определение нечётких переменных в deftemplate
Все нечеткие переменные должны быть определены до момента их использования в
конструкторе deftemplate.
Приведем пример для более подробного знакомства с использованием конструктора
deftemplate для описания в программе нечетких переменных.
Допустим, что в дальнейшем предполагается использовать позиционные факты вида:
(The_student <имя_студента> studies <оценка_знаний>)
При этом оценку знаний предполагается задавать не в числовой форме, а качественно:
{отлично (perfectly), хорошо (well), удовлетворительно (badly)}, когда каждый из термов
задается своим нечетким множеством, а лингвистическая переменная studies (учится)
определяется на базовом множестве от 1 до 5 баллов. Тогда описание нечеткой переменной
studies на языке FuzzyCLIPS будет иметь вид:
(deftemplate studies
1 5 ball
( (perfectly (4.5 0) (5 1) )
(well (3.5 0) (4 1) (4.75 0) )
(badly (1 1) (3 1) (3.75 0) )
))

22.

Определение нечётких переменных в deftemplate
Если это описание ввести в редакторе, добавить к нему еще одну строку
(plot-fuzzy-value t "+*o" nil nil (create-fuzzy-value studies badly))
а затем в окне редактора выделить набранный фрагмент и в меню Buffer выбрать пункт Batch
Selection, то в консоли FuzzyCLIPS будет получен следующий результат:
Последняя строка этого фрагмента служит для вывода графика функции принадлежности.

23.

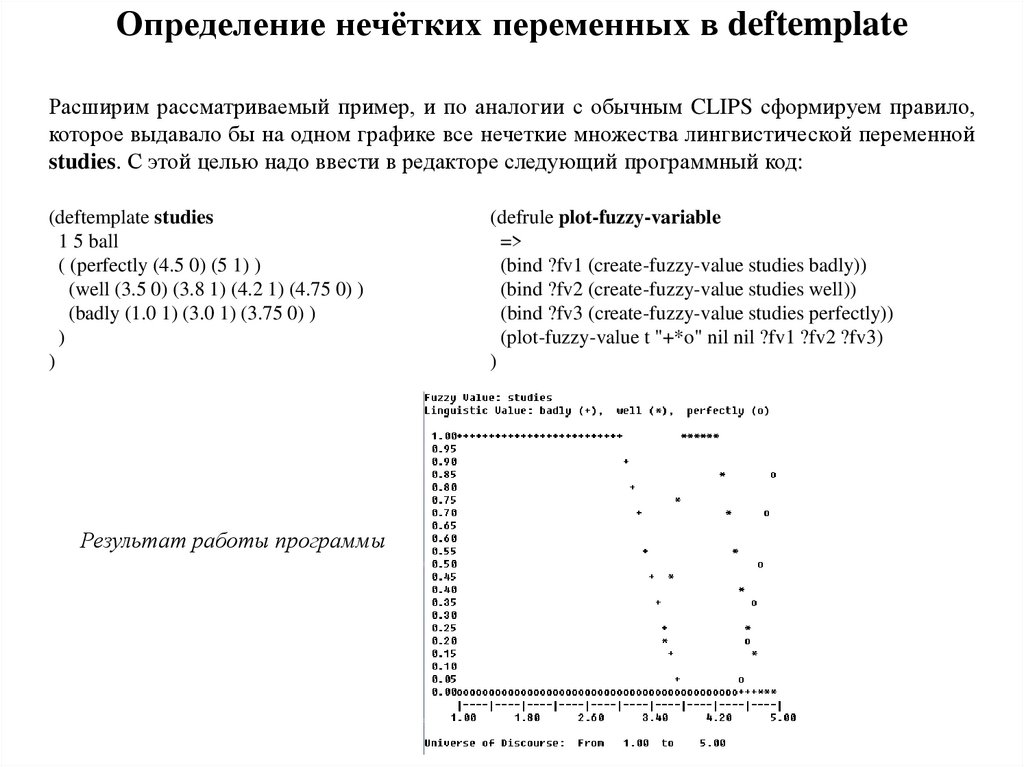
Определение нечётких переменных в deftemplate
Расширим рассматриваемый пример, и по аналогии с обычным CLIPS сформируем правило,
которое выдавало бы на одном графике все нечеткие множества лингвистической переменной
studies. С этой целью надо ввести в редакторе следующий программный код:
(deftemplate studies
1 5 ball
( (perfectly (4.5 0) (5 1) )
(well (3.5 0) (3.8 1) (4.2 1) (4.75 0) )
(badly (1.0 1) (3.0 1) (3.75 0) )
)
)
Результат работы программы
(defrule plot-fuzzy-variable
=>
(bind ?fv1 (create-fuzzy-value studies badly))
(bind ?fv2 (create-fuzzy-value studies well))
(bind ?fv3 (create-fuzzy-value studies perfectly))
(plot-fuzzy-value t "+*o" nil nil ?fv1 ?fv2 ?fv3)
)

24.

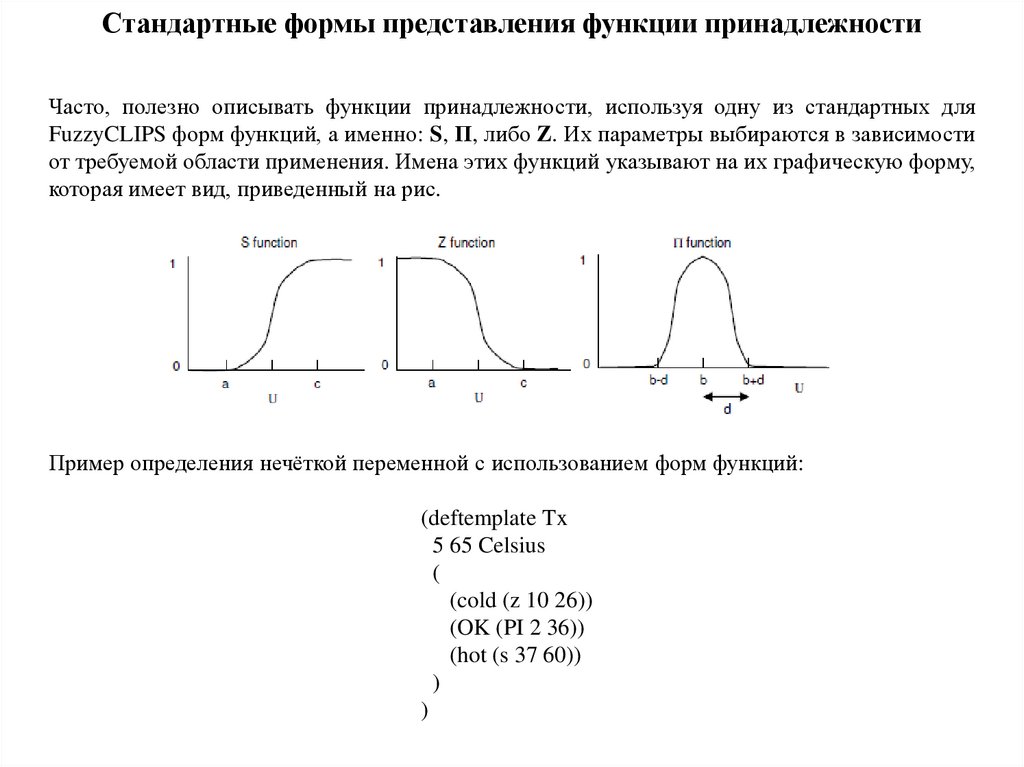
Стандартные формы представления функции принадлежности
Часто, полезно описывать функции принадлежности, используя одну из стандартных для
FuzzyCLIPS форм функций, а именно: S, Π, либо Z. Их параметры выбираются в зависимости
от требуемой области применения. Имена этих функций указывают на их графическую форму,
которая имеет вид, приведенный на рис.
Пример определения нечёткой переменной с использованием форм функций:
(deftemplate Tx
5 65 Celsius
(
(cold (z 10 26))
(OK (PI 2 36))
(hot (s 37 60))
)
)

25.

Лингвистические модификаторы нечетких множеств
Лингвистические модификаторы используются для создания нечетких множеств, являющихся
производными от некоторых ранее заданных. Например, если имеется нечеткое множество
«холодный», то на его основе с помощью лингвистических модификаторов можно получить
множества «очень холодный» или «более или менее холодный».
Имя
Описание действия
not
1-y
very
y**2
somewhat
y**0.333
more-or-less
y**0.5
extremely
y**3
intensify2
(y**2), если y in [0, 0.5]
1 - 2(1-y)**2, если y in (0.5, 1]
plus
y**1.25
norm
нормализует нечеткое множество, максимальное
значение будет равно 1.0 ( y = y*1.0/max-value )
slightly
intensify ( norm (plus A AND not very A))

26.

Лингвистические модификаторы нечетких множеств
Пример:
(deftemplate temp
0 100 C
(
(cold (Z 20 40))
(hot (S 60 80))
(freezing extremely cold)
)
)
(defrule plot-fuzzy-variable
=>
(bind ?fv1 (create-fuzzy-value temp cold))
(bind ?fv2 (create-fuzzy-value temp hot))
(bind ?fv3 (create-fuzzy-value temp freezing))
(plot-fuzzy-value t "+*o" nil nil ?fv1 ?fv2 ?fv3)
)

27.

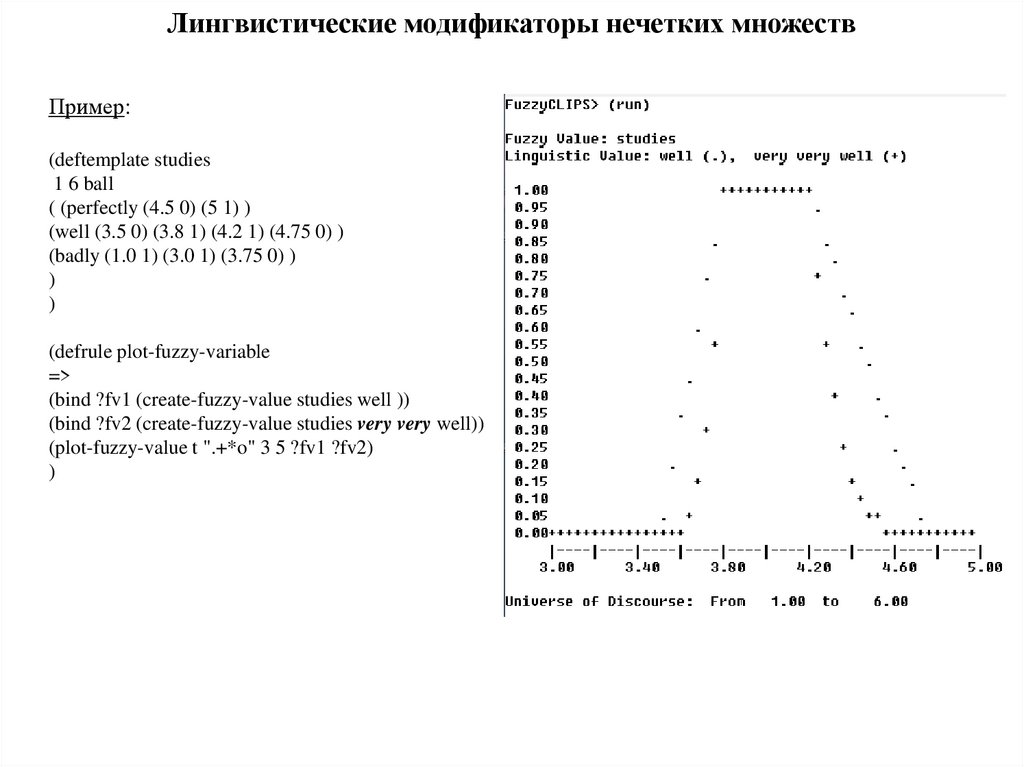
Лингвистические модификаторы нечетких множеств
Пример:
(deftemplate studies
1 6 ball
( (perfectly (4.5 0) (5 1) )
(well (3.5 0) (3.8 1) (4.2 1) (4.75 0) )
(badly (1.0 1) (3.0 1) (3.75 0) )
)
)
(defrule plot-fuzzy-variable
=>
(bind ?fv1 (create-fuzzy-value studies well ))
(bind ?fv2 (create-fuzzy-value studies very very well))
(plot-fuzzy-value t ".+*o" 3 5 ?fv1 ?fv2)
)

28.

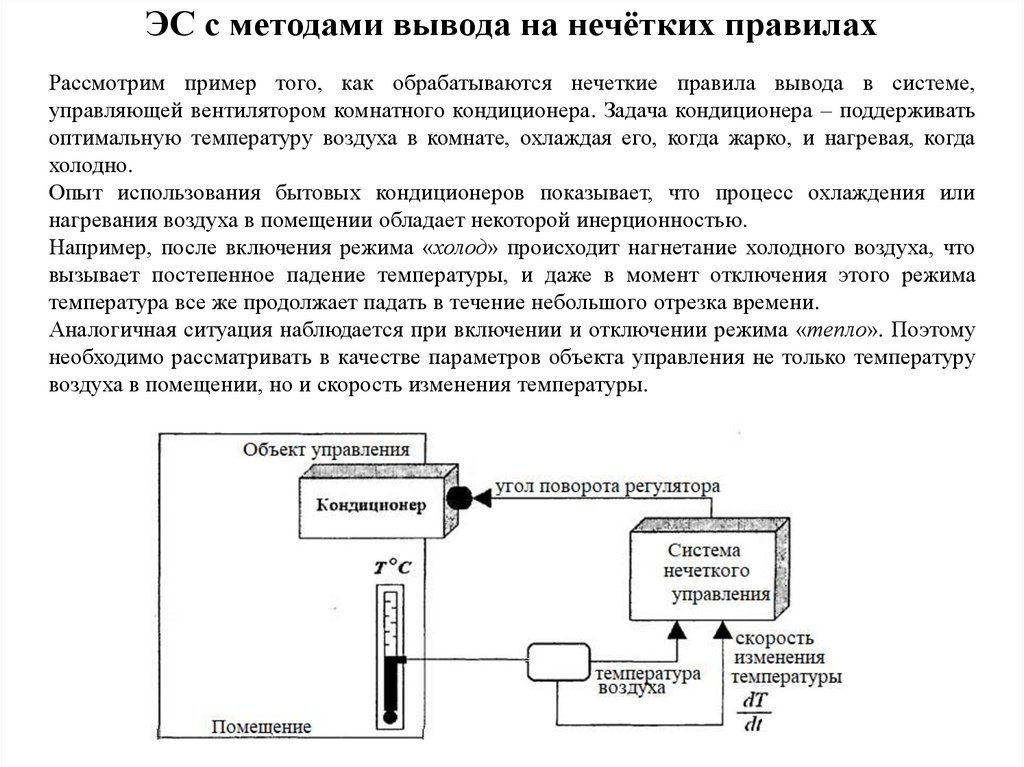
ЭС с методами вывода на нечётких правилах
Рассмотрим пример того, как обрабатываются нечеткие правила вывода в системе,
управляющей вентилятором комнатного кондиционера. Задача кондиционера – поддерживать
оптимальную температуру воздуха в комнате, охлаждая его, когда жарко, и нагревая, когда
холодно.
Опыт использования бытовых кондиционеров показывает, что процесс охлаждения или
нагревания воздуха в помещении обладает некоторой инерционностью.
Например, после включения режима «холод» происходит нагнетание холодного воздуха, что
вызывает постепенное падение температуры, и даже в момент отключения этого режима
температура все же продолжает падать в течение небольшого отрезка времени.
Аналогичная ситуация наблюдается при включении и отключении режима «тепло». Поэтому
необходимо рассматривать в качестве параметров объекта управления не только температуру
воздуха в помещении, но и скорость изменения температуры.

29.

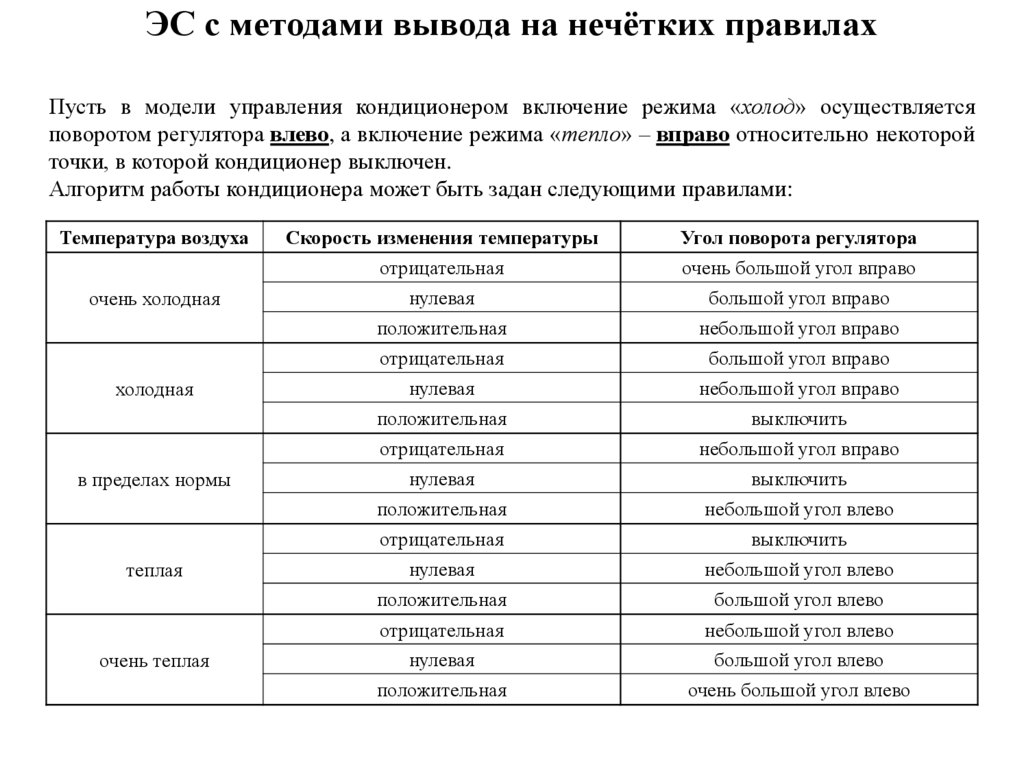
ЭС с методами вывода на нечётких правилах
Пусть в модели управления кондиционером включение режима «холод» осуществляется
поворотом регулятора влево, а включение режима «тепло» – вправо относительно некоторой
точки, в которой кондиционер выключен.
Алгоритм работы кондиционера может быть задан следующими правилами:
Температура воздуха
Скорость изменения температуры
Угол поворота регулятора
очень холодная
отрицательная
нулевая
очень большой угол вправо
большой угол вправо
положительная
небольшой угол вправо
отрицательная
нулевая
большой угол вправо
небольшой угол вправо
положительная
выключить
отрицательная
нулевая
небольшой угол вправо
выключить
положительная
небольшой угол влево
отрицательная
нулевая
выключить
небольшой угол влево
положительная
большой угол влево
отрицательная
нулевая
небольшой угол влево
большой угол влево
положительная
очень большой угол влево
холодная
в пределах нормы
теплая
очень теплая

30.

ЭС с методами вывода на нечётких правилах
Для того чтобы система могла обрабатывать эти правила, надо задать функции
принадлежности для нечетких подмножеств, определенных на значениях температуры
воздуха, скорости изменения температуры воздуха и угла поворота регулятора
кондиционера.
Пусть температура воздуха в комнате находится в пределах от 0°С до 40°С и включает
следующие градации:
- очень холодная (0-5°С)
- холодная (5-10°С)
- в пределах нормы (17-18°С)
- теплая (20-25°С)
- очень теплая (25-40°С).
В таком случае можно описать нечёткую переменную температура в следующем виде:
(deftemplate temperature
0 40 Celsius
(
(very_cold (0.0 1) (5 1) (6 0) )
(cold (4 0) (5 1) (10 1) (11 0) )
(normal (10 0) (17 1) (18 1) (20 0))
(warm (18 0) (20 1) (25 1) (26 0))
(very_warm (24 0) (25 1) (40 1))
)
)

31.

ЭС с методами вывода на нечётких правилах
Скорость изменения температуры можно описать следующим образом:
(deftemplate speed
-1 1 Grade_in_Minute
(
(negative (-1.0 1) (0 0) )
(zero (0.0 0) (0.0 1) (0.0 0) )
(positive (0 0) (1 1))
)
)
Данная нечёткая переменная включает три градации:
- отрицательная
- равная нулю
- положительная

32.

ЭС с методами вывода на нечётких правилах
В качестве выходной нечеткой переменной служит угол поворота регулятора кондиционера.
(deftemplate angle
-90 90 Grade
(
(very_big_angle_left (-90 1) (-45 1) (-44 0))
(big_angle_left (-46 0) (-45 1) (-20 1) (-19 0))
(little_angle_left (-21 0) (-20 1) (-0.1 1) (0 0))
(angle_zero (0 0) (0 1) (0 0))
(little_angle_right (0 0) (0.1 1) (20 1) (21 0))
(big_angle_right (19 0) (20 1) (45 1) (46 0))
(very_big_angle_right (44 0) (45 1) (90 1))
)
)
Данная нечёткая переменная может быть описана следующими подмножествами, заданными
на интервалах значений углов:
- очень большой угол влево (от -90° до -45°)
- большой угол влево (от -45° до -20°)
- небольшой угол влево (от -20° до 0.1°)
- выключить кондиционер (0°)
- небольшой угол вправо (от 0.1° до 20°)
- большой угол вправо (от 20° до 45°)
- очень большой угол вправо (от 45° до 90°)

33.

ЭС с методами вывода на нечётких правилах
Обеспечение функционирования алгоритма управления кондиционером будет описано в виде
15 правил, которые устанавливают нечёткое соответствие между лингвистическими
переменными temperature, speed и angle.
Рассмотрим первое правило:
(defrule Rule01
(declare (CF 0.9))
(temperature very_cold)
(speed negative)
=>
(assert (angle very_big_angle_right))
)
Оно читается следующим образом:
«Если температура воздуха в помещении очень холодная, а скорость изменения
температуры отрицательная, то следует включить режим «тепло», повернув регулятор
кондиционера на очень большой угол вправо».

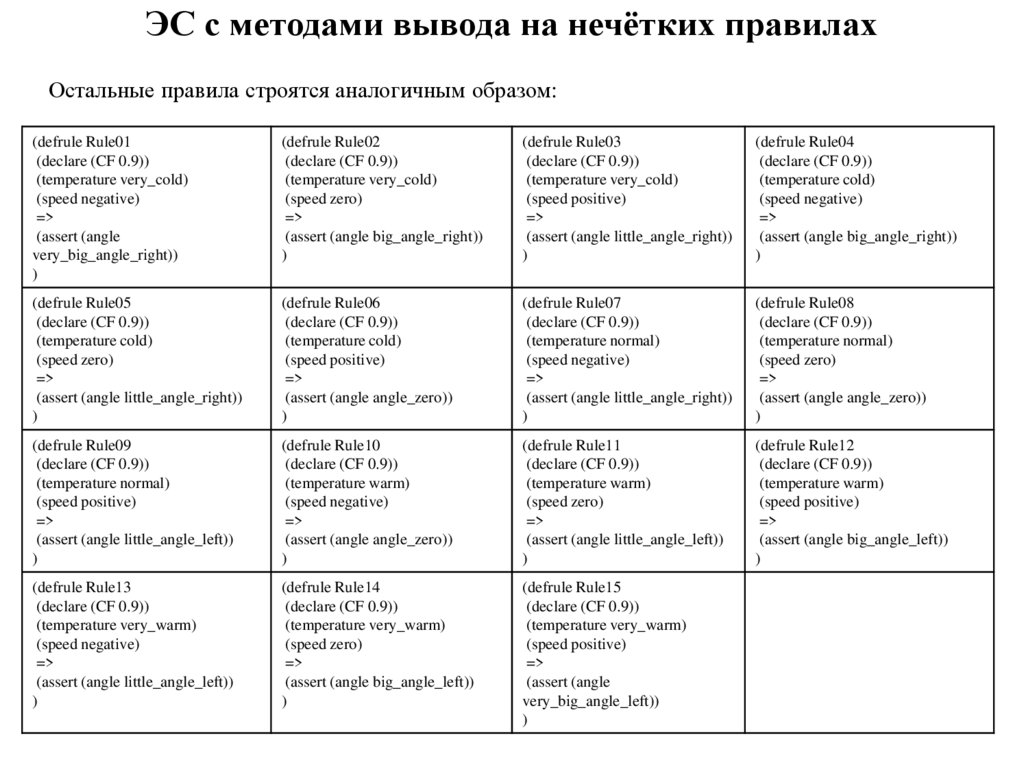
34.

ЭС с методами вывода на нечётких правилах
Остальные правила строятся аналогичным образом:
(defrule Rule01
(declare (CF 0.9))
(temperature very_cold)
(speed negative)
=>
(assert (angle
very_big_angle_right))
)
(defrule Rule02
(declare (CF 0.9))
(temperature very_cold)
(speed zero)
=>
(assert (angle big_angle_right))
)
(defrule Rule03
(declare (CF 0.9))
(temperature very_cold)
(speed positive)
=>
(assert (angle little_angle_right))
)
(defrule Rule04
(declare (CF 0.9))
(temperature cold)
(speed negative)
=>
(assert (angle big_angle_right))
)
(defrule Rule05
(declare (CF 0.9))
(temperature cold)
(speed zero)
=>
(assert (angle little_angle_right))
)
(defrule Rule06
(declare (CF 0.9))
(temperature cold)
(speed positive)
=>
(assert (angle angle_zero))
)
(defrule Rule07
(declare (CF 0.9))
(temperature normal)
(speed negative)
=>
(assert (angle little_angle_right))
)
(defrule Rule08
(declare (CF 0.9))
(temperature normal)
(speed zero)
=>
(assert (angle angle_zero))
)
(defrule Rule09
(declare (CF 0.9))
(temperature normal)
(speed positive)
=>
(assert (angle little_angle_left))
)
(defrule Rule10
(declare (CF 0.9))
(temperature warm)
(speed negative)
=>
(assert (angle angle_zero))
)
(defrule Rule11
(declare (CF 0.9))
(temperature warm)
(speed zero)
=>
(assert (angle little_angle_left))
)
(defrule Rule12
(declare (CF 0.9))
(temperature warm)
(speed positive)
=>
(assert (angle big_angle_left))
)
(defrule Rule13
(declare (CF 0.9))
(temperature very_warm)
(speed negative)
=>
(assert (angle little_angle_left))
)
(defrule Rule14
(declare (CF 0.9))
(temperature very_warm)
(speed zero)
=>
(assert (angle big_angle_left))
)
(defrule Rule15
(declare (CF 0.9))
(temperature very_warm)
(speed positive)
=>
(assert (angle
very_big_angle_left))
)

35.

ЭС с методами вывода на нечётких правилах
Однако в первую очередь необходимо создать правило, которое будет уточнять данные
температуры и скорости изменения температуры у пользователя:
(defrule start
(initial-fact)
=>
(set-fuzzy-inference-type max-prod)
;(set-fuzzy-inference-type max-min)
(printout t crlf "===> Введите температуру воздуха в помещении: ")
(bind ?t (read))
(assert (temperature (pi 0 ?t)))
(printout t crlf "===> Введите скорость изменени9 температуры (от -1 до 1) : ")
(bind ?s (read))
(assert (speed (?s 0) (?s 1) (?s 0)))
)
Примечание.
Команда set-fuzzy-inference-type устанавливает используемый механизм логического вывода
для модификации нечёткого множества.

36.

ЭС с методами вывода на нечётких правилах
Особо хотелось бы обратить внимание на добавление в систему факта с текущим значением
температуры вида:
(temperature (pi 0 ?t)))
Все дело в том, что temperature является лингвистической переменной и ее первичными
фактами должны являться нечеткие множества. Иными словами значения переменной
temperature должны иметь тип FUZZY.
При этом конструкция вида (temperature 22) недопустима. Поэтому четкое значение терма 22
надо представить нечеткой величиной, например,
(temperature (pi 0 22))
или, что тоже самое,
(temperature (22 0) (22 1) (22 0))
Аналогичная ситуация с лингвистической переменной speed.

37.

ЭС с методами вывода на нечётких правилах
Заключительное правило ShowResults служит для вывода результатов и имеет самый низкий
приоритет, что позволяет ему включиться в работу только после согласования всех остальных
правил.
После запуска программы в работу, именно это правило формирует вид информации, которая
выдается на экран компьютера:
(defrule ShowResults
(declare (salience -1))
?ang <- (angle ?)
=>
(bind ?f (moment-defuzzify ?ang))
(printout t "Угол поворота регулятора кондиционера: " ?f crlf)
)
Примечание. Функция moment-defuzzify позволяет получить чёткую величину из нечёткого
множества (дефаззификация).

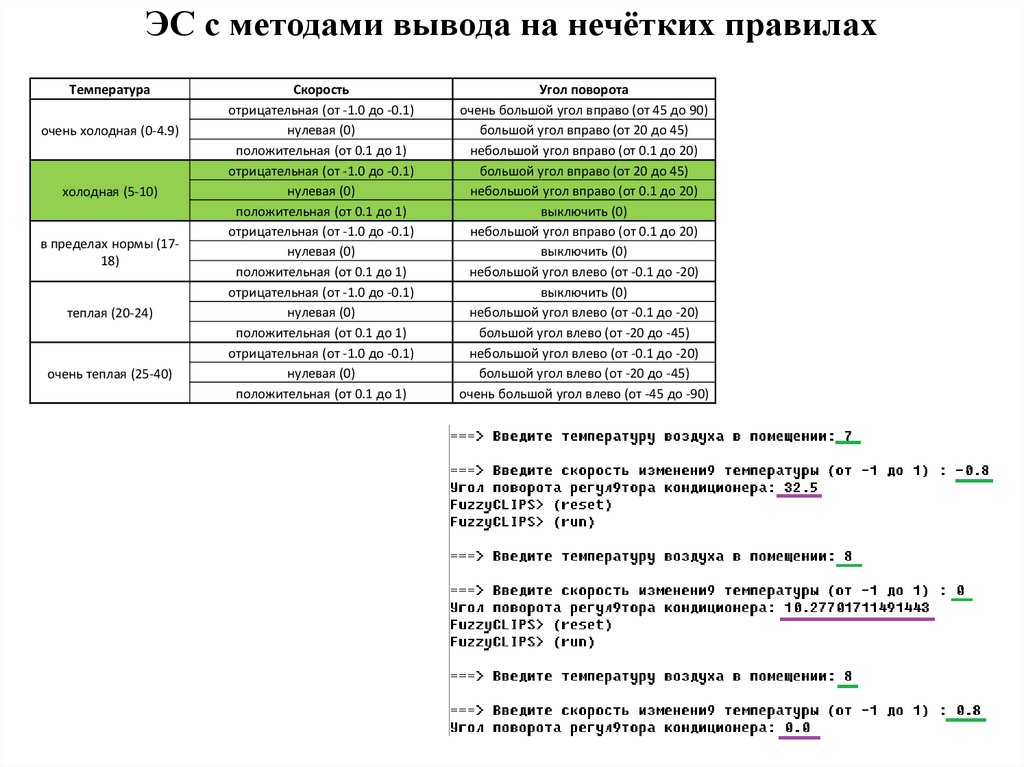
38.

ЭС с методами вывода на нечётких правилах
Температура
очень холодная (0-4.9)
холодная (5-10)
в пределах нормы (1718)
теплая (20-24)
очень теплая (25-40)
Скорость
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
Угол поворота
очень большой угол вправо (от 45 до 90)
большой угол вправо (от 20 до 45)
небольшой угол вправо (от 0.1 до 20)
большой угол вправо (от 20 до 45)
небольшой угол вправо (от 0.1 до 20)
выключить (0)
небольшой угол вправо (от 0.1 до 20)
выключить (0)
небольшой угол влево (от -0.1 до -20)
выключить (0)
небольшой угол влево (от -0.1 до -20)
большой угол влево (от -20 до -45)
небольшой угол влево (от -0.1 до -20)
большой угол влево (от -20 до -45)
очень большой угол влево (от -45 до -90)

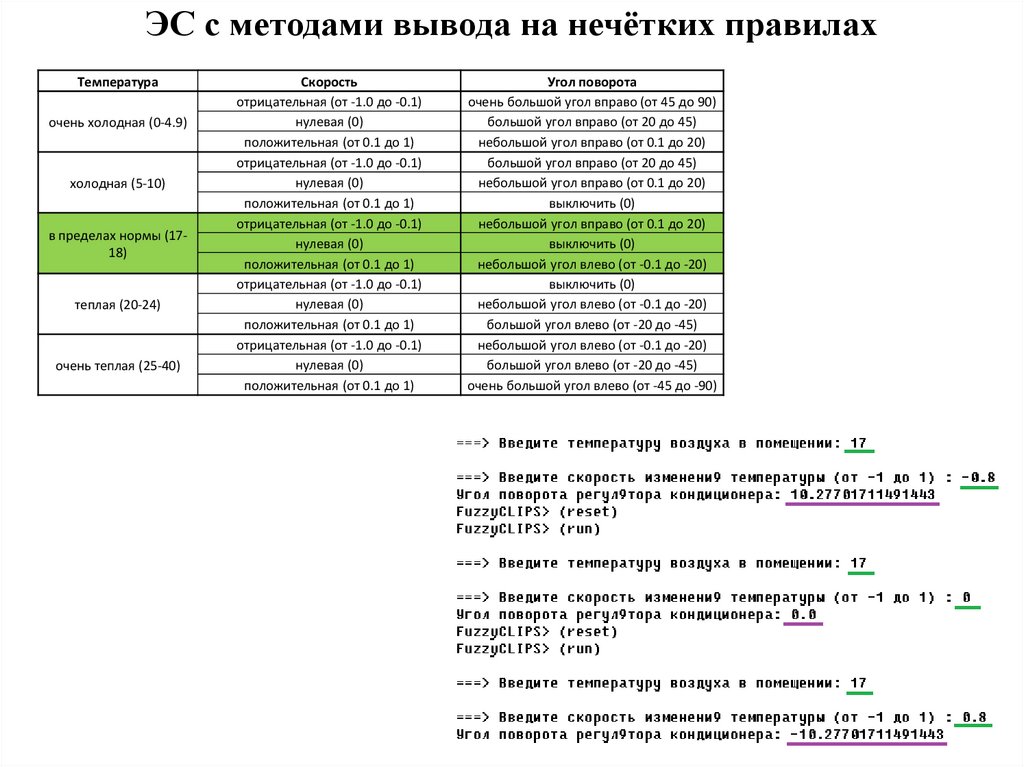
39.

ЭС с методами вывода на нечётких правилах
Температура
очень холодная (0-4.9)
холодная (5-10)
в пределах нормы (1718)
теплая (20-24)
очень теплая (25-40)
Скорость
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
Угол поворота
очень большой угол вправо (от 45 до 90)
большой угол вправо (от 20 до 45)
небольшой угол вправо (от 0.1 до 20)
большой угол вправо (от 20 до 45)
небольшой угол вправо (от 0.1 до 20)
выключить (0)
небольшой угол вправо (от 0.1 до 20)
выключить (0)
небольшой угол влево (от -0.1 до -20)
выключить (0)
небольшой угол влево (от -0.1 до -20)
большой угол влево (от -20 до -45)
небольшой угол влево (от -0.1 до -20)
большой угол влево (от -20 до -45)
очень большой угол влево (от -45 до -90)

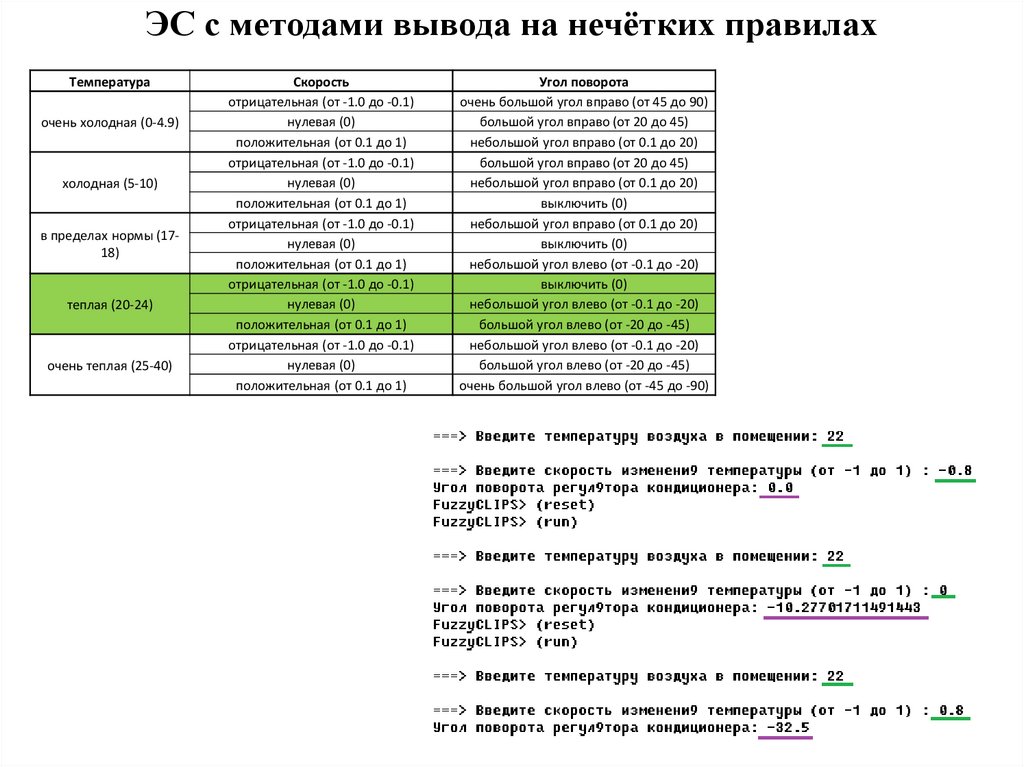
40.

ЭС с методами вывода на нечётких правилах
Температура
очень холодная (0-4.9)
холодная (5-10)
в пределах нормы (1718)
теплая (20-24)
очень теплая (25-40)
Скорость
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
Угол поворота
очень большой угол вправо (от 45 до 90)
большой угол вправо (от 20 до 45)
небольшой угол вправо (от 0.1 до 20)
большой угол вправо (от 20 до 45)
небольшой угол вправо (от 0.1 до 20)
выключить (0)
небольшой угол вправо (от 0.1 до 20)
выключить (0)
небольшой угол влево (от -0.1 до -20)
выключить (0)
небольшой угол влево (от -0.1 до -20)
большой угол влево (от -20 до -45)
небольшой угол влево (от -0.1 до -20)
большой угол влево (от -20 до -45)
очень большой угол влево (от -45 до -90)

41.

ЭС с методами вывода на нечётких правилах
Температура
очень холодная (0-4.9)
холодная (5-10)
в пределах нормы (1718)
теплая (20-24)
очень теплая (25-40)
Скорость
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
Угол поворота
очень большой угол вправо (от 45 до 90)
большой угол вправо (от 20 до 45)
небольшой угол вправо (от 0.1 до 20)
большой угол вправо (от 20 до 45)
небольшой угол вправо (от 0.1 до 20)
выключить (0)
небольшой угол вправо (от 0.1 до 20)
выключить (0)
небольшой угол влево (от -0.1 до -20)
выключить (0)
небольшой угол влево (от -0.1 до -20)
большой угол влево (от -20 до -45)
небольшой угол влево (от -0.1 до -20)
большой угол влево (от -20 до -45)
очень большой угол влево (от -45 до -90)

42.

ЭС с методами вывода на нечётких правилах
Температура
очень холодная (0-4.9)
холодная (5-10)
в пределах нормы (1718)
теплая (20-24)
очень теплая (25-40)
Скорость
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
отрицательная (от -1.0 до -0.1)
нулевая (0)
положительная (от 0.1 до 1)
Угол поворота
очень большой угол вправо (от 45 до 90)
большой угол вправо (от 20 до 45)
небольшой угол вправо (от 0.1 до 20)
большой угол вправо (от 20 до 45)
небольшой угол вправо (от 0.1 до 20)
выключить (0)
небольшой угол вправо (от 0.1 до 20)
выключить (0)
небольшой угол влево (от -0.1 до -20)
выключить (0)
небольшой угол влево (от -0.1 до -20)
большой угол влево (от -20 до -45)
небольшой угол влево (от -0.1 до -20)
большой угол влево (от -20 до -45)
очень большой угол влево (от -45 до -90)