Метрология. Правила написания обозначения единиц. Основные погятия теории погрешностей

1. Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Башкирский

государственный университет»
Лекция №2
МЕТРОЛОГИЯ.
ПРАВИЛА НАПИСАНИЯ ОБОЗНАЧЕНИЯ ЕДИНИЦ.
ОСНОВНЫЕ ПОГЯТИЯ ТЕОРИИ ПОГРЕШНОСТЕЙ
Метрология

2.

ПРАВИЛА НАПИСАНИЯ ОБОЗНАЧЕНИЯ ЕДИНИЦ
Существует определенный формализм написания обозначений единиц, который
помимо Постановления Правительства излагается в разделе 8 ГОСТ 8.417-2002 (с
поправками от 2019 г.). Основные моменты этого формализма следующие:
При написании значений величин применяют обозначения единиц буквами или
специальными знаками (…°, …ʹ, …ʺ), причем устанавливают два вида буквенных
обозначений: международное (с использованием букв латинского или греческого
алфавита) и русское (с использованием букв русского алфавита).
Буквенные обозначения единиц печатают прямым шрифтом. В обозначениях
единиц точку как знак сокращения не ставят.
Обозначения единиц помещают за числовыми значениями величин и в строку с
ними (без переноса на следующую строку). Числовое значение, представляющее
собой с косой чертой, стоящее перед обозначением единицы, заключают в скобки.
Метрология

3.

ПРАВИЛА НАПИСАНИЯ ОБОЗНАЧЕНИЯ ЕДИНИЦ
Между последней цифрой числа и обозначением единицы
оставляют пробел.
Правильно:
Неправильно:
100 kW; 100 кВт
100kW; 100кВт
80 %
80%
20 °С
20°С
(1/60) s-1
1/60s-1
Исключения составляют обозначения в виде знака,
поднятого над строкой, впереди которого пробел не
оставляют.
Правильно:
Неправильно:
20°
20 °
Метрология

4.

ПРАВИЛА НАПИСАНИЯ ОБОЗНАЧЕНИЯ ЕДИНИЦ
При наличии десятичной дроби в числовом значении
величины обозначение единицы помещают за всеми цифрами.
Правильно:
Неправильно:
423,06 m; 423,06 м
423 m 0,6; 423 м, 06
5,758° или 5°45,48´
5°758 или 5°45´,48
или 5°45´28,8ʺ
или 5°45´28ʺ,8
Метрология

5.

ПРАВИЛА НАПИСАНИЯ ОБОЗНАЧЕНИЯ ЕДИНИЦ
При
указании
значений
величин
с
предельными
отклонениями числовые значения с предельными отклонениями
заключают в скобки и обозначения единиц помещают за
скобками или проставляют обозначение единицы за числовым
значением величины и за ее предельным отклонением.
Правильно:
Неправильно:
(100,0 ± 0,1) kg
100,0±0,1 kg
50 g ± 1 g; 50 г ± 1 г
50 ±1 g; 50 ±1 г
Метрология

6.

ПРАВИЛА НАПИСАНИЯ ОБОЗНАЧЕНИЯ ЕДИНИЦ
Если в тексте приведен ряд числовых значений величины,
который выражен одной и той же единицей величины, то
обозначение единицы величины указывают только после
последнего числового значения.
Пример – 1,0; 1,5; 2,0; 2,5 мм
Метрология

7.

ПРАВИЛА НАПИСАНИЯ ОБОЗНАЧЕНИЯ ЕДИНИЦ
Интервалы чисел в тексте записывают со словами «от» «до» (имея в
виду: «от+
до+ включительно»), если после чисел указана единица
величины, или через тире, если эти числа являются безразмерными
коэффициентами.
Если в тексте стандарта приводят диапазон числовых значений
величины, который выражен одной и той же единицей величины, то
обозначение единицы величины указывается за последним числовым
значением диапазона, за исключением знаков «%», «°С», «+°».
Примеры
1… от 10 до 100 кг.
2… от 65 % до 70 %.
3.. от 10 °С до 20 °С.
Метрология

8.

ПРАВИЛА НАПИСАНИЯ ОБОЗНАЧЕНИЯ ЕДИНИЦ
Если интервал чисел охватывает порядковые
номера, то для записи интервала используют тире.
Пример - … рисунки 1-14.
Недопустимо отделять единицу величины от
числового значения (разносить их на разные строки
или страницы), кроме единиц величин, помещаемых
в таблицах …».
Метрология

9. Что характеризует погрешность?

технический манометр
МТ-100
9
Метрология

10. ПОГРЕШНОСТЬ

Истинное значение ФВ
Результат измерения (РИ)
Действительное значение ФВ
Погрешность результата измерения – это отклонение
результата измерения X от истинного (или действительного)
значения Q измеряемой величины:
∆X = X -Q.
10
Метрология

11.

Погрешность средства измерений – разность между
показанием СИ и истинным (действительным) значением
измеряемой ФВ. Она характеризует точность средства
измерений (характеристику качества СИ, отражающую близость
его погрешности к нулю). Понятия погрешности результата
измерения и погрешности средства измерений во многом
близки друг к другу и классифицируются по одинаковым
признакам.
11
Метрология

12.

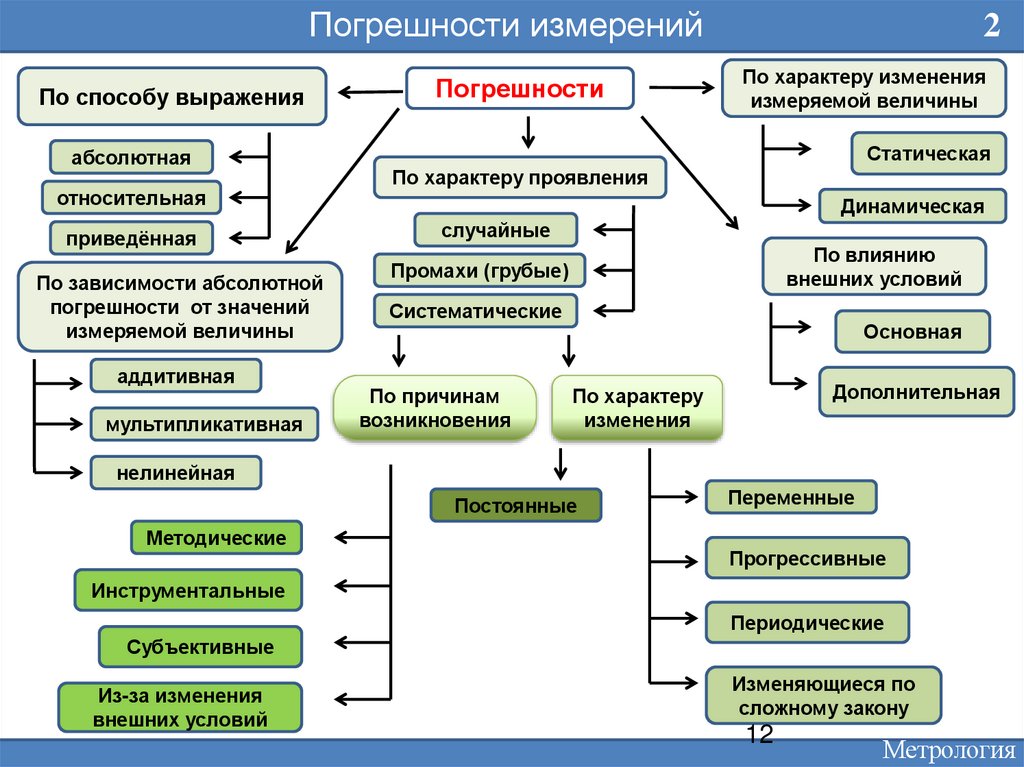
Погрешности измерений
По способу выражения
абсолютная
относительная
приведённая
По зависимости абсолютной
погрешности от значений
измеряемой величины
аддитивная
мультипликативная
Погрешности
2
По характеру изменения
измеряемой величины
Статическая
По характеру проявления
Динамическая
случайные
По влиянию
внешних условий
Промахи (грубые)
Систематические
По причинам
возникновения
Основная
Дополнительная
По характеру
изменения
нелинейная
Постоянные
Методические
Переменные
Прогрессивные
Инструментальные
Периодические
Субъективные
Из-за изменения
внешних условий
Изменяющиеся по
сложному закону
12
Метрология

13. ПО ХАРАКТЕРУ ПОЯВЛЕНИЯ

СЛУЧАЙНЫЕ ПОГРЕШНОСТИ
СИСТЕМАТИЧЕСКИЕ ПОГРЕШНОСТИ
ПРОМАХИ (ГРУБЫЕ
ПОГРЕШНОСТИ)
Рис. 2.1. Изменение: а – случайной, б – постоянной и переменной
систематических погрешностей от измерения к измерению.
13
Метрология

14. ПО ХАРАКТЕРУ ПОЯВЛЕНИЯ

СЛУЧАЙНЫЕ ПОГРЕШНОСТИ
СИСТЕМАТИЧЕСКИЕ ПОГРЕШНОСТИ
№
1
2
4
5
6
I, А
3,1
3,2
3,2
3,1
3,4
№
1
2
4
5
6
I, А
3,8
3,7
3,6
3,5
3,4
№
1
2
4
5
6
R, Ом
150
151
152
153
154
№
1
2
4
5
6
R, Ом
150
151
150
159
152
ПРОМАХИ (ГРУБЫЕ
ПОГРЕШНОСТИ)
14
Метрология

15. ПО СПОСОБУ ВЫРАЖЕНИЯ

абсолютные
∆X = X– Q
приведённые
относительные
Абсолютная погрешность
выражается в единицах
измеряемой величины.
Δx = 0,05 м при x = 100 м,
Δx = 0,05 м при x = 1 м
при x = 0
δ→∞
15
Метрология

16.

Погрешности измерений
По способу выражения
абсолютная
относительная
приведённая
По зависимости абсолютной
погрешности от значений
измеряемой величины
аддитивная
мультипликативная
Погрешности
2
По характеру изменения
измеряемой величины
Статическая
По характеру проявления
Динамическая
случайные
По влиянию
внешних условий
Промахи (грубые)
Систематические
По причинам
возникновения
Основная
Дополнительная
По характеру
изменения
нелинейная
Постоянные
Методические
Переменные
Прогрессивные
Инструментальные
Периодические
Субъективные
Из-за изменения
внешних условий
Изменяющиеся по
сложному закону
16
Метрология

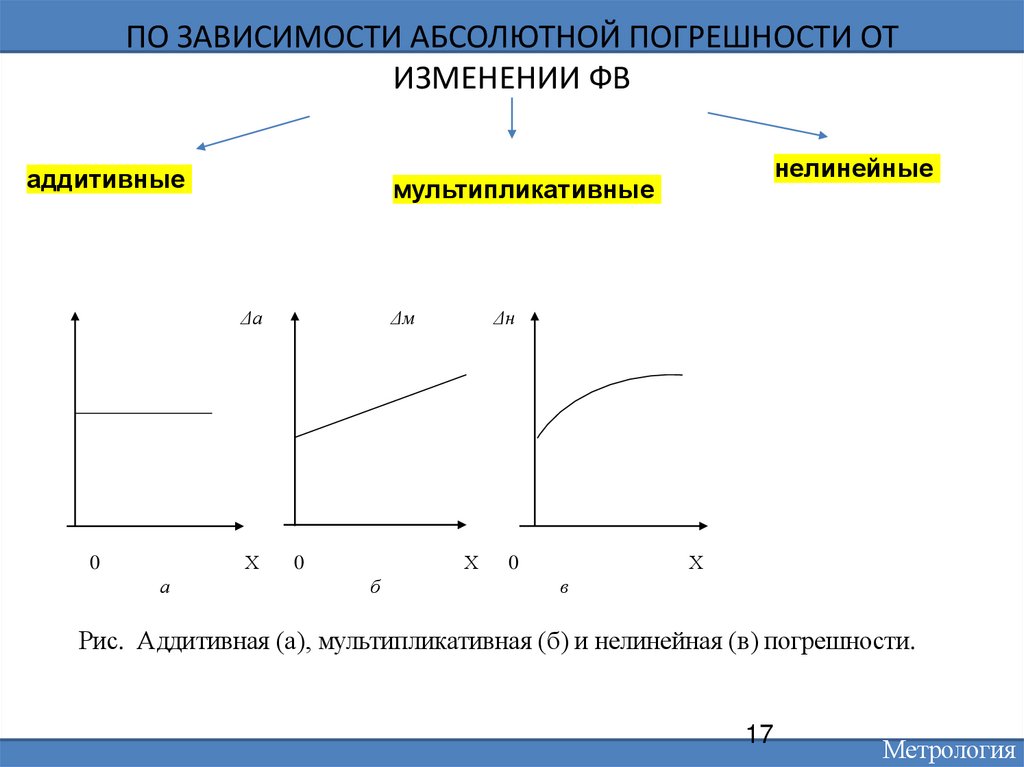
17. ПО ЗАВИСИМОСТИ АБСОЛЮТНОЙ ПОГРЕШНОСТИ ОТ ИЗМЕНЕНИИ ФВ

аддитивные
Δa
Х
0
а
нелинейные
мультипликативные
Δм
Δн
Х
0
б
Х
0
в
Рис. Аддитивная (а), мультипликативная (б) и нелинейная (в) погрешности.
17
Метрология

18. ПО ВЛИЯНИЮ ВНЕШНИХ УСЛОВИЙ

ОСНОВНАЯ
Основная погрешность
средства измерений –
погрешность
СИ,
применяемого
в
нормальных условиях.
Для каждого средства
оговариваются условия
эксплуатации,
при
которых
нормируется
его погрешность.
ДОПОЛНИТЕЛЬНАЯ
Дополнительная
погрешность
средства
измерений
–
составляющая погрешности СИ,
возникающая
дополнительно
к
основной погрешности, вследствие
отклонения какой-либо из влияющих
величин от нормального ее значения
или вследствие ее выхода за пределы
нормальной области значений.
18
Метрология

19.

19
Метрология

20. ПО ЗАВИСИМОСТИ ОТ ВЛИЯНИЯ ХАРАКТЕРА ИЗМЕНЕНИЯ ИЗМЕРЯЕМЫХ ВЕЛИЧИН

ДИНАМИЧЕСКАЯ
СТАТИЧЕСКАЯ
Статической называется
погрешность
средства
измерений,
применяемого
для
измерения
ФВ,
принимаемой
за
неизменную.
Динамической
называется
погрешность СИ, возникающая
дополнительно при измерении
изменяющейся
(в
процессе
измерений) ФВ. Динамическая
погрешность СИ обусловлена
несоответствием его реакции на
скорость (частоту) изменения
измеряемого
сигнала.
Пример статической погрешности – погрешность, возникающая при измерении
длины земельного участка. Динамическая погрешность возникает при измерении
изменения концентрации во времени или скорости.
20
Метрология

21.

Погрешности измерений
По способу выражения
абсолютная
относительная
приведённая
По зависимости абсолютной
погрешности от значений
измеряемой величины
аддитивная
мультипликативная
2
По характеру изменения
измеряемой величины
Погрешности
Статическая
По характеру проявления
Динамическая
случайные
По влиянию
внешних условий
Промахи (грубые)
Систематические
По причинам
возникновения
Основная
Дополнительная
По характеру
изменения
нелинейная
Постоянные
Методические
Переменные
Прогрессивные
Инструментальные
Периодические
Субъективные
Из-за изменения
внешних условий
Изменяющиеся по
сложному закону
21
Метрология

22.

СИСТЕМАТИЧЕСКАЯ ПОГРЕШНОСТЬ
Систематическая погрешность представляет собой определенную функцию
влияющих факторов, состав которых зависит от физических, конструктивных и
технологических особенностей СИ, условий их применения, а также от
индивидуальных качеств наблюдателя. В метрологической практике при оценке
систематических погрешностей должно учитываться влияние следующих основных
составляющих процесса измерения:
1. Объект измерения – перед измерением он должен быть достаточно хорошо
изучен с целью корректного выбора его модели. Чем полнее модель соответствует
объекту, тем точнее могут быть получены результаты измерения.
2. Субъект измерения – его вклад в погрешность измерения необходимо уменьшать
путем подбора операторов высокой квалификации и соблюдения требований
эргономики при разработке СИ.
3. Метод и средство измерений – их правильный выбор чрезвычайно важен и
производится на основе априорной информации об объекте измерения. Чем больше
априорной информации, тем точнее может быть проведено измерение. Основной
вклад в систематическую погрешность вносит, как правило, методическая
погрешность.
4. Условия измерения – обеспечение и стабилизация нормальных условий являются
необходимыми требованиями для минимизации дополнительной погрешности,
которая по своей природе, как правило, является систематической.
22
Метрология

23.

Погрешности
Систематические
По причинам
возникновения
По характеру
изменения
Постоянные
Методические
Переменные
Прогрессивные
Инструментальные
Периодические
Субъективные
Из-за изменения
внешних условий
Изменяющиеся по
сложному закону
23
Метрология

24.

ПО ХАРАКТЕРУ ИЗМЕНЕНИЯ
Постоянные погрешности – погрешности, которые длительное время
сохраняют свое значение, например, в течение времени выполнения всего
ряда измерений. Они встречаются наиболее часто. К постоянным относятся
погрешности большинства мер (гирь, концевых мер длины), погрешности
градуировки шкал измерительных приборов, погрешность от постоянного
дополнительного веса на чашке весов и др.
Прогрессивные
(ДРЕЙФОВАЯ)
погрешности
–
непрерывно
возрастающие или убывающие погрешности. К ним относятся, например,
погрешности
вследствие
износа
измерительных
наконечников,
контактирующих с деталью при контроле ее прибором активного контроля,
постепенный разряд батареи, питающей СИ и др.
Периодические погрешности – погрешности, значение которых является
периодической
функцией
времени
или
перемещения
указателя
измерительного прибора. Обычно эти погрешности встречаются в
угломерных приборах с круговой шкалой. Также примером может служить
погрешность, обусловленная суточными колебаниями напряжения силовой
питающей сети, температуры окружающей среды и др.
Погрешности, изменяющиеся по сложному закону, происходят
вследствие совместного действия нескольких систематических погрешностей.
24
Метрология

25.

ПО ПРИЧИНАМ ВОЗНИКНОВЕНИЯ
25
Метрология

26.

26
Метрология

27.

СПОСОБЫ ОБНАРУЖЕНИЯ И УСТРАНЕНИЯ СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Результаты
наблюдений,
полученные
при
наличии
систематической
погрешности, называются неисправленными. При проведении измерений стараются
в
максимальной
степени исключить
или учесть
влияние
систематических
погрешностей. Это может быть достигнуто следующими путями:
Устранение источников погрешностей до начала измерений. В большинстве
областей измерений известны главные источники систематических погрешностей и
разработаны методы, исключающие их возникновение или устраняющие их влияние
на результат измерения. В связи с этим в практике измерений стараются устранить
систематические погрешности не путем обработки экспериментальных данных, а
применением СИ, реализующих соответствующие методы измерений;
Определением поправок и внесением их в результат измерения;
Оценкой границ неисключенных систематических погрешностей.
27
Метрология

28.

28
Метрология

29.

Для устранения постоянных систематических погрешностей применяют следующие методы:
Метод измерений замещением, являющийся разновидностью метода
сравнения с мерой. Сравнение осуществляется замещением измеряемой величины
мерой с известным значением величины, причем так, что при этом в состоянии и
действии всех используемых СИ не происходит никаких изменений.
Пример: при измерении электрических параметров, таких как: сопротивление,
емкость, индуктивность, объект подключается в измерительную цепь. В
большинстве случаев при этом пользуются нулевыми методами (мостовым,
компенсационным и др.), при которых производится электрическое
уравновешивание цепи. После этого, не меняя схемы, вместо измеряемого объекта
включают меру переменного значения (магазин сопротивлений, емкости,
индуктивности и т.д.) и, изменяя их значение, добиваются восстановления
равновесия цепи. В этом случае способом замещения исключается остаточная
неуравновешенность мостовых цепей, влияния на цепь магнитных и
электрических полей и др.
Пример: взвешивание на пружинных весах, у которых имеется постоянная
систематическая погрешность (из-за смещения шкалы, например). Взвешивание
производится в два приема (рис. 3.1).
29
Метрология

30.

Рис. 3.1 Иллюстрация метода измерений замещением (метод Борда).
Вначале на чашу весов помещают взвешиваемое тело массой mх и отмечают
положение указателя (на отметке N). Затем взвешиваемое тело замещают гирями
такой массы m0 , чтобы вновь добиться прежнего отклонения указателя N. Очевидно,
что при одинаковых отклонениях указателя будет выполняться условие mх =m0, и
систематическая погрешность весов не скажется на результате взвешивания. Такой
способ взвешивания с поочередным помещением измеряемой массы и гирь на одну и
ту же чашку весов называется методом Борда.
30
Метрология

31.

Рис. 3.2 Иллюстрация метода
противопоставления.
31
Метрология

32.

32
Метрология

33.

Метод рандомизации – наиболее универсальный способ
исключения неизвестных постоянных систематических
погрешностей. Суть его состоит в том, что одна и та же
величина измеряется различными методами (приборами).
Систематические погрешности каждого из них для всей
совокупности являются разными случайными величинами.
Вследствие этого, при увеличении числа используемых
методов (приборов) систематические погрешности взаимно
компенсируются.
33
Метрология

34.

Для устранения переменных и монотонно изменяющихся
систематических
погрешностей
применяют
следующие
приемы и методы.
Анализ
знаков
неисправленных
случайных
погрешностей. Если знаки неисправленных случайных
погрешностей чередуются с какой-либо закономерностью, то
наблюдается переменная систематическая погрешность. Если
последовательность знаков «+» у случайных погрешностей
сменяется последовательностью знаков «-», или наоборот, то
присутствует монотонно изменяющаяся систематическая
погрешность. Если группы знаков «+» и «-» у случайных
погрешностей чередуются, то присутствует периодическая
систематическая погрешность.
34
Метрология

35.

Графический метод – один из наиболее простых способов обнаружения
переменной
систематической
Заключается
он
неисправленных
в
погрешности
графическом
значений
результатов
в
результатах
представлении
наблюдений.
наблюдений.
последовательности
На
графике
через
построенные точки проводят плавную кривую, которая выражает тенденцию в
изменении результата измерения, если она существует. Если тенденция не
наблюдается,
то
переменную
систематическую
погрешность
считают
практически отсутствующей.
Пример: частым случаем погрешности, изменяющейся по определенному
закону,
является
погрешность,
прогрессирующая
по
линейному
закону,
например, пропорционально времени. В этом случае погрешность можно
оценить и исключить следующим образом. Если известно, что при измерении
постоянной величины х0 систематическая погрешность изменяется линейно во
времени, т.е. хизм = х0 + C∙t (где C = const), то для ее исключения достаточно
сделать два наблюдения х1 и х2 с фиксацией времени t1 и t2 (рис. 3.3).
35
Тогда искомое значение величины будет
Метрология

36.

x
t2
X2
x1
X0
t1
t
Рис. 3.3. Линейное изменение систематической погрешности
36
Метрология

37.

Если
предположение
о
линейном
законе
изменения
систематической
погрешности не очевидно, то для контроля систематической погрешности применяют
метод симметричных наблюдений.
Метод
симметричных
наблюдений.
Применяется
для
исключения
прогрессирующего влияния какого-либо фактора, являющегося линейной функцией
времени (например, постепенного прогрева аппаратуры, падения напряжения в цепи
питания, вызванного разрядом аккумулятора и т.д.). Такая функция может быть
изображена в виде графика, на котором по оси абсцисс отложено время, а по оси
ординат
–
прогрессивная
погрешность.
Способ
симметричных
наблюдений
заключается в том, что в течение некоторого интервала времени выполняется
несколько измерений одной и той же величины постоянного размера и за
окончательный
результат
принимается
полусумма
отдельных
результатов,
симметричных по времени относительно середины интервала. Рекомендуется
использовать данный способ, когда не очевидна возможность существования
прогрессивной погрешности.
37
Метрология

38.

x
x5
x4
x3
x2
x1
t1
t2
t3
t4
t5
t
Рис. Метод симметричных наблюдений
38
Метрология

39.

Исключение
систематических
погрешностей
путем
введения
поправок. В ряде случаев систематические погрешности могут быть
вычислены и исключены из результата измерения. Для этого используются
поправки. Поправка Cj – значение величины, одноименной с измеряемой,
которое вводится в результат измерения с целью исключения составляющих
систематической погрешности Θj. При Cj=-Θj – j-я составляющая
систематической погрешности полностью устраняется из результата
измерения. Поправки определяются экспериментально или в результате
специальных теоретических исследований и задаются в виде таблиц,
графиков или формул.
Введением одной поправки устраняется влияние только одной
составляющей систематической погрешности. Для устранения всех
составляющих в результат измерения приходится вводить множество
поправок. При этом вследствие ограниченной точности определения
поправок случайные погрешности результата измерения39накапливаются и
Метрология

40.

ПРАВИЛА ОКРУГЛЕНИЯ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Эмпирически были установлены следующие правила округления рассчитанного
значения погрешности и полученного результата измерения.
1.
Погрешность результата измерения указывается двумя значащими цифрами, если
первая из них равна 1 или 2, и одной – если первая есть 3 или более.
2.
Результат измерения округляется до того же десятичного знака, которым
оканчивается округленное значение абсолютной погрешности. Если десятичная
дробь в числовом значении результата измерений оканчивается нулями, то нули
отбрасываются до того разряда, который соответствует разряду числового значения
погрешности.
Пример: Число 999,99872142 при погрешности ±0,000005 следует округлять до
999,998721.
3. Если цифра старшего из отбрасываемых разрядов меньше 5, то остальные
цифры числа не изменяются. Лишние цифры в целых числах заменяются нулями, а в
десятичных дробях отбрасываются. Пример: При сохранении четырех значащих цифр
число 283435 должно быть округлено до 283400; число 384,435 – до 384,4.
40
Метрология

41.

ПРАВИЛА ОКРУГЛЕНИЯ РЕЗУЛЬТАТОВ ИЗМЕНЕНИЙ
4. Если цифра старшего отбрасываемого разряда больше или равна 5, но за ней
следуют отличные от нуля цифры, то последнюю оставляемую цифру увеличивают на
единицу.
Пример: При сохранении трех значащих цифр число 17,58 округляют до 17,6;
число 18598 – до 18600; число 352,521 – 353.
5. Если отбрасываемая цифра равна 5, а следующие за ней цифры неизвестны или
являются нулями, то последнюю сохраняемую цифру числа не изменяют, если она
четная, и увеличивают на единицу, если она нечетная.
Пример: При сохранении трех значащих цифр число 264,50 округляют до 264;
число 645,5 – до 646.
6. Округление производится лишь в окончательном ответе, а все предварительные
вычисления проводят с одним-двумя лишними знаками. Если руководствоваться этими
правилами округления, то количество значащих цифр в числовом значении результата
измерений позволяет ориентировочно судить о точности измерения. Это связано с тем,
что предельная погрешность, обусловленная округлением, равна половине единицы
последнего разряда числового значения результата измерения.
41
Метрология