Основные понятия теории погрешностей

1.

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ
ФГБОУ ВО «ЮГОРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Высшая нефтяная школа
Метрологические основы химического анализа
«ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ОГРЕШНОСТЕЙ»
старший преподаватель Смородинова Т.Н.
[email protected]

2.

Классификация погрешностей
Значение измеряемой ФВ и результат измерения:
- Истинное
- Действительное
Погрешность результата измерения – это отклонение результата
измерения X
от истинного (или действительного) значения Q
измеряемой величины.
2

3.

Классификация
погрешностей
3

4.

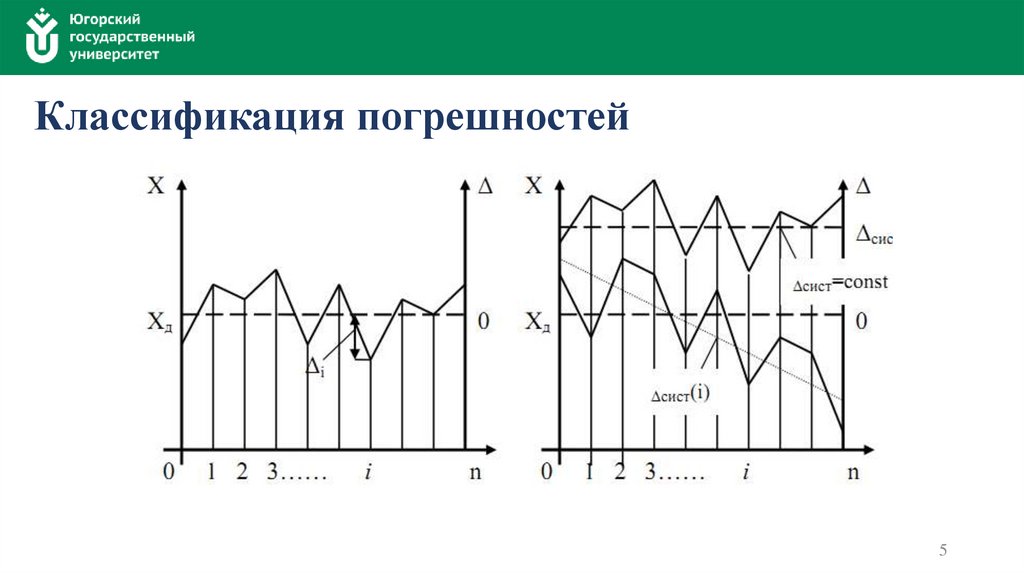
Классификация погрешностей
По характеру проявления погрешности делятся на случайные, систематические,
прогрессирующие и промахи, или грубые погрешности.
Случайная погрешность – составляющая погрешности измерения, изменяющаяся
случайным образом (по знаку и значению) в серии повторных измерений одного и того
же размера ФВ, проведенных с одинаковой тщательностью в одних и тех же условиях.
Систематическая погрешность – составляющая погрешности измерения, остающаяся
постоянной или закономерно меняющаяся при повторных измерениях одной и той же ФВ.
Прогрессирующая (дрейфовая) погрешность – это непредсказуемая погрешность,
медленно меняющаяся во времени.
Грубая погрешность (промах) – это случайная погрешность результата отдельного
наблюдения, входящего в ряд измерений; для данных условий она резко отличается от
остальных результатов этого ряда.
4

5.

Классификация погрешностей
5

6.

Классификация погрешностей
По способу выражения различают абсолютную, относительную и
приведенную погрешности.
Абсолютная погрешность - разница между результатом измерения X и
истинным значением Q измеряемой величины.
Относительная погрешность - отношение абсолютной погрешности
измерения к действительному или измеренному значению измеряемой
величины.
Приведенная погрешность средства измерений – это относительная
погрешность, в которой абсолютная погрешность СИ отнесена к
условно принятому значению N x , постоянному во всем диапазоне
6
измерений или его части.

7.

Классификация погрешностей
Абсолютная погрешность
Относительная погрешность
Приведенная погрешность
7

8.

Классификация погрешностей
В зависимости от причин возникновения различают инструментальные погрешности
измерения, погрешности метода измерений, погрешности из-за изменения условий измерения
и субъективные погрешности измерения.
Инструментальная погрешность измерения обусловлена погрешностью применяемого
средства измерения.
Погрешность метода измерений – составляющая систематической погрешности
измерений из-за несовершенства принятого метода измерений.
Погрешность (измерения) из-за изменения условий измерения – это составляющая
систематической погрешности измерения, являющаяся следствием неучтенного влияния
отклонения в одну сторону какого-либо из параметров, характеризующих условия
измерений, от установленного значения.
Субъективная (личная) погрешность измерения обусловлена погрешностью отсчета
оператором показаний по шкалам СИ, диаграммам регистрирующих приборов.
8

9.

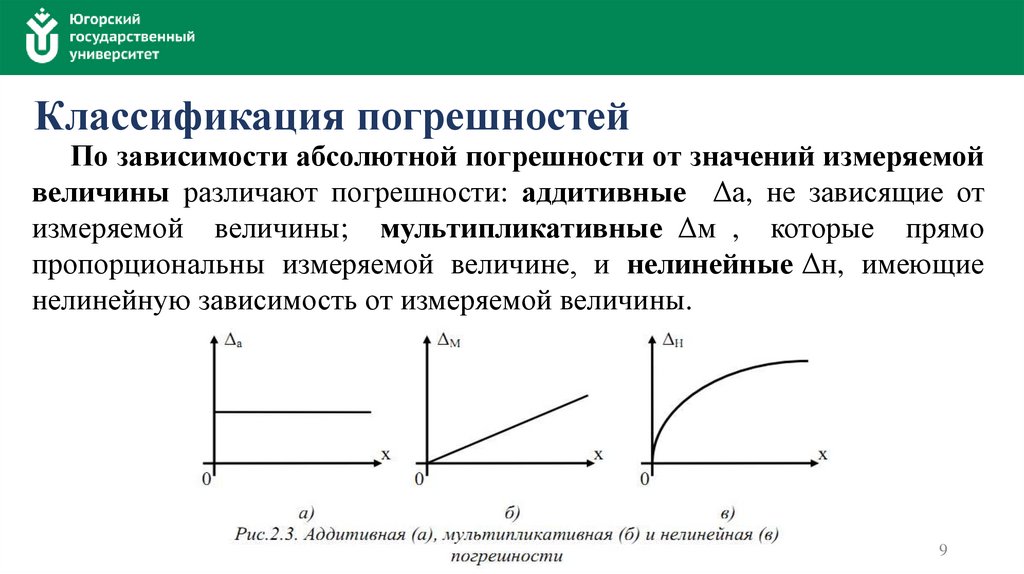
Классификация погрешностей
По зависимости абсолютной погрешности от значений измеряемой
величины различают погрешности: аддитивные Δa, не зависящие от
измеряемой величины; мультипликативные Δм , которые прямо
пропорциональны измеряемой величине, и нелинейные Δн, имеющие
нелинейную зависимость от измеряемой величины.
9

10.

Классификация погрешностей
По влиянию внешних условий
дополнительную погрешности СИ.
различают
основную
и
Основная погрешность средства измерений – погрешность СИ,
применяемого в нормальных условиях.
Дополнительная
погрешность
средства
измерений
–
составляющая погрешности СИ, возникающая дополнительно к
основной погрешности,
вследствие отклонения какой-либо из
влияющих величин от нормального ее значения или вследствие ее
выхода за пределы нормальной области значений.
10

11.

Классификация погрешностей
В зависимости от влияния характера изменения измеряемых
величин погрешности СИ делят на статические и динамические.
Статической называется погрешность средства измерений,
применяемого для измерения ФВ, принимаемой за неизменную.
Динамической называется погрешность СИ,
возникающая
дополнительно при измерении изменяющейся (в процессе измерений)
ФВ.
11

12.

Погрешность и неопределенность
Основные положения руководства:
отказ от использования таких понятий, как истинное и
действительное значения измеряемой величины, погрешность,
относительная погрешность, точность измерения, случайная и
систематическая погрешности;
- введение нового термина «неопределенность» – параметра,
связанного с результатом измерения и характеризующего рассеяние
значений, которые можно приписать измеряемой величине;
- разделение составляющих неопределенности на два типа А и В.
Вновь вводимые группы неадекватны случайным и систематическим
погрешностям.
Разделение
основано
не
на
теоретических
12
предпосылках, а на практических соображениях.

13.

Погрешность и неопределенность
Неопределенность (измерения) — параметр, характеризующий
разброс значений, которые могли бы быть обоснованно приписаны
измеряемой величине.
Расширенная неопределенность
13

14.

Погрешность и неопределенность
Неопределенности типа А могут быть оценены статистическими
методами на основе многократных измерений и описываются
традиционными характеристиками центрированных случайных величин
– дисперсией или СКО.
Неопределенности типа В могут быть оценены любыми другими
методами, кроме статистических.
14

15.

Погрешность и неопределенность
Общая схема оценивания расширенной
включает четыре основных этапа.
неопределенности
Первый этап — выявление и описание зависимости измеряемой
величины от параметров, от которых она зависит.
Второй этап — выявление источников неопределённости.
15

16.

Погрешность и неопределенность
Третий этап предполагает расчёт значения относительной стандартной неопределённости, присущей
каждому выявленному потенциальному источнику.
Относительная стандартная неопределённость (ai, %)
Где ഥ
Х — среднеарифметический результат анализа; Xk — k-ый результат анализа; n — количество параллельных определений.
Где Δ — предел погрешности используемого средства измерения; x — величина измеряемого аналитического сигнала; p — коэффициент,
зависящий от принятой функции распределения.
Выбор функции распределения зависит :
1. Известны только пределы погрешности используемого средства измерения, а форма распределения неизвестна. р= 3.
2. Известны пределы погрешности используемого средства измерения и есть основание ожидать, что значения в центре диапазона более
вероятны, чем вблизи границ, т. е. функция распределения — треугольная. р= 6.
3. Известен интервал, охватывающий определённую долю распределения вероятности, например, 95 %. р=2.
16

17.

Погрешность и неопределенность
Четвёртый этап — вычисление расширенной неопределённости (U).
Суммарная стандартная неопределенность (∑u):
где С — результат химического анализа
Значение U получают
коэффициент охвата k:
умножением
суммарной
стандартной
неопределенности (u ) на
Результат химического анализа может быть записан в следующем виде:
где С — результат химического анализа; U — расширенная неопределенность (k = 2).
17

18.

Погрешность и неопределенность
Задача
Рассмотрим вышеописанную схему оценивания расширенной
неопределенности
на
примере методики
титриметрического
определения концентрации соляной кислоты.
Методика предполагает титрование аликвот анализируемого
раствора соляной кислоты раствором гидроксида натрия. При этом
проводят предварительное определение концентрации
раствора
гидроксида натрия титрованием навесок щавелевой кислоты.
18

19.

Результат измерений и его характеристики
Результат измерения физической величины — это значение физической величины, найденное путем ее измерения.
Выделяют 5 основных характеристик результатов измерений:
1. Точность — степень близости результата измерений к истинному (или в его отсутствии принятому опорному) значению измеряемой величины.
2. Правильность — степень близости среднего значения, полученного из большой серии результатов измерений, каждое из которых может состоять из
нескольких наблюдений, к истинному значению измеряемой величины.
3. Прецизионность — степень близости друг к другу независимых результатов измерений одной и той же величины, полученных при конкретных
регламентированных условиях их выполнения.
4. Повторяемость (сходимость) — прецизионность результатов измерений в условиях повторяемости, когда результаты измерения получают по одной
и той же методике на идентичных объектах (образцах), в одной и той же лаборатории, одним и тем же оператором, с использованием одного и того же
оборудования и средств измерений в пределах короткого интервала времени (нескольких часов).
5. Воспроизводимость — прецизионность результатов измерений в условиях воспроизводимости, когда результаты измерения получают по одной и тем же
методике на идентичных объектах, но в разных лабораториях, различными операторами, с использованием различного оборудования, средств измерений и
реактивов.
Вутрилабораторная прецизионность — прецизионность в условиях, когда результаты измерения получают по одной и той же методике на
19
идентичных объектах измерения и в одной лаборатории, но разными операторами, в разное время и с использованием различного оборудования
и
реактивов.

20.

Представление результатов измерений
Как правильно представить результат?
9,8 ± 0,2 г/л
9,8 г/л
(9,8 ± 0,2) г/л
9,8 г/л ± 0,2 г/л
20

21.

Правила округления результатов измерений
1. Результат измерения округляется до того же десятичного знака,
которым оканчивается округленное значение абсолютной погрешности.
Если десятичная дробь в числовом значении результата измерений
оканчивается нулями, то нули отбрасываются до того разряда, который
соответствует разряду числового значения погрешности.
Пример: Число 999,99872142 при погрешности ±0,000005 следует
округлять до 999,998721.
21

22.

Правила округления результатов измерений
2. Если цифра старшего из отбрасываемых разрядов меньше 5, то
остальные цифры числа не изменяются. Лишние цифры в целых числах
заменяются нулями, а в десятичных дробях отбрасываются.
Пример: При сохранении четырех значащих цифр число 283435 должно
быть округлено до 283400; число 384,435 – до 384,4.
22

23.

Правила округления результатов измерений
3. Если цифра старшего отбрасываемого разряда больше или равна 5, но за
ней следуют отличные от нуля цифры, то последнюю оставляемую
цифру увеличивают на единицу.
Пример: При сохранении трех значащих цифр число 17,58 округляют до
17,6; число 18598 – до 18600; число 352,521 – 353.
23

24.

Правила округления результатов измерений
4. Если отбрасываемая цифра равна 5, а следующие за ней цифры
неизвестны или являются нулями, то последнюю сохраняемую цифру числа
не изменяют, если она четная, и увеличивают на единицу, если она нечетная.
Пример: При сохранении трех значащих цифр число 264,50 округляют до
264; число 645,5 – до 646.
24

25.

Правила округления результатов измерений
5. Округление производится лишь в окончательном ответе, а все
предварительные вычисления проводят с одним-двумя лишними знаками.
25

26.

Спасибо за внимание!