Похожие презентации:
Динамика. Законы Ньютона
1.
ДинамикаЗаконы Ньютона
лекция 1
© Парфентьева Наталия Андреевна
2.
Динамика – раздел механики, в которомизучается движение тел под действием
приложенных к ним сил.
Основной задачей динамики является
определение закона движения тела
по известным взаимодействиям с другими
телами.
Обратная задача – по известному закону
движения тела определить силы, действующие
на него.
3.
Могила Исаака Ньютона (1643-1727)Вестминстерское аббатство
«Тут покоится
сэр Исаак Ньютон,
дворянин, который
почти божественным
разумом первый
доказал с факелом
математики
движение планет,
пути комет,
и приливы океанов...
Пусть смертные
радуются, что
существовало такое
украшение рода
человеческого».
4.
Памятник Ньютонув церкви колледжа Троицы
в Кембридже.
Он был тем, кто исследовал
различия световых лучей
и проистекающие из них
различные свойства цветов,
о которых прежде никто
и не подозревал.
Прилежный, хитроумный
и верный истолкователь
природы, древности
и Святого Писания,
он утверждал своей
философией величие
всемогущего творца,
а нравом насаждал
требуемую Евангелием
простоту.
«Разумом он превосходил
род человеческий».
5.
Памятники НьютонуВеликобритания, 19-ое мая 2016:
Исаак Ньютон. Eduardo Paolozzi
в Британской библиотеке в
Лондоне.
Почтение Ньютону. Сальвадор Дали
Испания. Север Каталонии
6.
«Не знаю, как меня воспринимает мир,но сам себе я кажусь только мальчиком,
играющим на морском берегу, который
развлекается тем, что время от времени
отыскивает камешек более пёстрый, чем
другие, или красивую ракушку, в то время
как великий океан истины расстилается
передо мной неисследованным».
«Я не вижу ничего желательного в славе,
даже если бы я был способен заслужить её.
Это, возможно, увеличило бы число моих
знакомых, но это как раз то, чего я больше
всего стараюсь избегать».
Исаак Ньютон
7.
28 апреля 1686 года выход первого тома.«Математические начала натурфилософии»
8.
ОСНОВНЫЕ ПОНЯТИЯДИНАМИКИ
9.
1. Масса m является количественноймерой инертности тел.
Инертность – свойство разных тел по-разному
изменять свою скорость под действием одной
и той же силы. Единицей массы в СИ является
килограмм.
Масса является мерой гравитационного
взаимодействия тел.
mин = mгр
10.
Международныйэталон килограмма,
сделан в виде цилиндра,
имеющего диаметр
и высоту 39,17 мм.
Материал – сплав,
содержащий
90 % платины
и 10 % иридия.
Эталон хранится
в штаб-квартире
Международного бюро
мер и весов в Севре.
11.
2. Сила – количественная меравзаимодействия тел. Следовательно,
если на тело действует сила, то это
означает, что есть второе тело,
с которым оно взаимодействует.
Единицей силы в Международной
системе единиц (СИ) является Ньютон.
В СИ
кг м
1Н
2
с
12.
Основное утверждение механики:любое изменение движения тела есть
результат действия на него других тел.
Воздействие одного тела на другое может
происходить при непосредственном
соприкосновении тел или посредством
силовых полей – поля тяготения,
электрическое и магнитное поля.
13.
Силы в механике1) Сила тяготения.
Все тела притягиваются друг к другу.
Для материальных точек (или шаров)
закон всемирного тяготения:
F Gm1m2 / r122
14.
Если тело массы m находитсянад поверхностью Земли на высоте h,
то на него действует сила тяготения, равная
F = GmM3/(R3 + h)2, где M3 – масса Земли,
R3 – радиус Земли.
15.
После обеда установилась тёплая погода,мы вышли в сад и пили чай в тени яблонь.
Он (Ньютон) сказал мне, что мысль
о гравитации пришла ему в голову,
когда он точно так же сидел под деревом.
Он находился в созерцательном
настроении, когда неожиданно
с ветки упало яблоко. «Почему яблоки
всегда падают перпендикулярно земле?» –
подумал он.
16.
2) Сила тяжести Fт определяется силой притяжения телак Земле и тем, что Земля вращается вокруг собственной оси.
В связи с малым значением угловой скорости вращения Земли
(ω = 7,27 10–3 c–1) сила тяжести мало отличается от силы
тяготения. При h << R3 ускорение, создаваемое силой
тяжести, является ускорением свободного падения:
g = GM3/R23 = 9,82 м/с2 на полюсе и g = 9,78 м/с2
на экваторе.
17.
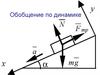
3) Весом тела называется сила, с которой тело,вследствие его притяжения Землей, действует
на опору или растягивает подвес.
Эта сила приложена либо к опоре, либо к подвесу.
18.
4) Сила, вызванная деформацией тели препятствующая изменению объема тела,
называется силой упругости. Деформация
называется упругой, если после снятия внешнего
воздействия тело возвращается в исходное
состояние.
Fупр x = – kx, Fупр = + k x ,
где k – коэффициент
упругости (жесткость),
зависящий от свойств
материала и геометрии
деформируемого тела.
19.
Для характеристики упругих свойстввещества вводится модуль Юнга.
Напряжение , = F/S.
Относительная деформация = x/l0.
Закон Гука: = (1/Е) .
Физический смысл модуля Юнга:
величина Е численно равна
напряжению, возникающему в
твердом теле при относительной
деформации, равной единице.
20.
5) Сила трения. Трение, возникающеепри относительном перемещении сухих
поверхностей твердого тела, называется
сухим трением.
Три вида сухого трения: трение покоя,
скольжения и качения.
Fтр.покоя F
21.
Сила трения скольжения определяется из соотношения:Fтр = N,
где – коэффициент трения, зависящий от шероховатости
и от физических свойств соприкасающихся поверхностей,
N – сила нормальной реакции опоры, эта сила определяет
насколько тело прижато к поверхности, по которой
оно движется.
Сила трения покоя изменяется по величине
от 0 до максимального значения Fтр.покоя max .
22.
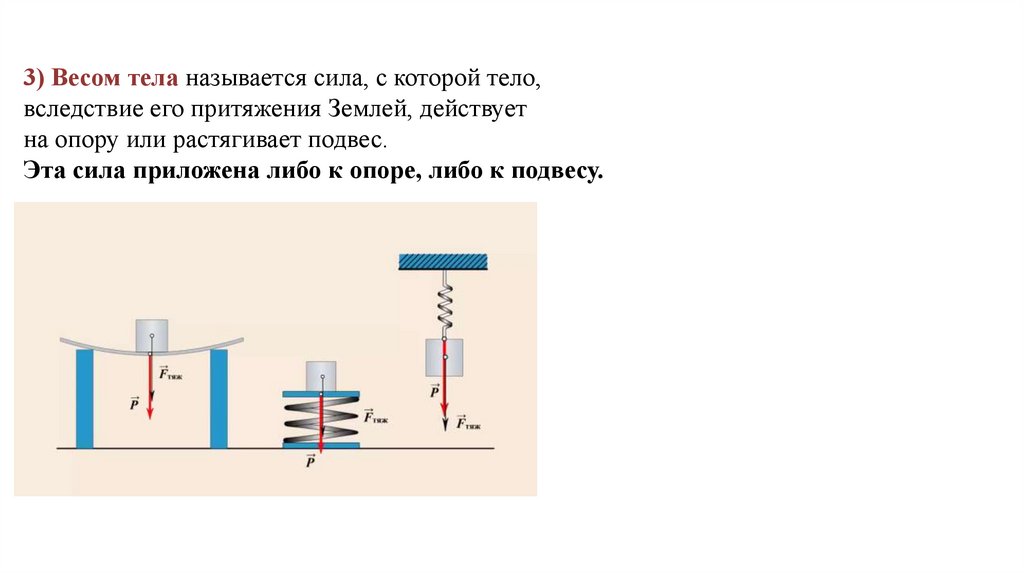
Зависимость силы трения от угла наклона доскиFтр.п. mg sin
Fтр.ск. mg cos
23.
Сила трения качения мала по сравнениюс силой трения скольжения. При больших
скоростях сопротивление перекатыванию резко
увеличивается и тогда следует считать силу
трения равной силе трения скольжения.
Сила трения качения определяется деформацией
колеса и опорной поверхности, а также адгезией
(межмолекулярным взаимодействием).
Силы трения и упругости вызваны силами
взаимодействия молекул.
24.
Законы НьютонаПервый закон Ньютона – закон инерции.
Стремление сохранять первоначальное
состояние –явление инерции.
25.
Второй закон НьютонаУскорение, с которым движется тело, прямо
пропорционально силе, действующей на тело,
и обратно пропорционально его массе
и совпадает по направлению с действующей силой:
a F / m.
Fрез F1 F2 F3 ...
maцт F1 F2 F3 ...
26.
Принцип суперпозиции сил27.
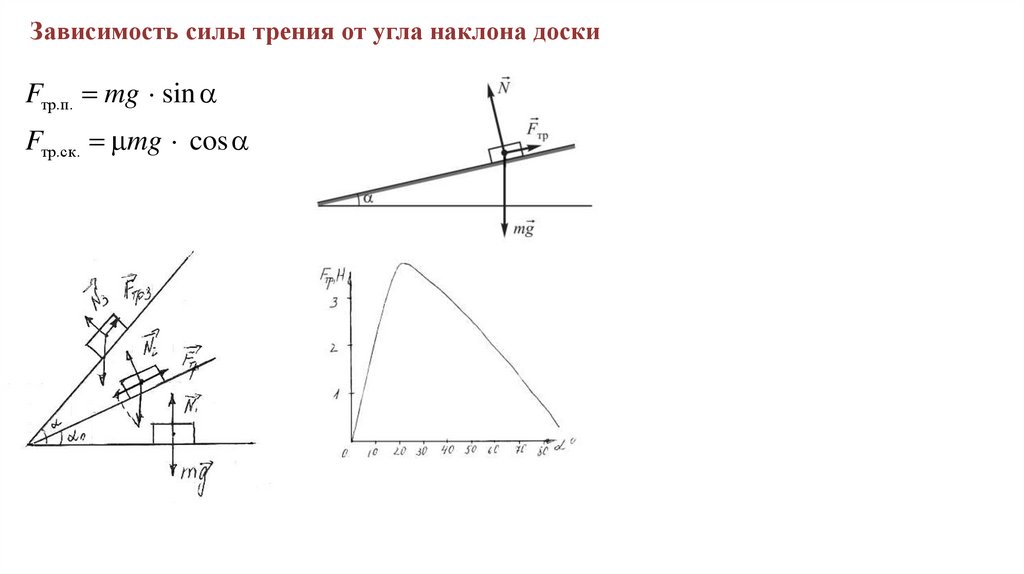
Третий закон НьютонаВсякому действию всегда есть равное
и противоположно направленное противодействие.
При взаимодействии двух тел А и В силы
взаимодействия 1) равны по модулю,
2) противоположны по направлению,
3) направлены вдоль одной прямой,
4) приложены к разным телам
5) имеют одинаковую физическую природу
и 6) время их действия одинаково.
28.
Первый закон Ньютона необходим для того,чтобы определить те системы отсчета, в которых
справедливо основное утверждение механики.
Сила инерции. Эта сила не является
результатом взаимодействия тел, а является
результатом того, что мы рассматриваем
движение тела относительно системы отсчета,
движущейся с ускорением.
29.
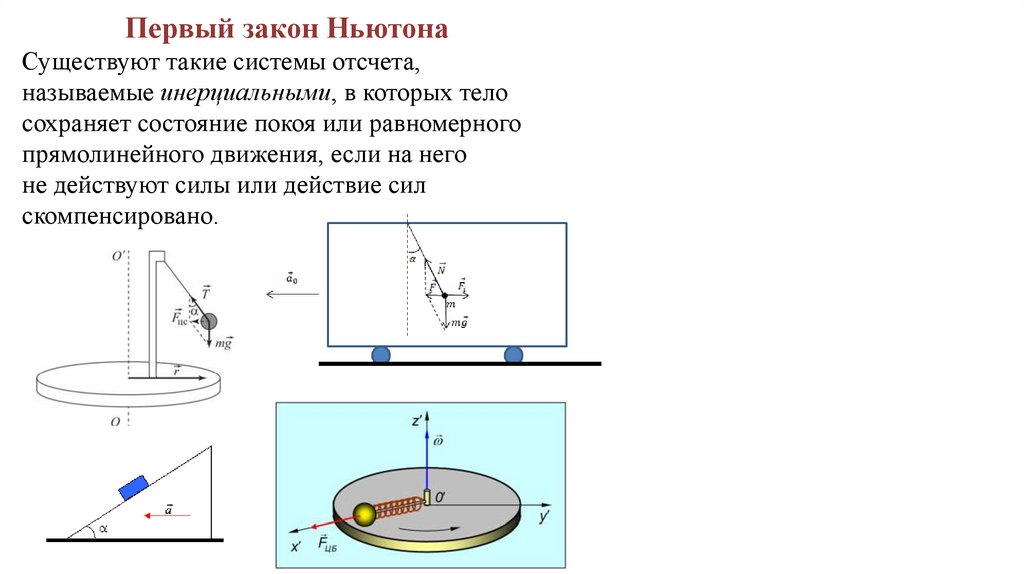
Первый закон НьютонаСуществуют такие системы отсчета,
называемые инерциальными, в которых тело
сохраняет состояние покоя или равномерного
прямолинейного движения, если на него
не действуют силы или действие сил
скомпенсировано.
30.
ДинамикаЗаконы Ньютона
лекция 2
31.
Примеры решения задачЗадачи о движении тела делятся на два типа:
1) известны взаимодействия данного тела
с другими телами, требуется определить
ускорение тела, а также другие кинематические
характеристики движения;
2) обратная задача – известно ускорение и часть
сил, действующих на тело, требуется
определить неизвестные силы.
32.
План решения задач:1) определить тела, с которыми данное тело взаимодействует;
2) сделать рисунок, на котором необходимо изобразить все
силы, действующие на тело. При этом все силы должны быть
приложены к центру масс тела, т.к. мы рассматриваем здесь
только его поступательное движение;
3) выбрать систему отсчета, а затем систему координат;
4) записать уравнение согласно закону Ньютона сначала
в векторной форме, а затем в проекциях на оси координат;
5) составить систему уравнений, при этом число
уравнений должно быть равно числу неизвестных;
6) определить неизвестные физические величины;
7) проверить их наименование;
8) сделать расчет, при этом нужно всегда иметь в виду,
что числовой ответ должен быть физически грамотным.
33.
Задача 1. Санки массой 10 кг тянутза веревку силой 50 Н, направленной
под углом 30 к горизонту. Определите
ускорение санок. Коэффициент трения
скольжения 0,03.
Решение.
ma mg N Fтр T
на ось ОХ : ma x Tcos Fтр Fтр N
на ось ОУ : 0 N Tsin μg
N mg Tsin , Fтр μ ( mg Tsin )
ma x Tcos μ ( mg – Tsin )
ax
T cos μ mg T sin
m
4,1 м / с .
2
34.
Задача 2. Лыжник начинает спускатьсяпо склону, который образует угол 30 с
горизонтом. Определите ускорение лыжника.
Коэффициент трения скольжения 0,1.
Решение.
На лыжника действуют силы:
Fт mg , N , Fтр
ma mg N Fтр Fтр N
на ось ОХ : max mgsinα Fтр
на ось ОУ : 0 N – mg cos α
max mg (sinα μ cos α)
ax g (sinα μ cos α) 4,0 м / с 2
35.
Задача 3. Определите отношение временподъема и спуска шайбы, запущенной вверх
по ледяной горке с углом наклона 20 .
Начальная скорость шайбы 8 м/с.
Коэффициент трения равен 0,1.
Решение.
ma N mg Fтр.
При подъеме
max1 mg sinα μmg cosα
ax1 g (sinα μ cosα)
При спуске
max 2 mg sinα – μ mg cosα
ax 2 g (sinα – μ cosα)
36.
Уравнение движения шайбы(движение вверх):
37.
при спуске2
a2t2сп
S
2
g sin μ cos
v02
2 g sin cos
2
v02
t2 сп
g 2 sin 2 2 cos 2
t1под
t2 сп
2
2
2
sin
cos
sin cos
sin cos
0,75
sin cos
38.
Задачи о движении системы телПлан решения задач динамики при
рассмотрении системы тел такой же,
как и для одного тела.
Необходимо рассматривать силы,
действующие на каждое тело
в отдельности, и также для каждого
тела записывать уравнения динамики.
39.
Примеры решения задачЗадача 4. Два бруска нижний массой 0,4 кг,
а верхний массой 0,2 кг поместили на наклонную
плоскость с углом наклона 45 , как показано
на рисунке. Коэффициент трения нижнего бруска 1,
верхнего – 0,1. Определите силу давления верхнего
бруска на нижний.
Решение.
m1a m1 g N1 Fтр1 F12
m2 a m2 g N 2 Fтр2 F21
a1 g (sin 1 cos )
a2 g (sin 2 cos )
40.
на ось ОХ : m1a m1 g sin Fтр1 F12m2 a m2 g sin Fтр2 F21
на ось ОУ : 0 m1 g cos N1
0 m2 g cos N 2
m1a m1 g sin 1m1 cos F12
m2 a m2 g sin 2 m2 cos F12
1 2 m1m2 g cos
F12
0,83 Н
m1 m2
41.
Задача 5. На доске массой m1 = 1 кг лежитбрусок массой m2 = 200 г. Определите,
с какой максимальной горизонтальной
силой можно тянуть доску, чтобы брусок
не соскользнул с нее. Коэффициенты трения
скольжения между доской и полом
μ1 = 0,2; между доской и бруском μ2 = 0,3.
Решение.
v1 = v2 = at, скорость бруска относительно
доски равна нулю.
Fтр2 Fтр2
42.
m1a1 F m1 g Fд N1 Fтр1 F2m2 a2 m2 g N 2 Fтр2
m1a1 F Fтр1 Fтр2
m2 a2 Fтр2
0 N 2 – m2 g
0 N1 – Fд – m1 g
Fд N 2
Fтр2 μ 2 m2 g
Fтр1 μ1 m1 m2 g
43.
m2a2 = 2m2gm1a1 = F – 1(m1 + m2)g – 2 gm2
a1 = a 2 = a
m1a = F – 1(m1 + m2)g – 2gm2
m2a = 2m2g
F = (m1 + m2)( 1 + 2)g
(Fтр. п. Fтр. ск. )
44.
Задача 6. Система тел m1 и m2 движется вместесо столом с ускорением a = 2 м/с2, направленным
вертикально вверх. Массы тел равны m1 = 1 кг,
m2 = 2 кг, коэффициент трения = 0,2. Чему
равно натяжение нити Т? С каким ускорением
должен двигаться стол, чтобы система этих тел
была относительно него неподвижна?
Решение.
m1a1 T1 N m1 g Fтр
m2 a2 T2 m2 g
Т1 Т 2 Т
m1a1x Т – Fтр
m1a N – m1 g
m2 a2 Т – m2 g
Fтр μ1 N m1 ( g a )
1
2
3
45.
m1a1 Т – m1 g am2 a1 a m2 g T
(m1 m2 )a1 m2 a m1 g a m2 g
a g m2 m1
a
1
m1 m2
В неинерциальной системе отсчета,
связанной со столом
m1a1отн T1 N m1 g Fтр Fин1
m2 a2отн T2 m2 g Fин2
Fин1 m1a Fин2 m2 a
46.
аотн = а1а2 = – аотн + а
N = m1 (a + g); Fтр = m1(а + g)
m1аотн = Т – (а + g)m1
m2(– аотн + а) = Т – m2g
– m2аотн = Т – m2(g + а)
aотн
(4)
(5)
m2 μm1 g a
m1m2 1 μ g a
;T
9,6 Н
m1 m2
m1 m2
47.
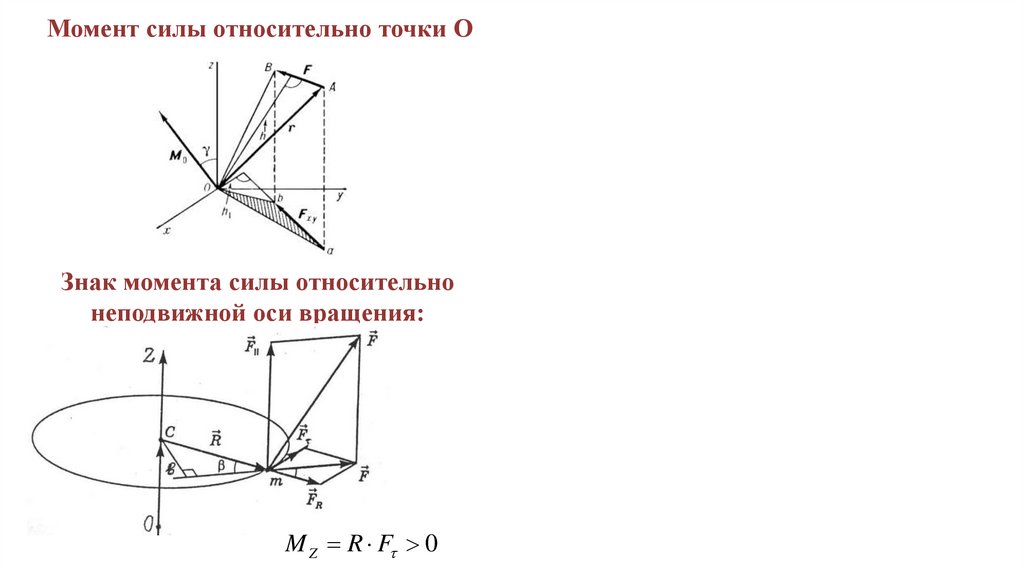
Динамика вращательного движенияОсновные понятия
Момент силы относительно неподвижной оси вращения:
M r F
M F r sin α F d Fк r
Сила и радиус вектор принадлежат
одной плоскости
Момент силы перпендикулярен
плоскости r и F
48.
Момент силы относительно точки ОЗнак момента силы относительно
неподвижной оси вращения:
M Z R F 0
49.
Движение тела относительнонеподвижной оси вращения
Сила направлена под углом к радиусу R
1. Проекция силы на плоскость XY – Fвнеш
на ось OZ – FII вызывает движение вдоль оси OZ.
2. Проекции силы F на оси ОX и ось OY– F0 и FꞱ ,
первая сила не вызывает вращения, т.к. прямая,
которой принадлежит
эта сила проходит через
ось вращения, а вторая
определяет ускорение
вращательного движения.
Момент этой силы равен
M = R FꞱ и направлен
вверх вдоль оси OZ.
50.
Вывод основного законадинамики вращательного движения
Выделим в теле малый объем массой mi,
будем считать, что тело состоит из малых
частей. Для выделенной массы запишем
mi ai Fi внеш Fi внутр
mi ri ai ri Fi внеш ri Fi внутр
ri ai ri ε ri ri 2 ε
m r ε M
2
i i
i внеш
M i внутр
2
m
r
i i ε M i внеш
i
i
M i внутр 0
i
2
mi ri ε M
i
51.
Момент инерцииМомент инерции системы материальных
точек определяется суммой произведений
масс всех точек на квадраты их расстояний
до оси вращения.
При определении момента инерции
твердого тела суммирование заменяется
интегрированием.
I mi ri 2
i
dm dV
I r 2 dV
V
Момент инерции тела характеризует
его инертность по отношению
к вращательному движению.
52.
Расчет момента инерции твердых тел1. Однородный диск
dm 2 hrdr
R
2
r
mR
I 2 h r 3dr 2 h
4 0
2
0
R
4
2. Однородный стержень
dm sdx
l /2
3
2
x
l
ml
I s x 2 dx s s
3 l /2
12 12
l /2
l /2
3
53.
Теорема ШтейнераМомент инерции тела относительно произвольной
неподвижной оси равен сумме момента инерции
этого тела относительно параллельной ей оси,
проходящей через центр масс тела и произведения
массы тела m на квадрат расстояния d между
осями.
I AA I OO md 2
I
– искомый момент инерции относительно параллельной оси,
AA
I
– известный момент инерции относительно оси,
OO
проходящей через центр масс тела,
m – масса тела,
d – расстояние между указанными осями
ml 2 ml 2 ml 2
I AA
12
4
3
54.
Основной закон динамикивращательного движения
M
ε
I
Задача 7. Через блок перекинута нерастяжимая нить,
к которой привязаны два груза 4 и 2 кг. Определите
ускорение, с которым движутся тела, а также их скорости
в тот момент, когда разность высот, на которых находятся
тела, станет равна 80 см. 1. Массами нити и блока пренебречь.
Решение.
M a1 mg T1
ma M g T2
Ma1x mg – T1
ma2 x Mg – T2
55.
Нить нерастяжима → a1x = a2x = a; a1x a; a2 x a.Нить невесома → T1 T1 , T2 T2
Блок невесом → T1 T2
T1 T1 T2 T2 T
ma T – mg ,
Мa Мg T .
M m
( M m) а ( M – m) g a
g
M m
h at 2
h
,t
v at ah
2
2
a
M m
v
gh
M m
56.
Задача 8. Через блок перекинута нерастяжимая нить,к которой привязаны два груза M = 4 кг и 2 кг.
Определите ускорение, с которым движутся тела,
а также их скорости в тот момент, когда разность высот,
на которых находятся тела, станет равна R = 80 см.
Массами нити пренебречь. Масса блока а) равна 0;
б) равна 1 кг.
Решение.
M a1 M g T1
ma2 m g T2
I M1 M 2
Ma Mg T1
ma T2 mg
2
m
r
I T r T r бл a T T r
1
2
1
2
2
r
57.
(m M mбл )a ( M m) g( M m) g
a
m M mбл
1
a1 g
3
2
a2 g
7
58.
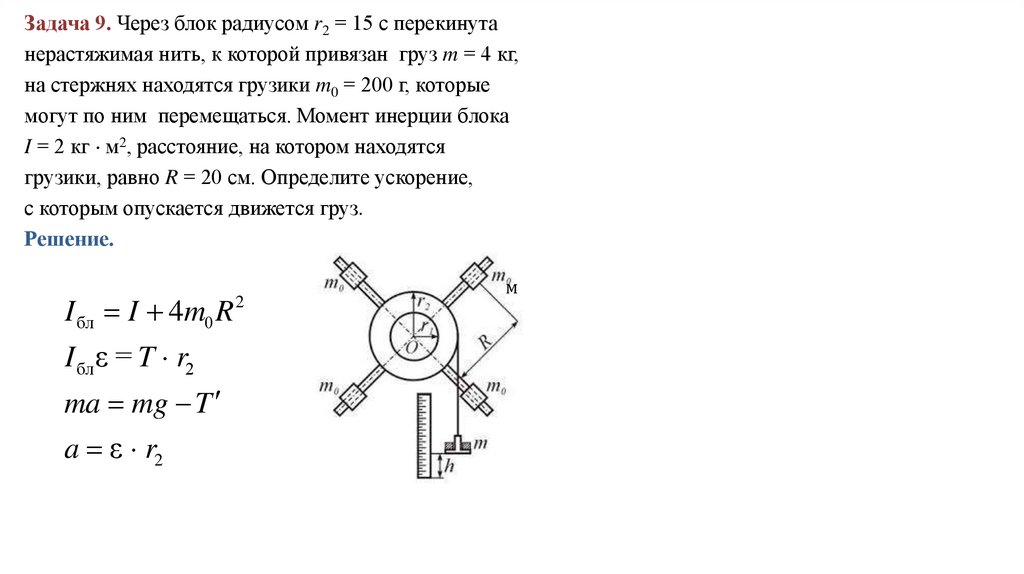
Задача 9. Через блок радиусом r2 = 15 с перекинутанерастяжимая нить, к которой привязан груз m = 4 кг,
на стержнях находятся грузики m0 = 200 г, которые
могут по ним перемещаться. Момент инерции блока
I = 2 кг м2, расстояние, на котором находятся
грузики, равно R = 20 см. Определите ускорение,
с которым опускается движется груз.
Решение.
I бл I 4m0 R
I блε = T r2
ma mg T
a ε r2
2
м



































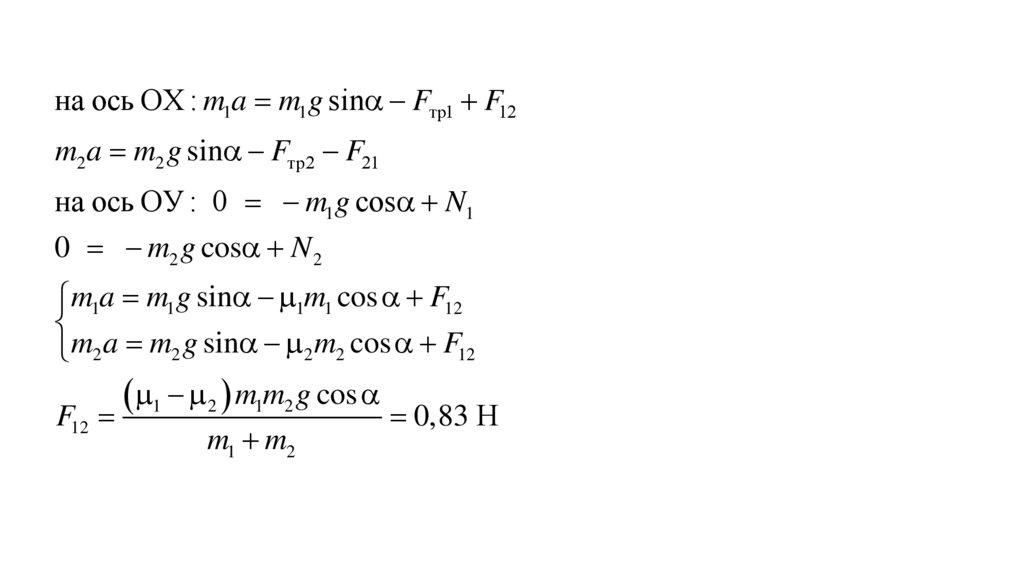
















 Физика
Физика