Дифракция света. Дифракция Фраунгофера

1.

Лекция № 12
Дифракция света
Дифракция Фраунгофера

2.

Фраунгофер Йозеф
1787- 1826
Немецкий физик.
Научные работы относятся к
физической оптике.
Внёс существенный вклад в
исследование дисперсии и создание
ахроматических линз.
Фраунгофер изучал дифракцию в
параллельных лучах (дифракция
Фраунгофера)
с начала от одной щели, а потом от
многих.
Большой заслугой учёного является
использование с 1821 года
дифракционных решеток для
исследования спектров.

3.

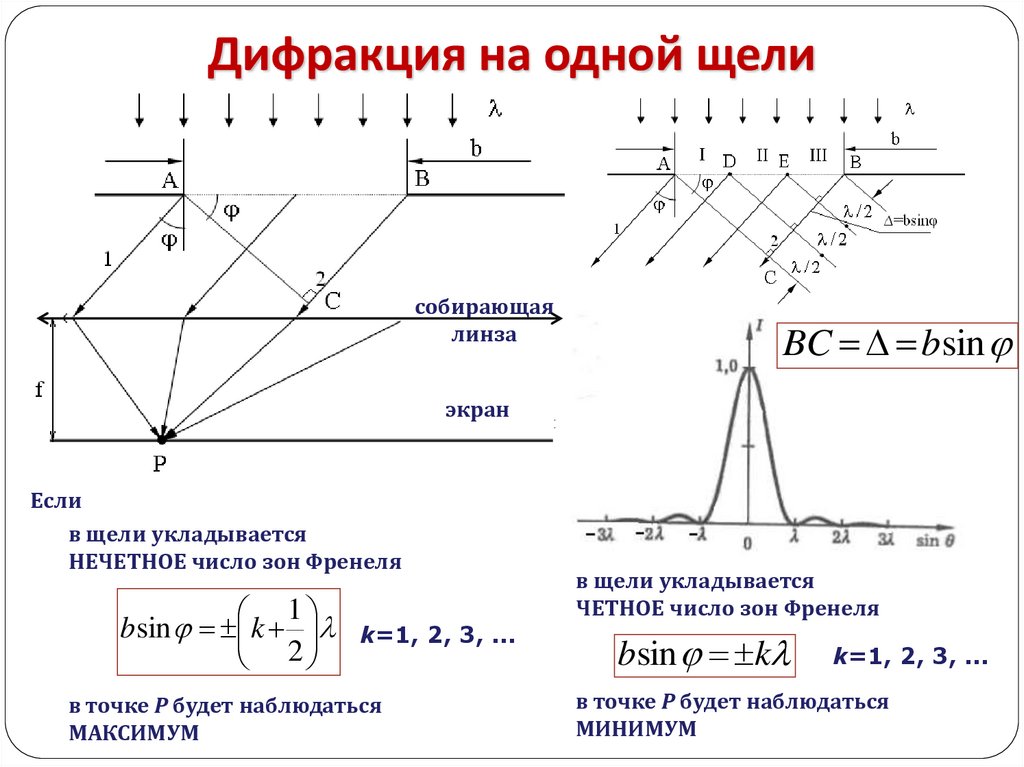
Дифракция на одной щели
собирающая
линза
BC b sin
экран
Если
в щели укладывается
НЕЧЕТНОЕ число зон Френеля
1
b sin k
2
k=1, 2, 3, …
в точке Р будет наблюдаться
МАКСИМУМ
в щели укладывается
ЧЕТНОЕ число зон Френеля
b sin k
k=1, 2, 3, …
в точке Р будет наблюдаться
МИНИМУМ

4.

Дифракция Фраунгофера (1820) –
дифракция в параллельных лучах
Дифракция Фраунгофера на одной щели
b
sin 2 sin
.
J J 0
2
b
sin
Условие дифракцион ных минимумов :
b
sin k , b sin k , k 1,2,3...
между ними расположен ы максимумы :
b sin 2k 1 , их интенсивно сти
2
Joseph Fraunhofer
(1787-1826)
2
2
2
J 0 J 1 J 2 J 3 ... 1 32 52 72 ...
3 2
b b b
0
b
2
b
3
sin
b

5.

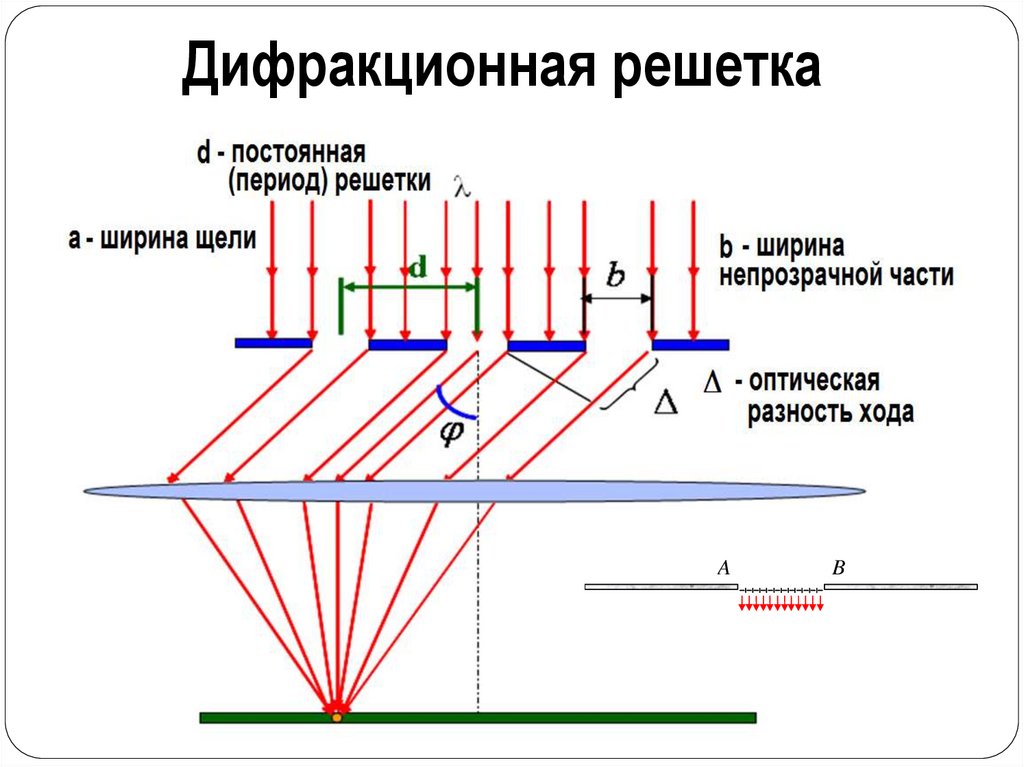
Дифракционная решетка
A
A
B
B

6.

Дифракционная решетка спектральный прибор, который раскладывает белый
свет в спектр
d sinφ =±m - главные максимумы
m= 0, 1, 2, 3 …
d sinφ =±(2m+1) /2 – дополнительные
минимумы
m=0, 1, 2, 3 …

7.

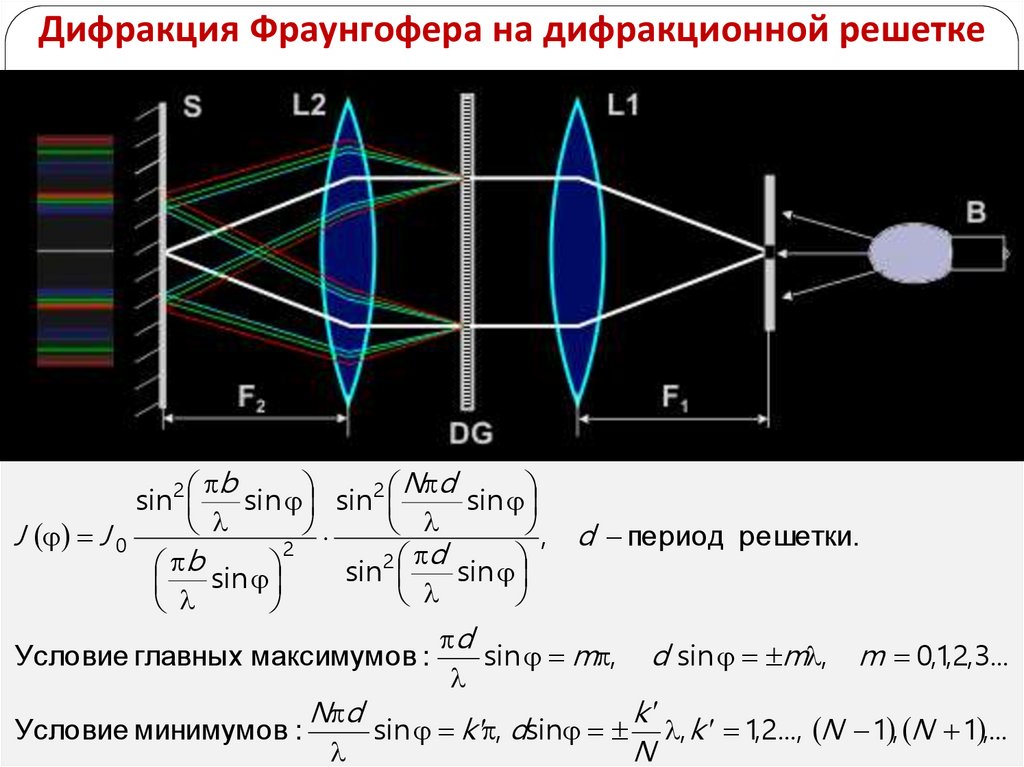
Дифракция Фраунгофера на дифракционной решетке
b
N d
sin2
sin sin2
sin
, d период решетки.
J J 0
2
2 d
b sin
sin
sin
d
Условие главных максимумов :
sin m , d sin m , m 0,1,2,3...
N d
k
Условие минимумов :
sin k , dsin , k 1,2..., N 1 , N 1 ,...
N

8.

Дифракционная решетка
Дифракционная решетка
Совокупность большого числа одинаковых щелей,
расположенных друг от друга
на одинаковом расстоянии
d – постоянная (или период) дифракционной
решетки
Уравнение главных МАКСИМУМОВ
d sin 2k
2
k k=1, 2, 3, …
с ↑ числа щелей в
дифракционной решетке:
• амплитуды добавочных max
↓
• угловая ширина
центрального max ↓

9.

Дифракционный спектр
Спектры, начиная со второго порядка, перекрываются
спектр
третьего
порядка
k=-3
спектр
второго
порядка
k=-2
спектр
первого
порядка
k=-1
max
нулевого
порядка
k=0
спектр
первого
порядка
k=1
спектр
второго
порядка
k=2
спектр
третьего
порядка
k=3

10.

Дифракционная решетка
как спектральный прибор
Основные характеристики спектрального прибора
Дисперсия
определяет угловое или линейное
расстояние между двумя
спектральными линиями
Угловая дисперсия численно равна углу между
двумя max одного порядка, отличающихся по λ
на 1 метр
d
D
у d
…
k
D
у d
угловое расстояние между
спектральными линиями,
отличающимися по длине волны на dλ
порядо
к max
период
решетк
и
Линейная дисперсия численно равна расстоянию на
экране между двумя max одного порядка,
отличающихся по λ на 1 м
dl
D
л d
линейное расстояние между
соседними max одного порядка,
отличающимися по длине волны на dλ
Dл fDу
фокусное
расстояние
линзы

11.

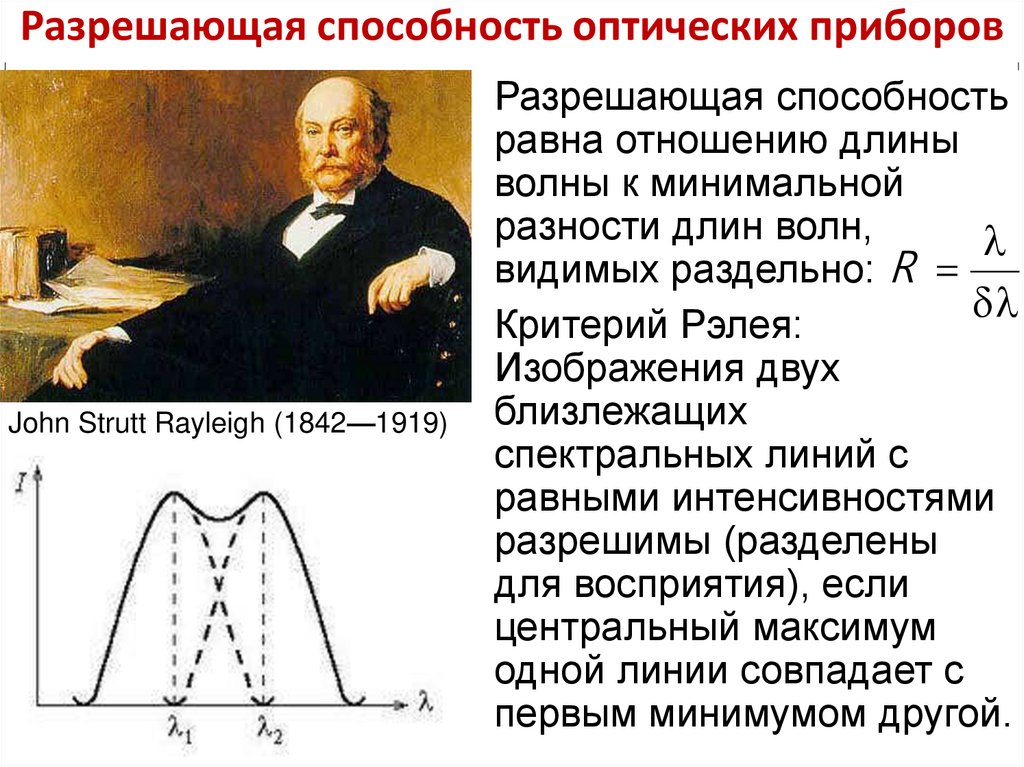
Разрешающая способность оптических приборов
John Strutt Rayleigh (1842—1919)
Разрешающая способность
равна отношению длины
волны к минимальной
разности длин волн,
видимых раздельно: R
Критерий Рэлея:
Изображения двух
близлежащих
спектральных линий с
равными интенсивностями
разрешимы (разделены
для восприятия), если
центральный максимум
одной линии совпадает с
первым минимумом другой.

12.

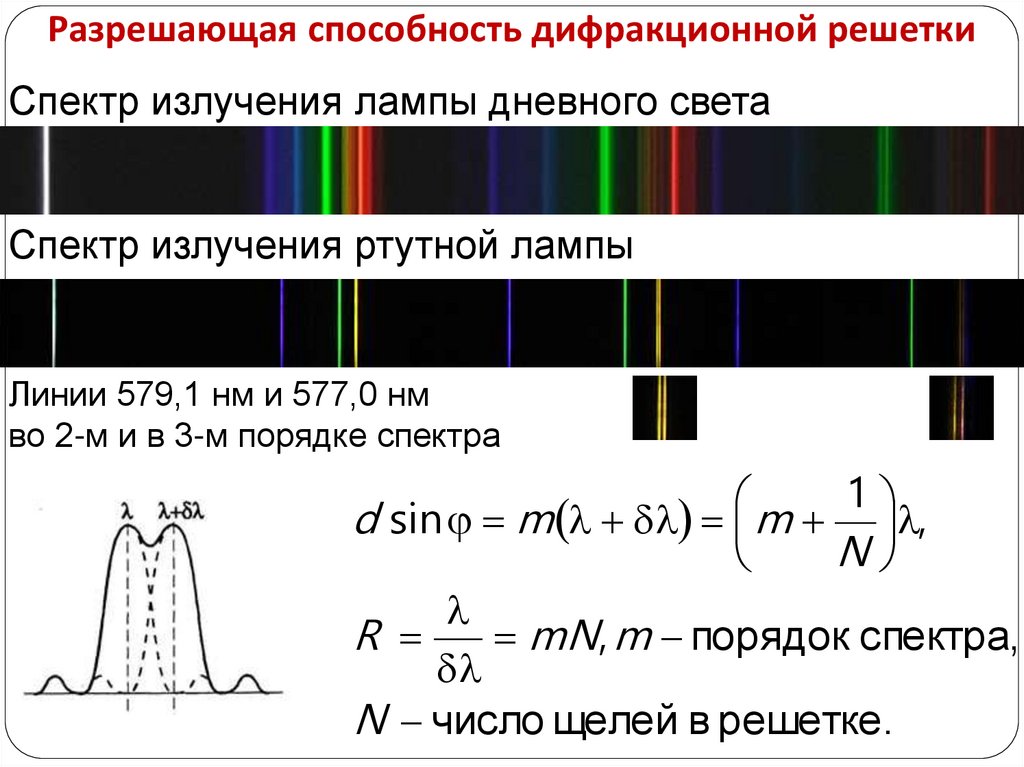
Разрешающая способность дифракционной решетки
Спектр излучения лампы дневного света
Спектр излучения ртутной лампы
Линии 579,1 нм и 577,0 нм
во 2-м и в 3-м порядке спектра
1
d sin m m ,
N
R
mN, m порядок спектра,
N число щелей в решетке.