Потенциал электрического поля

1. Потенциал электрического поля

Работа сил электрического
поля

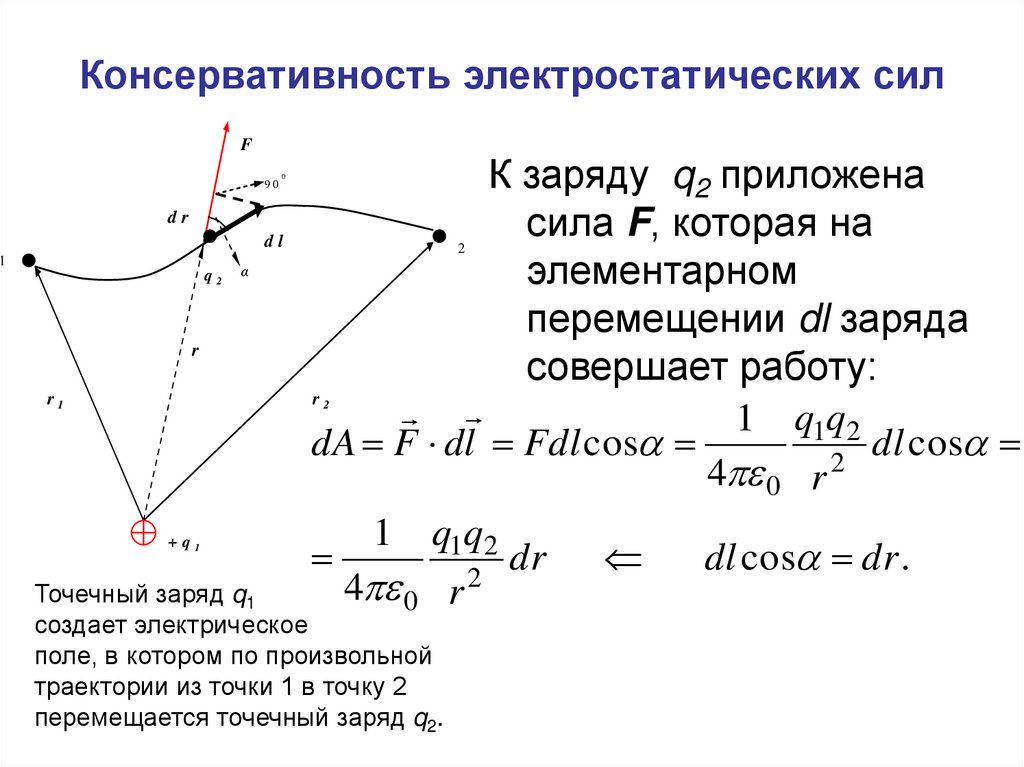
2. Консервативность электростатических сил

F
К заряду q2 приложена
dr
сила F, которая на
dl
q
элементарном
перемещении dl заряда
r
совершает работу:
r
r
1 q1q2
dA F dl Fdl cos
dl cos
2
4 0 r
1 q1q2
+q
dr
dl cos dr .
2
4 0 r
Точечный заряд q1
90
1
0
2
2
1
α
2
1
создает электрическое
поле, в котором по произвольной
траектории из точки 1 в точку 2
перемещается точечный заряд q2.

3. Консервативность электростатических сил

Работа, совершаемая при
перемещении заряда q2 из
точки 1 в точку 2:
F
90
0
dr
dl
1
q2
2
α
r2
r
r1
r2
q1q2 r dr
q1q2 1
A12 dA
2
4 0 r r
4 0 r
r
1
+q1
2
r2
r1
1
1 q1q2 q1q2
.
4 0 r1
r2
Работа А не зависит от траектории перемещения,
а определяется только положением начальной
и конечной точек.

4.

Электростатическое поле точечного заряда
является потенциальным, а
электростатические силы –
консервативными.
Работа, совершаемая при перемещении
электрического заряда в электростатическом
поле по любому замкнутому контуру
dA 0.
L

5. Потенциальная энергия взаимодействия двух зарядов

• Тело, находящееся в потенциальном поле,
обладает потенциальной энергией.
• Работу сил электростатического поля можно
представить, как разность потенциальных
энергий
q1q2
1 q1q2
A12
U1 U 2
4 0 r1
4 0 r2
1

6. Потенциальная энергия взаимодействия двух зарядов

При удалении заряда в бесконечность
r2 = ∞
q1q2
0,
U=U2 =
4 0
1
потенциальная энергия заряда q2,
находящегося в поле заряда q1
U
на расстоянии r
q1q2
U
4 0
r
1
q 1 ·q 2 > 0
0
r
q 1 ·q 2 < 0

7. Потенциальная энергия заряда в поле системы зарядов

• Система точечных зарядов: q1, q2, …qn.
Расстояние от каждого заряда до некоторой
точки пространства: r1, r2, …rn.
Работа, совершаемая над зарядом q электрическим
полем остальных зарядов при его перемещении из
одной точки в другую, равна алгебраической сумме
работ, обусловленных каждым из зарядов в
отдельности:
qi q
1 qi q
А12 Аi .(1) Ai
.(2)
i 1
4 0 ri1 4 0 ri 2
n
1
ri1 – расстояние от заряда qi до начального положения заряда q,
ri2 – расстояние от заряда qi до конечного положения заряда q.

8. Потенциальная энергия заряда в поле системы зарядов

n qq
n qq
1
1
i
i
(1)→(2):
A12
4 0 i 1 ri1 4 0 i 1 ri 2
ri2 → ∞ U 2 0
dA dE p , dA A12
dE p U 2 U1
1 n qi q n
A12
U i U
4 0 i 1 ri i 1
Принцип суперпозиции для энергии.

9. Потенциал электростатического поля

• Потенциальная энергия заряда q в поле n
n
зарядов qi
qi
U q
i 1 4 0 ri
• Отношение U/q не зависит от величины
заряда q и является энергетической
характеристикой электростатического
поля, называемой потенциалом.

10. Потенциал электростатического поля

U
q0
Потенциал электростатического поля
Потенциал в точке электростатического поля –
физическая величина численно равная
потенциальной энергии единичного
положительного заряда, помещенного в эту
точку. Это скалярная величина.
В СИ φ измеряется в вольтах [В = Дж/Кл]
1 В – потенциал такой точки поля, в которой
заряд в 1 Кл обладает энергией 1 Дж.
Е - [Н/Кл = Н·м/Кл·м = (Дж/Кл)·(1/м) = В/м].

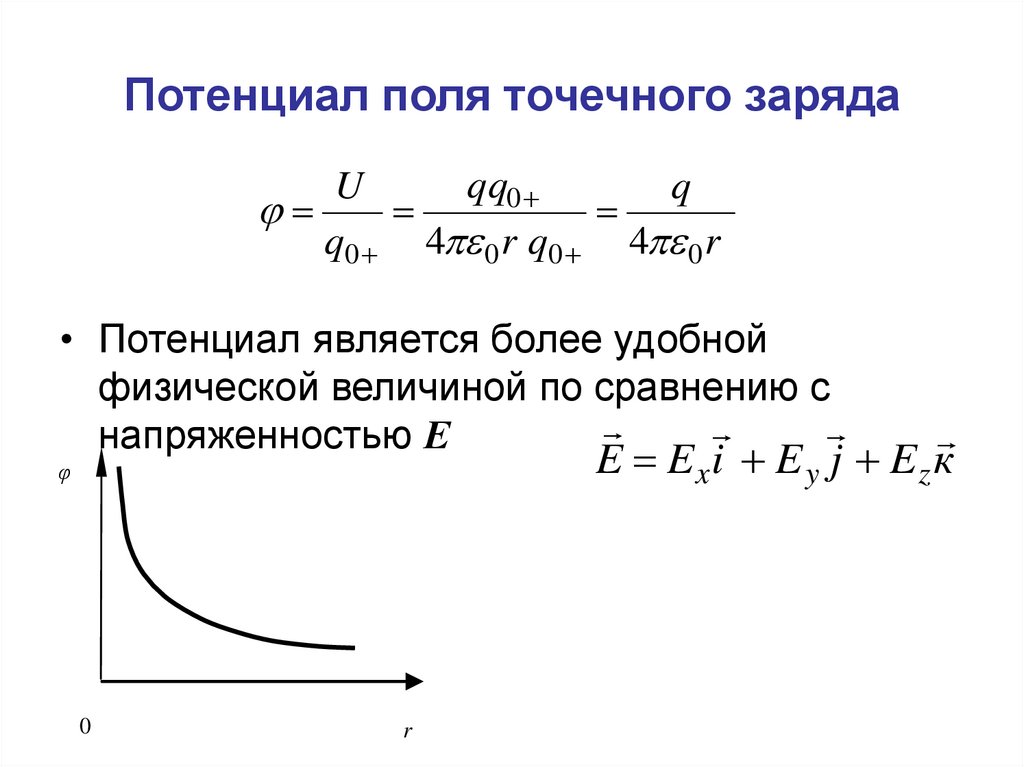
11. Потенциал поля точечного заряда

qq0
U
q
q0 4 0 r q0 4 0 r
• Потенциал является более удобной
физической величиной по сравнению с
напряженностью Е
E Ex i E y j Ez к
φ
0
r

12. Принцип суперпозиции для потенциалов

• Если электрическое поле создано системой
точечных зарядов, то потенциал φ в данной
точке равен алгебраической сумме
потенциалов φi, созданных в точке каждым из
зарядов в отдельности.
n
U
1 n qi
i
q
4 0 i 1 ri i 1

13. Разность потенциалов. Физический смысл потенциала

U
q0
φ2
φ1
При перемещении заряда q0+ в
электростатическом поле из
точки 1 в точку 2
A12 E p U1 U 2 q0 ( 1 2 )
r2
r1
r2 = ∞ → U2 = U∞ = 0
A1 U1 U q0 1 0 q0 1
0
A q0
A
q0

14. Физический смысл потенциала

A
q0
• Потенциал – физическая величина,
определяемая работой по перемещению
единичного положительного заряда из данной
точки в бесконечность.
Когда говорят о потенциале, то имеют ввиду
разность потенциалов ∆φ между
рассматриваемой точкой и точкой, потенциал
φ которой принят за 0.
Потенциал φ данной точки физического
смысла не имеет, так как нельзя определить
работу в данной точке.

15. Эквипотенциальные поверхности (поверхности равного потенциала)

1) во всех точках потенциал φ
имеет одно и то же значение,
2) вектор напряженности
электрического поля Е всегда
нормален к эквипотенциальным
поверхностям,
3) ∆φ между двумя любыми
эквипотенциальными
поверхностями одинакова
(следовательно, густота эквипотенциальных поверхностей
характеризует значение вектора Е в разных точках).

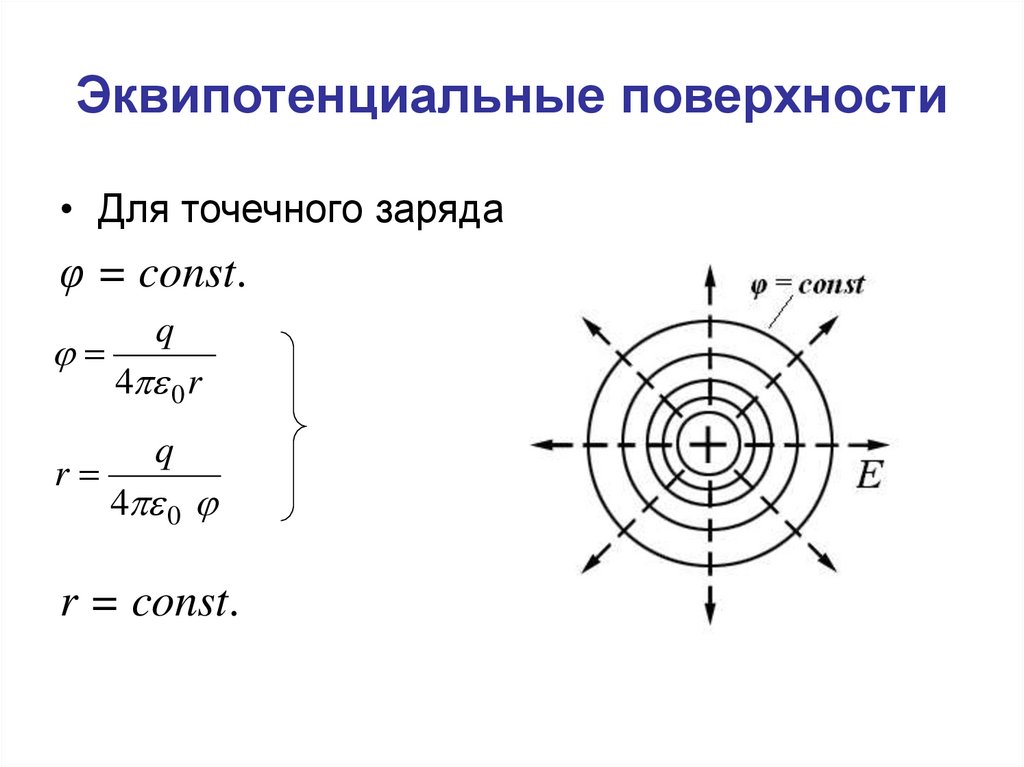
16. Эквипотенциальные поверхности

• Для точечного заряда
φ = const.
r
q
4 0 r
q
4 0
r = const.

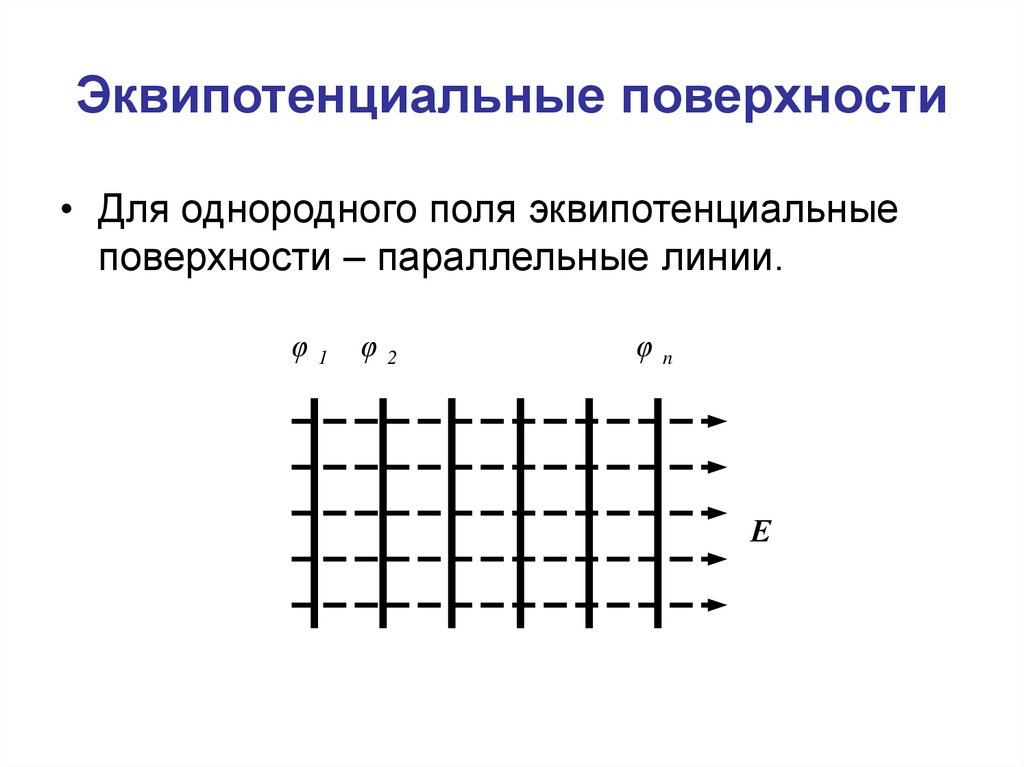
17. Эквипотенциальные поверхности

• Для однородного поля эквипотенциальные
поверхности – параллельные линии.
φ1
φ2
φn
Е

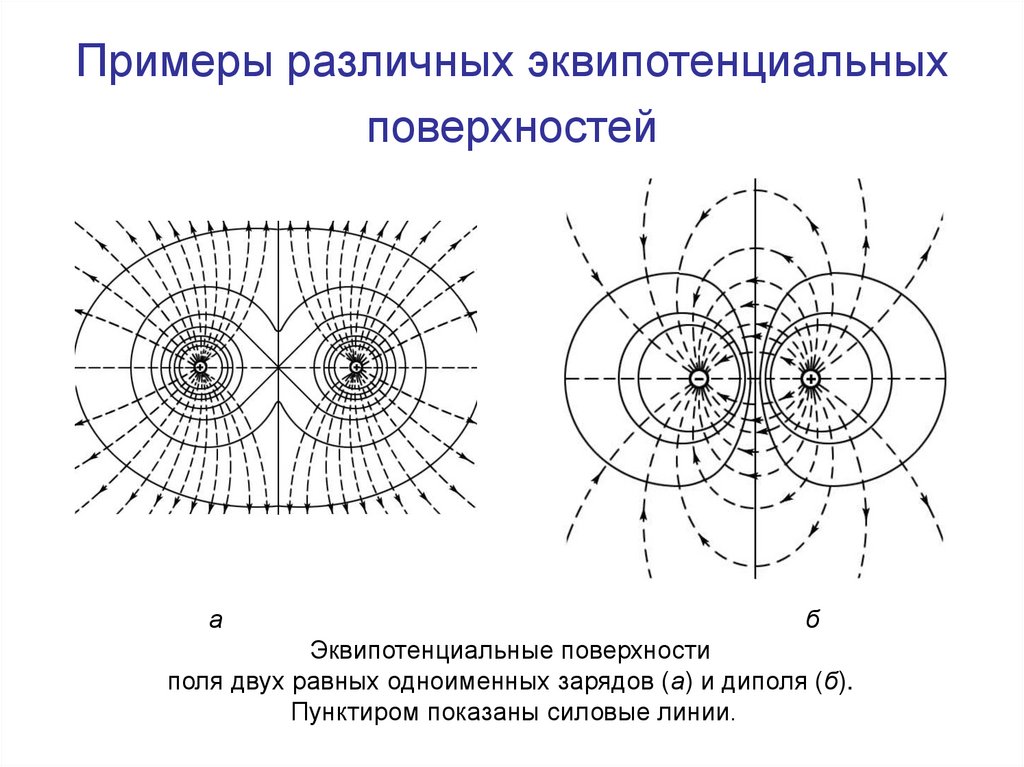
18. Примеры различных эквипотенциальных поверхностей

а
б
Эквипотенциальные поверхности
поля двух равных одноименных зарядов (а) и диполя (б).
Пунктиром показаны силовые линии.

19. Эквипотенциальные поверхности

• Работа по перемещению заряда
по эквипотенциальной
поверхности равна нулю.
A q( 1 2 ) q 0
так как
φ1 = φ2.

20. Эквипотенциальные поверхности

Е эквипотенциальной поверхности.
Работа при перемещении q по
эквипотенциальной
поверхности
A Fdl qE l cos( E , dl )
A q 0
qE l cos( E , dl ) 0
cos( E, dl ) 0
q 0,
E 0,
l 0
E, dl , E dl .
2
Вектор dl касательный к эквипотенциальной поверхности,
следовательно, вектор напряженности электрического
поля Е перпендикулярен эквипотенциальной поверхности.

21. Теорема о циркуляции вектора напряженности электрического поля Е

• Циркуляция вектора А: Adl Al dl
2 L
A12 Fdl q Edl
2
1
L
(1)
1
A12 q ( 1 2 )
• точки 1 и 2 совпадают
φ1 = φ2.
A12 q ( 1 2 ) 0
Из (1)
Ed l 0
L
Циркуляция вектора Е равна нулю.

22. Энергия взаимодействия системы зарядов

• Потенциальная энергия заряда q2
q1q2
U
4 0
r
1
• Энергия взаимодействия системы зарядов
1 n n 1 qi qk
W
;
2 i 1 k 14 0 rik
i k.
В формуле присутствует множитель ½, так как при
суммировании по всем i и k от 1 до n энергия
взаимодействия пар зарядов учитывается дважды.
i ≠ k, так как в случае i = k заряд
взаимодействует сам с собой.

23. Связь вектора напряженности Е и разности потенциалов. Третий способ определения напряженности электрического поля Е

• Работа по перемещению заряда в
электрическом поле:
dA Fdr qEdr ,
dA dE p dU .
(1)
Потенциальная энергия электрического поля
зависит от координат x, y, z и является
функцией U(x,y,z).

24. Связь вектора напряженности Е и φ

• При перемещении заряда на расстояние dr
его координаты изменяются :
(x+dx), (y+dy), (z+dz).
Изменение потенциальной энергии:
U
U
U
dU
dx
dy
dz
x
y
z
Из (1)
Fdr Fx dx Fy dy Fz dz
Fdr dU
(2)
(3)

25. Связь вектора напряженности Е и φ

U
Fx
x
U
Fy
y
U
Fz
z
(4)
F Fx i Fy j Fz к
(5)
U U U (6)
F
i
j
к
y
z
x

26. Связь вектора напряженности Е и φ

U U U
F
i
j
к
y
z
x
• Оператор набла (оператор Гамильтона):
F U E p
F
E ,
q
U
q
i
j к
x
y
z
E grad

27. Связь вектора напряженности Е и φ

E grad
grad
i
j
к
x
y
z
Знак «–» показывает, что
вектор Е направлен в
сторону убывания
потенциала.