Похожие презентации:
Электрическое поле в вакууме
1. 1.1 Электрический заряд и его свойства. Закон Кулона
ЛЕКЦИЯ 1. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ2. Электрический заряд
Электростатика – раздел учения об электричестве, изучающийвзаимодействие неподвижных электрических зарядов и свойства
постоянного электрического поля.
Электрический заряд – это внутреннее, индивидуальное свойство
тел или частиц, характеризующее их способность к
электромагнитному взаимодействию.
Электрический заряд q – физическая величина, которая определяет
интенсивность электромагнитного взаимодействия.
Единица электрического заряда – кулон (Кл) – электрический
заряд, проходящий через поперечное сечение проводника при силе
тока 1 А (ампер) за 1 с.
2
3. Свойства электрического заряда
1. Носители электрического заряда – заряженныеэлементарные частицы:
протон и электрон;
их античастицы – антипротон и позитрон;
нестабильные частицы - -мезоны, -мезоны и т.д.
Заряженные частицы взаимодействуют друг с другом с
силами, которые убывают с расстоянием так же медленно,
как гравитационные, но во много раз превышающими их по
величине.
3
4. Свойства электрического заряда
2. Электрический заряд аддитивен: заряд любой системы тел(частиц) равен сумме зарядов тел (частиц), входящих в
систему:
N
q q1 q 2 ... qi ... q N qi
i 1
Здесь i-номер заряда (тела или частицы); N – количество тел
(частиц) в системе.
4
5. Свойства электрического заряда
3. Электрический заряд дискретен: заряд q любого телакратен элементарному заряду e:
q Ne
Элементарный заряд: e = 1,602 10-19 Кл.
Поскольку тело не может приобрести или потерять долю
электрона, суммарный заряд тела должен быть целым
кратным элементарного заряда. Говорят, что заряд квантуется
(т.е. может принимать лишь дискретные значения).
Однако, поскольку заряд электрона очень мал, мы обычно не
замечаем дискретности макроскопических зарядов (заряду 1
мкКл соответствуют примерно 1013 электронов) и считаем
заряд непрерывным.
5
6. Свойства электрического заряда
4. Электрический заряд существует в двух видах –положительный и отрицательный. Одноименные заряды
отталкиваются, разноименные заряды притягиваются.
За положительный заряд принят заряд протона (+e). Заряд
электрона – отрицательный ( –e).
Если в состав макроскопического тела входит различное
количество протонов Np и электронов Ne, то оно оказывается
заряженным. Заряд тела:
q e( N p N e )
6
7. Свойства электрического заряда
5. Электрический заряд инвариантен: его величина не зависитот системы отсчета, т.е. от того, движется он или покоится:
q inv
7
8. Свойства электрического заряда
6. Электрический заряд подчиняется закону сохраненияэлектрического заряда: алгебраическая сумма электрических
зарядов замкнутой системы остается неизменной, какие бы
процессы не происходили внутри данной системы
N
q qi const
i 1
(под замкнутой системой понимается система, которая не
обменивается зарядами с внешними телами)
8
9. Закон Кулона
Точечные электрические заряды – элементарные частицыили заряженные тела, размеры которых малы по сравнению с
расстоянием между ними.
Закон Кулона. Сила взаимодействия F между двумя
точечными зарядами q1 и q2, находящимися в вакууме, прямо
пропорциональна произведению этих зарядов и обратно
пропорциональна квадрату расстояния r между ними:
1 q1q2
F
4 0 r 2
Величина 0 = 8,85 10-12 Ф/м – электрическая постоянная,
относящаяся к числу фундаментальных физических констант.
9
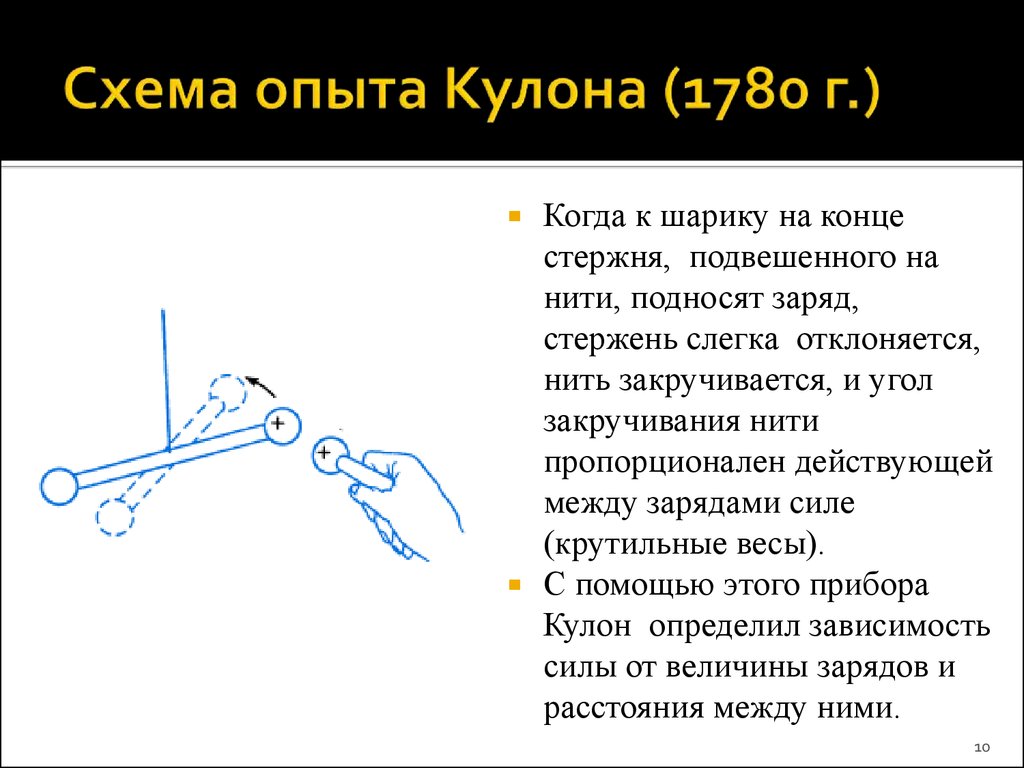
10. Схема опыта Кулона (1780 г.)
Когда к шарику на концестержня, подвешенного на
нити, подносят заряд,
стержень слегка отклоняется,
нить закручивается, и угол
закручивания нити
пропорционален действующей
между зарядами силе
(крутильные весы).
С помощью этого прибора
Кулон определил зависимость
силы от величины зарядов и
расстояния между ними.
10
11. Закон Кулона
Сила F направлена вдоль прямой, соединяющей заряды q1 иq2, т.е. является центральной силой, и соответствует
притяжению, если q1q2 < 0 (заряды разноименные) и
отталкиванию, если q1q2 > 0 (заряды одного знака).
11
12. Закон Кулона в векторной форме
Формула, выражающаязакон Кулона, в векторной
форме: сила F12 ,
действующая на заряд q1 со
стороны заряда q2:
F12
1 q1q2
r12
3
4 0 r12
Здесь r – радиус-вектор,
проведенный из заряда q2 к
заряду q1.
На электрический заряд q2,
согласно третьему закону
Ньютона, действует сила
F21 = –F12.
12
13. Принцип суперпозиции сил
К кулоновским силам применим рассмотренный в механикепринцип суперпозиции сил: результирующая сила,
действующая со стороны нескольких точечных зарядов q1,
q2, …, qi, …, qN, на точечный заряд q, равна векторной сумме
сил, приложенных к нему со стороны каждого из зарядов в
отдельности:
N
F F1 F2 ... FN Fi
i 1
N
N 1 qqi
qi ri
q
F
r
3 i
3
4
4
r
r
i 1
0
0 i 1
i
i
Здесь ri – радиус-вектор, проведенный из заряда q к заряду qi;
ri – расстояние между зарядами q и qi.
13
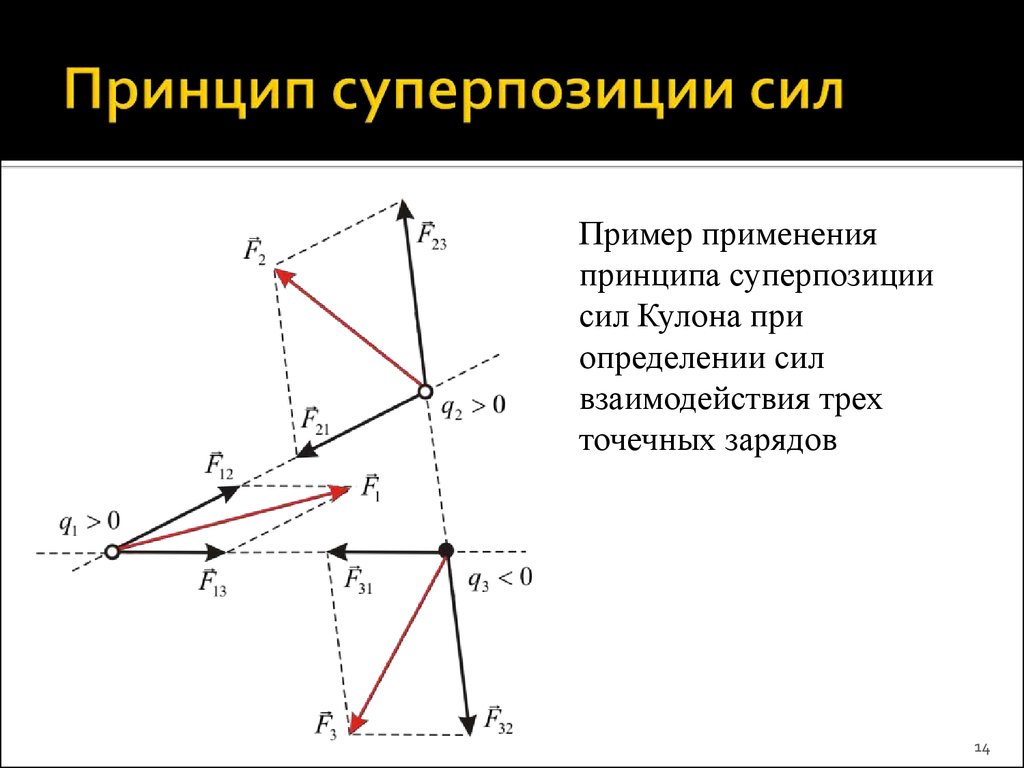
14. Принцип суперпозиции сил
Пример примененияпринципа суперпозиции
сил Кулона при
определении сил
взаимодействия трех
точечных зарядов
14
15. Плотности заряда
Часто бывает значительно удобнее считать, что зарядыраспределены в заряженном теле непрерывно:
вдоль некоторой линии (например, в случае заряженного тонкого
стержня, нити);
по поверхности (например, в случае заряженной пластины, сферы);\
в объеме (например, в случае заряженного шара).
15
16. Плотности заряда
Распределениеэлектрического
заряда q по
пространству
объемом V
Объемная
(пространственная)
плотность заряда
(r), Кл/м3
Распределение
электрического
заряда q по
поверхности
площадью S
Поверхностная
плотность заряда
(r), Кл/м2
dq = dV
dq = dS
Распределение
электрического
заряда q по линии
длины l
Линейная
плотность заряда
(r), Кл/м
dq = dl
16
17. 1.2 Электрическое поле. Напряженность
ЛЕКЦИЯ 1. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ18. Электромагнитное поле
– особый вид материи, посредствомкоторого осуществляется взаимодействие заряженных частиц.
Это означает, что:
заряженные частицы создают в окружающем пространстве
электромагнитное поле;
на заряженную частицу действует электромагнитное поле,
существующее в данной точке пространства и в данный момент
времени.
Поле, создаваемое точечным источником, пропорционально
его заряду; воздействие поля на заряженную частицу
пропорционально заряду этой частицы.
18
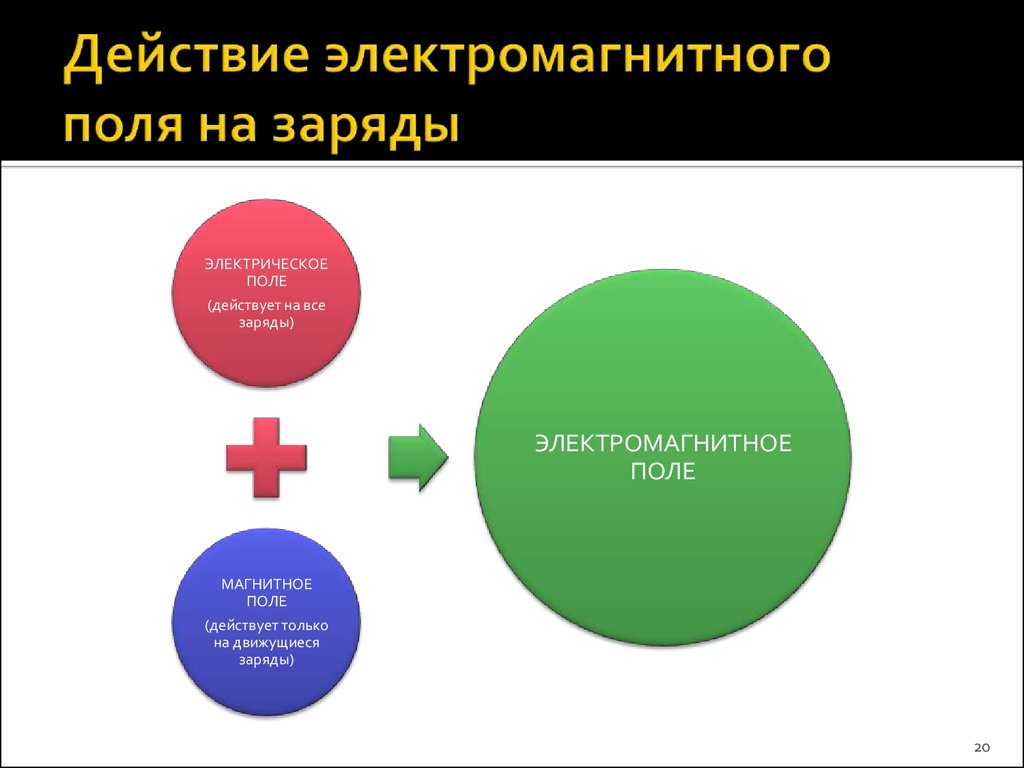
19. Источники электромагнитного поля
Неподвижные зарядыДвижущиеся заряды
Электрическое поле
Электрическое и
магнитное поля
19
20. Действие электромагнитного поля на заряды
ЭЛЕКТРИЧЕСКОЕПОЛЕ
(действует на все
заряды)
ЭЛЕКТРОМАГНИТНОЕ
ПОЛЕ
МАГНИТНОЕ
ПОЛЕ
(действует только
на движущиеся
заряды)
20
21. Пробный заряд
Для определения характеристик электромагнитного поляиспользуется понятие пробного заряда, внесение
которого в исследуемое поле его не искажает (т.е. не
приводит к смещению источников поля). Для этого
величина пробного заряда должна быть достаточно
малой.
Сила, действующая на неподвижный пробный заряд q0,
пропорциональна его величине и определяется только
электрическим полем:
F q0 E
21
22. Напряженность электрического поля
E – векторнаяфизическая величина, определяемая силой, действующей на
единичный положительный заряд q0, помещенный в данную
точку поля:
F
E
q0
Единица напряженности электростатического поля – вольт
на метр (В/м), или ньютон на кулон (Н/Кл).
22
23. Напряженность электрического поля точечного заряда
;Напряженность электростатического поля точечного
заряда q в вакууме в скалярной и векторной формах
соответственно:
1 q
E
4 0 r 2
E
1 q
r
3
4 0 r
Здесь r – радиус-вектор, проведенный в данную точку поля из
заряда q, создающего поле; r – расстояние между зарядом q и
точкой, в которой определяется вектор E.
23
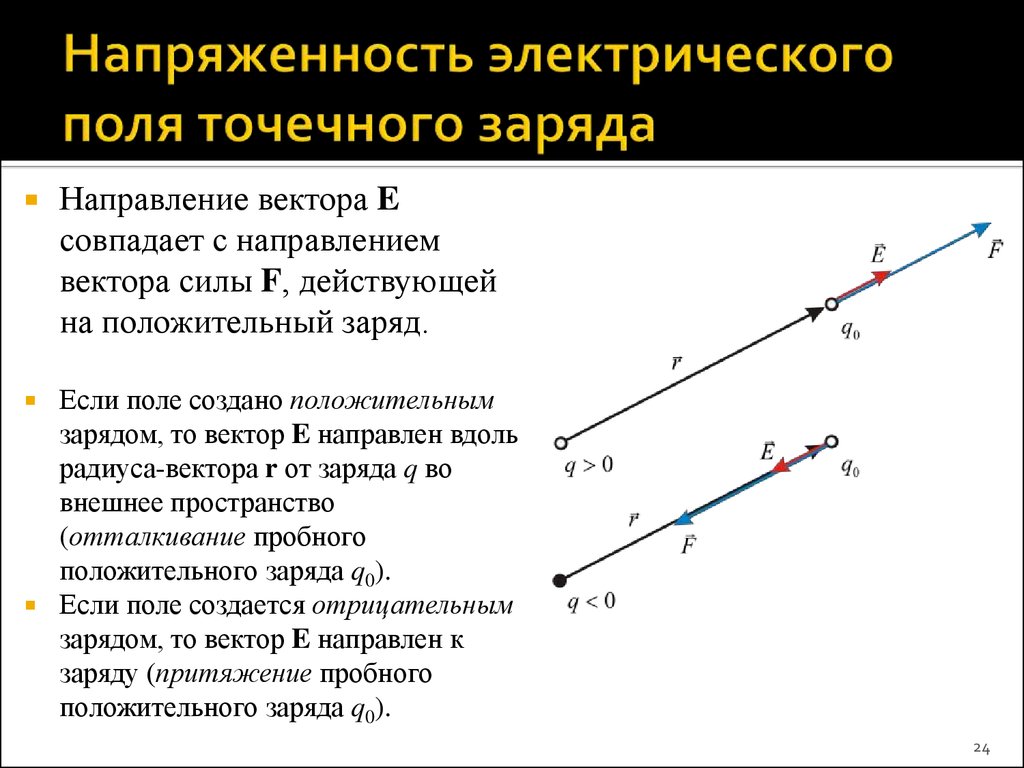
24. Напряженность электрического поля точечного заряда
Направление вектора Eсовпадает с направлением
вектора силы F, действующей
на положительный заряд.
Если поле создано положительным
зарядом, то вектор E направлен вдоль
радиуса-вектора r от заряда q во
внешнее пространство
(отталкивание пробного
положительного заряда q0).
Если поле создается отрицательным
зарядом, то вектор E направлен к
заряду (притяжение пробного
положительного заряда q0).
24
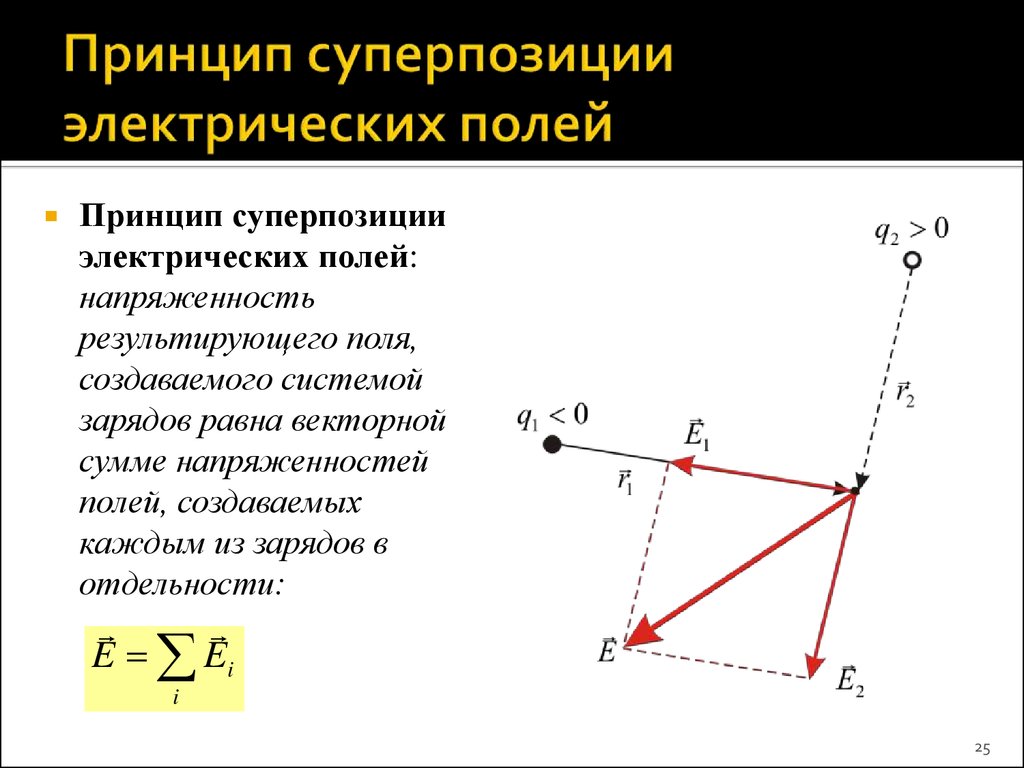
25. Принцип суперпозиции электрических полей
Принцип суперпозицииэлектрических полей:
напряженность
результирующего поля,
создаваемого системой
зарядов равна векторной
сумме напряженностей
полей, создаваемых
каждым из зарядов в
отдельности:
E Ei
i
25
26. Напряженность электрического поля системы точечных зарядов
Из принципа суперпозиции электрических полей следует, чтонапряженность электростатического поля системы
точечных зарядов q1, q2, …, qi, …, qN:
N
E E1 E2 ... E N Ei
i 1
1
4 0
qi
r
3 i
i 1 ri
N
где Ei – напряженность электрического поля, создаваемая
зарядом qi в точке с радиусом-вектором ri, проведенным из
заряда qi; ri – расстояние между зарядом qi и точкой
пространства, в которой вычисляется напряженность Ei поля.
26
27. Напряженность электрического поля пространственно распределенного заряда
Если заряд q распределен в пространстве непрерывно, тонапряженность E электрического поля в данной точке
пространства с радиусом вектором r можно определить
следующим образом:
E dE
1
dq
1
dV
r
r
3
3
4 0 V r
4 0 V r
Т.е. заряженное тело разбивается на части объемом dV,
имеющие заряд dq; далее находится напряженность dE
электрического поля точечного заряда dq в данной точке;
затем с помощью принципа суперпозиции электрических
полей вычисляется напряженность E.
27
28. Напряженность электрического поля заряда, распределенного по поверхности или по линии
Аналогично, для зарядов, распределенных по поверхности Sили длине L заряженных тел:
E
1
dq
1
dS
r
r
3
3
4 0 S r
4 0 S r
E
1
4 0
dq
1
L r 3 r 4 0
dl
L r 3 r
28
29. Силовые линии электрического поля
Графически электростатическое поле изображают с помощьюлиний напряженности (силовых линий) – линий,
касательная к которым в каждой точке совпадает с
направлением вектора E.
Линиям напряженности приписывается направление,
совпадающее с направлением вектора E.
Густота этих линий пропорциональная модулю E вектора
напряженности.
Так как в данной точке пространства вектор E имеет лишь
одно направление, то линии вектора напряженности никогда
не пересекаются.
29
30. Свойства силовых линий электрического поля
1. Силовые линии указывают направление напряженностиэлектрического поля: в любой точке вектор напряженности E
электрического поля направлена по касательной к силовой
линии.
2. Силовые линии проводятся так, чтобы модуль вектора
напряженности электрического поля Е был пропорционален
числу линий, проходящих через единичную площадку,
перпендикулярную линиям.
3. Силовые линии начинаются только на положительных
зарядах и заканчиваются только на отрицательных зарядах;
число линий, выходящих из заряда или входящих в него,
пропорционально величине заряда.
30
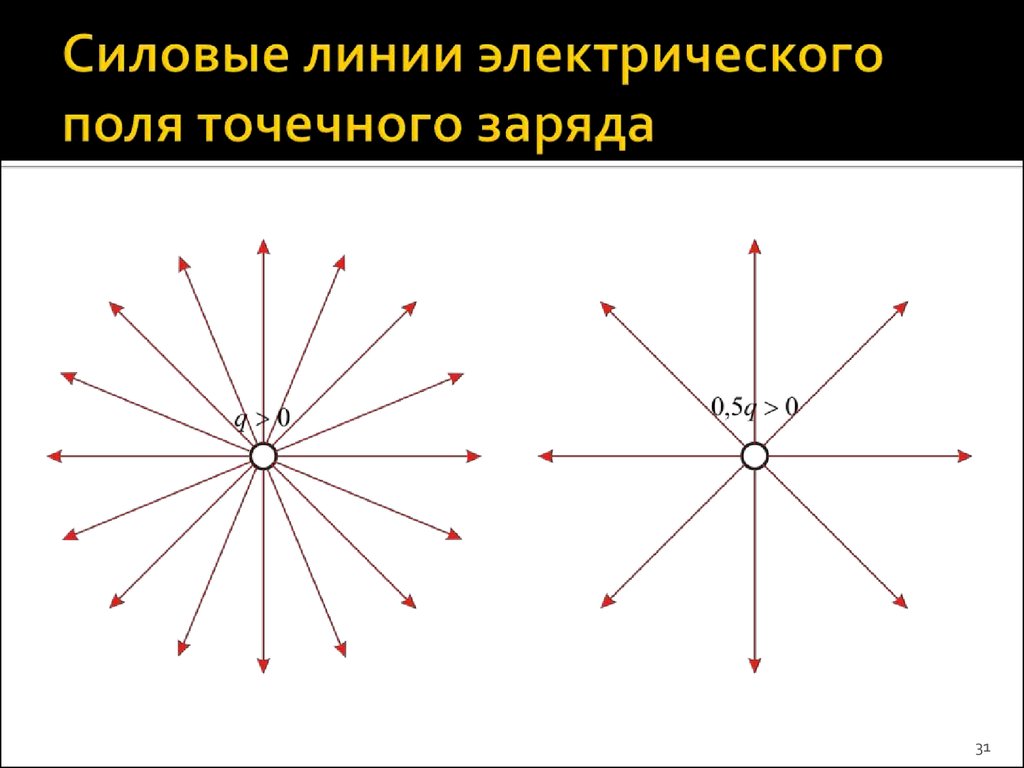
31. Силовые линии электрического поля точечного заряда
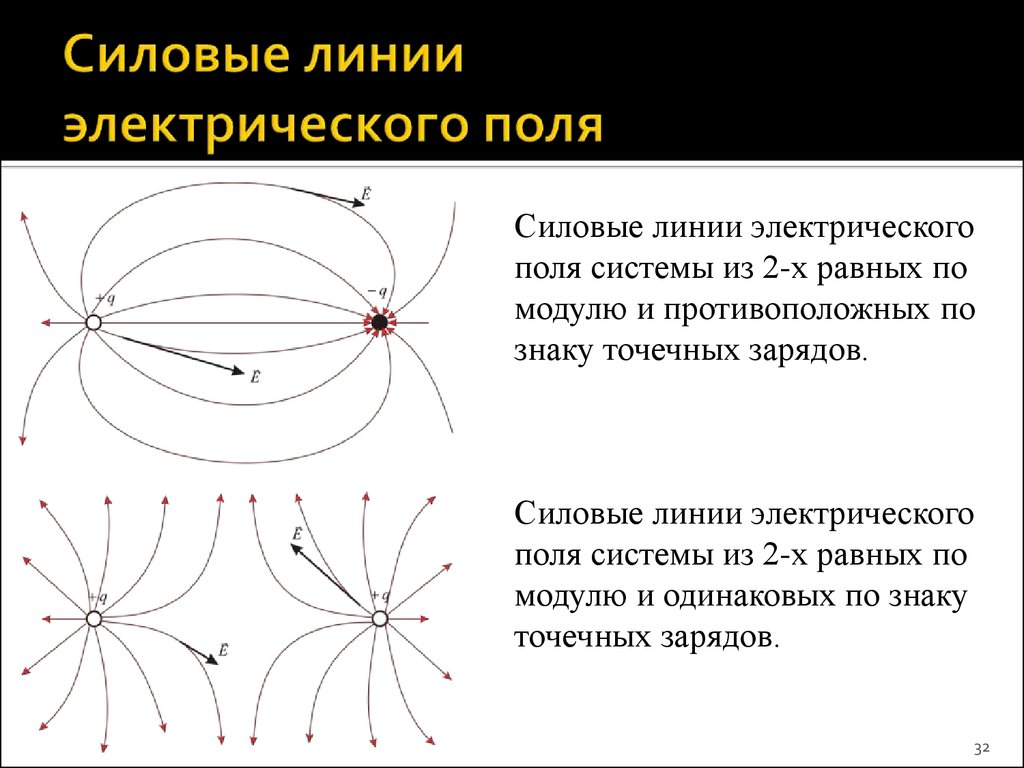
3132. Силовые линии электрического поля
системы из 2-х равных помодулю и противоположных по
знаку точечных зарядов.
Силовые линии электрического
поля системы из 2-х равных по
модулю и одинаковых по знаку
точечных зарядов.
32
33. 1.3 Консервативное электрическое поле
ЛЕКЦИЯ 1. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ34. Консервативное электрическое поле
Как и любое центральное поле, электростатическое полеявляется консервативным (потенциальным).
Это означает, что работа сил поля при перемещении пробного
заряда из точки 1 в точку 2 не зависит от вида траектории
и характера движения заряда.
34
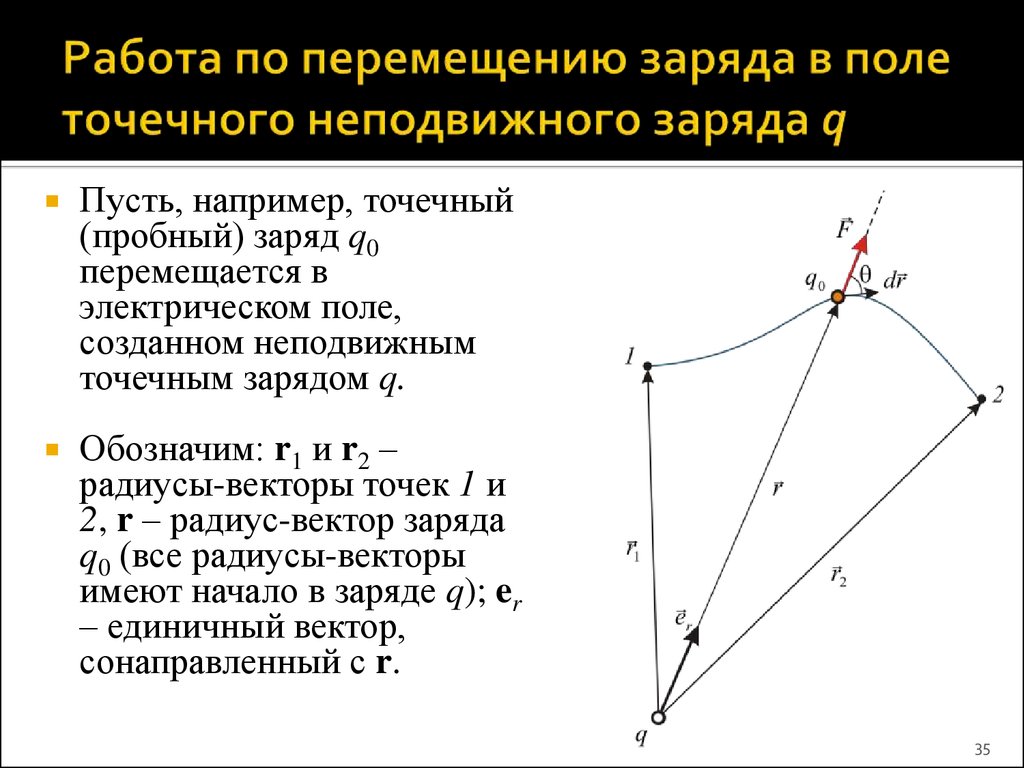
35. Работа по перемещению заряда в поле точечного неподвижного заряда q
Пусть, например, точечный(пробный) заряд q0
перемещается в
электрическом поле,
созданном неподвижным
точечным зарядом q.
Обозначим: r1 и r2 –
радиусы-векторы точек 1 и
2, r – радиус-вектор заряда
q0 (все радиусы-векторы
имеют начало в заряде q); er
– единичный вектор,
сонаправленный с r.
35
36. Работа по перемещению заряда q0 в поле точечного неподвижного заряда q
22 1 q0 q
A F dr
r dr
3
4 0 r
1
1
r
2
q0 q r dr cos q0 q 2 dr
3
2
4 0 1
r
4 0 r1 r
q0 q 1 1
4 0 r1 r2
В консервативном поле работа по
перемещению электрического
заряда вдоль замкнутой
траектории равна нулю: A A 0
L
36
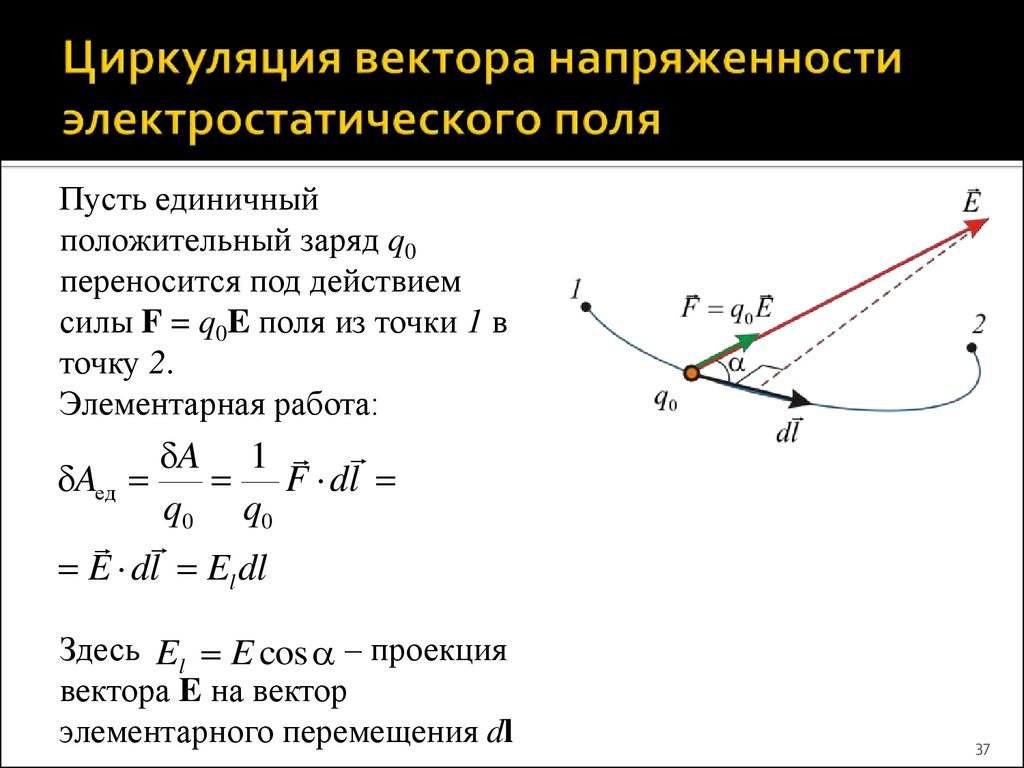
37. Циркуляция вектора напряженности электростатического поля
Пусть единичныйположительный заряд q0
переносится под действием
силы F = q0E поля из точки 1 в
точку 2.
Элементарная работа:
A 1
Aед
F dl
q0 q0
E dl El dl
Здесь El E cos – проекция
вектора E на вектор
элементарного перемещения dl
37
38. Циркуляция вектора напряженности электростатического поля
Предположим теперь, чтоточки 1 и 2 траектории заряда
совпадают, т.е. траектория
представляет собой
замкнутую линию L
(замкнутый контур).
Тогда работа сил поля по
перемещению единичного
положительного заряда по
замкнутому контуру,
называется циркуляцией
вектора E вдоль этого
контура:
Aед Aед E dl
L
L
38
39. Теорема о циркуляции вектора напряженности электростатического поля
Из свойства консервативности электростатического поляследует теорема о циркуляции вектора E: циркуляция
вектора напряженности E электростатического поля вдоль
любого замкнутого контура L равна нулю:
E dl El dl 0
L
L
Силовое поле, обладающее таким свойством, называется
потенциальным.
Последняя формула справедлива только для полей,
созданных неподвижными электрическими зарядами, т.е. для
электростатических полей.
39
40. Потенциальная энергия заряда
В потенциальном поле тела обладают потенциальнойэнергией и работа консервативных сил совершает за счет
убыли потенциальной энергии тел.
Работу консервативной силы Кулона при перемещении
точечного заряда q0 из точки 1 в точку 2 можно представить в
виде разности потенциальных энергий заряда q0 в начальной и
конечной точках: A = –d (для элементарного перемещения),
A12 1 2
С другой стороны, известно, что
q0 q
q0 q
A12
4 0 r1 4 0 r2
40
41. Потенциальная энергия заряда
Таким образом, потенциальная энергия заряда q0 вовнешнем электростатическим поле точечного заряда q равна
q0 q
const
4 0 r
Считая, что при удалении заряда q0 на бесконечность
потенциальная энергия обращается в ноль, получаем:
const = 0, т.е.
q0 q
4 0 r
Для одноименных зарядов, что соответствует отталкиванию,
> 0 (если q0q > 0), для разноименных зарядов (притяжение)
(q0q < 0) < 0.
41
42. Потенциальная энергия заряда q0 в электрическом поле системы точечных зарядов
Если поле создается системой N точечных зарядов, топотенциальная энергия заряда q0, находящегося в этом поле,
равна сумме его потенциальных энергий, создаваемых
каждым из зарядов системы в отдельности в той точке
пространства, где находится заряд q0:
N
q0
i
4 0
i 1
N
qi
i 1 ri
Здесь ri – расстояние между зарядом qi системы и зарядом q0.
42
43. 1.4 Потенциал электрического поля
ЛЕКЦИЯ 1. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ44. Потенциал электростатического поля
Потенциалом электростатического поля в данной точкепространства называется скалярная физическая величина,
численно равная потенциальной энергии единичного
пробного заряда q0, помещенного в данную точку поля:
q0
Например, потенциал поля, созданного точечным зарядом q
в вакууме на расстоянии r от него, равен
q
4 0 r
44
45. Потенциал электростатического поля
Из приведенного примера видно, что отношение /q0 независит от выбора пробного заряда, а характеризуется только
зарядом, создающим поле.
Таким образом, потенциал является скалярной
(энергетической) характеристикой электростатического
поля (напряженность E – векторная (силовая) характеристика
поля).
Единица потенциала – вольт (В).
Один вольт (1 В) есть потенциал такой точки поля, в которой
заряд в 1 Кл обладает потенциальной энергией 1 Дж (1 В =
1Дж/Кл).
45
46. Разность потенциалов
Работа A12, совершаемая силами электрического поля приперемещении заряда q0 из точки 1 в точку 2 может быть
представлена как
A12 1 2 q0 1 2 q0
т.е. она равна произведению перемещаемого заряда q0 на
разность потенциалов в начальной и конечной точках.
46
47. Разность потенциалов
двух точек 1 и 2электростатического поля определяется работой,
совершаемой силами поля, при перемещении единичного
положительного заряда из точки 1 в точку 2:
A12
1 2
q0
47
48. Связь между разностью потенциалов и напряженностью электростатического поля
Пользуясь определением напряженностиэлектростатического поля, выражение для
работы можно переписать в виде:
2
A12 Fdl q 0 Edl
2
откуда
1
1
A12 2 2
1 2
Edl El dl
q0
1
1
Интегрирование может проводиться вдоль любой траектории,
соединяющей начальную и конечную точки, так как работа сил
электростатического поля не зависит от траектории заряда q0.
48
49. Еще одно определение потенциала
Если перемещать заряд q0 из произвольной точки поля запределы поля (на бесконечность), где потенциальная энергия
= 0, а значит и потенциал = /q0 = 0, то работа сил
электростатического поля
A q0 0 q0
откуда
A
q0
Потенциал данной точки поля – физическая величина,
определяемая работой сил электростатического поля по
перемещению единичного положительного заряда из данной
точки в бесконечность.
49
50. Свойства потенциала
1. Потенциал электростатического поля в данной точкепространства является функцией только координат x, y, z
этой точки:
( x, y, z )
50
51. Свойства потенциала
2. Работа сил поля по перемещению единичногоположительного заряда из произвольного начального
положения 1 в произвольное конечное положение 2, равна
убыли потенциала:
Aед E dl 1 2
2
1
Если при этом точки 1 и 2 расположены достаточно близко
друг от друга, то напряженность E электрического поля
можно считать приблизительно одинаковой между точками 1
и 2 и тогда
E dl d
51
52. Свойства потенциала
3. Потенциал электростатического поля определен сточностью до аддитивной постоянной величины.
Это означает, что при замене точки O – начала отсчета
потенциала, на некоторую другую точку O потенциал во
всех точках пространства изменится на одну и ту же
величину C, равную работе сил поля при перемещении
единичного положительного заряда из точки O в точку O :
C ;
O
C E dl
O
52
53. Принцип суперпозиции потенциалов
электростатическихполей: если электрическое поле создано несколькими
зарядами, то потенциал электрического поля системы
зарядов равен алгебраической сумме потенциалов
электрических полей всех этих зарядов:
i
i 1
53
54. Потенциал системы неподвижных точечных зарядов
Например, потенциал точки электрического поля,созданного системой N точечных зарядов q1, q2, …, qi, …, qN
равен:
n
qi
1
4 0
i 1 4 0 ri
N
qi
i 1 ri
Здесь ri – расстояние от данной точки поля до заряда qi
системы.
54
55. Потенциал поля пространственно распределенного заряда
Если заряд q распределен в пространстве с объемнойплотностью , то:
мысленно разделим заряженное тело на элементарные части объемами
dV и зарядами dq;
находим потенциал d электрического поля, созданного в данной точке
зарядом dq по формуле потенциала точечного заряда;
с помощью принципа суперпозиции потенциалов находим потенциал
в данной точке поля:
1
dq
1
dV
4 0 V r
4 0 V r
Здесь r – расстояние между данной точкой поля и
элементарным объемом dV, несущим заряд dq.
55
56. Потенциал поля зарядов, распределенных по поверхности или по линии
Аналогично, для зарядов, распределенных по поверхности Sили длине L заряженных тел потенциал в точке с радиусомвектором r равен соответственно:
1
dq
1
dS
4 0 S r
4 0 S r
1
4 0
dq
1
L r 4 0
dl
L r
56
57. Связь между напряженностью и потенциалом электрического поля
Для консервативного поля связь между консервативной силойF и потенциальной энергией имеет вид:
F grad
Здесь i
j k – оператор градиента
x
y
z
Поскольку F = qE и = q , то
E grad
Знак минус показывает, что вектор напряженности
электростатического поля направлен в сторону убывания
потенциала.
57
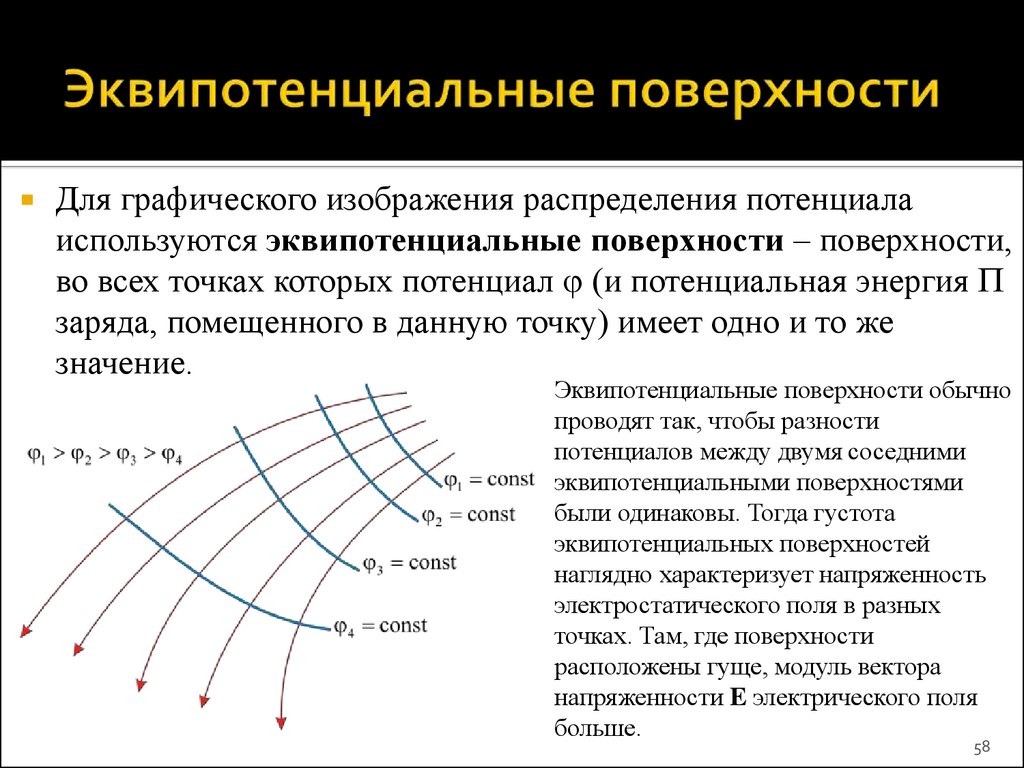
58. Эквипотенциальные поверхности
Для графического изображения распределения потенциалаиспользуются эквипотенциальные поверхности – поверхности,
во всех точках которых потенциал (и потенциальная энергия
заряда, помещенного в данную точку) имеет одно и то же
значение.
Эквипотенциальные поверхности обычно
проводят так, чтобы разности
потенциалов между двумя соседними
эквипотенциальными поверхностями
были одинаковы. Тогда густота
эквипотенциальных поверхностей
наглядно характеризует напряженность
электростатического поля в разных
точках. Там, где поверхности
расположены гуще, модуль вектора
напряженности E электрического поля
больше.
58
59. Эквипотенциальные поверхности
Для точечного зарядаq
4 0 r
поэтому
эквипотенциальные
поверхности представляют
собой концентрические
сферы r = const. С другой
стороны, линии
напряженности E –
радиальные прямые.
59
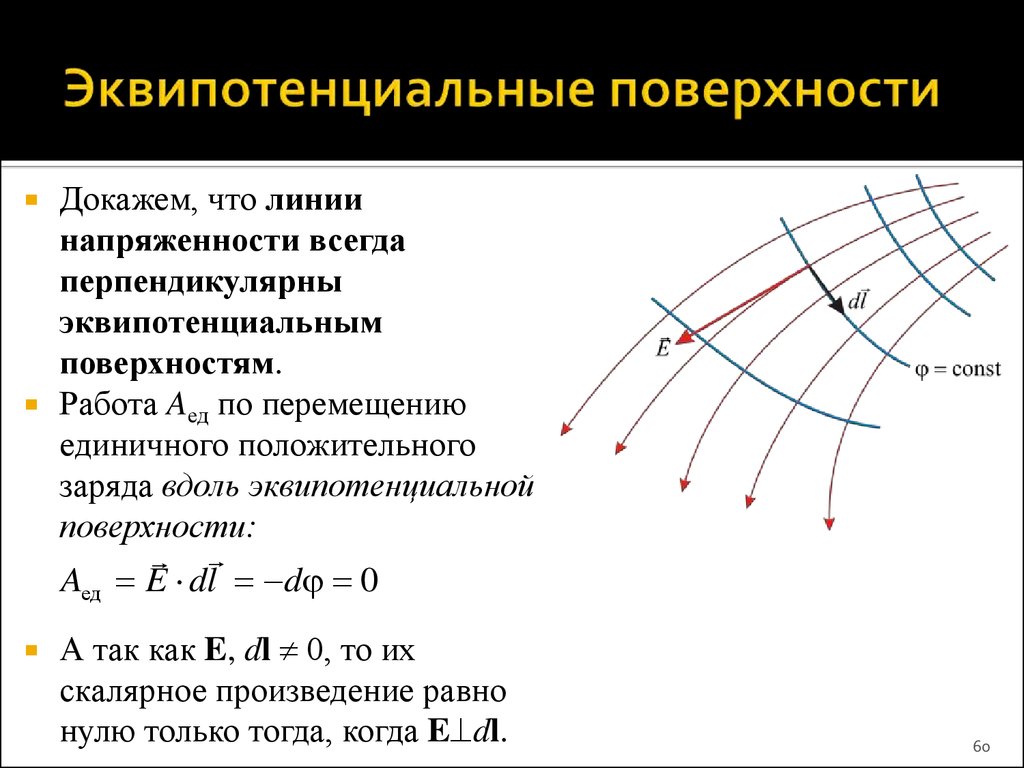
60. Эквипотенциальные поверхности
Докажем, что линиинапряженности всегда
перпендикулярны
эквипотенциальным
поверхностям.
Работа Aед по перемещению
единичного положительного
заряда вдоль эквипотенциальной
поверхности:
Aед E dl d 0
А так как E, dl 0, то их
скалярное произведение равно
нулю только тогда, когда E dl.
60
61. Эквипотенциальные поверхности
На рисунке приведенакартина силовых линий и
эквипотенциальных
поверхностей (обозначены
пунктиром) для системы из
двух одинаковых по
модулю и
противоположных по знаку
точечных зарядов.
61
62. 1.5 Поток вектора напряженности электрического поля. Теорема Гаусса
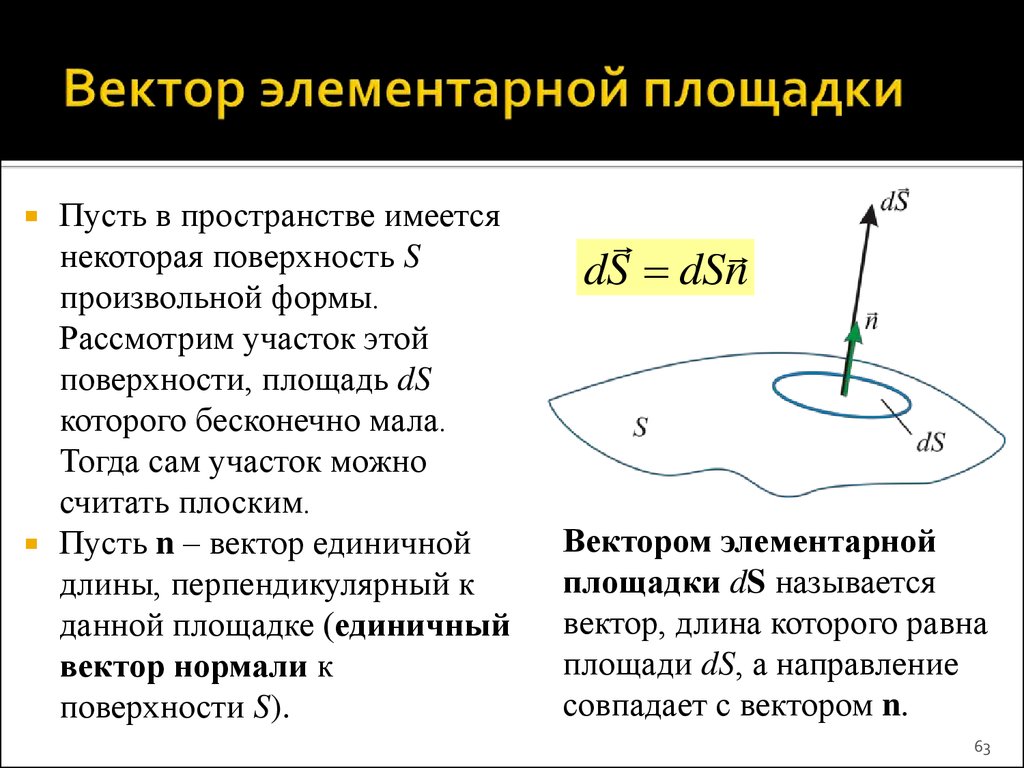
ЛЕКЦИЯ 1. ЭЛЕКТРИЧЕСКОЕ ПЛЕ В ВАКУУМЕ63. Вектор элементарной площадки
Пусть в пространстве имеетсянекоторая поверхность S
произвольной формы.
Рассмотрим участок этой
поверхности, площадь dS
которого бесконечно мала.
Тогда сам участок можно
считать плоским.
Пусть n – вектор единичной
длины, перпендикулярный к
данной площадке (единичный
вектор нормали к
поверхности S).
dS dSn
Вектором элементарной
площадки dS называется
вектор, длина которого равна
площади dS, а направление
совпадает с вектором n.
63
64. Поток вектора напряженности электрического поля
Рассмотрим произвольнуюэлементарную площадку dS в
области пространства, где имеется
электрическое поле.
Ввиду малости dS считаем, что в
любое ее точке E = const.
Выберем единичный вектор нормали
n к площадке. Обозначим – угол
между векторами E и n (dS).
Потоком d вектора напряженности
электрического поля E через
d E dS EdS cos
элементарную площадку называется
скалярное произведение векторов E
и dS.
64
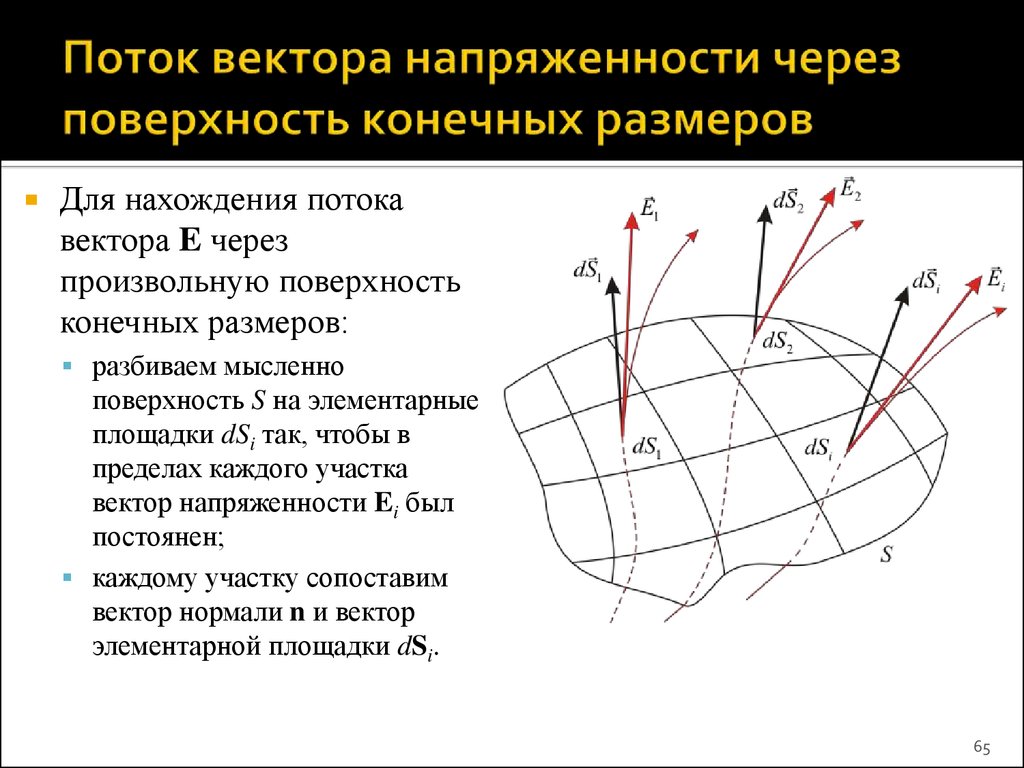
65. Поток вектора напряженности через поверхность конечных размеров
Для нахождения потокавектора E через
произвольную поверхность
конечных размеров:
разбиваем мысленно
поверхность S на элементарные
площадки dSi так, чтобы в
пределах каждого участка
вектор напряженности Ei был
постоянен;
каждому участку сопоставим
вектор нормали n и вектор
элементарной площадки dSi.
65
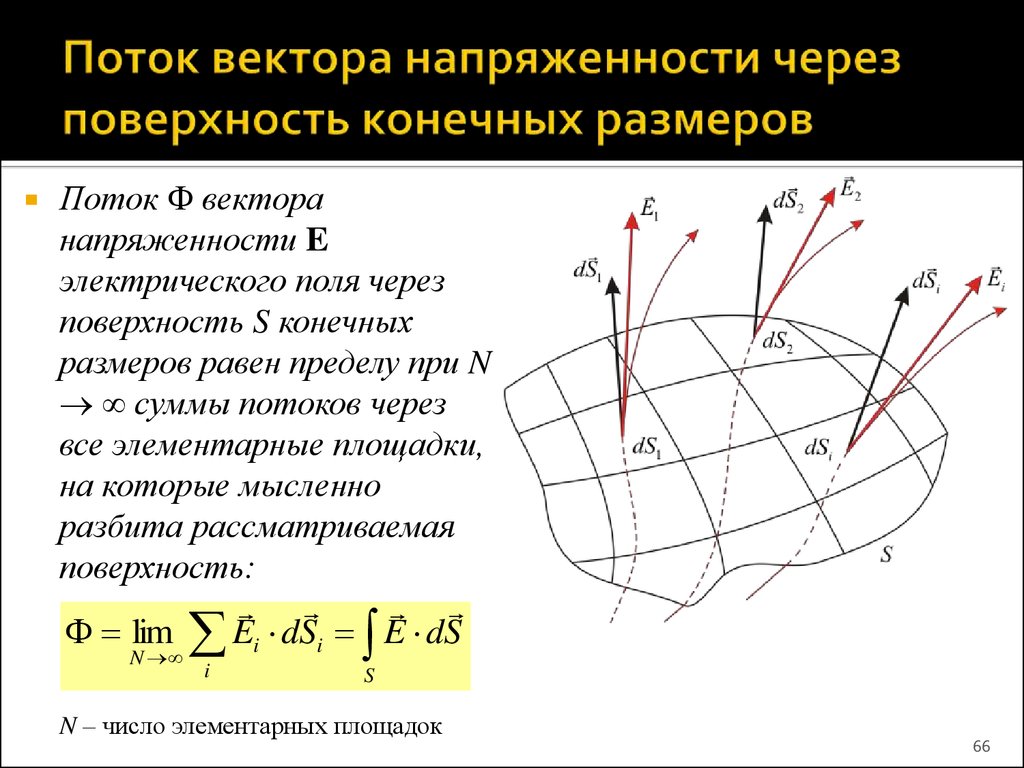
66. Поток вектора напряженности через поверхность конечных размеров
Поток векторанапряженности E
электрического поля через
поверхность S конечных
размеров равен пределу при N
суммы потоков через
все элементарные площадки,
на которые мысленно
разбита рассматриваемая
поверхность:
lim Ei dSi E dS
N
i
S
N – число элементарных площадок
66
67. Поток вектора напряженности через поверхность конечных размеров
Аналогично можноопределить и поток вектора
напряженности через
замкнутую поверхность S.
При этом принято выбирать
внешнюю нормаль к
поверхности:
lim Ei dSi E dS
N
i
S
67
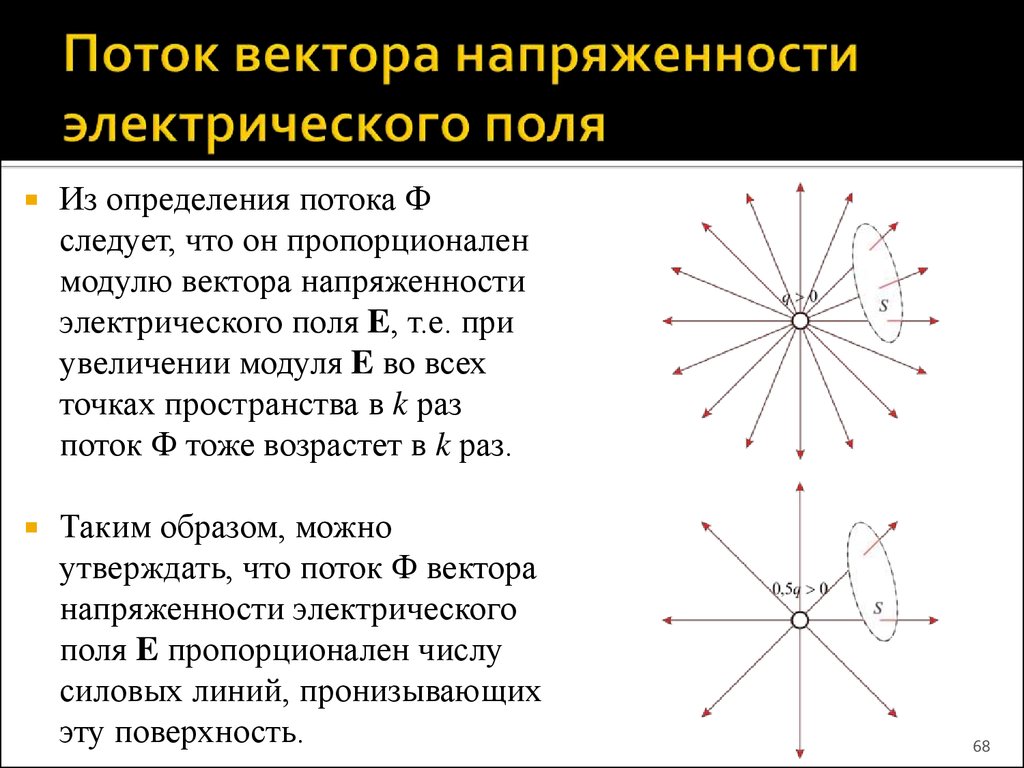
68. Поток вектора напряженности электрического поля
Из определения потокаследует, что он пропорционален
модулю вектора напряженности
электрического поля E, т.е. при
увеличении модуля E во всех
точках пространства в k раз
поток тоже возрастет в k раз.
Таким образом, можно
утверждать, что поток вектора
напряженности электрического
поля E пропорционален числу
силовых линий, пронизывающих
эту поверхность.
68
69. Знак потока
d определяетсяуглом между нормалью n к
элементарной площадке и
вектором напряженности E
электрического поля в этой
же точке.
Из рисунка видно, что поток,
входящий в замкнутый
объем, отрицателен ( < 0),
выходящий из него –
положителен ( > 0).
Таким образом, если число
линий вектора E, входящих в
данный объем и выходящих
из него одинаково, то = 0.
69
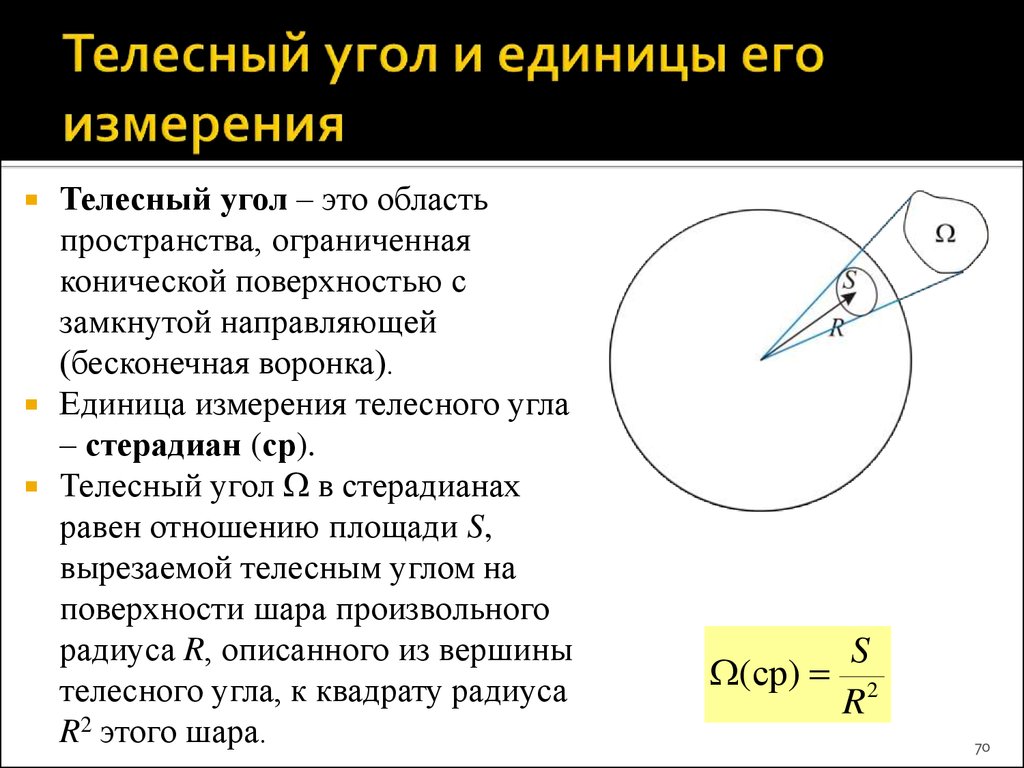
70. Телесный угол и единицы его измерения
Телесный угол – это областьпространства, ограниченная
конической поверхностью с
замкнутой направляющей
(бесконечная воронка).
Единица измерения телесного угла
– стерадиан (ср).
Телесный угол в стерадианах
равен отношению площади S,
вырезаемой телесным углом на
поверхности шара произвольного
радиуса R, описанного из вершины
телесного угла, к квадрату радиуса
R2 этого шара.
S
(ср) 2
R
70
71. Телесный угол и единицы его измерения
Поскольку площадь поверхностишара составляет 4 R2, где R –
радиус шара, то полный
телесный угол в стерадианах
равен
S 4 R 2
(ср) 2 2 4
R
R
71
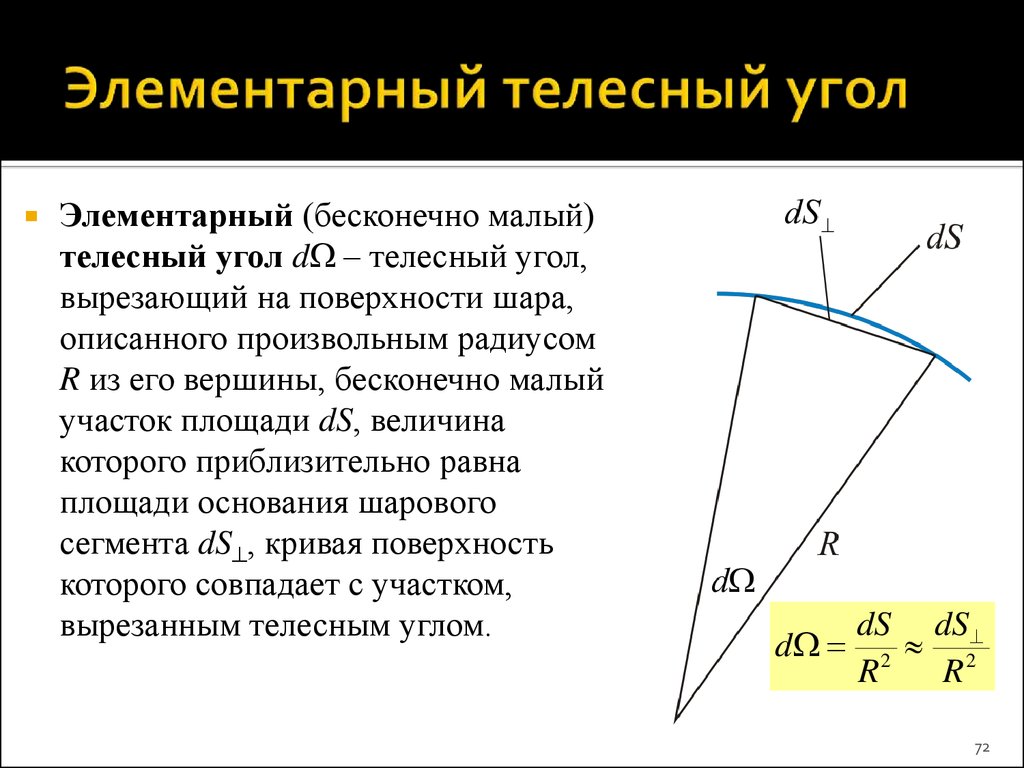
72. Элементарный телесный угол
Элементарный (бесконечно малый)телесный угол d – телесный угол,
вырезающий на поверхности шара,
описанного произвольным радиусом
R из его вершины, бесконечно малый
участок площади dS, величина
которого приблизительно равна
площади основания шарового
сегмента dS , кривая поверхность
которого совпадает с участком,
вырезанным телесным углом.
dS dS
d 2 2
R
R
72
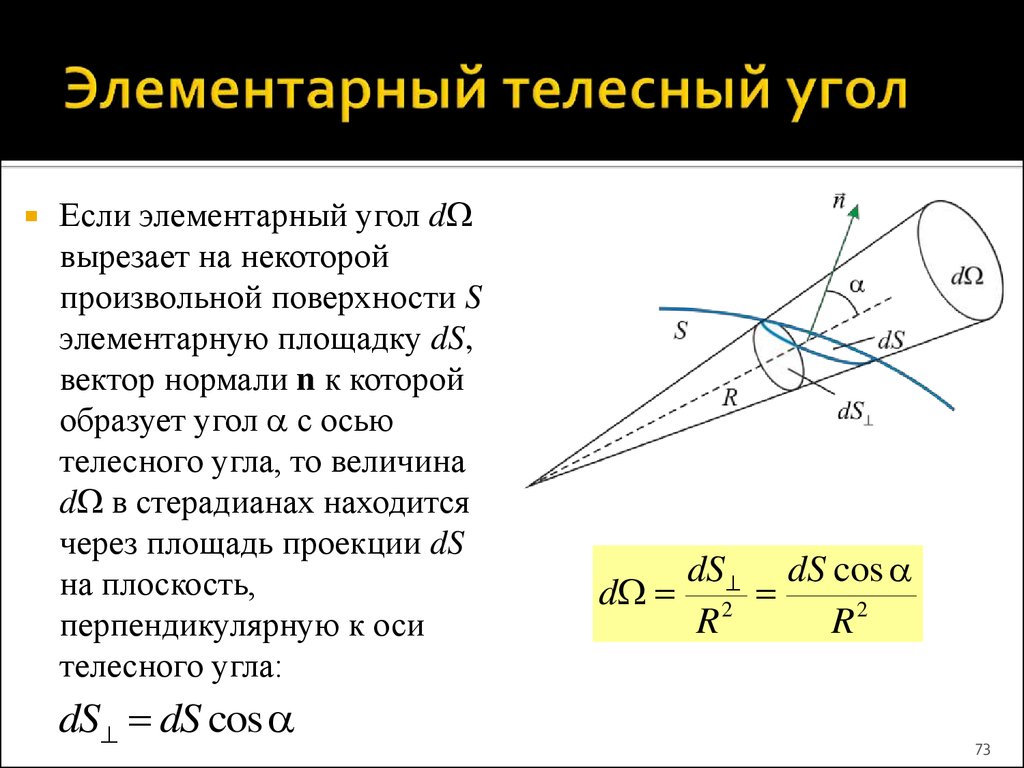
73. Элементарный телесный угол
Если элементарный угол dвырезает на некоторой
произвольной поверхности S
элементарную площадку dS,
вектор нормали n к которой
образует угол с осью
телесного угла, то величина
d в стерадианах находится
через площадь проекции dS
на плоскость,
перпендикулярную к оси
телесного угла:
dS dS cos
dS dS cos
d 2
R
R2
73
74. Теорема Гаусса
является важнейшей теоремойэлектростатики и формулируется следующим образом
Теорема Гаусса: поток вектора напряженности
электрического поля E через произвольную замкнутую
поверхность S равен алгебраической сумме зарядов,
расположенных внутри этой поверхности, деленной на 0:
E dS
S
Докажем ее.
q
i
0
74
75. Теорема Гаусса
Случай 1. Пусть внутриповерхности S расположен
точечный заряд q.
Элементарный поток вектора
E через площадку dS:
d E dS EdS cos
q
q
EdS
dS
d
2
4 0 r
4 0
Тогда поток через поверхность S:
q
q
q
q
d
d
d
4
4 0
4 0 S
4 0
0
S
S
75
76. Теорема Гаусса
Случай 2. Пусть внутри поверхности S расположены точечныезаряды или заряд, непрерывно распределенный в пространстве.
Для потока вектора Ei каждого из зарядов qi через поверхность
S справедлива теорема Гаусса (см. случай 1):
qi
S Ei dSi 0
Сложим подобные равенства для всех зарядов системы и
применим принцип суперпозиции:
qi
qi
qi
i
i
E
d
S
E
d
S
E
d
S
i i i i i i
0
0
0
S
S
S
76
77. Теорема Гаусса
Случай 3. Пусть заряд q расположен вне замкнутой поверхностиS (снаружи).
Разделим мысленно поверхность S на элементарные участки dSi
с помощью телесных углов d , причем каждый из d , вырезает
на поверхности S две элементарные площадки dS1 и dS2.
77
78. Теорема Гаусса
Элементарный поток вектора E через эти площадки:d E1dS1 E2 dS 2 E1dS1 cos 1 E2 dS 2 cos( 2 )
q
q
q dS1 dS 2
2 2
dS1
dS 2
2
2
4 0 r1
4 0 r2
4 0 r1
r2
q
(d d ) 0
4 0
Суммируя все элементарные
потоки, получаем, что поток
вектора напряженности
электрического поля E через
поверхность, не
охватывающую заряды,
равен нулю.
78
79. 1.6 Применение теоремы Гаусса для расчета электрических полей
ЛЕКЦИЯ 1. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ80. Общие правила использования теоремы Гаусса для расчета электрических полей
Основные затруднения при использовании теоремы Гауссасвязаны с выбором замкнутой поверхности S. Чтобы их
избежать, необходимо придерживаться следующих
рекомендаций:
Из соображений симметрии находят направление вектора E в пространстве,
окружающем заряженное тело.
Точка, в которой определяют вектор напряженности E, должна
принадлежать замкнутой поверхности интегрирования S.
Поверхность S выбирают симметричной расположению зарядов, а ее
составные части должны быть либо перпендикулярны, либо касательные к
вектору напряженности. В этом случае поток вектора напряженности
представляется в виде суммы потоков, один из которых равен нулю в силу
перпендикулярности векторов E и dS , а другой – равен 0 (т.к. в любой
точке поверхности En = const) в зависимости от взаимного направления
нормали к поверхности и вектора .
80
81. 1.6 Применение теоремы Гаусса для расчета электрических полей
1.6.1 ЭЛЕКТРИЧЕСКОЕ ПОЛЕ РАВНОМЕРНО ЗАРЯЖЕННОЙ СФЕРЫ81
82. Постановка задачи
Рассмотрим сферическуюповерхность радиусом R, по
которой равномерно распределен
положительный заряд q = S, где
– поверхностная плотность заряда,
S = 4 R2 – площадь сферы.
Определим с помощью теоремы
Гаусса напряженность E и
потенциал электрического поля в
точках, расположенных снаружи,
внутри и на поверхности сферы.
82
83. Напряженность электрического поля вне сферы
Найдем с помощью теоремы Гауссанапряженность электрического поля
в точках, находящихся на
расстоянии r > R.
Для этого выберем в качестве
поверхности Sr интегрирования
сферическую поверхность радиуса
r, концентрическую к сфере:
q
2
S E dS S EdS E S dS E 4 r 0
r
r
r
q
E (r R)
4 0 r 2
83
84. Напряженность электрического поля внутри сферы
Найдем с помощью теоремы Гауссанапряженность электрического поля
в точках, находящихся на
расстоянии r < R (внутри сферы).
Для этого снова выберем в качестве
поверхности Sr интегрирования
сферическую поверхность радиуса
E (r R) 0
r, концентрическую к сфере:
2
E
d
S
EdS
E
dS
E
4
r
0 Следовательно,
S
S
S
напряженность E
r
r
r
электрического поля
(т.к. выбранная поверхность не
внутри заряженной
охватывает заряда).
сферы равна нулю.
84
85. Напряженность электрического поля заряженной сферы
Таким образом,напряженность
электрического поля
заряженной сферы:
q
R 2
, r R;
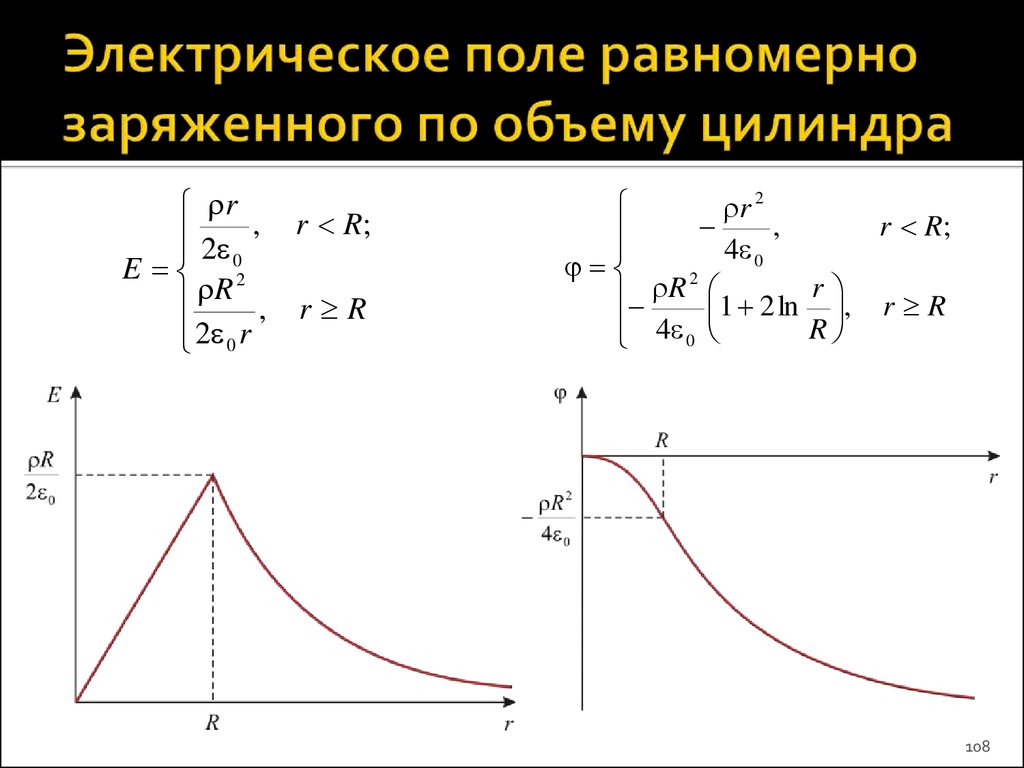
2
2
E 4 0 r
0r
0,
r R.
Поле равномерно заряженной сферы вне этой поверхности
совпадает с полем точечного заряда, а внутри поверхности
поле равно нулю.
85
86. Потенциал электрического поля вне заряженной сферы
Разность потенциалов между двумя точками, находящихся нарасстояниях r1 и r2 от центра сферы (r1, r2 > R) вне ее, равна
2
r2
q
q
1 2 E (r R)dr
dr
2
4 0
1
r1 4 0 r
1 1
r1 r2
Если r1 = r > R, r2 = , то получаем, что потенциал (r > R)
заряженной сферы в точке, находящейся на расстоянии r от ее
центра:
q
R 2
r R
4 0 r 0 r
86
87. Потенциал электрического поля внутри заряженной сферы
Внутри заряженной сферы поля нет и потенциал в любойточке внутри ее равен потенциалу на ее поверхности (r < R)
= const = (R):
q
R
r R
4 0 R 0
87
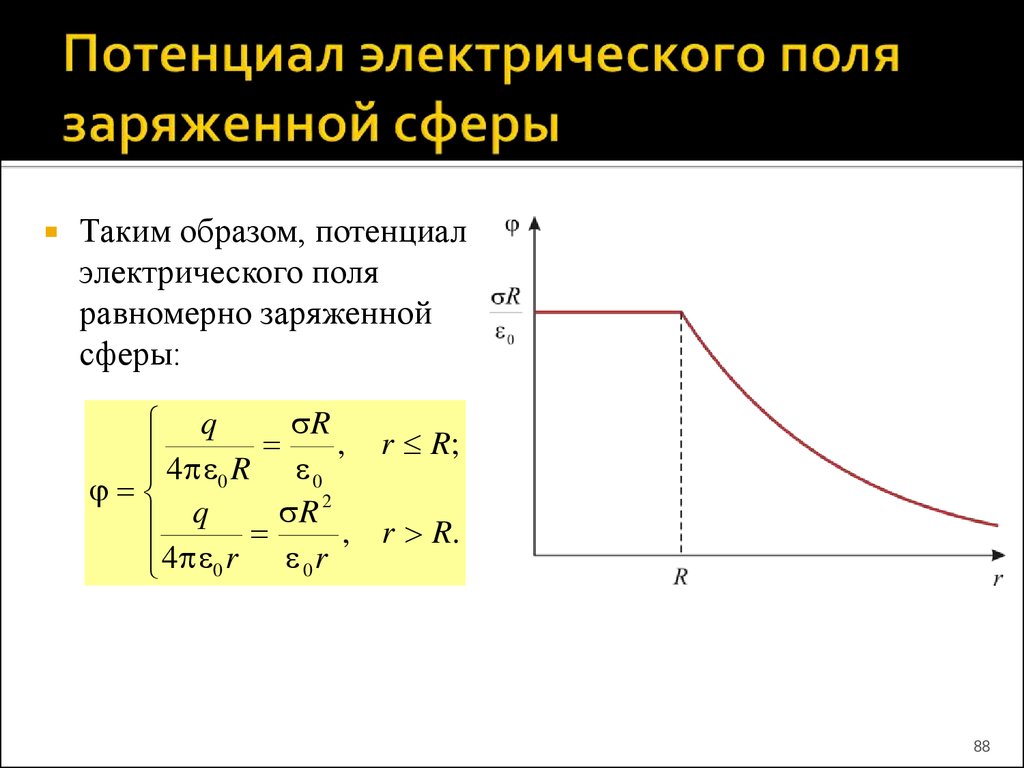
88. Потенциал электрического поля заряженной сферы
Таким образом, потенциалэлектрического поля
равномерно заряженной
сферы:
R
q
4 R , r R;
0
0
2
q
R
, r R.
4 0 r 0 r
88
89. 1.6 Применение теоремы Гаусса для расчета электрических полей
1.6.2 ЭЛЕКТРИЧЕСКОЕ ПОЛЕ РАВНОМЕРНО ЗАРЯЖЕННОГО ШАРА89
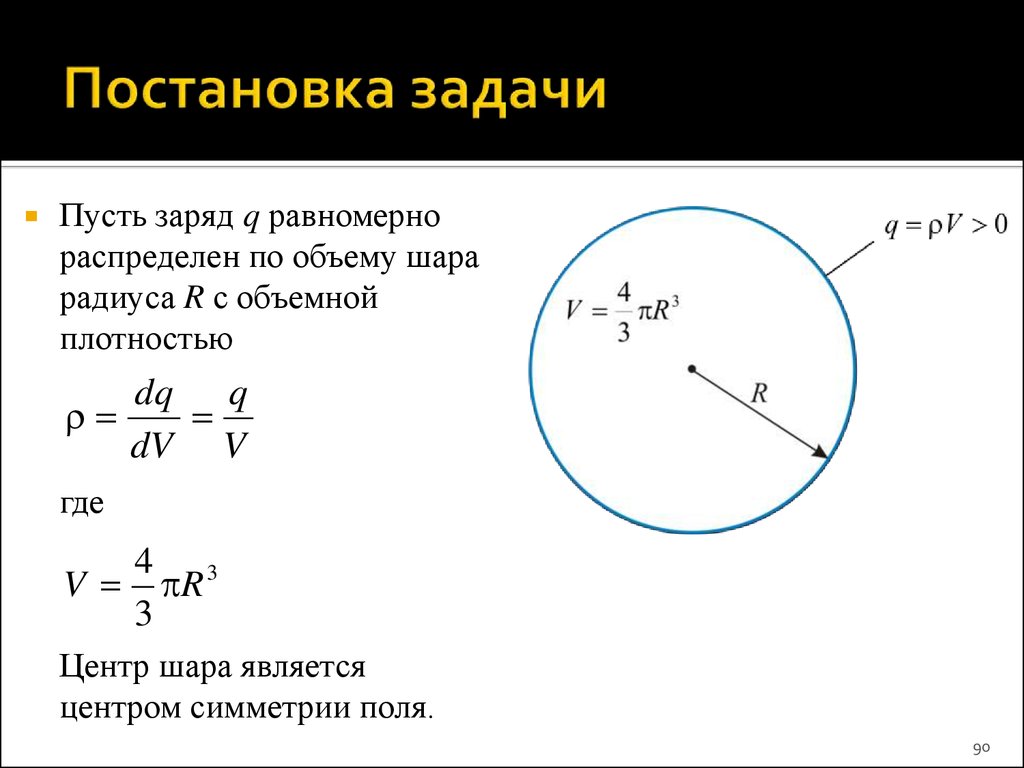
90. Постановка задачи
Пусть заряд q равномернораспределен по объему шара
радиуса R с объемной
плотностью
dq q
dV V
где
4 3
V R
3
Центр шара является
центром симметрии поля.
90
91. Электрическое поле вне равномерно заряженного шара
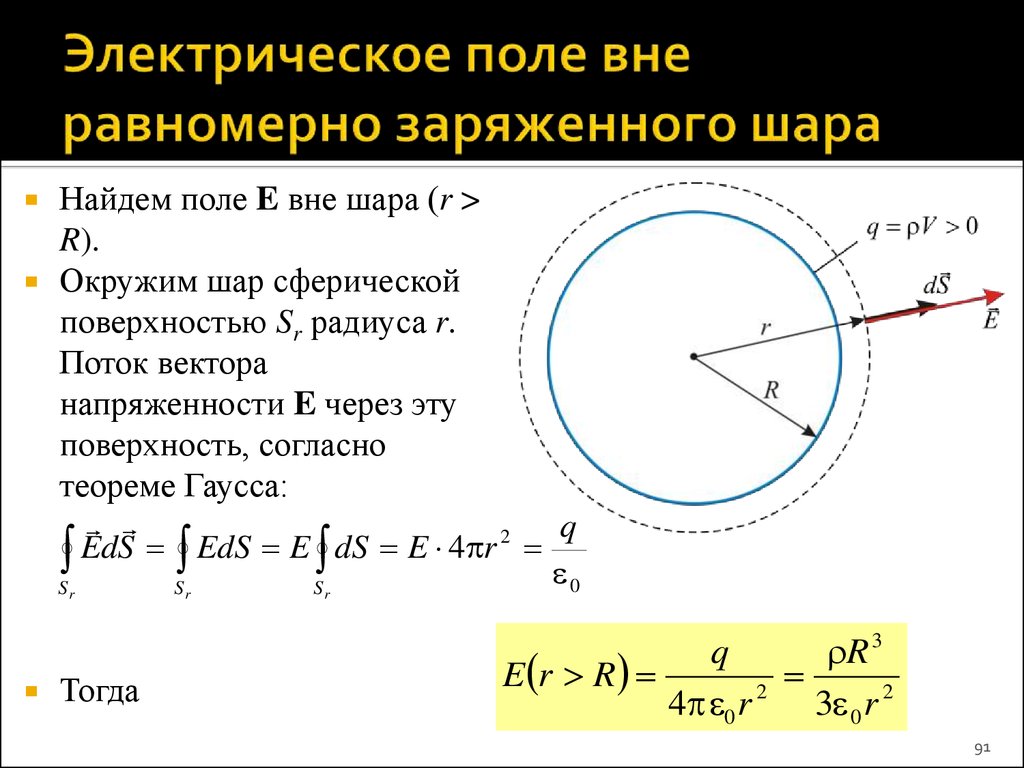
Найдем поле E вне шара (r >R).
Окружим шар сферической
поверхностью Sr радиуса r.
Поток вектора
напряженности E через эту
поверхность, согласно
теореме Гаусса:
q
2
S EdS S EdS E S dS E 4 r 0
r
r
r
Тогда
q
R 3
E r R
2
4 0 r
3 0 r 2
91
92. Электрическое поле внутри равномерно заряженного шара
Теперь найдем поле E внутришара (r < R). Проведем
сферическую поверхность Sr
радиуса r. Заряд внутри этой
поверхности:
q
r
q V V q
V
R
3
Тогда, по теореме Гаусса:
3
q
q
r
2
E
d
S
EdS
E
dS
E
4
r
S
S
S
0 0 R
r
r
r
q
R
qr
r
E R
E (r R)
2
3
3 0
4 0 R
4 0 R
3 0
92
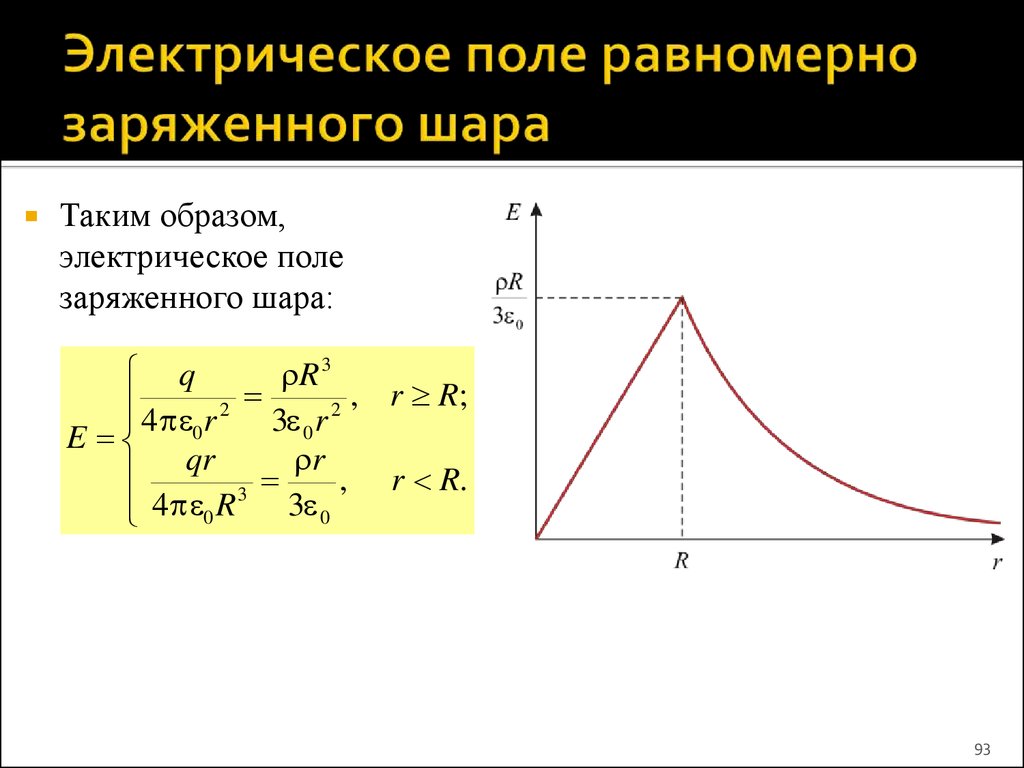
93. Электрическое поле равномерно заряженного шара
Таким образом,электрическое поле
заряженного шара:
q
R 3
4 r 2 3 r 2 , r R;
0
0
E
qr 3 r , r R.
4 0 R
3 0
93
94. Потенциал электрического поля вне равномерно заряженного шара
Разность потенциалов между двумя точками, находящимися нарасстояниях r1 и r2 от центра шара (обе точки находятся вне
шара: r1, r2 > R):
2
r2
q
q
1 2 E (r R)dr
dr
4 0 r2
4 0
1
r1
1 1
r1 r2
Если положить r1 = r и r2 = , то получаем, что потенциал в
точке на расстоянии r от центра шара (вне его) равен
q
R 3
r R
4 0 r 3 0 r
q
R 2
R
4 0 R 3 0
94
95. Потенциал электрического поля внутри равномерно заряженного шара
Для точек, лежащих на расстоянии r внутри шара (r < R)имеем:
qr
q
2
2
1 2 E r R dr
r
r
1
3
3 2
4 0 R
8 0 R
1
r1
r2
2
Если, например, r2 = R, r1 = r < R, то
2
2
q
q
q
qr
q
r
2
2
3 2
r R R
R r
3
3
4 0 R 8 0 R 8 0 R
8 0 R
8 0 R
R
Таким образом, потенциал электрического поля внутри шара
q
r 2 R 2
3 2
r R
8 0 R
R 6 0
r2
3 2
R
95
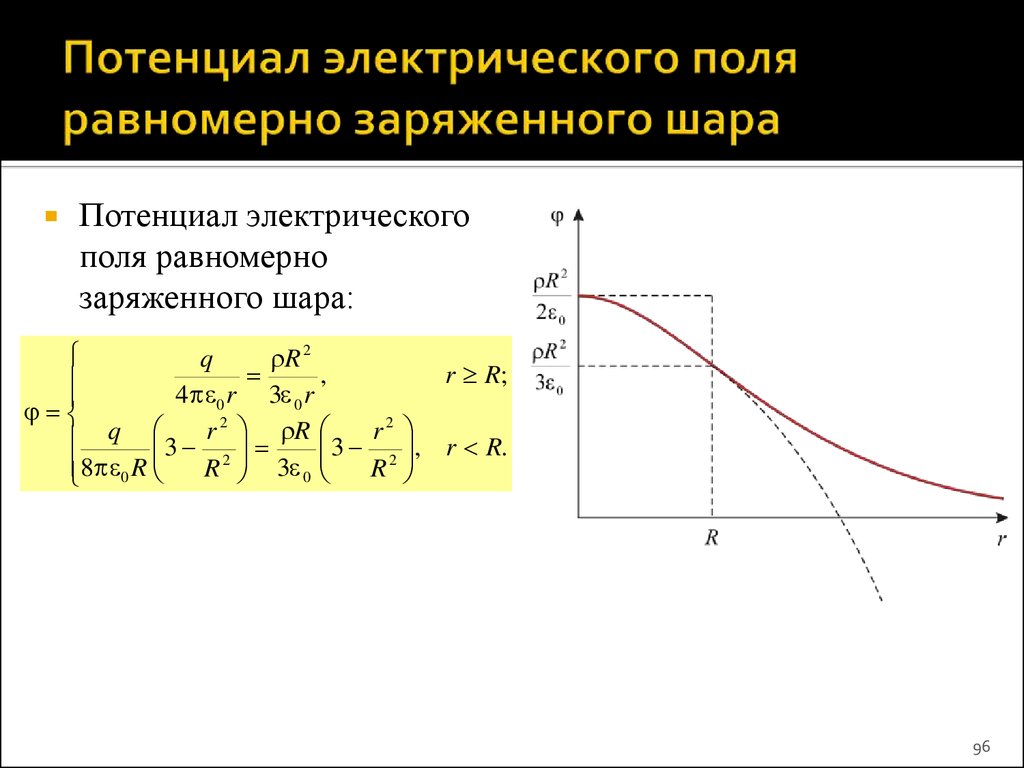
96. Потенциал электрического поля равномерно заряженного шара
Потенциал электрическогополя равномерно
заряженного шара:
q
R 2
,
r R;
4
r
3
r
0
0
2
2
q
r
R
r
3 2
3 2 , r R.
8 0 R
R 3 0
R
96
97. 1.6 Применение теоремы Гаусса для расчета электрических полей
1.6.3 ЭЛЕКТРИЧЕСКОЕ ПОЛЕ РАВНОМЕРНО ЗАРЯЖЕННОЙ НИТИ(ТОНКОГО ЦИЛИНДРА)
97
98. Постановка задачи
Пусть бесконечный цилиндррадиуса R заряжен равномерно с
линейной плотностью заряда > 0.
Линии напряженности
электрического поля E будут
направлены по радиусам круговых
сечений цилиндра с одинаковой
густотой во все стороны
относительно оси цилиндра.
98
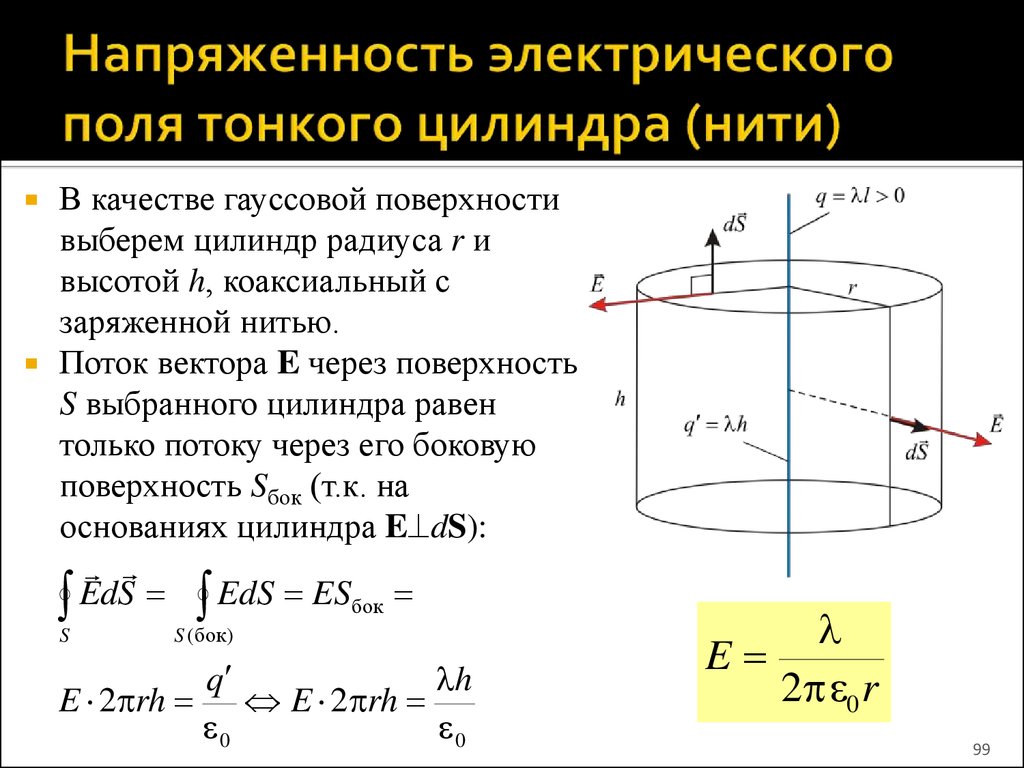
99. Напряженность электрического поля тонкого цилиндра (нити)
В качестве гауссовой поверхностивыберем цилиндр радиуса r и
высотой h, коаксиальный с
заряженной нитью.
Поток вектора E через поверхность
S выбранного цилиндра равен
только потоку через его боковую
поверхность Sбок (т.к. на
основаниях цилиндра E dS):
EdS EdS ESбок
S
S ( бок)
q
h
E 2 rh E 2 rh
0
0
E
2 0 r
99
100. Потенциал электрического поля тонкого цилиндра (нити)
Разность потенциалов между двумя точками поля, находящимисяна расстояниях r1 и r2 от оси цилиндра (нити):
r2
dr
1 2 E (r )dr
ln
2 0 r 2 0 r1
1
r1
2
r2
Если r1 = R (радиус цилиндра), r2 = r, то
r
( R) (r )
ln
2 0 R
И если принять потенциал на поверхности цилиндра (на оси
нити) равным нулю: (R) = 0, потенциал электростатического
поля на расстоянии r от оси цилиндра вне его пределов:
r R
r
ln
2 0 R
100
101. Электрическое поле тонкого цилиндра (нити)
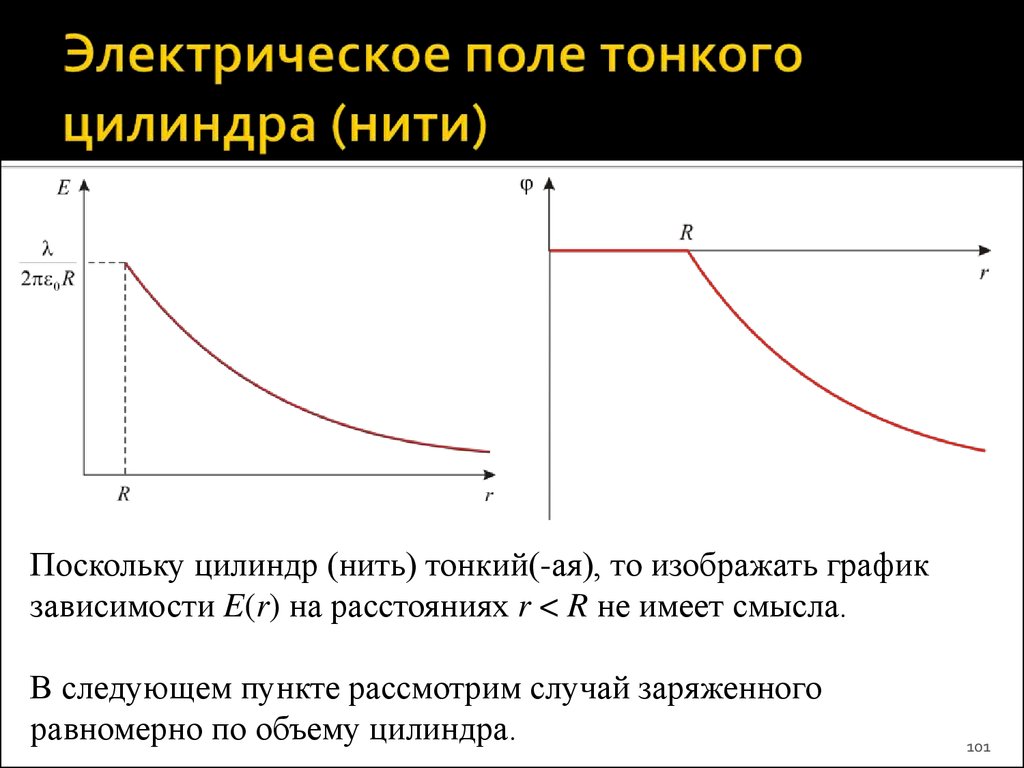
Поскольку цилиндр (нить) тонкий(-ая), то изображать графикзависимости E(r) на расстояниях r < R не имеет смысла.
В следующем пункте рассмотрим случай заряженного
равномерно по объему цилиндра.
101
102. 1.6 Применение теоремы Гаусса для расчета электрических полей
1.6.4 ЭЛЕКТРИЧЕСКОЕ ПОЛЕ РАВНОМЕРНО ЗАРЯЖЕННОГО ПООБЪЕМУ ЦИЛИНДРА
102
103. Постановка задачи
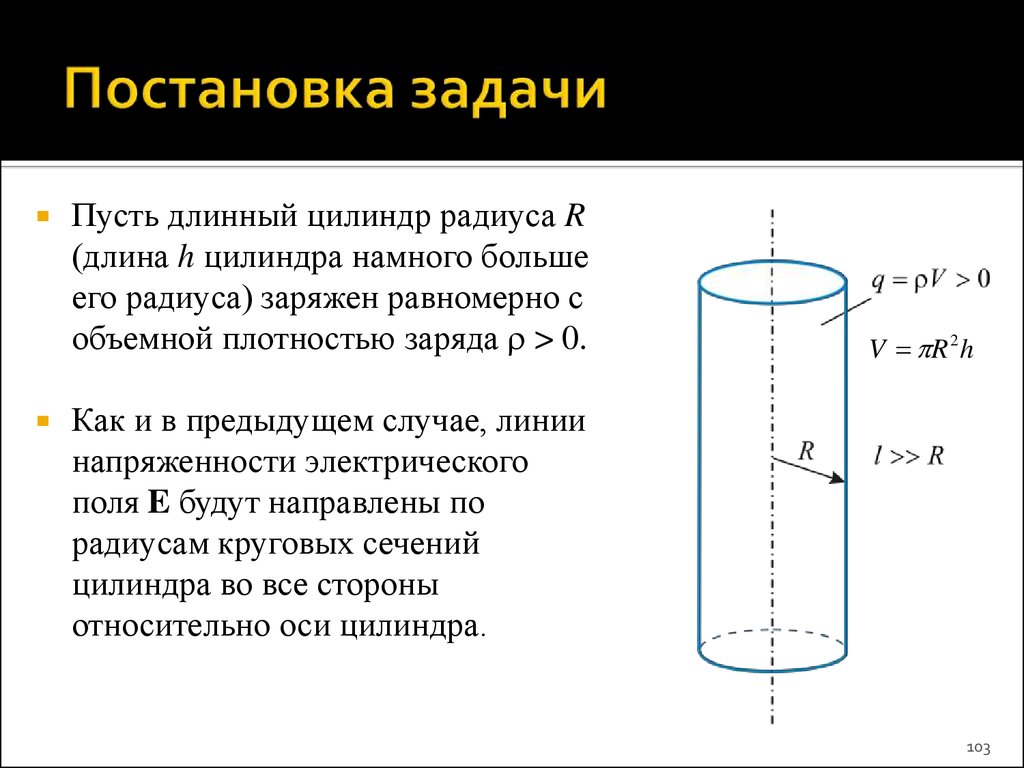
Пусть длинный цилиндр радиуса R(длина h цилиндра намного больше
его радиуса) заряжен равномерно с
объемной плотностью заряда > 0.
V R 2 h
Как и в предыдущем случае, линии
напряженности электрического
поля E будут направлены по
радиусам круговых сечений
цилиндра во все стороны
относительно оси цилиндра.
103
104. Напряженность электрического поля вне цилиндра
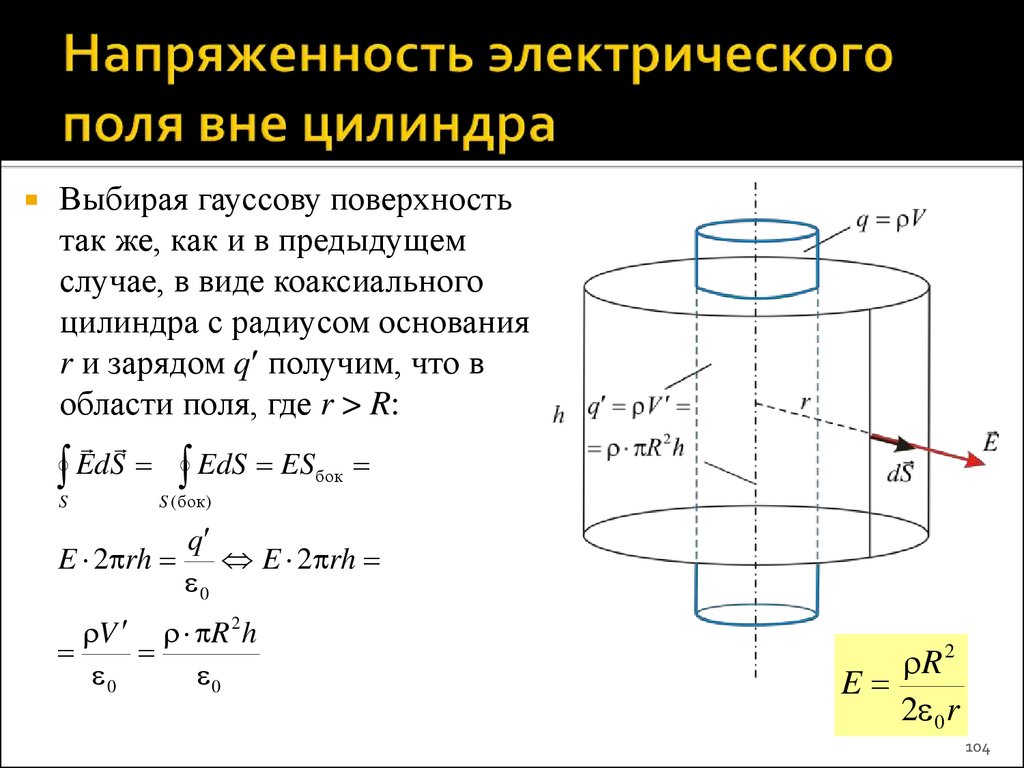
Выбирая гауссову поверхностьтак же, как и в предыдущем
случае, в виде коаксиального
цилиндра с радиусом основания
r и зарядом q получим, что в
области поля, где r > R:
EdS
S
EdS ES
бок
S ( бок)
E 2 rh
q
E 2 rh
0
V R 2 h
0
0
R 2
E
2 0 r
104
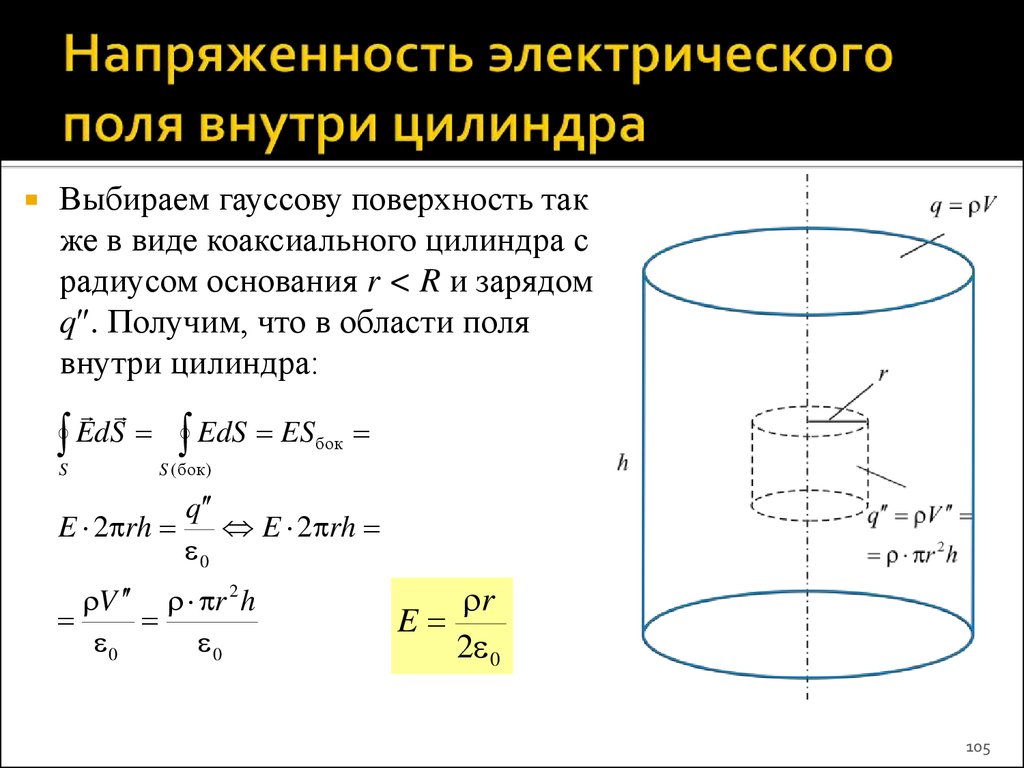
105. Напряженность электрического поля внутри цилиндра
Выбираем гауссову поверхность также в виде коаксиального цилиндра с
радиусом основания r < R и зарядом
q . Получим, что в области поля
внутри цилиндра:
EdS
S
EdS ES
бок
S ( бок)
q
E 2 rh E 2 rh
0
V r 2 h
0
0
E
r
2 0
105
106. Потенциал электрического поля внутри цилиндра
Пусть потенциал на оси цилиндра равен нулю: (r = 0) = 0. Тогдаразность потенциалов между осью цилиндра и точной,
находящейся от оси на расстоянии r < R:
r
r 2
(r 0) (r R) 0 (r R) E (r R)dr
dr
2 0
4 0
1
0
2
r
Тогда потенциал внутри цилиндра на расстоянии r от его оси:
r 2
(r R)
4 0
Потенциал на поверхности цилиндра:
R 2
(r R)
4 0
106
107. Потенциал электрического поля вне цилиндра
Теперь найдем потенциал в точке, находящейся на расстоянии r> R от оси цилиндра (снаружи цилиндра). Для этого найдем
разность потенциалов между этой точной и точкой на
поверхности цилиндра:
r
( R) (r R) E (r R)dr
R
r
(r R) ( R) E (r R)dr
R
R 2 R 2 dr
R 2
r
1 2 ln
4 0 2 0 R r
4 0
R
r
107
108. Электрическое поле равномерно заряженного по объему цилиндра
r2 , r R;
E 02
R , r R
2 0 r
r 2
,
r R;
4 0
2
R
r
1 2 ln , r R
4 0
R
108
109. 1.6 Применение теоремы Гаусса для расчета электрических полей
1.6.4 ЭЛЕКТРИЧЕСКОЕ ПОЛЕ РАВНОМЕРНО ЗАРЯЖЕННОЙБЕСКОНЕЧНОЙ ПЛОСКОСТИ
109
110. Постановка задачи
Пусть бесконечно большаяплоскость x = 0 равномерно
заряжена с поверхностной
плотностью .
Линии вектора
напряженности
электрического поля E
направлены
перпендикулярной к ней от
нее (если > 0) или к ней
(если < 0).
Найдем поле заряженной
плоскости.
110
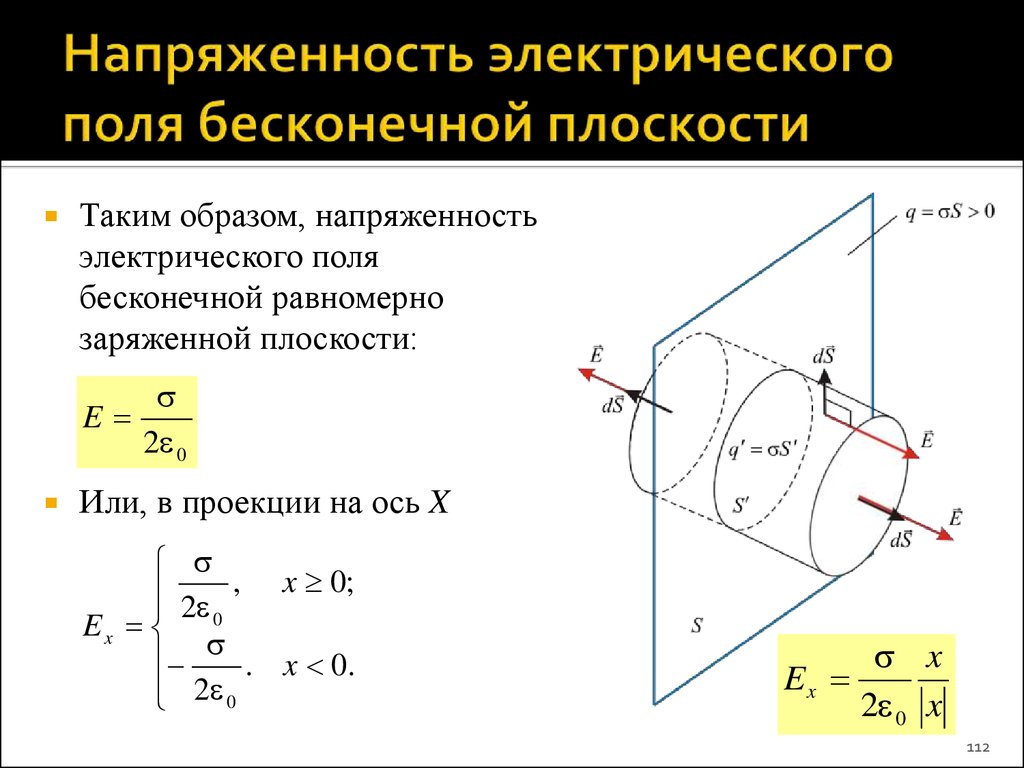
111. Постановка задачи
За гауссову поверхность удобнопринять поверхность цилиндра,
образующие которого
перпендикулярны плоскости, а
основания площадью S
параллельны ей и лежат по
разные стороны от нее на
одинаковых расстояниях.
как векторы E направлены вдоль
оси X: E = Exi и Ex(x) = –Ex(–x),
то
q S
S EdS 2ES 0 0
111
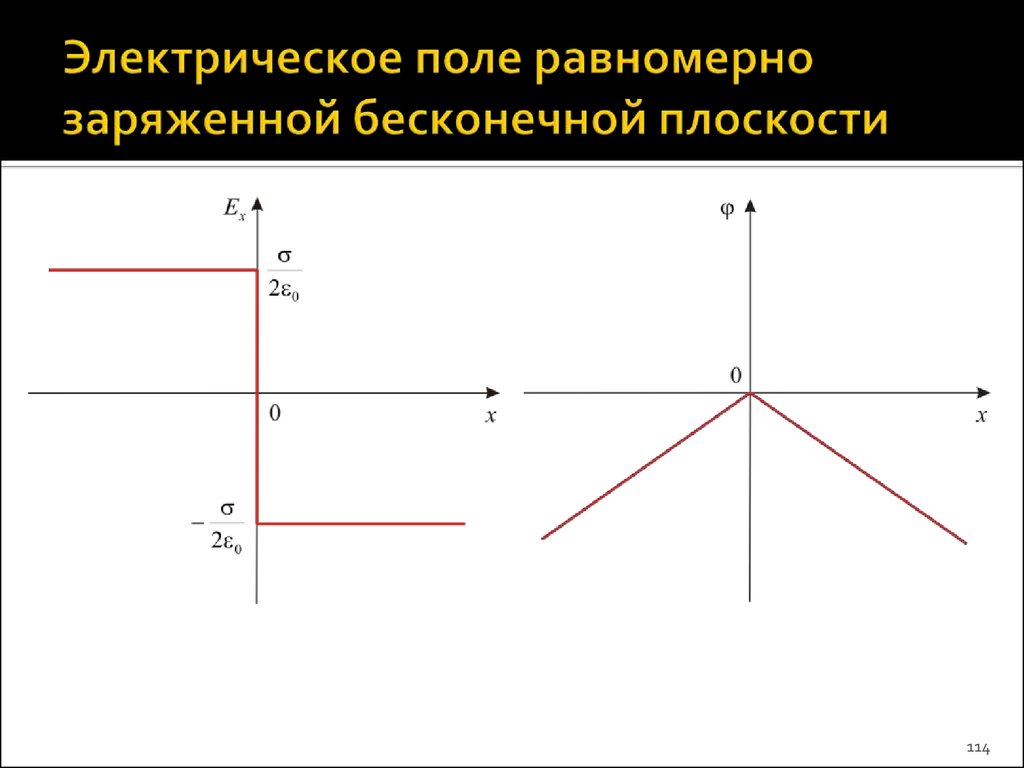
112. Напряженность электрического поля бесконечной плоскости
Таким образом, напряженностьэлектрического поля
бесконечной равномерно
заряженной плоскости:
E
2 0
Или, в проекции на ось X
2 , x 0;
Ex 0
. x 0.
2 0
x
Ex
2 0 x
112
113. Потенциал электрического поля бесконечной плоскости
Так как Ex = –d /dx, то полагая потенциал = 0 во всехточках заряженной плоскости, т.е. (x = 0) = 0, получаем:
при x > 0:
d
,
x
dx
2 0
2 0
при x < 0:
d
,
x
dx 2 0
2 0
Или
x
2 0
113
114. Электрическое поле равномерно заряженной бесконечной плоскости
114115. 1.6 Применение теоремы Гаусса для расчета электрических полей
1.6.5 ЭЛЕКТРИЧЕСКОЕ ПОЛЕ ДВУЗ ПАРАЛЛЕЛЬНЫХ РАВНОМЕРНОЗАРЯЖЕННЫХ БЕСКОНЕЧНЫХ ПЛОСКОСТЕЙ
115
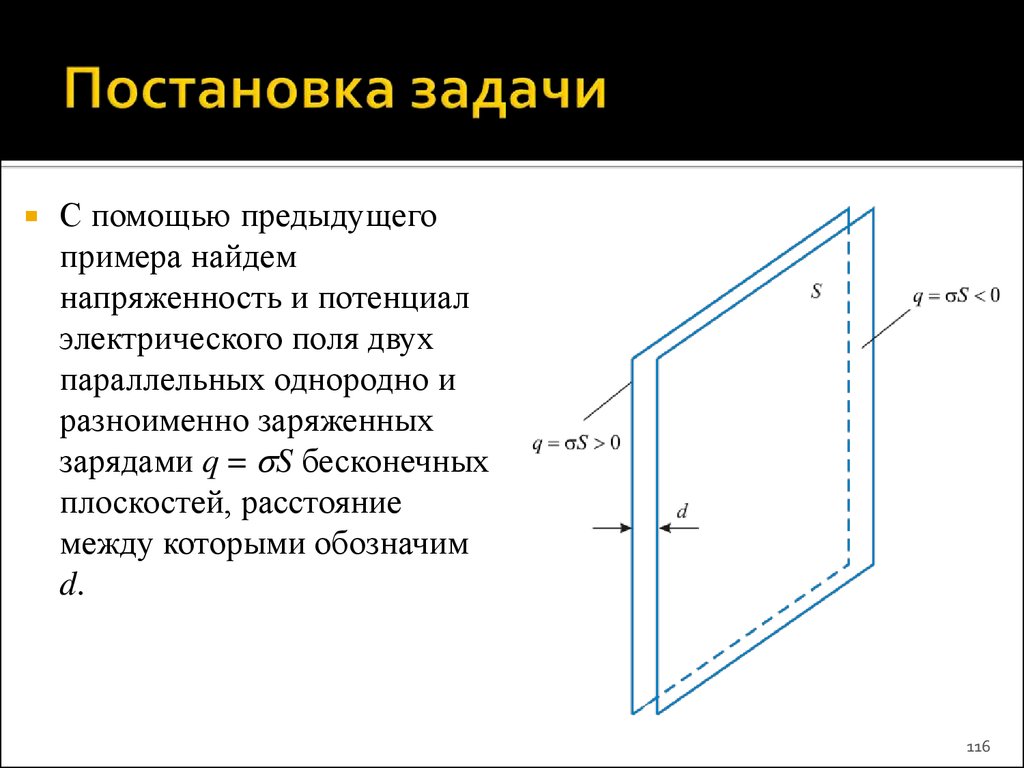
116. Постановка задачи
С помощью предыдущегопримера найдем
напряженность и потенциал
электрического поля двух
параллельных однородно и
разноименно заряженных
зарядами q = S бесконечных
плоскостей, расстояние
между которыми обозначим
d.
116
117. Напряженность электрического поля двух равномерно разноименно заряженных бесконечных плоскостей
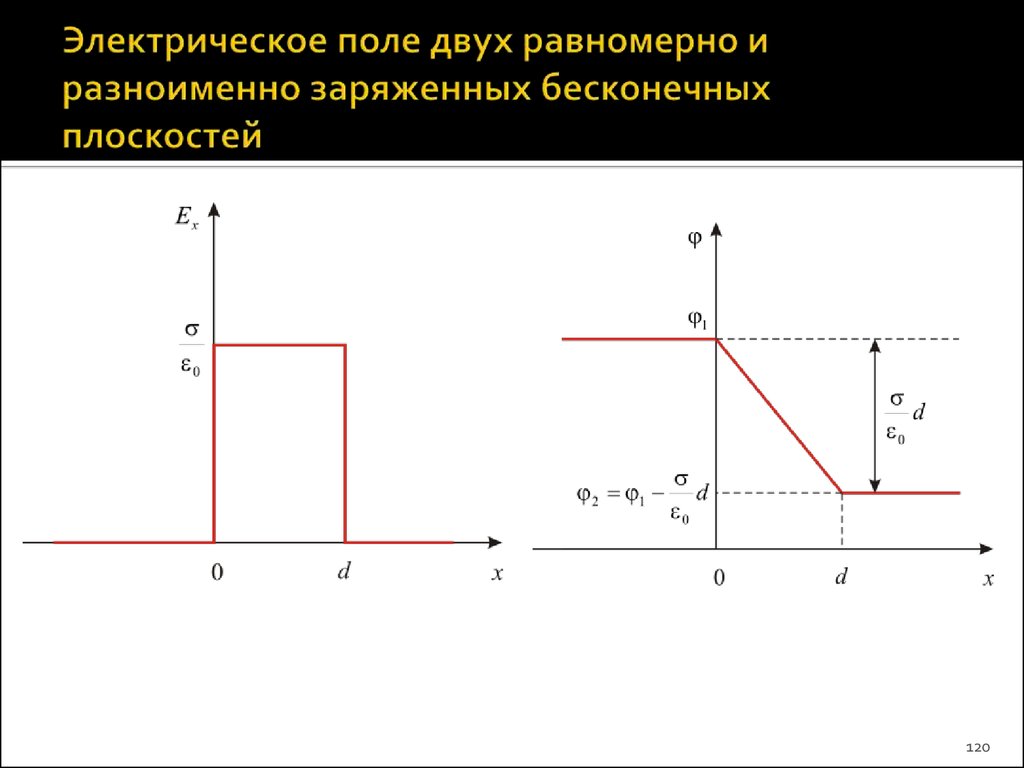
Из предыдущего примераследует, что модули векторов
E1 и E2 напряженностей полей
первой и второй плоскостей
равны по модулю:
E1 E 2
2 0
и всюду направлены
параллельно оси X,
перпендикулярной плоскостям.
117
118. Напряженность электрического поля двух равномерно разноименно заряженных бесконечных плоскостей
Согласно принципусуперпозиции полей,
E1 E 2 E
тогда, слева от первой
плоскости (x < 0) и справа от
второй плоскости (x > d) поле
отсутствует: E = 0
В области между плоскостями:
E 2E1
E
0
118
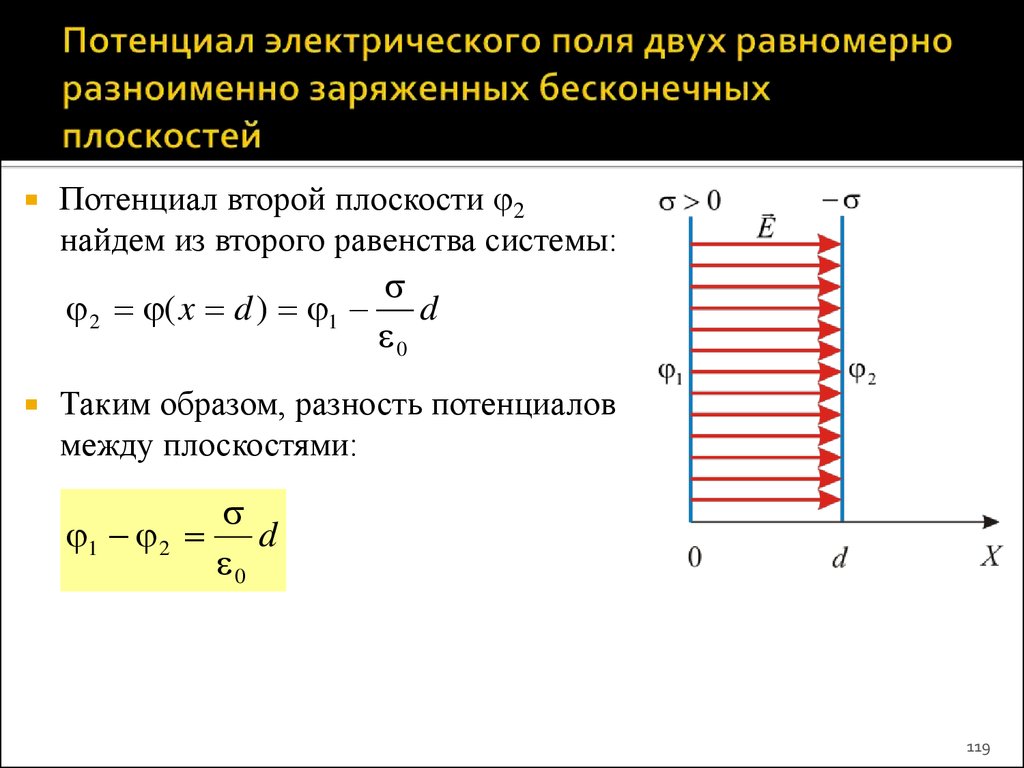
119. Потенциал электрического поля двух равномерно разноименно заряженных бесконечных плоскостей
Потенциал второй плоскости 2найдем из второго равенства системы:
2 ( x d ) 1 d
0
Таким образом, разность потенциалов
между плоскостями:
1 2 d
0
119






















































































 Физика
Физика








