Основы теории картографических проекций. Масштаб (лекция № 9)

1.

Федеральное государственное бюджетное образовательное учреждение высшего образования
Калининградский государственный технический университет
«Балтийская государственная академия рыбопромыслового флота»
(БГАРФ ФГБОУ ВО КГТУ)
Раздел 4. Картографические проекции и морские
навигационные карты.
Лекция № 9 (4.1)
Тема:
Калининград
2021
Доцент кафедры судовождения,
кандидат военных наук, доцент Щавелев В.П.
1

2.

Цель лекции. Учебные вопросы
Цель лекции:
- формирование конвенционных компетентностей в части,
касающейся картографических проекций при ведении счисления с
учетом ветра, приливов, течений и рассчитанной скорости.
Учебные вопросы лекции:
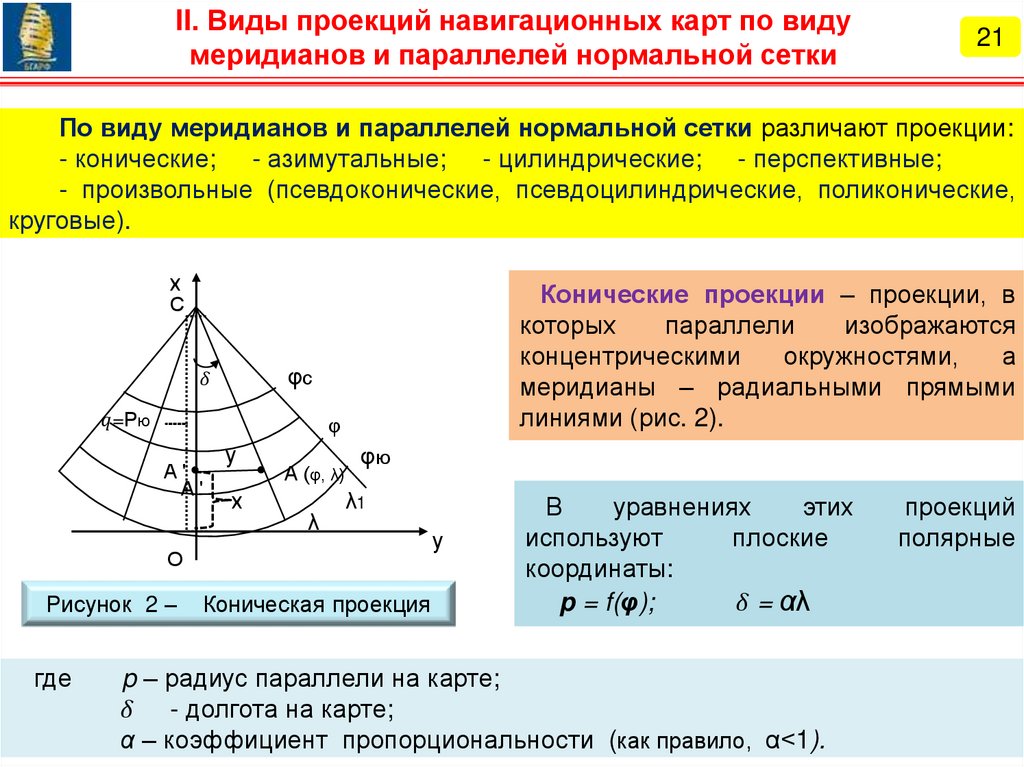
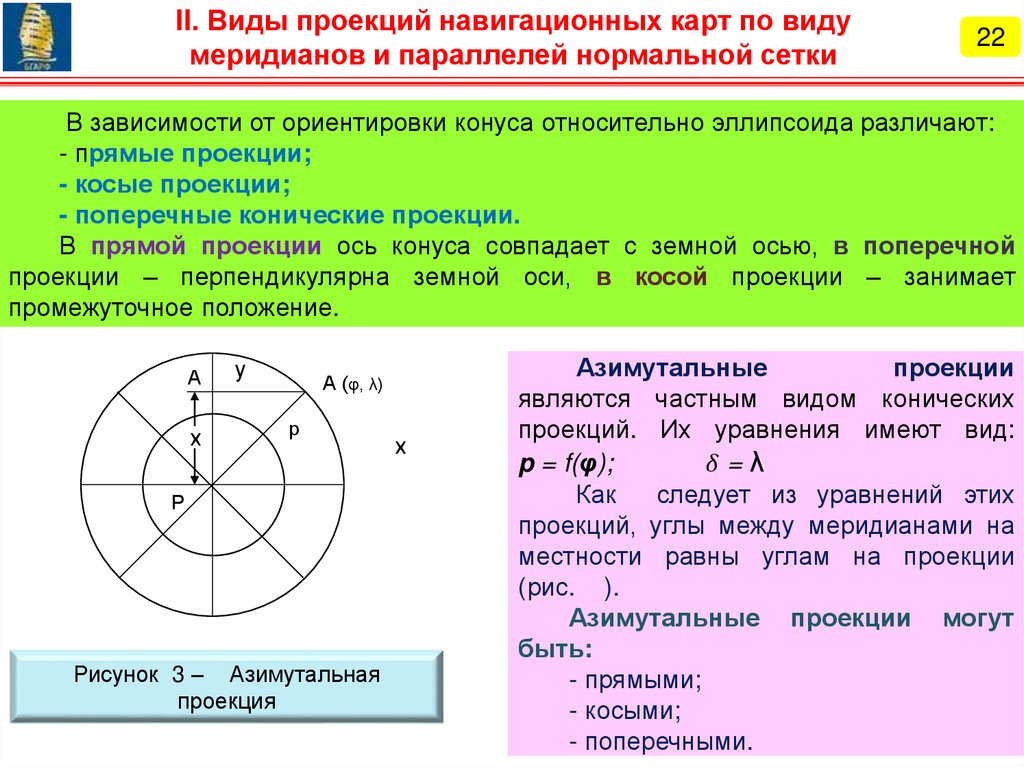
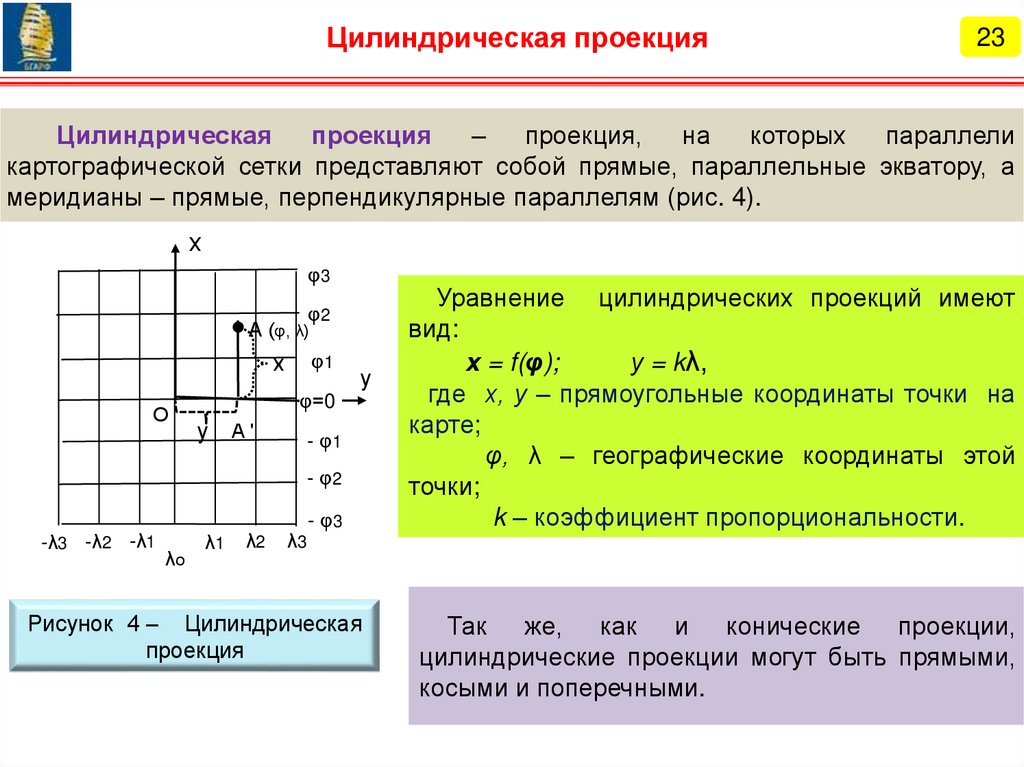
1. Основы теории картографических проекций.
2.
Масштаб.
Предельная
точность
масштаба.
Характеристика искажений проекции.
3. Классификация картографических проекций.
2

3.

Литература
3
Основная:
1. Дмитриев В.И, Рассукованый Л. С. Навигация и лоция, навигационная
гидрометеорология, электронная картография (+CD). Учебник. – Москва:
Моркнига, 2018 . – 312 с. - ISBN: 978-5-030033-52-5.
2. Дмитриев В.И., Григорян В.Л., Катенин В.А. Навигация и лоция. Учебник
для вузов (3-е издание переработанное и дополненное)/Под общ. Ред. д.ф.т.н.,
проф. В.И. Дектярева. – М.: «МОРКНИГА», 2009. – 458 с.: ил.

4.

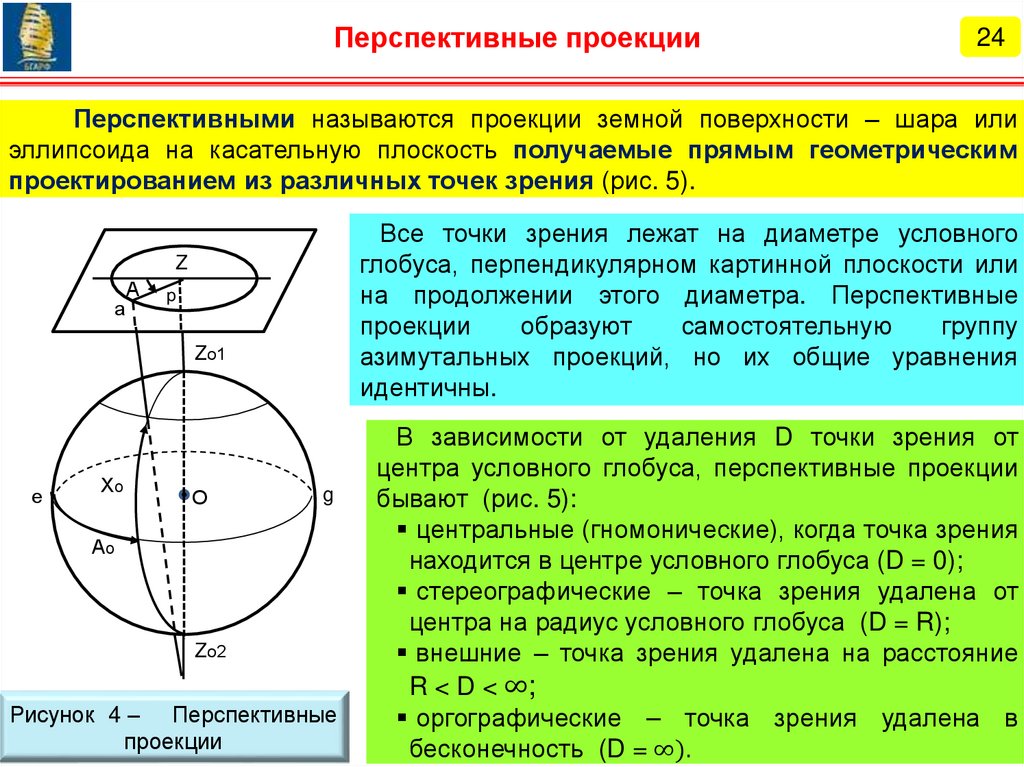
Первый учебный вопрос
1. Основы теории картографических проекций.
4

5.

Картография
5
Картография – область науки, техники и производства, изучающая
создание и использование картографических произведений.
Картография подразделяется на:
- математическую картографию;
- картометрию;
- проектирование и составление карт;
- оформление;
- составление карт.
Математическая
картография
разрабатывает
вопросы
математического обоснования карт и является первой ступенью в
процессе создания карт.
Картографируемая поверхность Земли имеет сложную конфигурацию
и неправильную геометрическую форму, а поэтому не может быть описана
математическими формулами. Для отображения ее на плоскости
необходимо от физической поверхности Земли перейти к ее
математической модели. Такая математическая модель будет весьма
близка к физической поверхности. Однако уже выражена математическими
формулами.

6.

Картография
6
При картографировании
за модель Земли принимают шар или
эллипсоид вращения, малая ось которого совпадает с осью вращения
Земли. Эти фигуры нельзя развернуть на плоскости без искажений,
поэтому
при
создании
карт
используют
различные
способы
проектирования, отличающиеся свойствами этих искажений.
Основная задача математической картографии – проектирование
на плоскость системы географических координат (сетки параллелей и
меридианов), пользуясь которой затем на карту наносятся элементы ее
нагрузки.
Картографическая проекция – математически выраженный закон,
связывающий географические координаты некоторой точки на
поверхности криволинейной модели Земли с прямоугольными
координатами этой же точки на плоскости.
Общее уравнение картографических проекций:
х = f1 (φ, λ);
у = f2 (φ, λ).
где: φ и λ – криволинейные географические координаты некоторой точки на
картографируемой поверхности;
х и у - прямоугольные координаты изображения этой же точки на
плоскости в проекции, определяемой функциями f1 и f2.

7.

Картография
7
Свойства проекции будут зависеть от свойств и характера функций f1 и
f2. Поскольку этих функций может быть множество, то и получаемые
проекции тоже могут быть разнообразными.
Картографическая сетка – изображение
меридианов параллелей на плоскости.
семейства
линий
Каждой проекции соответствует определенная картографическая
сетка, которая и составляет математическую основу создаваемых карт.
Параллель - линия, соединяющая точки одинаковых значений
широты.
Меридиан - линия, соединяющая точки равных значений долготы.
Географическая сетка - сеть параллелей и меридианов (как правило,
регулярная) на эллипсоиде или шаре.

8.

Второй учебный вопрос
2. Масштаб. Предельная точность масштаба.
Характеристика искажений проекции.
8

9.

Масштаб карты
9
Карта должна быть не только плоским, но и уменьшенным изображением
плоскости. Поэтому, прежде чем проектировать на плоскость, картографируемую
поверхность уменьшают до необходимых размеров.
Полученная математическая модель Земли в заданном масштабе, называется
условный глобус.
Каждая карта имеет главный масштаб, который показывает общую степень
уменьшения всей картографируемой поверхности при изображении на плоскости
(карте):
µ0 = ds0 /dS0
где: µ0 - главный масштаб карты;
ds0 - бесконечно малый отрезок на поверхности условного глобуса;
dS0 соответствующий
ему
бесконечно
малый
отрезок
на
картографируемой поверхности.
После проектирования – разворачивания поверхности условного
глобуса на плоскость – главный масштаб сохраняет свое численное
значение лишь в определенных точках или вдоль некоторых линий на
карте. Точка карты (линия), в которой масштаб изображения равен
главному масштабу, называется центральной точкой (центральной
линией) проекции.

10.

Масштаб карты
10
Во всех остальных точках карты масштаб изображения будет отличаться от
главного. Поэтому кроме главного масштаба µ0 различают еще и частный
масштаб:
µ = ds /dS0 ,
где: µ - частный масштаб карты;
ds – бесконечно малый отрезок на карте;
dS0 – соответствующий ему
бесконечно малый отрезок на
картографируемой поверхности.
Таким образом:
- главный масштаб характеризует общее уменьшение изображения;
- частный масштаб характеризует степень уменьшения изображения только в
данной точке карты.
Увеличение масштаба - отношение частного масштаба в данной точке к
главному масштабу, характеризует степень искажения проекции: расхождение
фактического масштаба карты с масштабом условного глобуса:
С = µ/µ0 = ds/ ds0
Увеличение масштаба изменяется при переходе от одной точки карты к
другой, а также по разным направлениям, проложенным из одной и той же точки.
Это приводит к искажению длин, направлений, углов и площадей на проекции.

11.

Масштаб карты
11
Чем ближе увеличение масштаба к единице во всех точках карты, тем
лучше и совершеннее выбранная для данной карты проекция.
Относительное искажение длин или просто искажением длин разность между увеличением масштаба С и единицей:
V = C – 1 = µ/µ0 - 1 = (µ - µ0 )/µ0
Если известны главный масштаб карты и ее частный масштаб в данной
точке, то искажение длин может быть подсчитано.
Например: исходные данные:
главный масштаб µ0 = 1: 500000;
частный масштаб µ = 1: 434780.
Решение:
увеличение масштаба – С = 1,15; искажение длин V - 0,15, = + 15%.
Пусть на карте отрезок равен 50 мм, что при главном масштабе 1:
500000 соответствует расстояние 25000 м.
Следовательно,
действительное
расстояние
на
местности,
соответствующее данному отрезку карты, будет равно 25000 : 1,15 =
21739 м.

12.

Масштаб карты
12
На картах показывают только главный масштаб, который может быть
выражен в двух видах – числовом и линейном.
Числовой масштаб изображается в виде дроби, числитель которой
единица, знаменатель показывает, какова степень уменьшения длин на
условном глобусе.
Например: М = 1/10000 или М = 1/750000.
Возможна и такая форма записи масштаба:
М = 1:100000 или М = 0, 000001.
При графической работе на карте чаще используют линейный
масштаб, показывающий число единиц, принятых для измерения длин на
местности (км, мили), которое содержится в единице, принятой для
измерения длин на карте (мм, см).
Линейный масштаб на специально вычерченной шкале показывает
число километров, содержащихся в одном миллиметре или число миль, в
одном сантиметре.
Иногда вместо построения шкалы ограничиваются указанием:
- в 1 см – 1 кбт;
- в 1 см – 2 мили.

13.

Масштаб карты
13
Линейный масштаб:
на морских навигационных картах в проекции Меркатора строят
вдоль боковых рамок карты;
на топографических и географических картах вычерчивают под
нижней рамкой карты в виде короткой шкалы.
С уменьшением масштаба карты изображения небольших объектов
становятся настолько малыми, что нанесение их на карту становится
невозможным. Практикой установлено, что разрешающая способность
невооруженного глаза человека равна 0,1 мм. Поэтому две точки,
находящиеся на расстоянии менее 0,1 мм одна от другой, усматриваются
как одна. В соответствии с этим свойством зрения человека принято
линейное расстояние на местности, соответствующее на карте отрезку в
0,1 мм, называть предельной точностью масштаба (ПТМ). Кроме того,
при составлении карты неизбежны некоторые неточности за счет
погрешностей проектирования, вычерчивания контуров и погрешностей за
деформацию бумаги. Поэтому при работе на карте условились считать, что
предельная точность масштаба – это расстояние на местности,
соответствующее отрезку на карте, равному 0,2 мм.

14.

Предельная точность масштаба
14
Предельная точность масштаба:
- зависит от масштаба карты;
- выражается в метрах;
- рассчитывается по формуле:
ПТМ = 0,0002 С (м)
где С – знаменатель главного масштаба карты.
Пример: для карты масштаба 1 : 500 000 ПТМ = 0,0002 × 500 000 =
100 м.
По сути, предельная точность масштаба равна тому минимальному
расстоянию на местности, которое может быть изображено на карте.
Масштаб и предельная точность масштаба карты характеризуют
разрешающую способность данной карты, тем самым определяя
допустимую погрешность, с которой на этой карте могут выполняться
графические построения.

15.

Характеристика искажений проекции
15
Величины искажений являются одним из основных критериев оценки
достоинства карты. При картографировании искажения неизбежны, однако они
подчиняются некоторым закономерностям и поэтому поддаются учету при работе
на карте. Полную и наглядную характеристику искажений любой проекции в любой
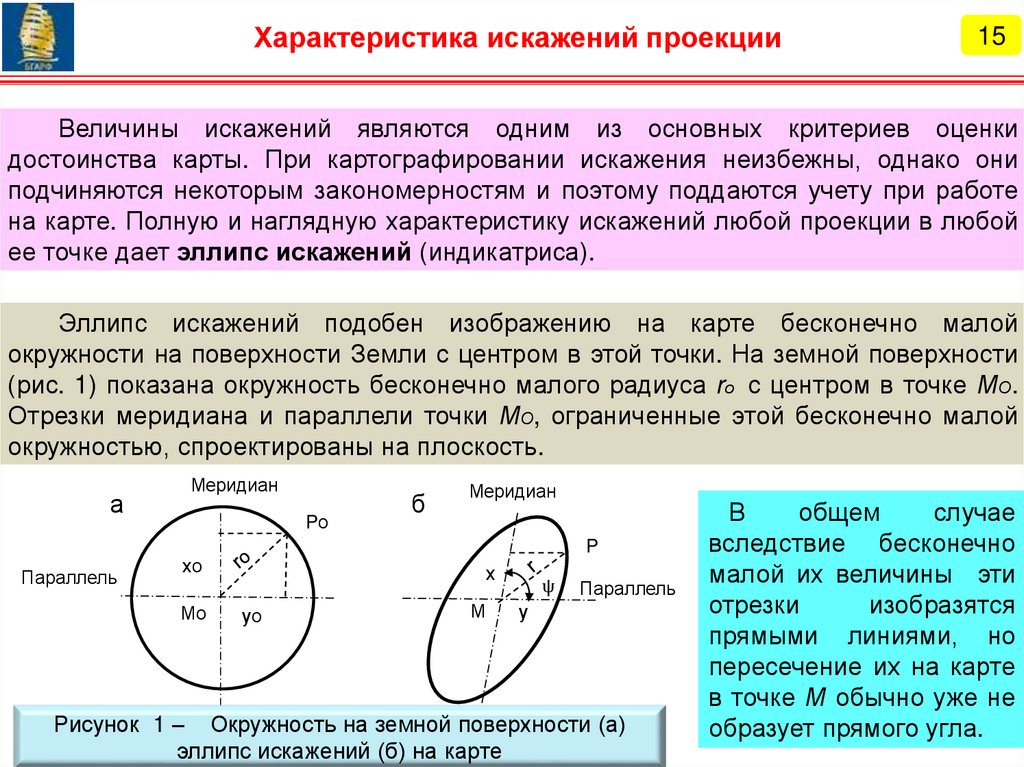
ее точке дает эллипс искажений (индикатриса).
Эллипс искажений подобен изображению на карте бесконечно малой
окружности на поверхности Земли с центром в этой точки. На земной поверхности
(рис. 1) показана окружность бесконечно малого радиуса rо с центром в точке МО.
Отрезки меридиана и параллели точки МО, ограниченные этой бесконечно малой
окружностью, спроектированы на плоскость.
а
Параллель
Меридиан
Pо
Меридиан
P
хо
Мо
б
х
уо
М
ѱ
Параллель
у
Рисунок 1 – Окружность на земной поверхности (а)
эллипс искажений (б) на карте
В
общем
случае
вследствие бесконечно
малой их величины эти
отрезки
изобразятся
прямыми линиями, но
пересечение их на карте
в точке М обычно уже не
образует прямого угла.

16.

Характеристика искажений проекции
16
Если на земной поверхности точка окружности РО имеет прямоугольные
координаты хо и уо, то проекция этой точки Р на плоскости проекции (карты) имеет
косоугольные координаты х и у.
Обозначив масштаб вдоль меридиана m, а вдоль параллели n, согласно
определению масштаба: