Поток энергии. Поток импульса. Сила сопротивления при потенциальном обтекании

1. Лекция 3 «Гидродинамика идеальной жидкость»

Содержание
1.
2.
3.
Поток энергии.
Поток импульса.
Сила сопротивления при потенциальном обтекании.

2.

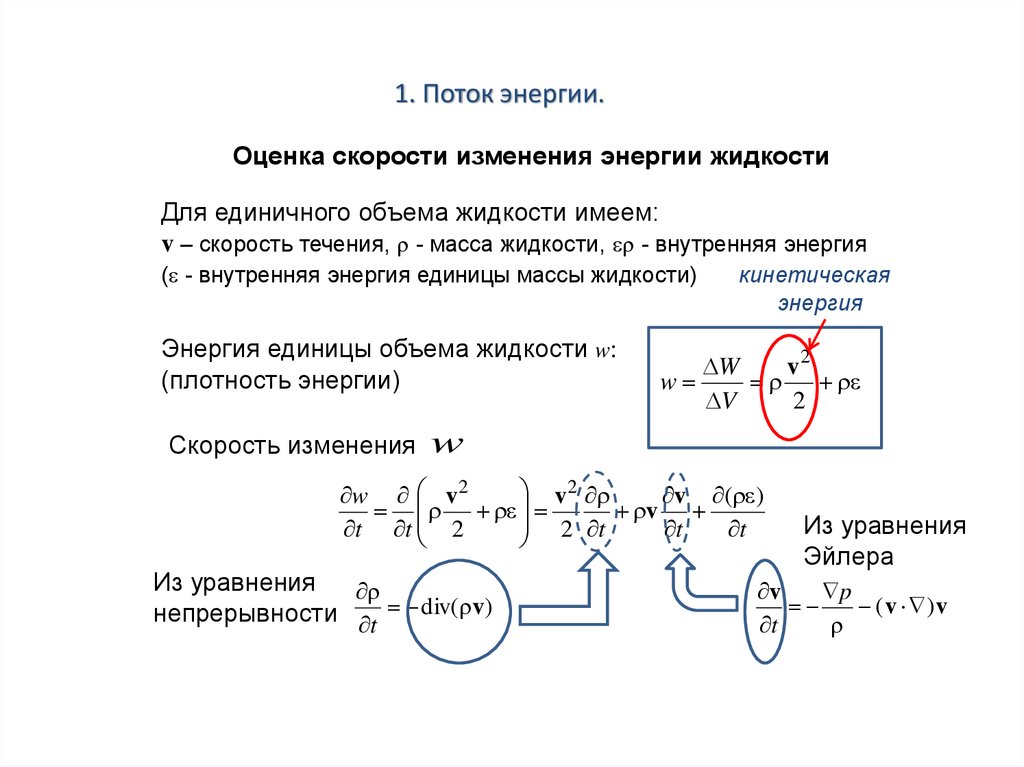
1. Поток энергии.
Оценка скорости изменения энергии жидкости
Для единичного объема жидкости имеем:
v – скорость течения, - масса жидкости, - внутренняя энергия
( - внутренняя энергия единицы массы жидкости)
Энергия единицы объема жидкости w:
(плотность энергии)
Cкорость изменения
кинетическая
энергия
W
v2
w
V
2
w
v 2
w v 2
v ( )
v
2 t
t t 2
t
t
Из уравнения
непрерывности t div( v)
Из уравнения
Эйлера
v
p
( v ) v
t

3.

w
v2
( )
div( v) v p v( v ) v
t
2
t
Из термодинамического
определения энтальпии
dh Tds dp /
v( v ) v v ( v 2 )
2
p h T s
w
v2
( )
div( v) v h v ( v 2 )
v T s
t
2
2
t
2
v
v h
2
2
w
v2
v
( )
div( v) v h
v T s
t
2
2
t
Из I начала
термодинамики
d Tds pdV
и т.к. соотнесена к единице
массы, то здесь V 1/ и
dV d / 2

4.

W
v2
w
V
2
p
d ( ) d d d Tds
p
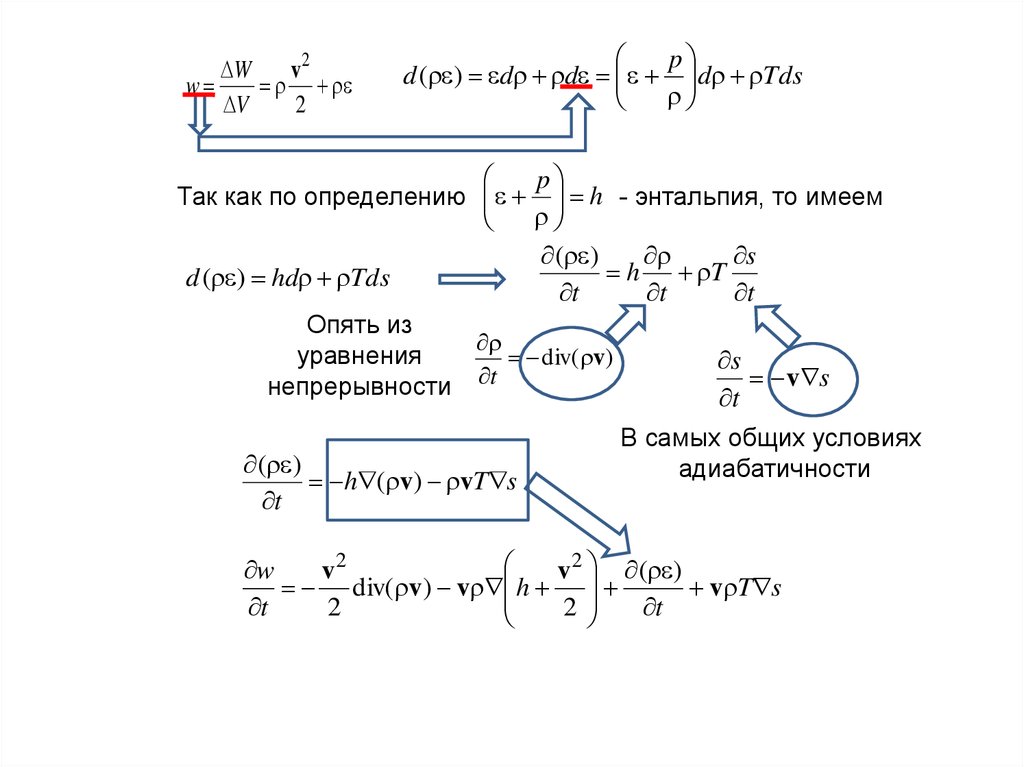
Так как по определению h - энтальпия, то имеем
( )
s
h
T
d ( ) hd Tds
t
t
t
Опять из
уравнения
div( v)
s
t
v s
непрерывности
t
( )
h ( v) vT s
t
В самых общих условиях
адиабатичности
2
w
v2
v
( )
div( v) v h
v T s
t
2
2
t

5.

2
w
v2
v
( v) v h h ( v) Tv s v T s
t
2
2
2
2
2
w
v2
v
v
v
( v) v h h ( v) h ( v) ( v ) h
t
2
2
2
2
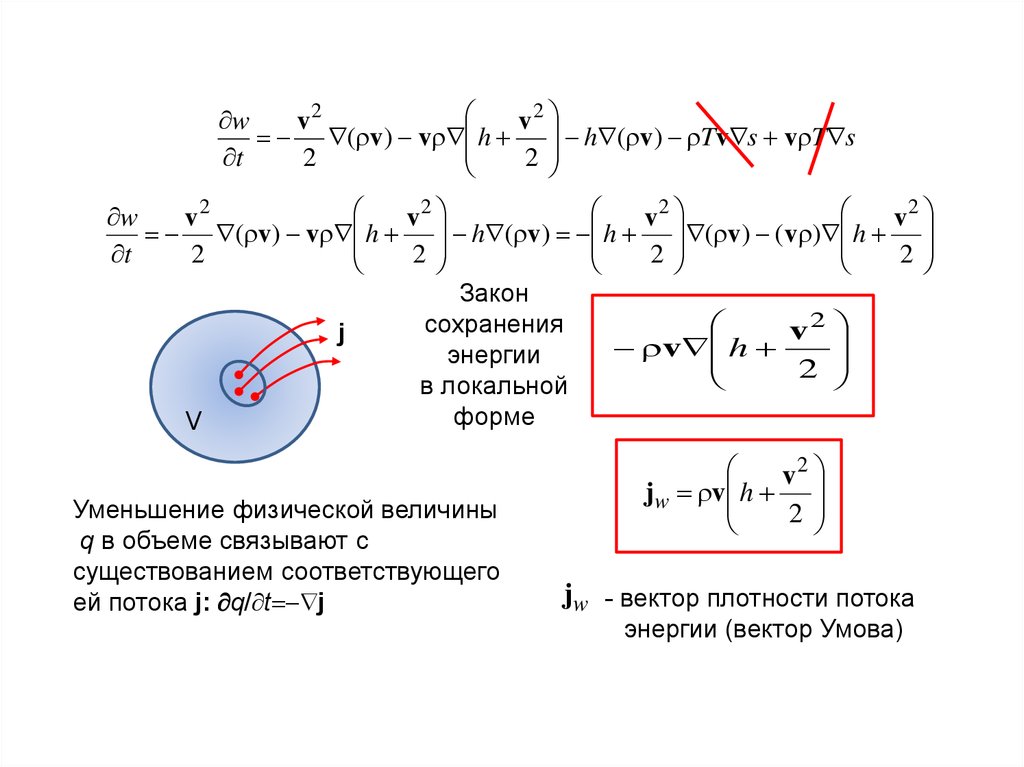
Закон
2
сохранения
v
j
v h
энергии
2
в локальной
форме
V
Уменьшение физической величины
q в объеме связывают с
существованием соответствующего
ей потока j: q/ t j
2
v
jw v h
2
jw - вектор плотности потока
энергии (вектор Умова)

6.

p
Учитывая, что h имеем
v 2
jw v
2
p vw pv
Плотность потока энергии определяется из собственно
переноса энергии текущей жидкостью vw и дополнительного
вклада в поток, вносимого работой сил давления p над
жидкостью pv
w
В случае стационарных течений
0
Из закона сохранения энергии имеем t
w
0 jw 0 т.е.
t
[ v( p v2 / 2)] ( p v2 / 2) v v ( p v2 / 2) 0
v 0
p v2 / 2 const
Для несжимаемой жидкости имеем дополнительно
и т.к. v 0
При gh
( p v2 / 2) 0
(однородное поле тяготения) получаем закон Бернулли
в его классическом виде
2
p gh v / 2 const

7.

2. Поток импульса.
Импульс единицы объема v или в тензорных обозначениях vi
v
Скорость изменения импульса
( vi ) i vi
t
t t
Уравнение непрерывности ( v k )
t
xk
v
p
( vk )
( vi ) vk i
vi
t
xk xi
xk
Сумма этих членов равна
( vi v k )
xk
vi
v 1 p
vk i
t
xk xi
Уравнение Эйлера
p
p
ik
xi
xk
p
( vi )
( vi vk ) ik
( vi vk p ik )
t
xk
xk
xk

8.

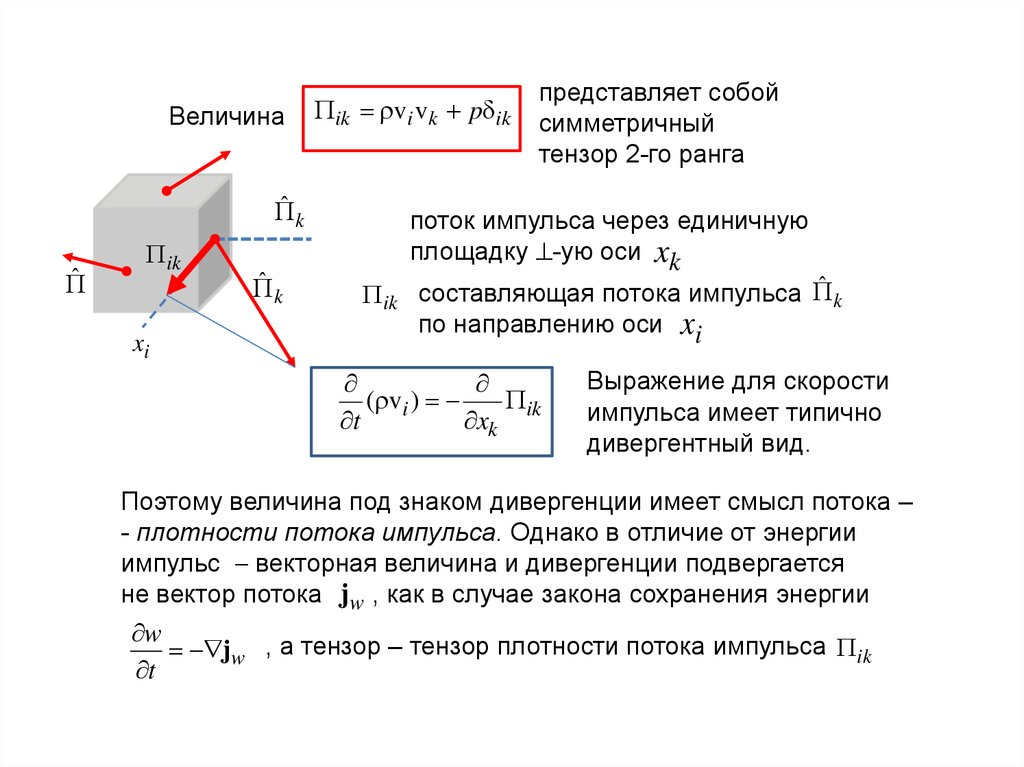
Величина
ˆk
ˆ
ik
xi
ˆk
ik vi v k p ik
представляет собой
симметричный
тензор 2-го ранга
поток импульса через единичную
площадку -ую оси xk
ˆk
ik составляющая потока импульса
по направлению оси xi
( vi )
ik
t
xk
Выражение для скорости
импульса имеет типично
дивергентный вид.
Поэтому величина под знаком дивергенции имеет смысл потока –
- плотности потока импульса. Однако в отличие от энергии
импульс векторная величина и дивергенции подвергается
не вектор потока jw , как в случае закона сохранения энергии
w
jw , а тензор – тензор плотности потока импульса ik
t

9.

В произвольном направлении, задаваемом единичным вектором
n, величина тензора ik будет определяться сверткой ik nk
ik nk p ik nk vi v k nk pni vi v k nk
Данная величина является вектором и может быть записана
в явном виде
Π pn v( v n)
p
0
v
Характеристическая поверхность тензора ik получается
сверткой ik nk ni Π n p v2 cos2 и является эллипсоидом
вращения вокруг направления вектора скорости.

10.

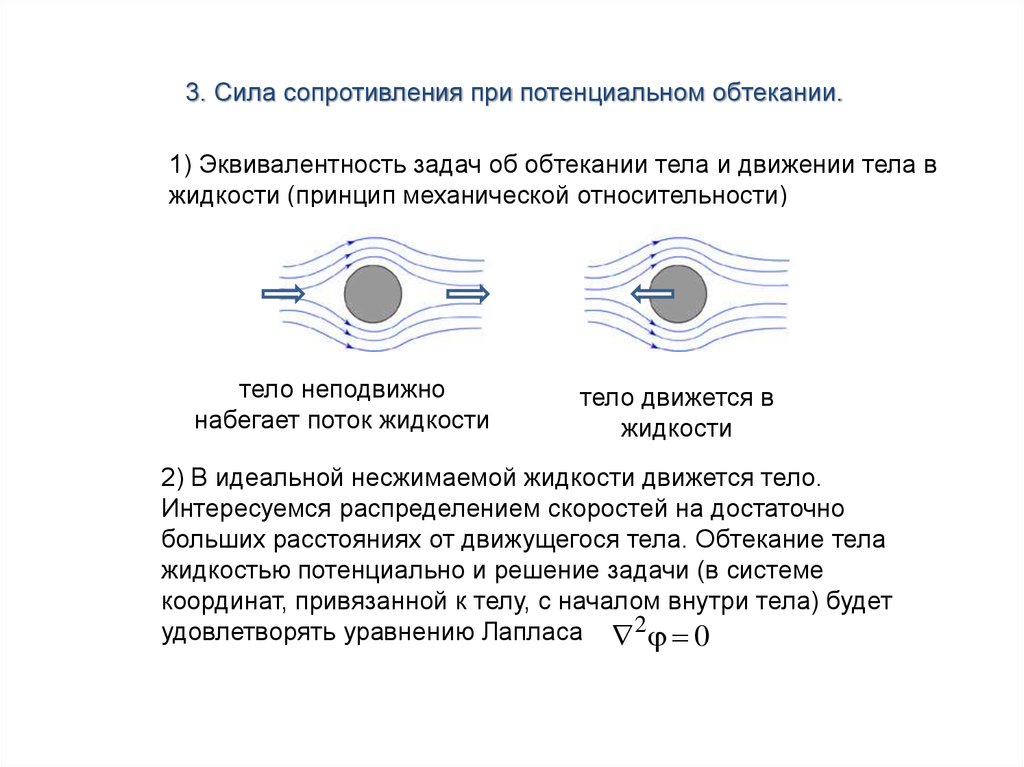
3. Сила сопротивления при потенциальном обтекании.
1) Эквивалентность задач об обтекании тела и движении тела в
жидкости (принцип механической относительности)
тело неподвижно
набегает поток жидкости
тело движется в
жидкости
2) В идеальной несжимаемой жидкости движется тело.
Интересуемся распределением скоростей на достаточно
больших расстояниях от движущегося тела. Обтекание тела
жидкостью потенциально и решение задачи (в системе
координат, привязанной к телу, с началом внутри тела) будет
удовлетворять уравнению Лапласа 2 0

11.

3) Общие замечания относительно решения
• на большом (бесконечном) удалении от тела жидкость
покоится и (r ) 0
• математически задача аналогична электростатической
задаче для внешней области и потенциал представляется
мультипольным разложением вида
a
2 1
1
A bik
r
xi xk r
r
• a должно быть 0 иначе существует радиальный поток
через замкнутую поверхность, охватывающую тело, что
противоречит условию несжимаемости жидкости
• на больших расстояниях r достаточно ограничиться дипольным
приближением
A n
1
A 2
r
r
Здесь n - единичный вектор в направлении радиус-вектора.

12.

4) Оценка кинетической энергии W жидкости, индуцированной
движением тела
1 3( A n)n A
v ( A )
По определению v= имеем
r
r3
(A - аналог дипольного момента, v - аналог напряженности)
W
2
2
v
dV
u
dV
( v u)( v u)dV
2V
2V
2V
u скорость движения тела, V объем жидкости
После преобразований имеем
W (4 A u V0u 2 )
2
Вектор A определяется размерами и формой тела.
Для этого нужно построить решение граничной задачи.
Однако общий характер связи A с u можно установить,
не прибегая к решению граничной задачи.

13.

5) Тензор присоединенных масс и полный импульс жидкости.
Вследствие линейности связи A и , и линейности граничных
условий W u2 и в общем случае можно принять
W
mik uiuk
2
mik - тензор присоединенных масс
При бесконечно малых изменениях энергия W и импульс
жидкости P связаны между собой равенством
dW udP
Отсюда вытекает, что
Pi mik uk
Передаваемый за ед. времени от тела жидкости импульс по
3 закону Ньютона равен с изменением знака силе реакции
со стороны жидкости на тело, т.е.
Fi
dPi
d
(mik uk )
dt
dt

14.

6) Выводы
• если тело в процессе движения не меняет свою форму и
ориентацию, то mik const и сила реакции отсутствует,
если движение тела равномерное (парадокс Даламбера)
• определение импульса через посредство коэффициентов
присоединенных масс приводит к уравнению движения тела
в жидкости под действием внешней силы f вида
duk
( M ik mik ) fi
dt
Видно, что тело в жидкости, как бы увеличивает свою массу
M на величину mik , что и явилось поводом для введения
термина «присоединенная масса».