Похожие презентации:
Проводники в электрическом поле (лекция 3)
1. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
Носители заряда в проводнике (электроны) перемещаются под действиемсколь угодно малой силы. Если сообщить проводнику заряд , то он практически мгновенно распределится по нему и займет равновесное положение. При этом внутри проводника напряженность электрического поля
будет равна нулю, т.к. в противном случае заряды внутри начнут перемещаться и равновесие нарушится. По этой же причине весь заряд будет
находиться на поверхности проводника. Заряды внутри проводника привели бы по теореме Гаусса к появлению отличного от нуля потока вектора
напряженности и возникновению не равной нулю напряженности поля
внутри проводника. Если напряженность E на поверхности составляет с
ней некоторый угол (рис. 14), то составляющая вдоль поверхности E
приведет к движению зарядов вдоль поверхности и нарушит их уже установившееся равновесие. Таким образом, равновесие зарядов на проводнике возможно при выполнении двух условий: внутри проводника E =0, а на
поверхности E En , и сама поверхность является эквипотенцииальной.
На этом основана защита проводников от внешних электрических полей.
На рис. 15 изображены линии напряженности электрического поля, в котором находится проводник, пунктиром показаны линии напряженнос-ти в
2. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
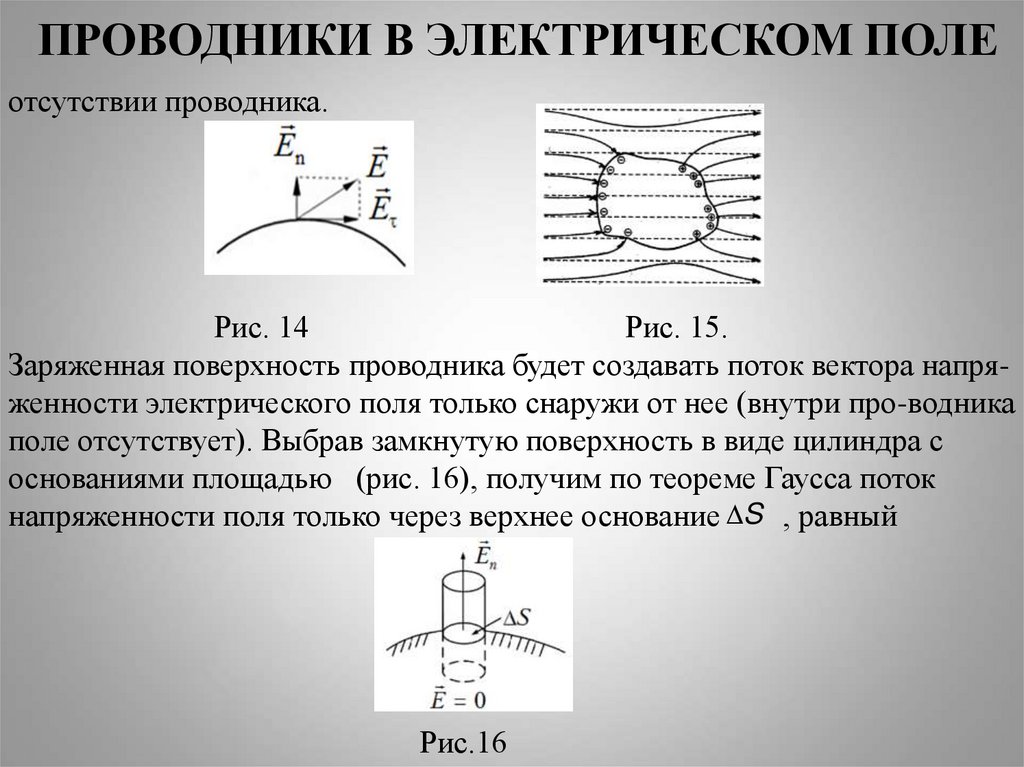
отсутствии проводника.Рис. 14
Рис. 15.
Заряженная поверхность проводника будет создавать поток вектора напряженности электрического поля только снаружи от нее (внутри про-водника
поле отсутствует). Выбрав замкнутую поверхность в виде цилиндра с
основаниями площадью (рис. 16), получим по теореме Гаусса поток
напряженности поля только через верхнее основание S , равный
Рис.16
3. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
s S Тогда E s , где s - поверхностная плотность зарядаn
En S
.
e0e
e0
проводника, e - диэлектрическая проницаемость среды, окружающей
проводник.
Электроемкость
Распределение заряда на уединенном проводнике не зависит от величины
заряда. Плотность заряда влияет на электрическое поле на поверхности
проводника и, следовательно, на потенциал его поверхности. Таким
образом, заряд уединенного проводника пропорционален его потенциалу
q
- емкость проводника. Емкость численно равна
q C , где C
заряду, который надо сообщить проводнику, чтобы его потенциал
увеличился на 1 В. При 0 величина емкости стремится к бесконечности.
q
Потенциалзаряженной сферы радиусом R равен
, откуда
4 e0eR
емкость сферы C 4 e0eR . Единицей емкости является фарада (1 Ф) емкость такого проводника, при сообщении которому заряда в 1 Кл, его
4. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
потенциал изменяется на 1 В.Конденсаторы
Конденсатором называется система из двух проводников, называемых
обкладками, несущих заряды, равные по величине, но противоположные
по знаку. Емкость конденсатора зависит от расположения проводников.
Идеальный плоский заряженный конденсатор (рис. 17) создает электрическое поле только между пластинами. Конденсаторы используются в
выпрямителях переменного тока, в цепочках дифференцирования и интегрирования, различных микросхемах.
Рис.17
Емкость любого конденсатора определяется соотношением
C
q
.
1 2
5. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
Разность потенциалов на обкладках конденсатора равна1 2 Ed
sd
qd
q
,
e0e e0eS C
откуда емкость плоского конденсатора равна C e0eS . Очевидно, что .
d
C Ф
.
e0
d м
Заряд, напряжение и емкость конденсатора связаны соотношением q CU .
Цилиндрический конденсатор
Напряженность электрического поля единицы длины заряженной нити и
цилиндра равны E 1 q , а разность потенциалов между двумя
2 e0e r
R2
q dr
q
2 e0e r
2 e0e
R1
цилиндрическими пластинами (рис. 18) 1 2
.
Рис. 18
n
R2
,
R1
6. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
тогда емкость конденсатора равна2 e0e
C
.
n R2 R1
Сферический конденсатор
Напряженность электрического поля сферы равна E
q
,
2 а разность
4 e0er
потенциалов между двумя сферами (рис. 19) равна
qdr
qdr 1
1
1 2
,
2
4 e0er
4 e0e R1 R2
R
R2
откуда емкость C
4e0eR1R2
.
R2 R1
Рис. 19
7. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
Соединения конденсаторовПараллельное соединение
При таком соединении (рис. 20) на верхних пластинах потенциал 1, на
нижних 2 и заряд суммарного конденсатора равен
q qi Ci ( 1 2 ) Cпар ( 1 2 ) .
i
i
Общая емкость конденсаторов равна
С пар Ci .
i
При параллельном соединении емкости складываются.
Рис.20
При последовательном соединении (рис. 21) заряды на всех пластинах
одинаковые, а напряжения U i q складываются. Напряжение на соеCi
8. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
динении равно 1 2q
1
U i q .
C
i
i Ci
Рис.21
Если представить незаряженное последовательное соединение конденсаторов и зарядить зарядом q, например, левую пластину первого
конденсатора, то на его правой пластине появится заряд –q, на левой
пластине второго конденсатора появится заряд q и т.д.
Таким образом, при последовательном соединении складываются
обратные величины емкостей конденсаторов 1 1 .
C
i
Ci
Если параллельно соединены n одинаковых конденсаторов с емкостью C0,
то 1 n и C C0 .
C
C0
n
9. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
Примеры решения задачЗадача 16. Три одинаковых воздушных конденсатора соединены
последовательно. После полного заполнения двух их них одним и тем же
диэлектриком емкость системы увеличилась в два раза. Найдите диэлектрическую проницаемость этого диэлектрика.
Решение. Начальная суммарная емкость конденсаторов равна
С
Снач . После заполнения двух конденсаторов диэлектриком емкость
3
каждого из них стала e С ,, а величина обратная общей конечной емкости
Стала
eС
1
1
1 1 2 e
Общая
конечная
емкость
стала
С
.
кон
2 e
Скон eС eС С
eС
в 2 раза больше начальной емкости, откуда e 4.
Задача 17. Три конденсатора емкостями С, 2С и 3С соединили
один раз последовательно, другой раз – параллельно. Найдите, во сколько
раз заряд конденсаторов при параллельном соединении больше, чем при
последовательном соединении, если система подключается к одному и
тому же источнику напряжения.
10. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
Решение. При последовательном соединении складываются обратные величины емкостей 1 1 1 1 6 3 2 11 , а общаяС
С 2С 3С
6С
6С
6С посл
емкость равна Спосл . При параллельном соединении общая емкость
11
Спар С 2С 3С 6С.
Заряд системы при подключении к одному и тому же источнику напряжения U равен в обоих случаях q CU . Отношение зарядов при параллельU Ed ,
ном и последовательном подключении равно
qпар
qпосл
СпарU
СпослU
11.
Задача 18. Два плоских конденсатора имеют одинаковые заряды.
Емкость первого конденсатора в 2 раза больше емкости второго и
расстояние между пластинами у него в 1,5 раза больше. Найдите, во
сколько раз напряженность электрического поля в первом конденсаторе
меньше, чем во втором.
Решение. Поскольку заряды конденсаторов равны, равны и
произведения емкостей конденсаторов на напряжение q C1U1 C2U 2 .
11. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
Напряжение и напряженность поля E конденсатора связаны соотношением U Ed , где d - расстояние между пластинами конденсатора, тогдавыражение для заряда перепишется в виде 2C2 E1 1,5d2 C2 E2 d2 , отношение
напряженностей электрических полей в конденсаторах равно E2 3.
E1
Задача 19. В плоский воздушный конденсатор с расстоянием
между пластинами d = 6 мм ввели параллельно им пластину диэлектрика
толщиной d1 2 мм, lиэлектрическая проницаемость диэлектрика равна
e = 5, площадь пластин S=100 см 2. Найдите емкость такого конденсатора.
Решение. Пусть пластина из диэлектрика введена на расстоянии х
от нижней обкладки конденсатора, тогда верхняя поверхность пластины
находится на расстоянии d d1 x от его верхней обкладки. В результате
получаем последовательное соединение трех конденсаторов, суммарная
обратая величина емкости которых определяется формулой:
d d1
d
e(d d1 ) d1
1
1
1
1
1
.
С e0 S x e0 S d d1 x e0eS d1
e0 S
e0eS
e0eS
Тогда емкость конденсатора равна
C
e0 eS
20,1 пФ.
e(d d1 ) d1
12. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
Задача 20. К конденсатору емкостью 0,2 мкФ, заряженному донапряжения 100 В, параллельно подсоединили конденсатор емкостью 0,3
мкФ, заряженный до напряжения 50 В. Какой заряд перешел при этом
соединении с одного конденсатора на другой.
Решение. Начальный заряд первого конденсатора равен q1 C1U1, а
второго q2 C2U 2 . При параллельном соединении заряды на конденсаторах
перераспределяются так, чтобы напряжение на каждом из конденсаторов
стало одинаковым и равным U , тогда q q1 q2 C1U1 C2U 2 C1 C2 U ,
где C1 C2 - емкость при параллельном соединении. Напряжение U
равно U C1U1 C2U 2 . Заряд на каждом конденсаторе изменится на
C1 C2
одинаковую величину q . На первом конденсаторе он станет равным
C U C2U 2 C1C2 U1 U 2
'
q1' C1U , а q q1 q1 C1 U1 1 1
6 мкКл.
C
C
C1 C2
1
2











 Физика
Физика








