Похожие презентации:
Элементы квантовой физики. Лекция 6
1.
хТема: Элементы квантовой физики
1. Понятие о волновой функции
2. Уравнение Шредингера
3. Движение свободной частицы
4. Частица в одномерной прямоугольной
яме с бесконечными внешними «стенками»
6. Прохождение частиц сквозь
потенциальный барьер. Туннельный эффект
2.
х1. Понятие о волновой функции
Экспериментальное подтверждение идеи де Бройля об
универсальности
корпускулярно-волнового
дуализма
привели к новому этапу развития квантовой физики –
созданию квантовой механики, описывающей законы
движения и взаимодействия микрочастиц с учетом их
волновых свойств. Период с 1900 г. (формулировка Планком
квантовой гипотезы) до 20-х годов XX века.
3.
хНеобходимость вероятностного подхода к
описанию микрочастиц, является важнейшей
отличительной
особенностью
квантовой
теории.
4.
хнемецкий физик М. Борн в 1926 г.
предположил, что по волновому закону
меняется не сама вероятность, а величина,
названная
амплитудой
вероятности
и
обозначаемая
Ψ(х, y, z, t).
Эту величину называют также волновой
функцией (или Ψ – функцией).
Амплитуда вероятности может быть
комплексной, и вероятность W пропорциональна
квадрату ее модуля:
5.
хописание микрообъекта с помощью
волновой функции имеет статистический,
вероятностный характер:
квадрат модуля волновой функции
(квадрат модуля амплитуды волн де
Бройля)
определяет
вероятность
нахождения частицы в момент времени в
области с координатами x и dx, y и dy, z и
dz.
6.
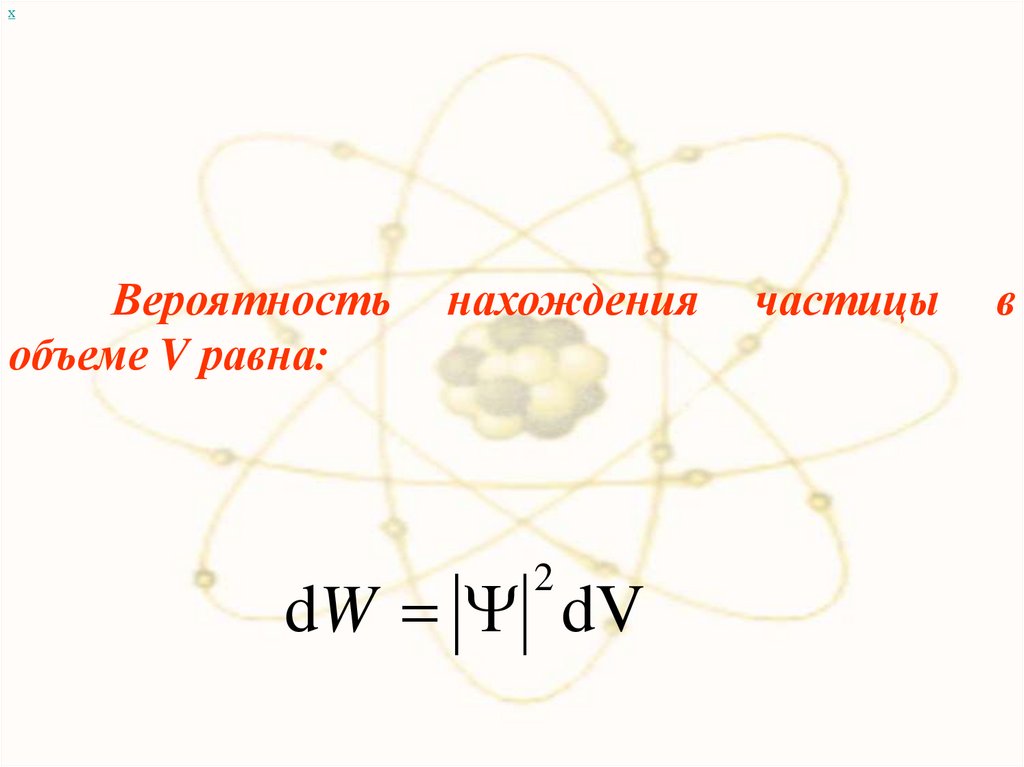
хВероятность
объеме V равна:
нахождения
dW dV
2
частицы
в
7.
хУсловия нормировки вероятностей:
| Ψ | dV 1,
2
где данный интеграл вычисляется по всему
бесконечному пространству, т.е. по координатам
x, y, z от –∞ до ∞.
Таким образом, условие нормировки говорит
об объективном существовании частицы во
времени и пространстве.
8.
V2
dV 1
9.
хЧтобы волновая функция являлась объективной
характеристикой состояния микрочастицы, она
должна удовлетворять ряду ограничительных
условий.
• конечной (вероятность не может быть больше
единицы);
• однозначной (вероятность не может быть
неоднозначной величиной);
• непрерывной (вероятность не может меняться
скачком).
10.
хВолновая функция удовлетворяет принципу
суперпозиции: если система может находиться
в
различных
состояниях,
описываемых
волновыми функциями Ψ1, Ψ2, … Ψn, то она
может находиться в состоянии, описываемом
линейной комбинацией этих функций
Ψ Cn Ψn
n
где Cn (n = 1, 2, 3…) – произвольные, комплексные
числа.
11.
хВолновая функция Ψ является основной
характеристикой состояния микрообъектов.
12.
х2. Уравнение Шредингера
Толкование волн де Бройля и соотношение
неопределенностей Гейзенберга привели к
выводу, что уравнением движения в квантовой
механике, описывающей движение микрочастиц в
различных силовых полях, должно быть
уравнение,
из
которого
бы
вытекали
наблюдаемые на опыте волновые свойства
частиц.
13.
хОсновное уравнение нерелятивистской
квантовой механики сформулировано в 1926 г.
Э.Шредингером.
14.
хУравнение Шредингера
записывается так:
в
общем
виде
2
U ( x , y , z , t ) i 2 ,
2m
t
2
2
h
где
- постоянная Планка,
2π
2
– оператор Лапласа
i – мнимая единица,
U(x, y, z, t) – потенциальная функция частицы в
силовом поле, в котором она движется,
Ψ – искомая волновая функция.
m – масса частицы.
15.
хЕсли силовое поле, в котором движется
частица потенциально, то функция U не зависит
явно от времени и имеет смысл потенциальной
энергии.
16.
Уравнение Шредингера для стационарныхсостояний
2m
2 ( E U ) 0
2
Е - полная энергия электрона
U - потенциальная энергия
-волновая функция электрона
( x , y, z )
17.
хУравнение Шредингера для стационарных
состояний
2m
2 ( E U ) 0
2
можно переписать в виде:
H E
2
U H – оператор Гамильтона,
2m
равный сумме операторов
2
Гамильтониан является оператором энергии E.
18.
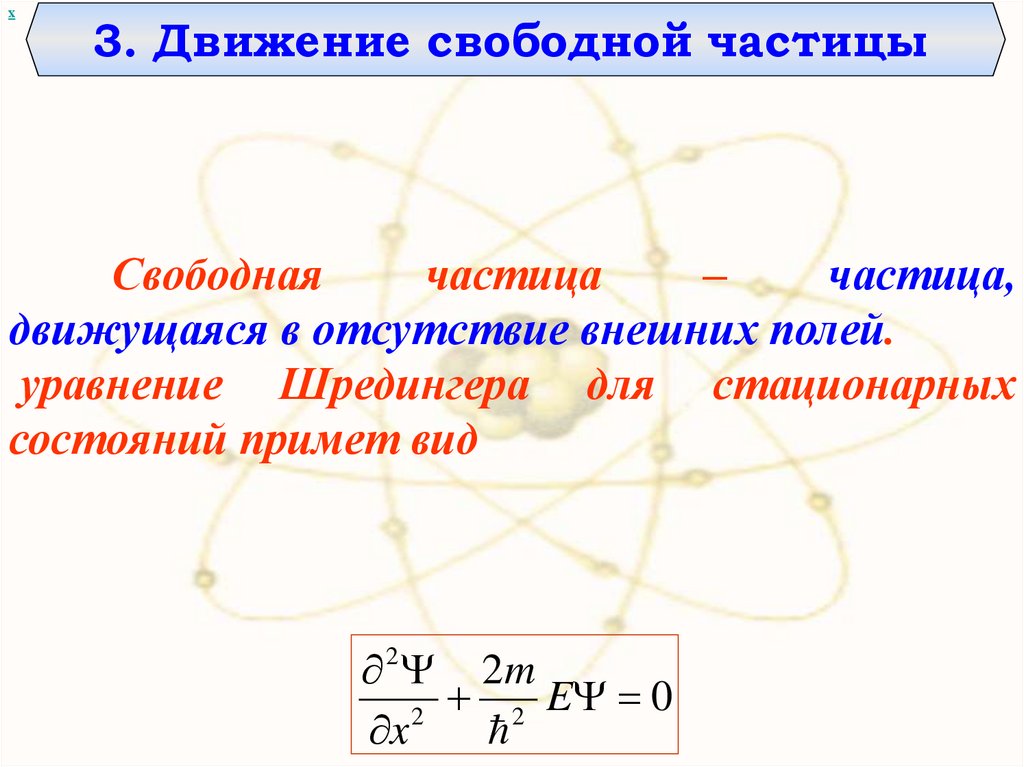
х3. Движение свободной частицы
Свободная
частица
–
частица,
движущаяся в отсутствие внешних полей.
уравнение Шредингера для стационарных
состояний примет вид
2m
2 E 0
2
x
2
19.
4. Частица в одномерной прямоугольнойяме с бесконечными внешними «стенками»
Проведем качественный анализ решений
уравнения Шредингера, применительно к
частице в яме с бесконечно высокими
«стенками».
20.
хТакая яма описывается потенциальной
энергией вида
, x 0
U ( x) 0, 0 x l
, x l
21.
хПо условию задачи (бесконечно высокие
«стенки»), частица не проникает за пределы
«ямы», поэтому вероятность ее обнаружения, (а
следовательно, и волновая функция) за
пределами «ямы» равна нулю.
(0) (l ) 0
(6)
22.
хВ пределах «ямы» (0 ≤ x ≤ l) уравнение
Шредингера (5) сведется к уравнению
2
k 0,
2
x
2
(7)
2mE
где k 2 .
2
Общее решение этого
дифференциального уравнения
( x) A sin kx
Уравнение Ψ(l) = A sin kl = 0 выполняется
только при
n
k
l
23.
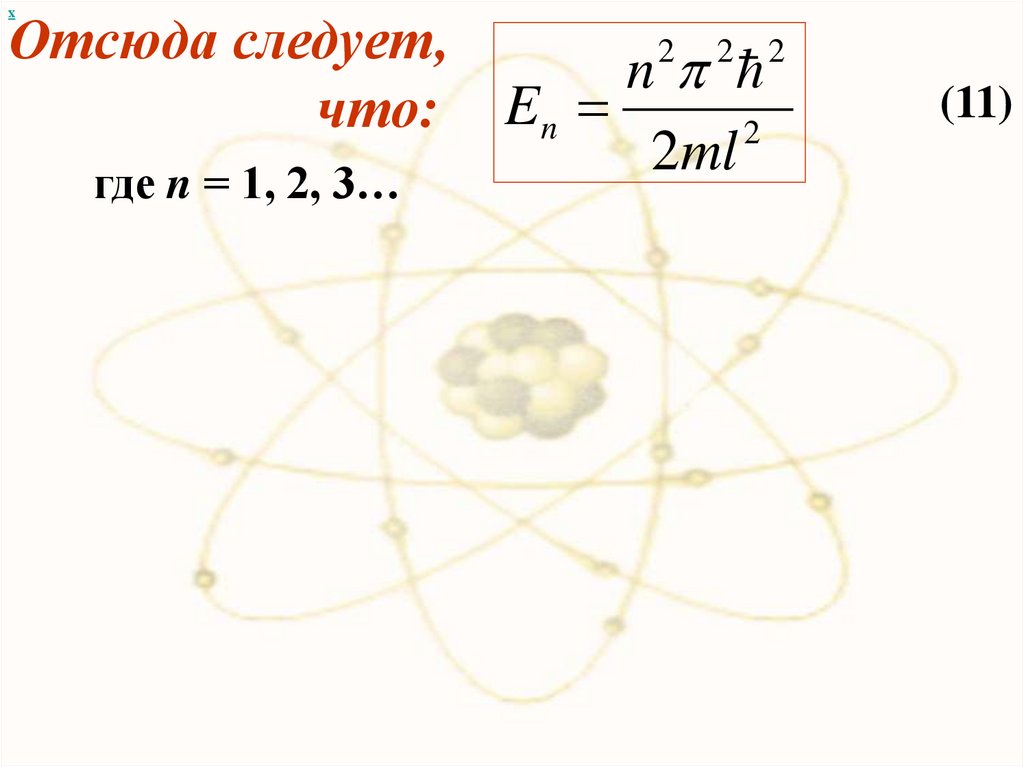
хОтсюда следует,
2 2 2
n
что: En
2
2ml
где n = 1, 2, 3…
(11)
24.
хКвантовые значения энергии En называется
уровнями энергии, а число п, определяющее
энергетические уровни - главным квантовым
числом.
25.
хСобственные функции будут иметь вид:
2 n
n ( x)
sin
x
l l
где n = 1, 2, 3…
26.
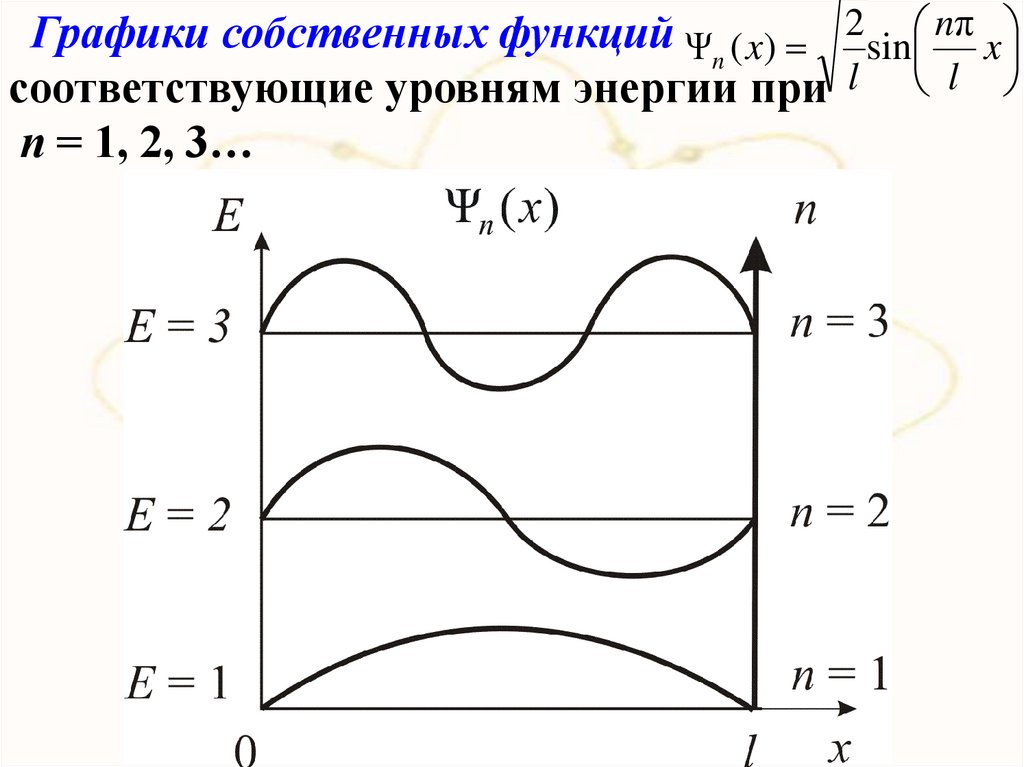
Графики собственных функций Ψn ( x) 2 sin nπ xсоответствующие уровням энергии при l l
п = 1, 2, 3…
27.
хВ
квантовом
состоянии с п = 2
частица не может
находиться в центре
ямы, в то время как
одинаково
может
пребывать в ее левой
и правой частях.
28.
хn
En
2
2ml
2
Из выражения
2
2
следует, что энергетический интервал между
двумя соседними условиями равен
Δ En En 1 En
2
ml
2
n
2
29.
хНеопределенность координаты Δx частицы в яме
шириной l равна Δx = l.
Тогда согласно соотношению неопределенностей,
х p
импульс не может иметь точное, в данном случае,
нулевое, значение. Неопределенность импульса:
Δp .
l
Такому разбросу значений импульса
соответствует минимальная кинетическая
2
2 2
энергия:
Δp
π
Emin
2m
2ml
2
30.
хпри бoльших квантовых числах n>>1
Δ En 2
1
En
n
т.е. соседние уровни расположены тесно: тем
теснее, чем больше п.
Если п очень велико, то можно говорить о
практически непрерывной последовательности
уровней и характерная особенность квантовых
процессов – дискретность – сглаживается.
частным случаем принципа соответствия Бора
(1923 г.)
31.
хПринцип соответствия:
всякая новая, более общая теория,
являющаяся развитием классической, не
отвергает ее полностью, а включает в себя
классическую теорию, указывая границы
ее применимости, причем в определенных
предельных условиях новая теория
переходит в старую.
32.
х5. Прохождение частиц сквозь
потенциальный барьер. Туннельный эффект
1 обл.
0, x 0
U ( x) U , 0 x 1 2 обл.
0, x 1
3 обл.
Рисунок 5
33.
хУравнение Шредингера для состояний в
каждой из выделенных областей имеет вид:
1,3
2
x
2
2mE
2
k 1,3 0 для1, 3 обл. k 2
2
2
2
q 2 0
2
x
2
2 m( E U )
2
для 2 обл. q
2
2m(U E )
.
Здесь q = iβ – мнимое число,β
Общее решение этих дифф. уравнений:
Ψ1 ( x) A1e B1e
ikx
ikx
(1)
Ψ2 ( x) A2 eikx B2 e ikx (2)
ikx
ikx
Ψ3 ( x) A3e B3e
(3)
34.
, квантовая механика приводит кпринципиально новому квантовому
явлению туннельному эффекту,
в результате которого микрообъект
может пройти через барьер.
35.
хКоэффициент прозрачности для барьера
прямоугольной формы
2
D D0exp
2m(U E )l
Для барьера произвольной формы
2 x2
D D0exp 2m(U E )l dx
x
1
36.
хПрохождение частицы сквозь ,барьер
можно
пояснить
соотношением
неопределенностей: х p
Неопределенность импульса на отрезке Δx = l
составляет
p .
l
Связанная с этим разбросом в значении
импульса
p 2
кинетическая энергия Ê
2m
может оказаться достаточной для того,
чтобы полная энергия оказалась больше
потенциальной.
37.
С классической точки зрения прохождениечастицы сквозь потенциальный барьер при
E < U невозможно, так как частица, находясь в
области барьера, должна была бы обладать
отрицательной кинетической энергией.
Туннельный эффект является специфическим
квантовым эффектом.
38.
Основы теории туннельных переходовзаложены работами
советских ученых
Л.И. Мандельштама и М.А. Леонтовича в 1928 г.
Туннельное
прохождение
сквозь
потенциальный барьер лежит в основе многих
явлений:
физики твердого тела (например, явления
в контактном слое на границе двух
полупроводников),
атомной и ядерной физики
(например, α-распад, протекание термоядерных
реакций).






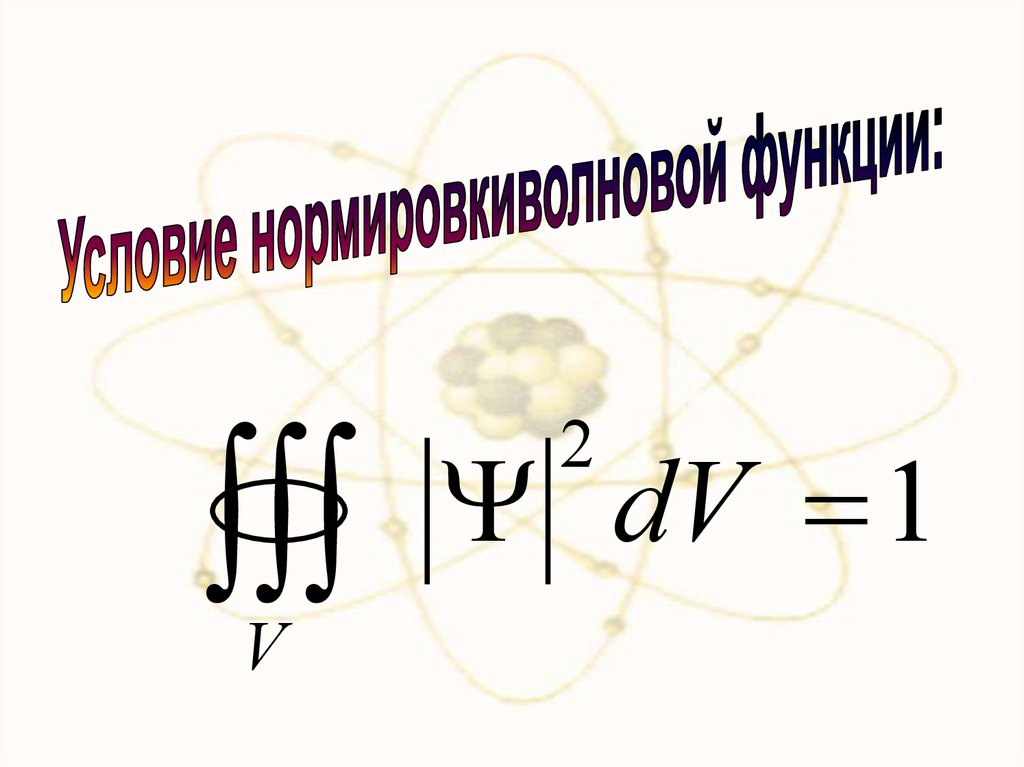


























 Физика
Физика








