Похожие презентации:
Квантовая физика. Состояние квантово-механической частицы
1.
Физика. 2 курс. 4 семестрСпециалитет
Лекция 2. Квантовая физика
Состояние квантово-механической
частицы:
- Свободная частица
- Частица в потенциальной «яме»
В.И. Читайкин
кандидат физико-математических наук
доцент
2.
План лекцииНаименование раздела, параграфа
Номер слайда
Введение
3
Раздел 1. Свободная частица
4
1.1. Основные понятия
5
1.2. Постановка задачи
6
1.3. Решение и следствия
7
Раздел 2. Частица в потенциальной «яме»
9
2.1. Основные понятия
10
2.2. Постановка задачи
13
2.3. Решение в общем виде
14
2.4. Роль граничных условий
15
2.5. О квантовании
16
2.6. Собственные значения энергии. Энергетический спектр
17
2.7. Собственные волновые функции
18
2.8. «Положение» частицы
19
2.9. Графическое представление
20
2
3.
ВведениеВ 1-ой лекции нашего курса была прослежена логика возникновения и развития квантовой
физики. Вкратце, она такова:
1. Признание корпускулярно-волнового дуализма («частица-волна» или «волна-частица») в
качестве фундаментального свойства вещества на микроуровне.
Луи д’Бройль
2. Понимание, что положение микрочастицы можно описать только вероятностным образом,
причём, сама вероятность W определяется через некоторую волновую функцию Ψ : W ~ │Ψ(x,y,z,t)│2.
При этом эта волновая функция обладает странным для физики свойством: она принципиально
ненаблюдаема, призрачна.
Макс Борн
3. Формулирование дифференциального уравнения Шредингера, позволяющего рассчитывать
волновую функцию и на её основе – определять «положение» частицы, энергию и другие параметры.
Само уравнение было «взято» de capite (из головы).
Эрвин Шредингер
Во 2-ой и последующих лекциях рассматриваются решения уравнения Шредингера для ряда
практически важных случаев. Рассмотрение ведётся последовательно, по мере усложнения.
Полученные результаты позволяют выявить полезные физические эффекты и понятия.
Важно, что сам процесс решения уравнения Шредингера и его результаты позволят прояснить
суть понятия «квантования», введённого в предыдущей лекции.
Рассмотрение будет проводиться для стационарных условий и для одномерного случая.
3
4.
Раздел 1. Свободная частица4
5.
1. Свободная частица1.1. Основные понятия
1. Свободная частица – это частица, которая находится вне какого-либо внешнего
потенциального поля: гравитационного, электростатического, магнитного, ядерного. То есть нет
никакого взаимодействия частицы с полем, значит, нет и потенциальной энергии такого
взаимодействия. Поэтому в уравнении Шредингера параметр U, играющий роль потенциальной
энергии, равен 0.
На «свободную» от взаимодействия частицу не действует никакая сила, т.к.
F = – grad U = – grad 0 = 0.
Но отсутствие взаимодействия не означает, что свободная частица не может обладать энергией.
Будем считать, частице сообщили (задали откуда-то извне) энергию Е = Const.
2. Определить состояние свободной частицы – это означает найти «положение» частицы в
пространстве при заданном значении энергии Е.
Ради физической ясности и математической простоты будем рассматривать:
- стационарные состояния свободной частицы, когда её «положение» в пространстве не меняется
во времени, значит, частица остаётся неподвижной.
- одномерное пространство: -∞ < х < +∞.
5
6.
1. Свободная частица1.2. Постановка задачи
Частица, обладающая энергией Е и массой m, находится в одномерном пространстве свободно, т.е. в
отсутствии внешних силовых полей: U(x) = 0. Значение Е может быть любым.
Требуется найти «положение» частицы, что на квантово-механическом языке означает: нужно
определить вероятность W нахождения частицы в какой-либо точке пространства х.
В квантовой физике вероятность рассчитывается через волновую функцию: W ~ Ψ2 = Ψ ∙Ψ * , значит,
надо найти волновую функцию («пси-функцию»).
По условию (см. предыдущий слайд), волновая функция:
- не изменяется во времени: dΨ / dt = 0;
- есть функция только координаты х: Ψ(x).
Для нахождения волновой функции нужно решить стационарное уравнение Шредингера:
ℏ = h/2π, h – постоянная Планка
В результате решения стационарного уравнения Шредингера может быть найдена пси-функция Ψ(х)
для заданного значения энергии Е и, вслед за этим, будет определена вероятность нахождения частицы в
точке х: W(x) ~ Ψ2 (х).
Обратите внимание, вероятность не равна Ψ2 (х), а пропорциональна (знак ~). Вспомните, почему?
6
7.
1. Свободная частица1.3. Решение и следствия
Повторим уравнение Шредингера для заданных условий:
Решение этого уравнения: Ψ(х) = А∙cos(k∙x) или: Ψ(х) = А∙ еikx (вспомните теорию функций комплексной
переменной; напишите, как связаны оба
представления Ψ(х) )
Это – плоская, т.к. одномерная, монохроматическая волна д’Бройля, которая соответствует
частице массой m и энергией Е или импульсом p = √(2mE) .
- волновой вектор (волновое число), вектор
- длина волны д’Бройля, скаляр
С очень высокой степенью условности, можно
поставить в соответствие друг другу «наглядные
образы» частицы и волны д‘Бройля:
х
7
8.
1. Свободная частица1.3. Решение и следствия (продолжение)
Следствие 1: Все положения свободной квантовой частицы в пространстве равновероятны,
вероятность обнаружить частицу в любой точке пространства одинакова.
Действительно, вероятность нахождения частицы в произвольной точке пространства:
W ~ Ψ2 = Ψ ∙Ψ * . Для свободной частицы W = A2, т.е. зависимости от координат нет. Покажите это.
Следствие 2: Для свободной частицы энергетический спектр – непрерывен, все значения энергии Е
разрешены (как в классической механике).
Действительно, решение уравнения Шредингера Ψ(х) = А∙cos(k∙x) не накладывает никаких
ограничений на значение волнового числа k, оно может быть любым.
Т.к. волновое число k однозначно связано с импульсом р и энергией Е частицы:
p = k∙ℏ,
E = p2/2m = k2∙ℏ2/2m, –
то импульс р и энергия Е могут также принимать любые, в том числе, сколь угодно близкие
значения, т.е. быть непрерывными.
Важный вывод: решение уравнения Шредингера (а это и есть сам процесс квантования!) не
привело к появлению дискретных значений энергии, импульса, координат свободной частицы.
Квантовые, т.е. дискретные, состояния у свободной частицы отсутствуют.
8
9.
Раздел 2. Частица в потенциальной «яме»9
10.
2. Частица в потенциальной «яме»2.1. Основные понятия
Состояние несвободной частицы кардинально отличается от состояния свободной частицы.
Несвободная частица так же, как свободная, находится в пространстве, но в отличие от случая со
свободной частицей, в пространстве имеются внешние потенциальные поля, действующие на частицу.
Т.е. потенциальная энергия частицы во внешнем поле не равна нулю: U ≠ 0.
Уравнение Шредингера для этого случая можно записать так (см. предыдущую лекцию):
Е – полная энергия частицы,
U – потенциальная энергия частицы.
-
Отличие состояний несвободной и свободной частиц состоит также в следующем:
на несвободную частицу действуют внешние силы: F = -gradU(х) ≠ 0;
в случае свободной частицы внешних сил нет: F = 0.
10
11.
2. Частица в потенциальной «яме»2.1. Основные понятия (продолжение)
Зависимость потенциальной энергии от координат может быть различной, соответствующей конкретной задаче. Это чаще всего делает невозможным аналитическое решение уравнения Шредингера.
Требуются развитые численные методы и современные супер ЭВМ. Это – предмет вычислительной
квантовой физики (и химии).
Для анализа принципиальных особенностей поведения волновой функции используются простые
зависимости потенциальной энергии от координат. Наибольший практический смысл имеет зависимость
U(x) в виде потенциальной «ямы» – см. рисунок.
Параметры потенциальной ямы («форма», глубина, максимальное значение) не зависят от энергии рассматриваемой частицы Е, они определяются другими частицами, внешними по отношению к «нашей» частице.
Частица, обладающая полной энергией Е, может находиться только в
той области пространства, где величина E – U ≥ 0, или E ≥ U . За этими
пределами частица находиться не может, «не хватает энергии»: Е < U.
Разрешённая область пространства это: х1 ≤ х ≤ х2. «Частица находится в
Энергия
U(x)
потенциальной яме».
Разрешённая область
Но в случае потенциальной ямы произвольной формы решение уравнения Шредингера остаётся весьма затруднительным.
11
12.
2. Частица в потенциальной «яме»2.1. Основные понятия (продолжение)
Изучать принципиальные особенности состояния квантовых частиц следует начать с простейшего
вида зависимости потенциальной энергии от координат U(x), а именно: потенциальная «яма» с
бесконечными вертикальными стенками.
х
Потенциальная «яма»
с бесконечными стенками
Левая, бесконечно высокая стенка «ямы» помещена в начало
координат: х1 = 0.
Правая, также бесконечно высокая стенка «ямы» находится в
точке х2 = l.
l – ширина «ямы».
Внутри «ямы» внешнее потенциальное поле отсутствует
U = 0, т.е. на частицу внутри «ямы» не действуют никакие
силы.
12
13.
2. Частица в потенциальной «яме»2.2. Постановка задачи
Сформулируем задачу в строгой постановке.
Частица, обладающая энергией Е и массой m, находится в
ограниченной области пространства x = [0, l].
Внутри этой области потенциал U=0.
За пределами этой области U(x≤0) = U(x≥l) = ∞.
Понятно, что частица не может существовать вне области x = [0, l], т.к.
при любом конечном значении энергии будет выполнено условие Е < U = ∞.
х
Потенциальная «яма»
с бесконечными стенками
Иногда говорят так: частица «заперта в прямоугольном ящике (или яме)».
Для поиска решения дифференциального уравнения необходимо знать граничные условия, т.е.
условия на границах «ямы».
Из свойства непрерывности волновой функции (см. предыдущую лекцию) следует, что на границах
«ямы» решение уравнения должно удовлетворять следующим граничным условиям:
Ψ(x=0) = Ψ(x=l) = 0 .
Внутри «ямы» частица, казалось бы, должна быть свободной (т.к. U = 0) и, значит, иметь
произвольные значения координаты, энергии, импульса и других параметров. Но это не так!
13
14.
2. Частица в потенциальной «яме»2.3. Решение в общем виде
Уравнение Шредингера относительно искомой волновой функции внутри потенциальной «ямы»,
где U=0, выглядит так:
Перепишем это уравнение, введя обозначение:
Общий вид решения уравнения внутри «ямы» таков:
Ψ(x) = А∙sin(k∙x + α)
при 0 ≤ х ≤ l
А и α – произвольные постоянные
Обратите внимание: в формуле используется функция синуса, а не косинуса, как это было в разделе 1. Решение
уравнения Шредингера допускает использование любой из этих двух функций, т.к. отличие синуса от косинуса
состоит только в сдвиге фазы (аргумента) на π/2, что легко учитывается в значении параметра α.
Выбор синуса или косинуса зависит от удобства решения конкретной задачи.
14
15.
2. Частица в потенциальной «яме»2.4. Роль граничных условий
Найденная волновая функция (см. предыдущий слайд) должна удовлетворять граничным условиям для
потенциальной «ямы» - см. слайд 13:
Ψ(x=0) = 0,
Ψ(x=l) = 0 .
Из граничного условия на левой границе (х=0) получим:
Ψ(x=0) = А∙sinα = 0, отсюда следует, что α = 0.
Если бы мы выбрали решение в виде Ψ(x) = А∙cos(k∙x + α),
то получили бы значение α = π/2, что несколько усложняет
вид формулы и последующий анализ.
Граничное условие на левой границе «ямы» выполняется при любом значении числа k.
Из граничного условия на правой границе (x=l) получим:
Ψ(х=l) = А∙sin(k∙l) = 0, отсюда следует, что k∙l = ±n∙π, n = 1, 2, 3 …
Это условие означает, что на длине l должно укладываться целое число полупериодов волновой
функции.
Граничное условие на правой границе «ямы» накладывает жёсткое ограничение на значение числа k;
это число не может быть произвольным, оно дискретно: k = ±n∙π/ l, n = 1, 2, 3 …
Подумайте, почему исключено значение n = 0.
15
16.
2. Частица в потенциальной «яме»2.5. О квантовании
Процесс квантования – это решение уравнения Шредингера совместно с граничными условиями.
Можно сказать, что в предыдущих пунктах мы «проквантовали» частицу в бесконечной,
прямоугольной потенциальной «яме».
В результате такого квантования определяются дискретные, т.е. квантовые состояния частицы, или:
состояния системы – частицы и потенциального поля Ψ(х).
Действительно, значения числа k оказались дискретными (квантованными):
kn = ±n∙π/ l,
n = 1, 2, 3 …
Число k однозначно определяет энергию частицы Е (см. слайд 14), значит, значения энергии Е также
оказываются дискретными (квантованными):
Еn =
n = 1, 2, 3 …
Нетрудно видеть, что импульс частицы также оказывается квантованным, т.е. дискретным.
(Выполните это самостоятельно. Обратите внимание на ударение в слове «квантованный».)
16
17.
2. Частица в потенциальной «яме»2.6. Собственные значения энергии. Энергетический спектр
Собственные значения энергии частицы – это такие значения энергии Е, которые удовлетворяют
уравнению Шредингера совместно с граничными условиями.
Для рассмотренного случая частицы в бесконечной, прямоугольной потенциальной «яме»
собственные значения энергии частицы дискретны:
Еn =
, упрощенно: Еn ~ n2
n = 1, 2, 3 ….
Взаимное расположение собственных энергетических уровней частицы в
потенциальной «яме» схематически показано на рисунке справа.
n – номер собственного энергетического дискретного уровня, главное
квантовое число. Значение n определяет энергию частицы в заданном поле U(x).
Последовательность собственных значений энергии частицы называется
энергетическим спектром. Минимальное значение энергии частицы достигается при n=1, оно всегда больше нуля (Е1 > 0)!
Принципиально, что частица с промежуточным значением энергии, т.е. с энергией между
соседними дискретными энергетическими уровнями, существовать не может.
l
17
18.
2. Частица в потенциальной «яме»2.7. Собственные волновые функции
Собственным значениям энергии Еn соответствуют собственные волновые функции Ψn (вспоминайте
матанализ). Общий вид такой функции в прямоугольном потенциале с бесконечными стенками («яме») таков:
Ψn(x) = А∙sin(kn∙x + α)
Напомню, волновое число k имеет дискретные значения kn
После учёта граничных условий было получено, что α = 0. Т.е. общий вид собственной волновой
функции упростился:
Ψn(x) = А∙sin(kn∙x) .
Для определения коэффициента А надо воспользоваться условием нормировки волновых функций:
∫ [Ψn (x)]2 dx = 1
Интеграл следует брать по всей ширине «ямы»: x = [0, l] и для каждого значения n в отдельности.
После выполнения интегрирования и несложных алгебраических преобразований получим:
А = √2 / l .
Важно: амплитуда не зависит от квантового числа n.
В итоге, собственная волновая функция частицы в «яме» имеет следующий вид:
Ψn(x) = √2 / l ∙ sin(nπx / l).
Укажите размерность волновой функции? Объясните смысл полученной
размерности?
Будет весьма полезным, если Вы самостоятельно получите формулу, связывающую собственную волновую функцию Ψn(x) с
собственными значениями энергии Еn. Подсказка: надо использовать формулу kn = f(En).
18
19.
2. Частица в потенциальной «яме»2.8. «Положение» частицы
Последним этапом решения уравнения Шредингера является определение «положения» частицы в
потенциальной «яме». Следует иметь в виду, что «положение» частицы понимается как вероятность
нахождения частицы в определённой точке, но не как факт нахождения частицы в этой точке.
Напомню, вероятность, точнее, плотность вероятности Р, рассчитывается как квадрат
соответствующей волновой функции:
Р = dW(х) / dх = [Ψn(х)]2 .
Подставим в эту формулу полученное ранее выражение для Ψn(х) – см. предыдущий слайд. Получим:
Р = dW(х) / dх = (2 / l)∙sin2(nπx / l),
n = 1, 2, 3 ….
Тогда собственно вероятность нахождения частицы в интересующем нас интервале [x1, x2] есть:
W(x1 ≤ х ≤ x2) = ∫ [Ψn(х)]2 dx, пределы интегрирования по х: от x1 до x2; т.е. по границам интервала.
Какая размерность dW(х) ?
Важно!
- Значения вероятности W и плотности вероятности Р всегда больше или равны 0.
- Значения волновой функции, как правило, знакопеременны: Ψn(х) может быть больше и меньше
нуля, может быть равна нулю. Напомню, волновая функция принципиально ненаблюдаема, поэтому
отрицательные значения для волновой функции возможны.
19
20.
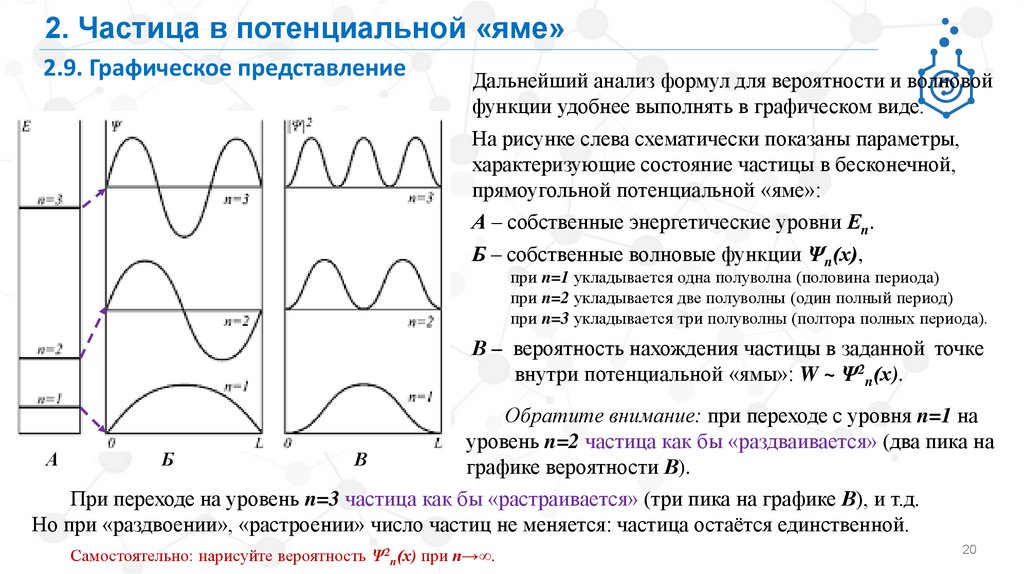
2. Частица в потенциальной «яме»2.9. Графическое представление
Дальнейший анализ формул для вероятности и волновой
функции удобнее выполнять в графическом виде.
На рисунке слева схематически показаны параметры,
характеризующие состояние частицы в бесконечной,
прямоугольной потенциальной «яме»:
А – собственные энергетические уровни Еn.
Б – собственные волновые функции Ψn(х),
при n=1 укладывается одна полуволна (половина периода)
при n=2 укладывается две полуволны (один полный период)
при n=3 укладывается три полуволны (полтора полных периода).
В – вероятность нахождения частицы в заданной точке
внутри потенциальной «ямы»: W ~ Ψ2n(х).
Обратите внимание: при переходе с уровня n=1 на
уровень n=2 частица как бы «раздваивается» (два пика на
А
Б
В
графике вероятности В).
При переходе на уровень n=3 частица как бы «растраивается» (три пика на графике В), и т.д.
Но при «раздвоении», «растроении» число частиц не меняется: частица остаётся единственной.
Самостоятельно: нарисуйте вероятность Ψ2n(х) при n→∞.
20




















 Физика
Физика








