Теория вероятностей

1. Теория

вероятностей

2.

«Теория вероятностей»
Что это такое?
Задачи любой науки состоят в выявлении и исследовании
закономерностей, которым подчиняются реальные
процессы.
Теория вероятностей – математическая наука,
изучающая закономерности случайных явлений.
Знание закономерностей, которым подчиняются массовые
случайные события, позволяет предвидеть, как эти события
будут протекать.
Методы теории вероятностей широко применяются в
различных отраслях науки и техники: в теории надёжности,
теории массового обслуживания, теоретической физике,
астрономии, теории ошибок, теории управления, теории
связи и во многих других теоретических и прикладных
науках.
Теория вероятностей служит для обоснования
математической статистики.

3.

«Теория вероятностей»
Справочные материалы
Классическое определение вероятности:
Вероятностью события А называется отношение числа
благоприятных для него исходов испытания к числу всех
равновозможных исходов.
где m - число исходов, благоприятствующих
осуществлению события,
а n - число всех возможных исходов.

4.

«Теория вероятностей»
Справочные материалы
Основные понятия теории вероятностей:
Наблюдаемые события можно разделить на три вида: достоверные,
невозможные и случайные.
• Событие называется достоверным, если оно обязательно
произойдет при выполнении данного ряда условий.
Например: При подбрасывании игрального кубика выпадет число
меньшее 7.
• Событие называется невозможным, если оно заведомо не
произойдет при выполнении данного ряда условий.
Например: При подбрасывании игрального кубика выпадет число 7.
• Событие называется случайным, если при осуществлении ряда
условий оно может либо произойти, либо не
произойти.
Например: При подбрасывании игрального кубика
выпадет число 6.

5.

«Теория вероятностей»
Справочные материалы
Некоторые свойства :
а) вероятность достоверного события равна единице;
б) вероятность невозможного события равна нулю;
в) вероятность случайного события есть положительное число,
заключенное между нулем и единицей;
г) вероятность суммы двух несовместных событий равна сумме
вероятностей этих событий: P(A + B) = P(A) + P(B).

6.

«Теория вероятностей»
Задание № 1. Исследуй виды событий.
1. ночью светит солнце
2. 1 января – праздничный день
3. в полночь выпадет снег, а через 24 часа будет светить солнце
4. футбольный матч «Спартак» - «Динамо» закончится вничью
5. при броске монеты выпал «орел»
6. при броске игрального кубика выпало 9 очков
7. при телефонном звонке абонент оказался занят
8. сосна зимой зеленая
9. бутерброд на завтрак будет с маслом
10. черепаха научится говорить
11. 30 февраля будет дождь
12. летом у школьников будут каникулы
13. вы выходите на улицу, а
навстречу вам идет динозавр
14. после четверга будет пятница

7.

«Теория вероятностей»
Схема решения задач на применение
формулы вероятности:
1. Внимательно прочитайте задачу, выделите, что именно
происходит (бросается игральный кубик, что из какого
ящика вытаскивается и др.).
2. Найдите основной вопрос задачи: «Вычислить (найти)
вероятность того, что…», определите «А – событие, что…»
3. Определите число всех возможных исходов – n.
4. Определите число благоприятных событий – m.
5. Составьте отношение m к n.
6. Найдите значение отношения – Р(А).
7. Запишите ответ.

8.

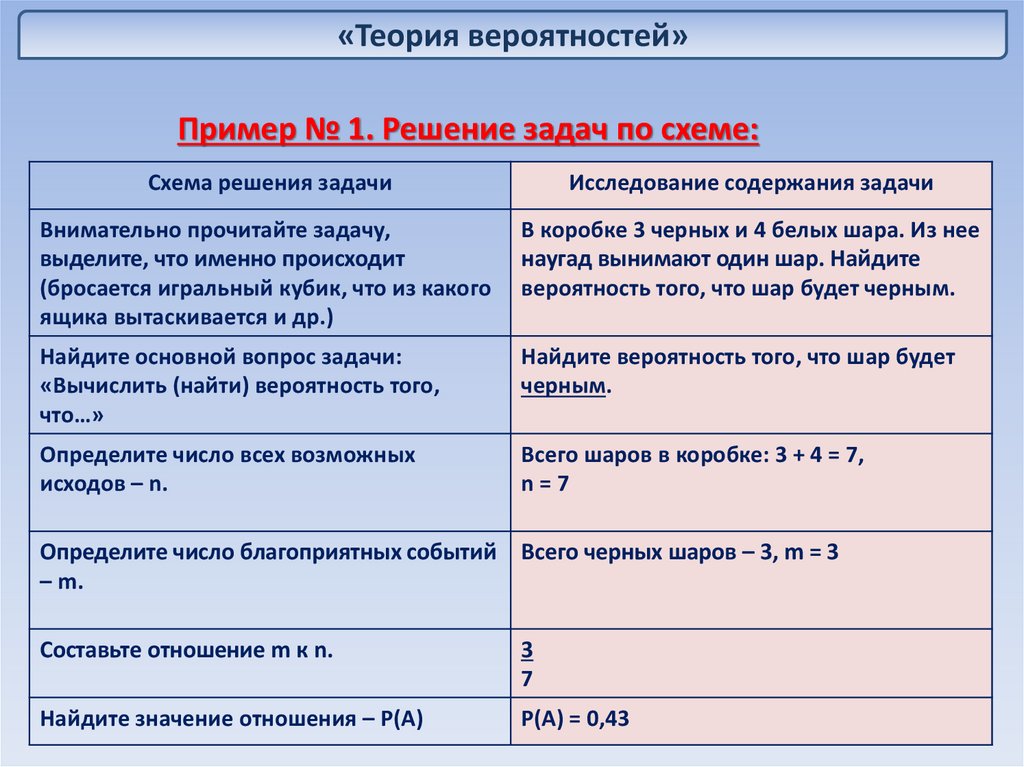
«Теория вероятностей»
Пример № 1. Решение задач по схеме:
Схема решения задачи
Исследование содержания задачи
Внимательно прочитайте задачу,
выделите, что именно происходит
(бросается игральный кубик, что из какого
ящика вытаскивается и др.)
В коробке 3 черных и 4 белых шара. Из нее
наугад вынимают один шар. Найдите
вероятность того, что шар будет черным.
Найдите основной вопрос задачи:
«Вычислить (найти) вероятность того,
что…»
Найдите вероятность того, что шар будет
черным.
Определите число всех возможных
исходов – n.
Всего шаров в коробке: 3 + 4 = 7,
n=7
Определите число благоприятных событий Всего черных шаров – 3, m = 3
– m.
Составьте отношение m к n.
3
7
Найдите значение отношения – Р(А)
Р(А) = 0,43

9.

«Теория вероятностей»
Пример № 2. Решение задач по схеме:
Схема решения задачи
Исследование содержания задачи
Внимательно прочитайте задачу, выделите,
что именно происходит (бросается
игральный кубик, что из какого ящика
вытаскивается и др.)
На полке стоят 3 синих, 2 зеленых, 5
красных книги. Вычислите вероятность того,
что Вера возьмет с полки красную книгу.
Найдите основной вопрос задачи:
«Вычислить (найти) вероятность того, что…»
Вычислите вероятность того, что Вера
возьмет с полки красную книгу.
Определите число всех возможных исходов
– n.
Всего книг на полке: 3 + 2 + 5 = 10,
n = 10
Определите число благоприятных событий
– m.
Всего красных книг на полке – 5, m = 5
Составьте отношение m к n.
5
10
Найдите значение отношения – Р(А)
Р(А) = 0,5

10.

«Теория вероятностей»
Решение задач по формуле: Р(А) =
Пример 1
Коля, Ваня, Петя, Вася бросили жребий – кому идти в
магазин. Найдите вероятность того, что в магазин пойдет
Петя.
Решение:
А – событие, что в магазин пойдет Петя.
n = 4 – число всех возможных исходов –
всего мальчиков
m = 1 – число благоприятных исходов жребий выпал на Петю
Р(А) =
=
= 0,25
Ответ: 0,25

11.

«Теория вероятностей»
Решение задач по формуле: Р(А) =
Пример 2
13 учащихся девятого класса пришли в школу в костюмах,
четверо в футболках, пятеро в свитерах, трое в рубашках.
Какова вероятность того, что случайно выбранный ученик
девятого класса пришел в школу в футболке?
Решение:
А – событие, что ученик пришел в футболке.
n = 13 + 4 + 5 + 3 = 25 – число всех возможных исходоввсего учеников девятого класса
m = 4 – число благоприятных исходов всего учеников, которые пришли в футболках
Р(А) =
=
= 0,16
Ответ: 0,16

12.

«Теория вероятностей»
Решение задач по формуле: Р(А) =
Пример 3
Соревнования проводятся в 5 дней. Всего заявлено 80 команд
(по одной от каждой страны). В первый день соревнуются 8 команд,
остальные распределены поровну между оставшимися днями.
Порядок соревнований определяется жеребьёвкой. Какова
вероятность, что команда из России примет участие в третий день
соревнований? Решение:
А – событие, что команда из России примет участие в третий день
соревнований.
n = 80 – число всех возможных исходов – всего выступлений
m = (80 – 8) : 4 = 18 –число благоприятных исходовпорядковых номеров, приходящихся на второй, третий,
четвертый и пятый дни
Р(А) =
=
= 0,225
Ответ: 0,225

13.

«Теория вероятностей»
Решение задач по формуле: Р(А) =
Пример 4
В чемпионате мира участвуют 20 команд. С помощью жребия их нужно
разделить на четыре группы по пять команд в каждой. В ящике
вперемешку лежат карточки с номерами групп: 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3
4 4 4 4 4 . Капитаны команд тянут по карточке. Какова вероятность того,
что команда Великобритании окажется во второй группе?
Решение:
А – событие, что команда Великобритании окажется во
второй группе.
n = 20 – число всех возможных исходов – всего карточек
m = 5 – число благоприятных исходов-число карточек с
номером 2
Р(А) =
=
= 0,25
Ответ: 0,25

14.

«Теория вероятностей»
Решение задач по формуле: Р(А) =
Пример 5
Какова вероятность того, что при бросании игрального
кубика выпадает число очков, больше 4?
Решение:
А – событие, что выпадает число очков, больше 4.
n = 6 – число всех возможных исходов –
это 1, 2, 3, 4, 5, 6
m = 2– число благоприятных исходовэто 5 и 6, т.к. эти числа больше 4
Р(А) =
=
≈ 0,33
Ответ: 0,33

15.

«Теория вероятностей»
Решение задач по формуле: Р(А) =
Пример 6
Алеша наудачу выбирает двузначное число. Найдите
вероятность того, что оно оканчивается на 0.
Решение:
А – событие, что число оканчивается на 0.
n = 90 – число всех возможных исходов –
всего двузначных чисел 90
m = 9 – число благоприятных исходов- всего
двузначных чисел, которые оканчиваются на 0 – это 10,
20,…, 90
Р(А) =
=
= 0,1
Ответ: 0,1

16.

«Теория вероятностей»
Решение задач по формуле: Р(А) =
Пример 7 В случайном эксперименте симметричную
монету бросают трижды. Найдите вероятность того,
что орел выпадет все три раза.
Решение:
Количество разных вариантов бросания одной монеты трижды
следующие: ООО, РРР, ОРО, РОР, ОРР, РРО, ООР, РОО, тогда
А – событие, что орел выпадет все три раза.
n = 8 – число всех возможных исходов –
всего вариантов бросания монеты
m = 1 – число благоприятных исходов –
всего подряд выпадет ООО
Р(А) =
=
= 0,125
Ответ: 0,125