Пример записи решения задания к Части I РГР №1

1. Пример записи решения задания к Части I РГР №1

ПРИМЕР ЗАПИСИ РЕШЕНИЯ ЗАДАНИЯ
К ЧАСТИ I РГР №1
Задание: По данным выборки:
1. Составить дискретный вариационный ряд.
2. Построить полигон.
3. Найти средние характеристики:
а) среднее выборочное x ;
б) моду M 0 ;
в) медиану me .
4. Найти характеристики вариации:
а) размах вариации X R ;
б) дисперсию D;
в) среднее квадратическое отклонение ;
г) коэффициент вариации V;
д) ошибку выборочного среднего .
5. Сделать вывод.
43
45
46
47
46
Исходные данные:
Число отжиманий в упоре лежа
46 45 43 44 45 47 43 44
44 42 45 47 44 46 46 46
43 44 47 45 46 42 44 44
45 46 46 48 45 45 43 45
44 45
46
43
46
47

2.

Этапы выполнения:
1.Cоставим дискретный вариационный ряд
Все варианты расположим в порядке
возрастания в первой строке таблицы, а
частоту, с которой они встречаются в данной
выборке во второй строке.
xi
42
43
44
45
46
47
48
ni
2
6
8
10
11
5
1
Объем выборки n=43.

3.

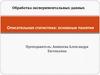
2. Построим полигон
Для построения полигона на оси OX отложим
значения вариант xi, а на оси OY –
значения частот ni. xi 42 43 44 45 46 47 48
ni
ni
12
2
6
8
10
11
10
8
6
4
2
0
41
42
43
44
45
46
47
48
49
xi
5
1

4.

3. Вычислим средние характеристики
xi 42 43 44 45n 46 47
а) Определим среднее выборочное
:
1
x
xi ni
ni 2
6
8 n10i 1 11 5
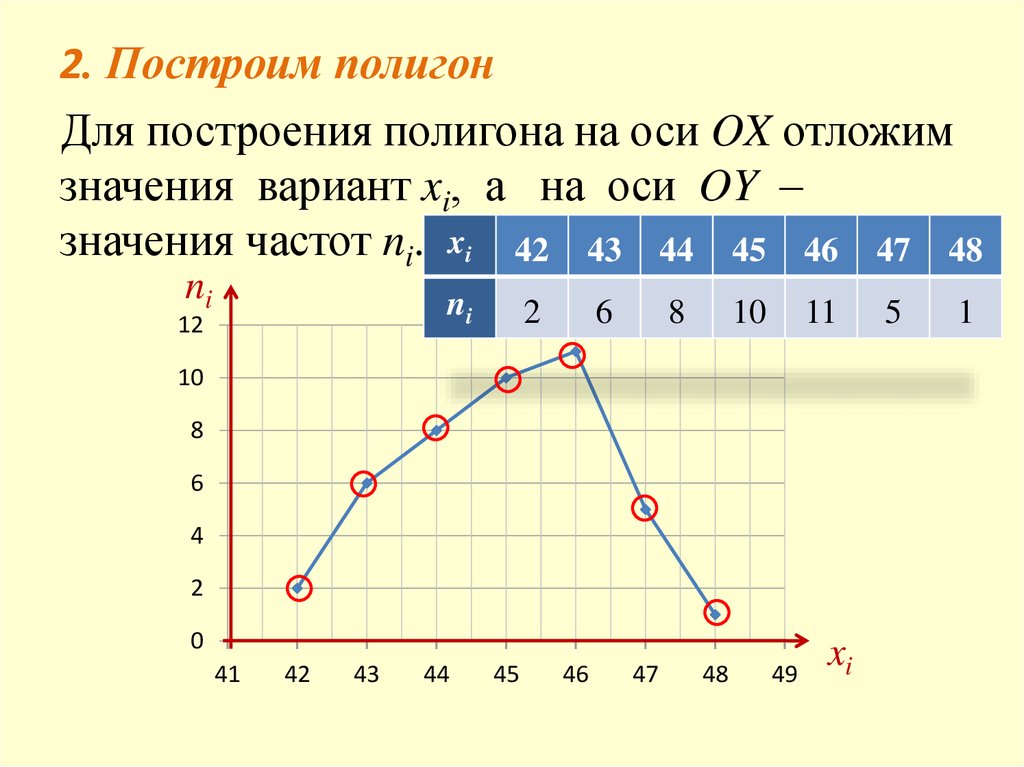
Вычисления оформим в виде таблицы:
xi
ni
xi ∙ni
42
43
44
45
46
47
48
2
6
8
10
11
5
1
84
258
352
450
506
235
48
=1933
1
x 1933 44,953 45
43
48
1

5.

б) Определим моду:
xi
42
43
44
45
46
47
48
ni
2
6
8
10
11
5
1
M 0 46

6.

в) Определим медиану :
Выборку сначала необходимо проранжировать:
42
44
45
46
47
42
44
45
46
47
43
44
45
46
48
43
44
45
46
43
44
45
46
43
44
45
46
43
45
46
46
43
45
46
47
44
45
46
47
44
45
46
47
Объем выборки n=43 является нечетным числом,
следовательно me xk 1 , где k n 1 .
43 1
21 ,
2
2
Значит,
то есть me x21 1 x22
22-ой по счету вариант в ранжированном ряду и будет
медианой:
k
me x22 45

7.

4. Вычислим характеристики вариации
а) Определим размах вариации :
X R xmax x
min
xmin 42
xmax 48
X R 48 42 6

8.

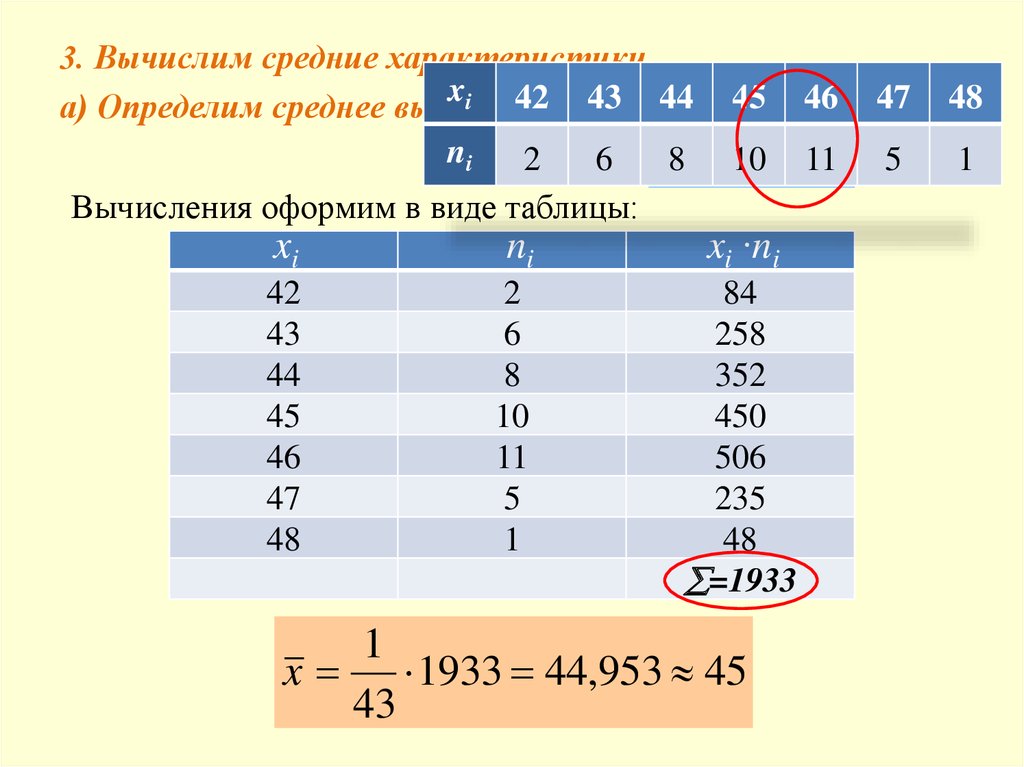
б) Определим дисперсию:
1 n
D ( xi x ) 2 ni
n i 1
Вычисления оформим в виде таблицы:
xi
ni
42
43
44
45
46
47
48
2
6
8
10
11
5
1
-3
-2
-1
0
1
2
3
9
4
1
0
1
4
9
1
D 90 2,09
43
18
24
8
0
11
20
9
=90
x 45

9.

в) Определим среднее квадратическое отклонение:
D
2,09 1,45

10.

г) Определим коэффициент вариации:
V
x
100%
1,45
V
100 % 0,032 100 % 3,2%
45

11.

д) Определим ошибку выборочного среднего:
Sx
n
1,45
Sx
0,22
43

12.

5. Вывод. По данным числа отжиманий в упоре
лежа 43 испытуемых средний результат составил
45 раз ± 0 раз. Степень рассеяния данных
выборки от среднего результата составляет 1
отжимание. Чаще всего встречаемый результат в
группе – 46 отжиманий. Одна половина
спортсменов показала результаты лучше 45
отжиманий, а другая половина хуже. Отклонение
результатов числа отжиманий в упоре лежа
внутри группы равно 6 отжиманиям. Результаты
исследования имеют малую варьируемость, что
говорит об однородности выборки, то есть
средний результат типичен для изучаемого
признака.
n
X
x Sx
R
M0 V
me

13. Пример записи решения задания к Части II РГР №1

ПРИМЕР ЗАПИСИ РЕШЕНИЯ ЗАДАНИЯ
К ЧАСТИ II РГР №1
Задание: По данным выборки:
1. Составить интервальный вариационный ряд.
2. Построить гистограмму.
3. Найти средние характеристики:
а) среднее выборочное x ;
б) моду M 0 ;
в) медиану me .
4. Найти характеристики вариации:
а) размах вариации X R ;
б) дисперсию D;
в) среднее квадратическое отклонение ;
г) коэффициент вариации V;
д) ошибку выборочного среднего .
5. Сделать вывод.
Исходные данные:
Бег на 100 м (юноши 9 классов)
16,2
15,3
15,3
16,8
16,2
15,5
16,0
15,8
16,0
15,5
14,3
13,7
14,2
14,6
13,6
16,6
16,1
15,8
15,6
16,4
15,8
16,2
14,2
16,1
15,2
15,4
15,3
15,4
17,8
15,9
14,5
15,5
14,7
15,6
15,0
14,8
14,8
12,8
15,0
14,2
16,1
14,3
16,9
15,6
16,4
15,8
16,2
15,0
15,0
14,2

14.

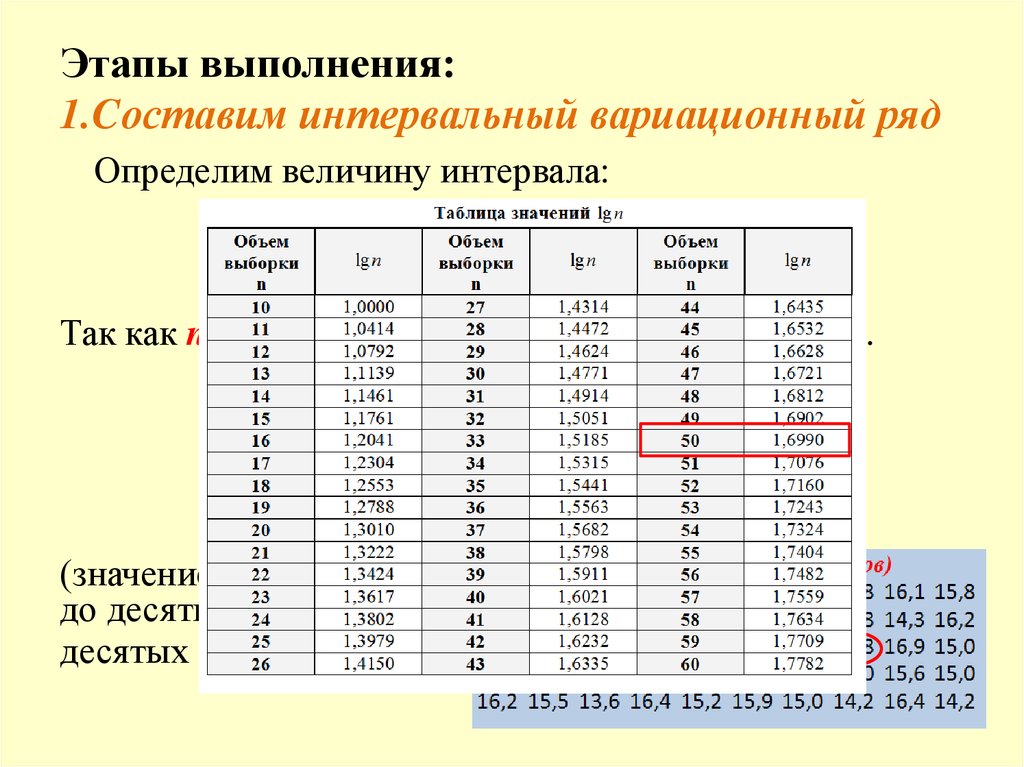
Этапы выполнения:
1.Cоставим интервальный вариационный ряд
Определим величину интервала:
xmax x
min
h
1 3,32 lg n
Так как n=50, определим значения lg50, xmax и xmin .
lg50=1,6990, xmax 17,8 , xmin 12,8
h
17,8 12,8
5
5
0,8
1 3,32 lg 50 1 3,32 1,699 6,64
(значение величины интервала округляем с точностью
до десятых, так как исходные данные имеют точность до
десятых долей).

15.

Найдем границы интервалов.
Левой границей первого интервала будет число
a1 x min
h
2
a1 12,8
0,8
12,4
2
Вычисляем далее
a 2 a1 h
a 2 12,4 0,8 13,2
a3 a 2 h
a 3 13,2 0,8 14,0
a 4 14,0 0,8 14,8
a 5 14,8 0,8 15,6
a 6 15,6 0,8 16,4
a 7 16,4 0,8 17,2
a8 17,2 0,8 18,0
xmax 17,8

16.

Результаты оформляем в таблицу:
Интервалы
Частоты
ni
12,4-13,2 13,2-14,0 14,0-14,8 14,8-15,6 15,6-16,4 16,4-17,2 17,2-18,0
1
2
9
15
17
5
1

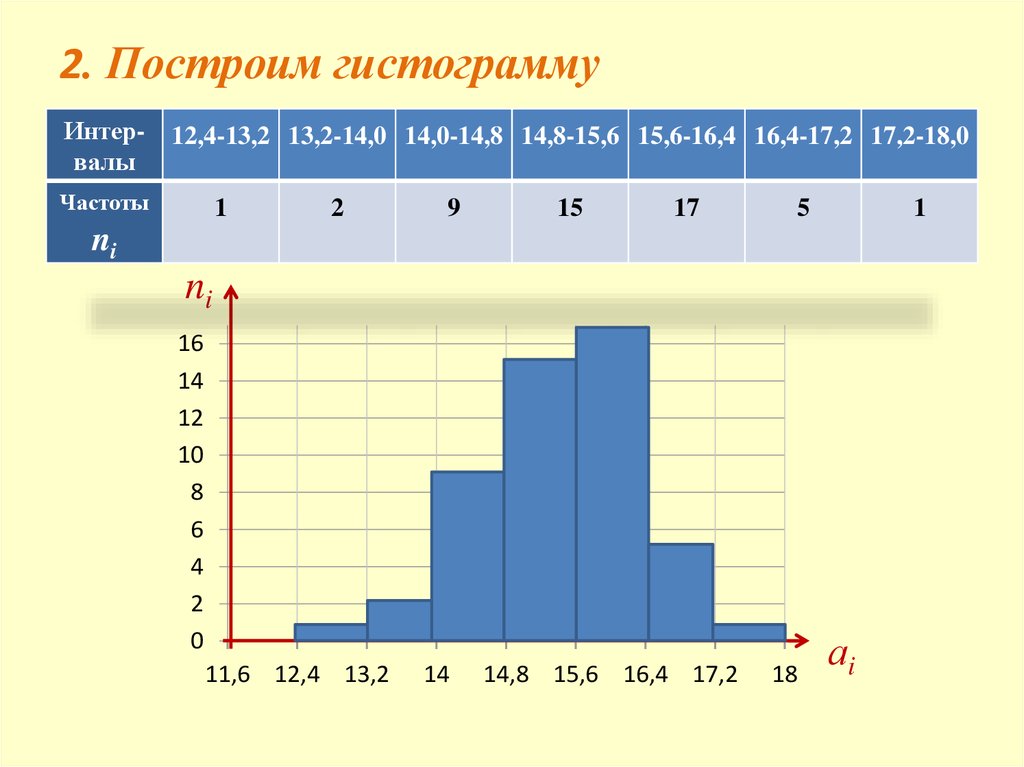
17.

2. Построим гистограмму
Интервалы
12,4-13,2 13,2-14,0 14,0-14,8 14,8-15,6 15,6-16,4 16,4-17,2 17,2-18,0
Частоты
1
2
9
15
17
5
1
ni
ni
16
14
12
10
8
6
4
2
0
11,6 12,4 13,2
14
14,8 15,6 16,4 17,2
18
аi

18.

Интер12,4-13,2средние
13,2-14,0характеристики
14,0-14,8 14,8-15,6 15,6-16,4
3.
Вычислим
валы
а)
Определим среднее выборочное :
1
Частоты
1
2
9
15
ni
Вычисления оформим в виде таблицы:
x17
16,4-17,2 17,2-18,0
n
x5 n
n
i 1
xi
ni
xi ni
12,8
13,6
14,4
15,2
16,0
16,8
18,4
1
2
9
15
17
5
1
12,8
27,2
129,6
228
272
84
18,4
=772
1
x 772 15,4
50
i i
1

19.

б) Определим моду:
Интервалы
Частоты
12,4-13,2 13,2-14,0 14,0-14,8 14,8-15,6 15,6-16,4 16,4-17,2 17,2-18,0
1
2
9
15
17
5
ni
M 0 a1M 0 h
nM 0 nM 0 1
2nM 0 nM 0 1 nM 0 1
17 15
M 0 15,6 0,8
15,7
2 17 15 5
1

20.

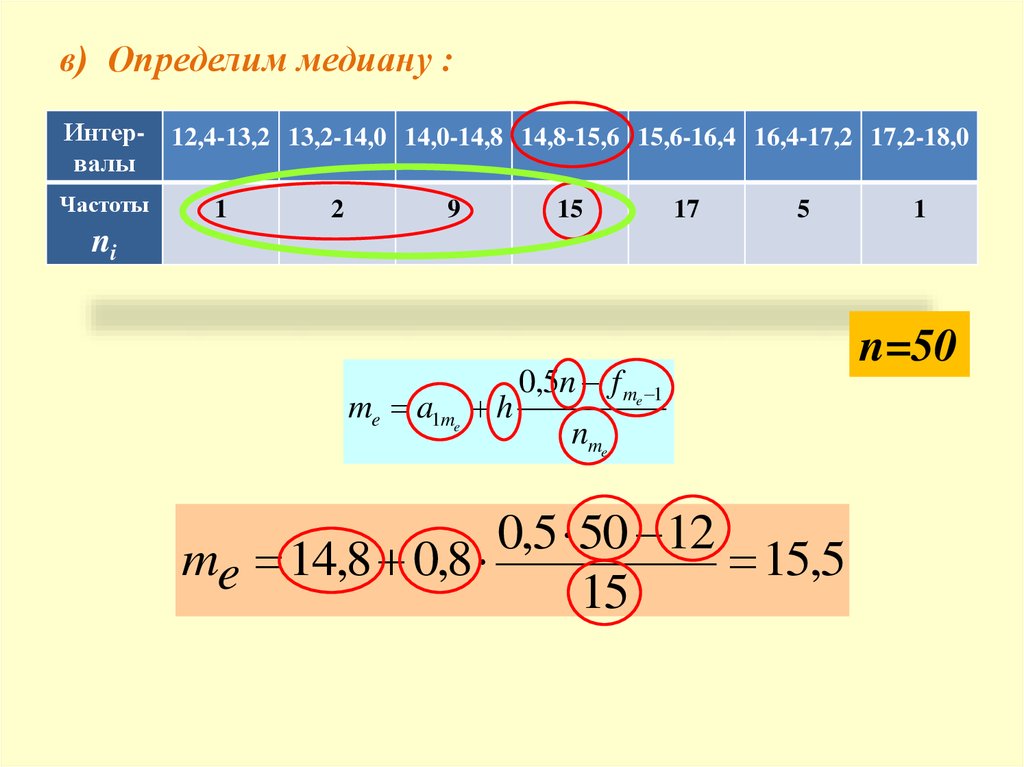
в) Определим медиану :
Интервалы
Частоты
12,4-13,2 13,2-14,0 14,0-14,8 14,8-15,6 15,6-16,4 16,4-17,2 17,2-18,0
1
2
9
15
17
5
1
ni
me a1me h
0,5n f me 1
nme
0,5 50 12
me 14,8 0,8
15,5
15
n=50

21.

4. Вычислим характеристики вариации
а) Определим размах вариации :
X R xmax x
min
xmin 12,8
xmax 17,8
X R 17,8 12,8 5,0

22.

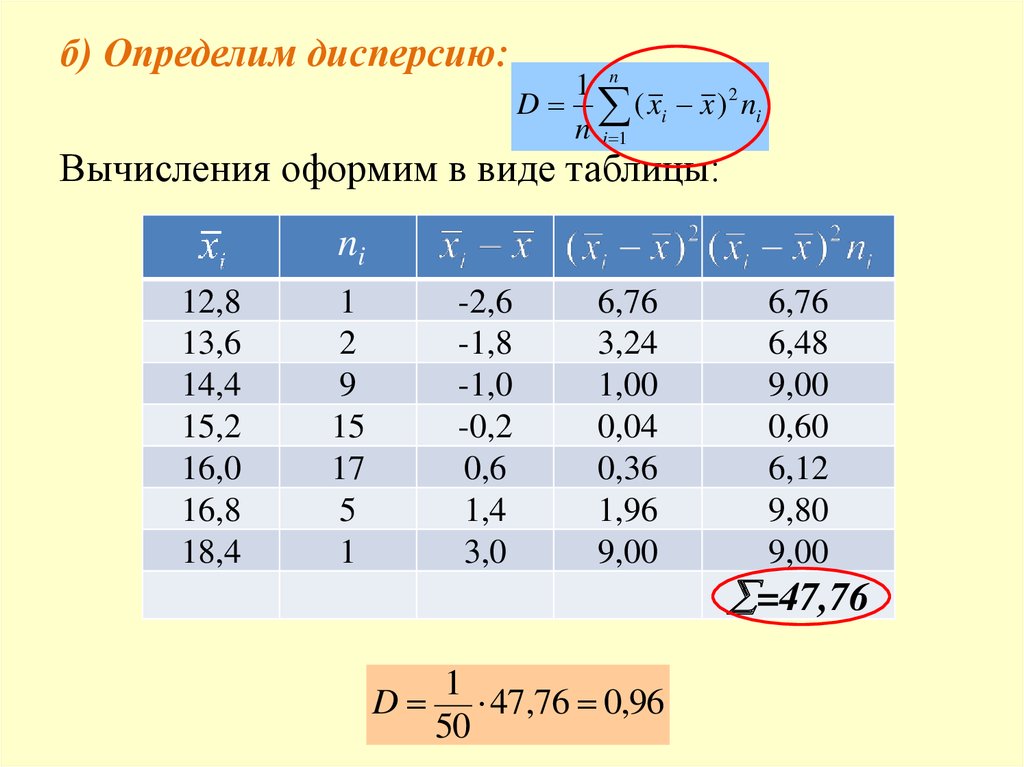
б) Определим дисперсию:
1 n
D ( xi x ) 2 ni
n i 1
Вычисления оформим в виде таблицы:
ni
12,8
13,6
14,4
15,2
16,0
16,8
18,4
1
2
9
15
17
5
1
-2,6
-1,8
-1,0
-0,2
0,6
1,4
3,0
6,76
3,24
1,00
0,04
0,36
1,96
9,00
1
D 47,76 0,96
50
6,76
6,48
9,00
0,60
6,12
9,80
9,00
=47,76

23.

в) Определим среднее квадратическое отклонение:
D
0,96 0,98 1,0

24.

г) Определим коэффициент вариации:
V
x
100%
0,98
V
100% 0,064 100% 6,4%
15,4

25.

д) Определим ошибку выборочного среднего:
Sx
n
0,98
Sx
0,1
50

26.

5. Вывод. По данным результатов в беге на 100 м 50
испытуемых средний результат составил 15,4 с ± 0,1 с.
Степень рассеяния данных выборки от среднего
результата составляет 1с. Чаще всего встречаемый
результат в группе – 15,7с. Одна половина бегунов
показала результаты лучше 15,5с, а другая половина
хуже. Отклонение результатов в беге на 100 м внутри
группы составляют 5с. Результаты исследования
имеют малую варьируемость, что говорит об
однородности выборки, то есть средний результат
типичен для изучаемого признака.
x Sx n
XR
M0 V
me