Элементы математической статистики. Практическое занятие 15

1.

Практическое занятие 15
Элементы математической статистики
Вопросы
1.Основные задачи математической статистики.
2.Понятие о выборочном методе исследования.
3.Основные задачи выборочного метода.
4. Определение вариационного ряда.
5. Статистическое распределение выборки.
6. Таблица частот выборки.
7. Эмпирическая функция распределения.
8.Полигон частот.
9. Гистограмма частот и ее построение.
10.Точечная оценка параметра.
11. Методы получения точечных оценок.
12. Доверительный интервал для математического ожидания нормального распределения
при известной дисперсии.
13. Доверительный интервал для дисперсии нормального распределения. Доверительный
интервал для дисперсии нормального распределения.
I. Выборочный метод исследования
Вариационным рядом выборки называется способ её записи, при котором элементы упорядочиваются по величине, т.е. записываются в виде: x (1) , x ( 2) ,..., x n , где x (1) x ( 2 ) ... x n .
Статистическим рядом называется последовательность пар ( xi , k i ).
Пример 1. Дана выборка 3,8,1,3,6,5,2,2,7. Записать в виде вариационного ряда и статистического распределения.
Решение. Используя определение вариационного ряда, записываем 1,2,2,3,3,5,6,7,8.
Статистическое распределение, учитывая объем n=9, будет вида:
Х
1
2
3
5
6
7
8
n
1
2
2
1
1
1
1
Или с относительными частотами:
Х
1
2
3
5
6
7
8
ni / n
1/9
2/9
2/9
1/9
1/9
1/9
1/9
Контроль:
ni
1.
n
Пример 2. Представить выборку 55 наблюдений в вмде таблицы частот, используя 7 интервалов группировки. Выборка:
17
19
23
18
21
15
16
13
20
18
15
20
14
20
16
14
20
19
15
19
16
19
15
22
21
12
10
21
18
14
14
17
16
13
19
18
20
24
16
20
19
17
18
18
21
17
19
17
13
17
11
18
19
19
17
Решение. Разность между наибольшим и наименьшим элементом равна 24-10=14, тогда шаг
интервала будет 14/ 7=2, объем выборки 55. Составим таблицу:

2.

Номер интервала
границы
частота
Относительная
1
10 - 12
2
0,0364
2
12 - 14
4
0,0727
3
14 - 16
8
0,1455
4
16 - 18
12
0,2182
5
18 – 20
16
0,2909
6
20 – 22
10
0,1818
7
22 - 24
3
0,0545
Σ=55
Σ=1
II. Эмпирическая функция распределения. Функция F x
частота
n x
называется функцией
n
распределения выборки случайной величины .
Пример 4. В результате выборки имеем -3,+2,-1,-3,+5,-3,+2. Построить график эмпирической функции распределения.
Решение. n 7, x1 x 4 x 6 3;
0,
3,
n x 4,
6,
7,
x 2 x7 2 .
0,
3
x 3
,
7
3 x 1
n x 4
1 x 2 F x
,
n
7
2 x 5
6
x 5
7 ,
1,
x 3
3 x 1
1 x 2
2 x 5
x 5.
На примере видны основные особенности эмпирической функции распределения. Как
и теоретическая, она не убывает, и ее значения 0,1 . Но эта формула всегда ступенчатая.
Эмпирическая функция не зависит от того, в каком порядке сделана выборка, т.е. от того, в
каком порядке идут числа в последовательности: x1 x 2 ...x n (рис.1).
Рисунок 1

3.

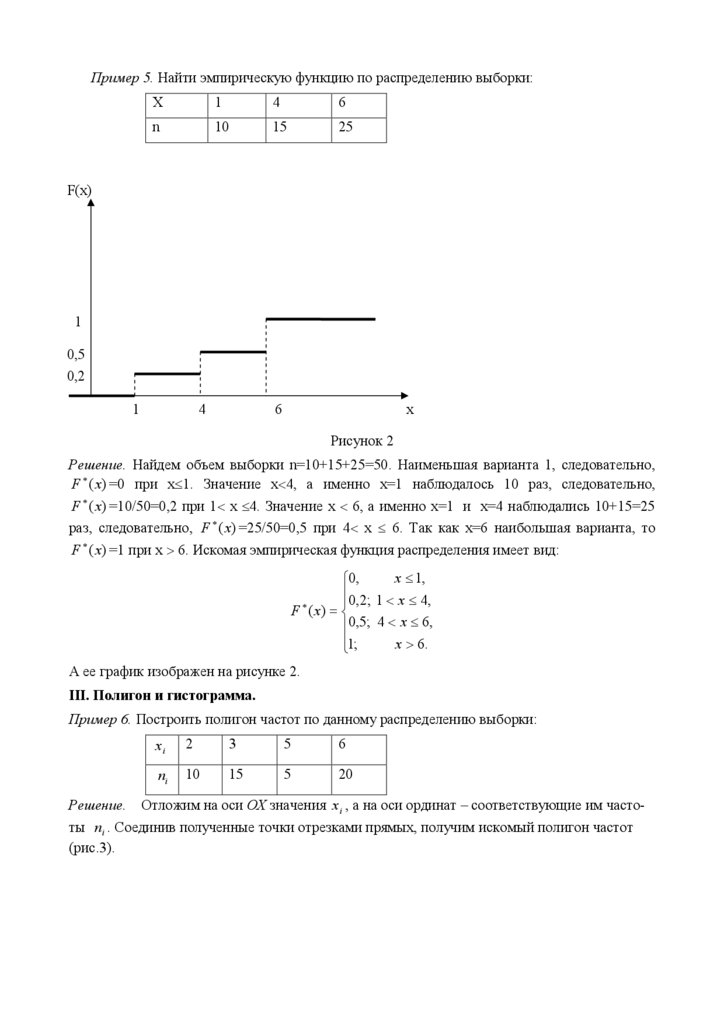
Пример 5. Найти эмпирическую функцию по распределению выборки:
Х
1
4
6
n
10
15
25
F(х)
1
0,5
0,2
1
4
6
х
Рисунок 2
Решение. Найдем объем выборки n=10+15+25=50. Наименьшая варианта 1, следовательно,
F (x) =0 при х 1. Значение х 4, а именно х=1 наблюдалось 10 раз, следовательно,
F (x) =10/50=0,2 при 1 х 4. Значение х 6, а именно х=1 и х=4 наблюдались 10+15=25
раз, следовательно, F (x) =25/50=0,5 при 4 х 6. Так как х=6 наибольшая варианта, то
F (x) =1 при х 6. Искомая эмпирическая функция распределения имеет вид:
x 1,
0,
0, 2; 1 x 4,
F ( x)
0,5; 4 x 6,
1;
x 6.
А ее график изображен на рисунке 2.
III. Полигон и гистограмма.
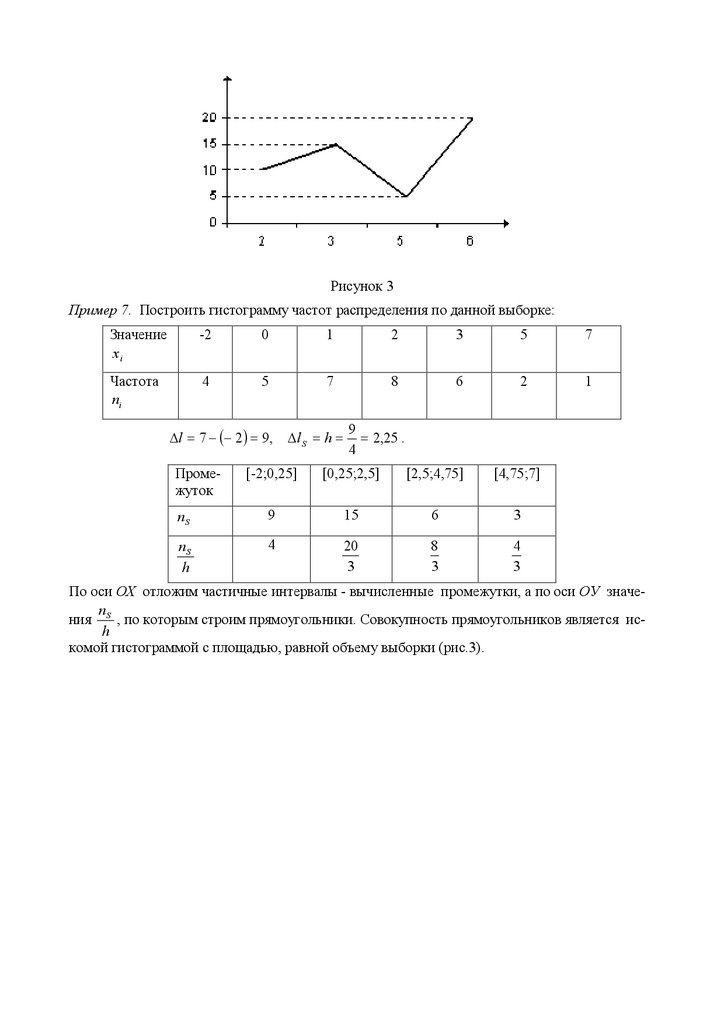
Пример 6. Построить полигон частот по данному распределению выборки:
xi
2
3
5
6
ni
10
15
5
20
Решение. Отложим на оси ОХ значения x i , а на оси ординат – соответствующие им частоты ni . Соединив полученные точки отрезками прямых, получим искомый полигон частот
(рис.3).

4.

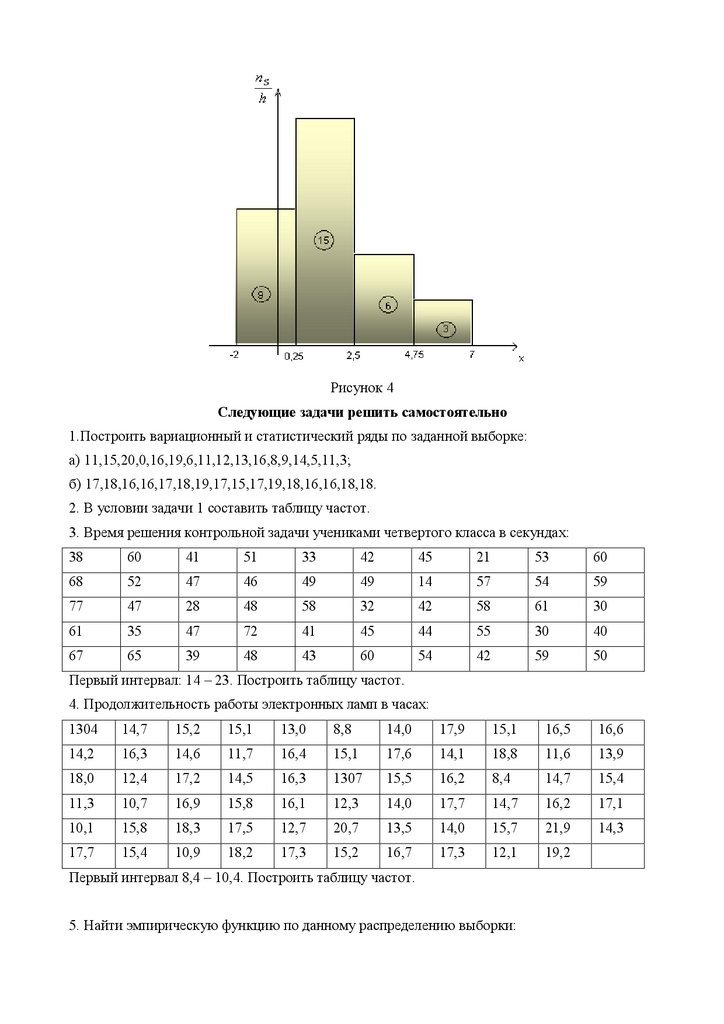
Рисунок 3
Пример 7. Построить гистограмму частот распределения по данной выборке:
Значение
xi
-2
0
1
2
3
5
7
Частота
ni
4
5
7
8
6
2
1
l 7 2 9,
l S h
9
2,25 .
4
Промежуток
[-2;0,25]
[0,25;2,5]
[2,5;4,75]
[4,75;7]
nS
9
15
6
3
nS
h
4
20
3
8
3
4
3
По оси ОХ отложим частичные интервалы - вычисленные промежутки, а по оси ОУ значеn
ния S , по которым строим прямоугольники. Совокупность прямоугольников является исh
комой гистограммой с площадью, равной объему выборки (рис.3).

5.

Рисунок 4
Следующие задачи решить самостоятельно
1.Построить вариационный и статистический ряды по заданной выборке:
а) 11,15,20,0,16,19,6,11,12,13,16,8,9,14,5,11,3;
б) 17,18,16,16,17,18,19,17,15,17,19,18,16,16,18,18.
2. В условии задачи 1 составить таблицу частот.
3. Время решения контрольной задачи учениками четвертого класса в секундах:
38
60
41
51
33
42
45
21
53
60
68
52
47
46
49
49
14
57
54
59
77
47
28
48
58
32
42
58
61
30
61
35
47
72
41
45
44
55
30
40
67
65
39
48
43
60
54
42
59
50
Первый интервал: 14 – 23. Построить таблицу частот.
4. Продолжительность работы электронных ламп в часах:
1304
14,7
15,2
15,1
13,0
8,8
14,0
17,9
15,1
16,5
16,6
14,2
16,3
14,6
11,7
16,4
15,1
17,6
14,1
18,8
11,6
13,9
18,0
12,4
17,2
14,5
16,3
1307
15,5
16,2
8,4
14,7
15,4
11,3
10,7
16,9
15,8
16,1
12,3
14,0
17,7
14,7
16,2
17,1
10,1
15,8
18,3
17,5
12,7
20,7
13,5
14,0
15,7
21,9
14,3
17,7
15,4
10,9
18,2
17,3
15,2
16,7
17,3
12,1
19,2
Первый интервал 8,4 – 10,4. Построить таблицу частот.
5. Найти эмпирическую функцию по данному распределению выборки:

6.

а)
xi
2
5
7
8
ni
1
3
2
4
xi
4
7
8
9
ni
5
2
3
4
б)
6. Построить полигон частот по данному распределению выборки:
xi
15
20
25
30
10
ni
10
15
30
20
25
7. Изменение емкости затвор-сток у 80 полевых транзисторов дали следующие результаты:
1,9
3,1
1,3
0,7
3,2
1,1
2,9
2,7
2,7
4,0
1,7
3,8
0,9
0,8
3,1
1,2
2,6
1,9
2,3
3,2
4,1
1,3
2,4
4,5
2,5
0,9
1,4
1,6
2,2
3,1
1,5
1,1
2,3
4,3
2,1
0,7
1,2
1,5
1,8
2,9
0,8
0,9
1,7
4,1
4,3
2,6
0,9
0,8
1,2
2,1
3,2
2,9
1,1
3,2
4,5
2,1
3,1
5,1
1,1
1,9
0,9
3,1
0,9
3,1
3,3
2,8
2,5
4,0
4,3
1,1
2,1
3,8
4,6
3,8
2,3
3,9
2,4
4,1
4,2
0,9
Построить гистограмму частот по этой выборке, предварительно составив соответствующую
таблицу группировки. В качестве длины интервала взять следующие значения:
а) h=0,3; б) h=0,6; в) h=1,2.
8. Построить гистограмму частот по данному распределению выборки:
Номер интервала
Частичный
интервал
Сумма частот
вариант
1
2–7
5
2
7 – 12
10
3
12 – 17
25
4
17 – 22
6
5
22 - 27
4
Плотность частоты
9. Построить гистограмму частот по данному распределению выборки:
Номер интервала
Частичный
интервал
Сумма частот
вариант
1
3–5
4
2
5–7
6
Плотность частоты

7.

3
7–9
20
4
9 – 11
40
5
11 – 13
20
6
13 – 15
4
7
15 - 17
6
IV. Точечные оценки.
Пример 1. Контрольные обмеры диаметров болтов дали следующие результаты: 2,31; 2,28;
2,29; 2,28; 2,32; 2,28; 2,32; 2,29; 2,31; 2,32.
Найти точечные оценки для диаметра болта и его дисперсии в контролируемом процессе
производства.
x
x1 ... x n
2,3;
10
S2
1 n
2
M x k x 0,0003 .
n 1 k 1
Пример2.
Известно, что случайная величина имеет распределение Пуассона
a m a
P m
e ,
m!
неизвестным является параметр a . Используя указанные выше методы получения точечных
*
оценок, найти по выборке x 1 , x 2 , , x n значение a неизвестного параметра a .
Решение.
Решим задачу двумя методами.
1 Метод моментов
В формуле М х подсчитаем М и х , используя заданную выборку:
14, 12, 9, 8, 15, 7, 11, 8 , n 30 .
a 14 a
a 12 a
a9
a8
e 12
e 9 e a 8 e a
i 1
14!
12!
9!
8!
15
7
11
8
a
a
a
a
15
e a 7 e a 11
e a 8 e a
15!
7!
11!
8!
a 13 a 11 a 8 a 7 a 14 a 6 a 10 a 7
e a a
13
!
11
!
8
!
7
!
14
!
6
!
10
!
7!
a2 a3 a4
an
a
e 1 a
e a ae a a.
2! 3! 4!
n!
1 8
1
21
x x i 14 12 9 8 15 7 1 8
10,5 .
8 1
8
2
*
Из равенства М x получаем a 10,5 , т.е. a 10,5 .
М x i p i 14
2 Метод максимального подобия
Составим функцию правдоподобия:

8.

2
a 14 a a 12 a a 9 a a 8 a a15 a a 7 a a 11
L x1 , x 2 , , x n , а
e
e e e
e e
14!
12!
9!
7!
11!
8!
15!
1
е 8 а .a 14 12 9 16 15 7 11 A e 8a a 84 L(a).
2
14! 12! 9! 8! 15! 7! 11!
Исследуем функцию одной переменой L(a ) на экстремум.
Необходимым условием экстремума является L (a) =0 или
A e 8a 8 a 84 e 8a 84a 83 Ae 8a a 83 8a 84 0 .
8а 84 0 , а 21 / 2 10,5 . Следовательно, а 10,5 - критическая точка.
Достаточным условием экстремума является знак второй производной в критической
точке:
L (a ) A e 84 8 a 83 8a 84 e 8a 83a 82 8a 84 e 84 8 a 83
Ae 8a 8a 82 a 8a 84 83 a 10,5
8Ae 8 a a 82 8a 2 84a 83a 83 10,5 a 8Ae 8 a a 82 8a 2 18a 871,5 .
L 10,5 8Ae 8 a a 82 8 10,5 2 18 10,5 871,5 8Ae 8 a a 82 882 1764 871,5
83
8Ae 8 a 10,5 1 0 .
Следовательно, значение a 10,5 является максимальным значением функции L(a ) ,
отсюда понятно название метода максимального правдоподобия.
*
Ответ: a 10,5 .
Пример 3.
Известно, что случайная величина имеет биноминальное распределение
р ( m) C mn p m (1 p) n m ,
неизвестным является параметр p . Используя методы получения точечных оценок, найти по
*
реализации выборки x 1 , x 2 , , x n значение p неизвестного параметра p .
Решение.
Пусть выборка будет, что и в предыдущей задаче. Решим поставленную задачу двумя
способами.
1 Метод моментов
В формуле М х вычислим правую и левую части, используя условие задачи: выборка 14, 12, 9, 8, 15, 7, 11, 8 , n 30 .
1 8
x x i 10,5 .
8 1
М x i p i 14 С 1430 p 14 1 p 12 С 1230 p 12 1 p 9 С 930 p 9 1 p
16
18
21
i 1
2 8 С 830 p 8 1 p 15 С 1530 p 15 1 p 11 С 1130 p 11 1 p
30! 14
30! 12
30! 11
16
18
19
14
p 1 p 12
p 1 p 9
p 1 p 30р.
14! 16!
12! 18!
9! 21!
29! 7
29! 14
29! 6
29! 10
22
15
23
19
p 1 p
p 1 p
p 1 p
p 1 p
2
14! 15!
6! 23!
10! 19!
7! 22!
22
15
19

9.

30р С 1329 p 13 1 p С 1129 p 11 1 p С 729 p 7 1 p
15
18
21
С 729 p 7 1 p С 1429 p 14 1 p С 1129 p 11 1 p С 729 p 7 1 p
22
15
18
22
2 С 729 p 7 1 p С 1429 p 14 1 p С 629 p 6 1 p С 1029 p 10 1 p
22
p q
29
15
23
19
p 29 С 2829 p 28 1 p С 2729 p 27 1 p С 2629 p 26 1 p
2
С 129 p 1 p 1 p
28
3
29
30 p p 1 p 30 p.
29
*
Подставляя в формулу М х , получим 30 p 10,5 , p 0,35 .
V. Доверительные интервалы
Пример 4. Случайная величина распределена по нормальному закону с параметром 2 .
Сделана выборка n 25 . Найдем с надежностью 0,95 доверительный интервал для неизвестного параметра a этого распределения.
1
Из равенства t или t 0,475 по таблице t 1,96 . Тогда точность оценки есть
2
2
t
1,96 0,784 .
n
25
Тогда x 0,784 a x 0,784 .
Если для сделанной выборки x 2,3 , то с надежностью 0,95 интервал (1,5; 3,1) покрывает
параметр a с точностью до 0,8 и надежностью 95 %.
Пример 5. Вычислить с надежностью 0,96 доверительный интервал для D нормальное
распределение по выборке n 18 .
Решение.
Предварительно рассмотрим таблицу 3 в приложении, с помощью которой решается
поставленная задача. Для определения 1 используем входные данные
1
1
n 1,
и для 2 - n 1,
. По условию задачи =17 и α=0,98, то2
2
гда 1 =7,26, а для определения 2 имеем =19 и α=0,02, тогда 2 =33,7.
17 S 2 17 S 2
Следовательно, искомый доверительный интервал будет
,
33.7 7.26
Следующие задания решить самостоятельно
Найти точечные оценки по выборке x 1 , x 2 , , x n объема n для параметров указанных распределений при помощи двух методов:
1. Пуассоновское распределение с параметром :
a k
P k
e .
k!
x
2. Показательное распределение f ( x ) e , x 0 и f ( x ) 0 при x 0 .
3. Нормальное распределение f ( x )
1
2
e
x m 2
2 2
для всех x .

10.

4. Случайная величина ξ имеет нормальное распределение с неизвестными математическим ожиданием а и дисперсией σ. По выборке объема n=26 вычислены
a 1,7; ( 2 ) 0,8; 0,9. Найти доверительный интервал для математического ожидания
а, отвечающий доверительной вероятности .
5. В результате n=46 опытов получена несмещенная оценка ( 2 ) 64 для дисперсии
нормальной случайной величины. Найти доверительный интервал для дисперсии при доверительной вероятности =0,98.
6. В серии из n=41 выстрелов по мишени наблюдалось m=24 попаданий в цель. Найти
доверительный интервал для вероятности p попаданий в мишень при доверительной вероятности =0,95 и u =1,96 – значение аргумента функции Лапласа, при котором Ф( u )= /2.
7. В серии из n опытов событие не наступило ни разу. Определить число опытов n,
при котором верхняя доверительная граница для вероятности Р(А) числу 0,032 при =0,95.
Литература
1.Гнеденко Б.В. Курс теории вероятности. М.: Высшая школа, 1969г.
2.Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1998г.
3. Чистяков В.П. Курс теории вероятностей. М.: Высшая школа, 1982г.
4. Вентцель Е.С., Овчаров Л.А. Теория вероятностей (задачи и упражнения). М.: Высшая школа,
1973г.
5. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистики. М.: Высшая школа, 1998г.
6. Чудесенко В.Ф. Сборник заданий по специальным курсам высшей математики (типовые расчета).
М.: Высшая школа, 1983 г.