Похожие презентации:
Коло і круг
1.
Коло і круг2.
3.
ПРОБЛЕМА!!!Де круг?
Де коло?
О
4.
Циркуль – це креслярськийінструмент. З ним потрібно
працювати обережно. На одному
кінці у нього — голка, на іншому —
олівець.
5.
Позначтет.О
Завдання
№1:
1.
О
2. Розхил циркуля
дорівнює 3 см.
3. Поставте вістря
циркуля в точку О
і проведіть
замкнену лінію.
6.
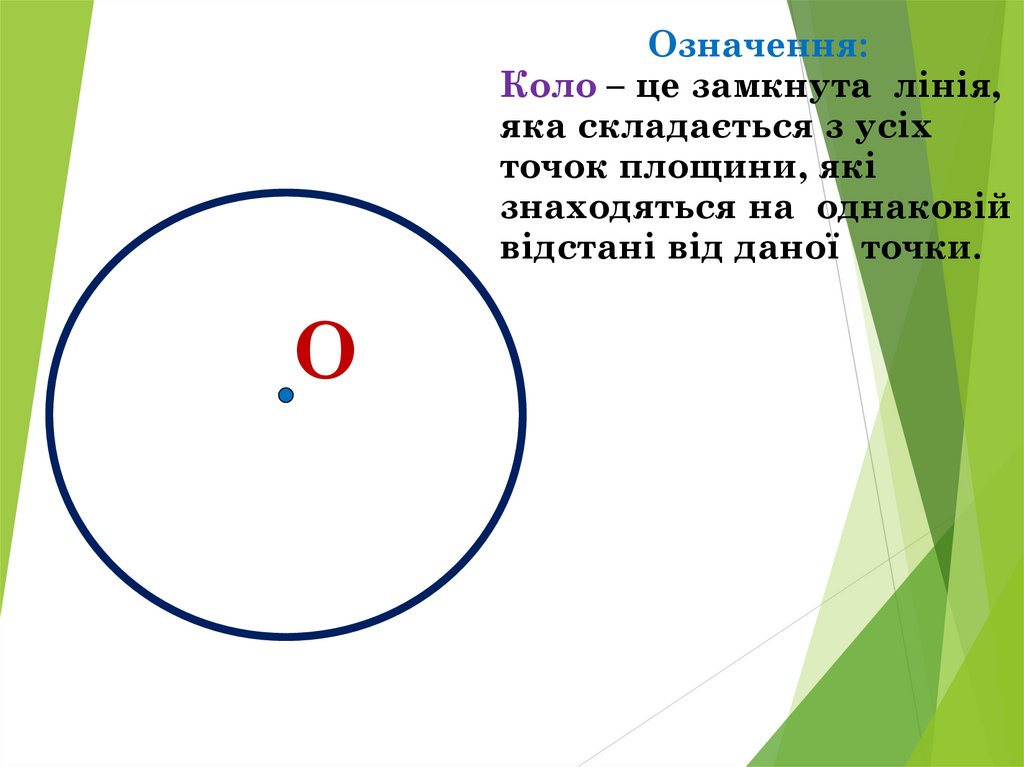
Означення:Коло – це замкнута лінія,
яка складається з усіх
точок площини, які
знаходяться на однаковій
відстані від даної точки.
О
7.
Мт. О – центр кола
Позначемо на
колі дві точки А і
М.
О
З’єднаємо точки
О і М, О і А.
Відрізки ОА і ОМ
– радіуси кола.
А
Означення:
Відрізок, який з’єднує центр кола з точкою на колі,
називають радіусом.
8.
МСкільки радіусів у
кола?
Що можна сказати
про них?
О
А
ОА=ОМ=R
9.
Завдання№2: М
Продовжіть відрізок
АО до перетину з
колом.
К
Позначте точку
перетину буквой
К.
О
А
Відрізок АК –
називається
діаметром кола.
Означення:
Діаметр – це відрізок, який з’єднує дві точки на колі і
проходить через його центр.
10.
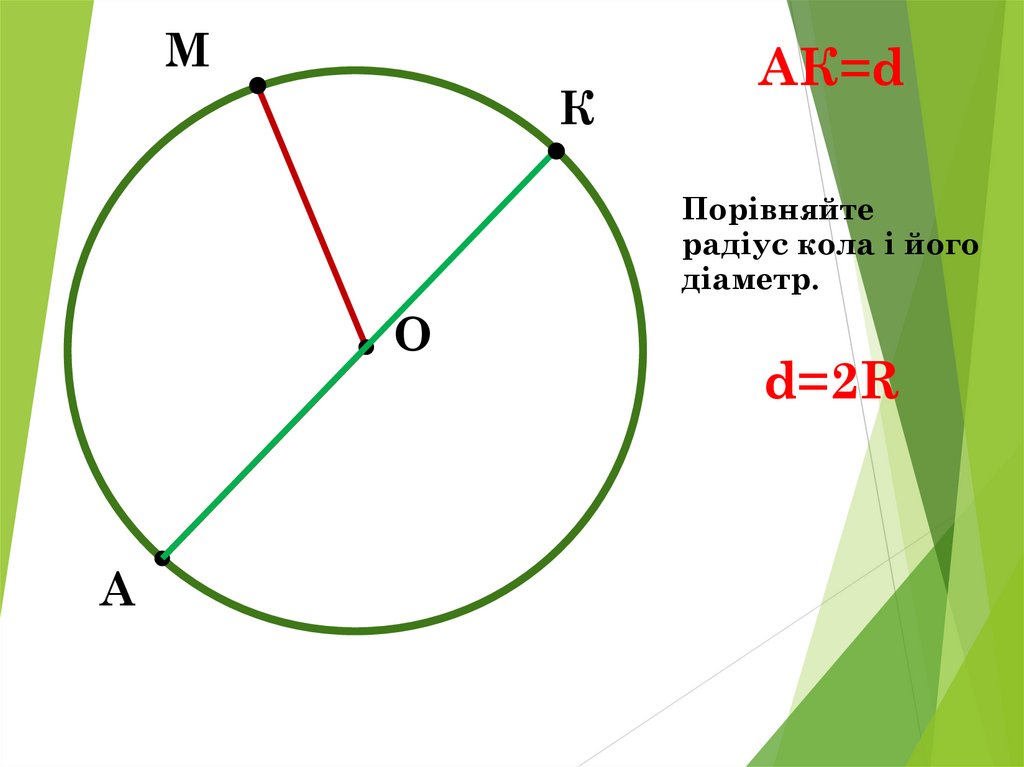
МК
АК=d
Порівняйте
радіус кола і його
діаметр.
О
А
d=2R
11.
МК
З’єднайте точки
М і К, А і М.
Відрізки МК та
АМ називаються
хордами кола.
О
Як по іншому
назвати діаметр?
А
Означення:
Хорда – це відрізок, який з’єднує дві точки на колі.
12.
СНазвіть усі радіуси ,
діаметри і хорди кола.
В
D
O
А
L
E
F
K
13.
РПобудуйте коло з
центром в точці О
довільного радіуса.
Позначте дві точки А і
В.
О
А
Н
В
ВНА, ВРА – дуги кола.
Точки А і В поділили
коло на дві частини,
які називаються
дугами кола.
14.
Т е о р е м а 1 (про порівняння діаметра і хорди).Діаметр є найбільшою з хорд.
Д о в е д е н н я. Нехай AB — довільний діаметр
кола, радіус якого дорівнює r, а MN — хорда кола,
відмінна від діаметра (мал. 2). Доведемо, що AB >
MN. AB = 2r. У трикутнику MON, використовуючи
нерівністьтрикутника, маємо MN < MO + ON. Отже,
MN < 2r. Тому AB > MN. Теорему доведено.
Рис. 2
15.
•Об'єднання кола зйого внутрішньою
частиною
О



















 Математика
Математика








