Похожие презентации:
Оптимизация производства
1. 3. Оптимизация производства
2.
3.1 Аналитическое решениеоптимизации производства
задачи
3. Оптимизация производства при отсутствии ограничений
4.
Рассмотрим аналитическое решение задачи оптимизациипроизводства, полагая, что производственный процесс
характеризуется нелинейной производственной функцией
Y(K, L), которая описывает зависимость объема выпуска Y от
двух переменных - объема вложенного капитала (K) и
вложенного труда (L).
Это может быть, например, неоклассическая производственная
функция вида
Y(K, L)=AK L
(мультипликативная функция).
Задача лица, принимающего решения, состоит в том, чтобы
определить значения K и L, максимизирующие прибыль
производителя.
5.
6.
7.
8.
Чтобы определить, при каких условиях прибыль П являетсямаксимальной, найдем экстремум этой функции. Необходимое
условие экстремума:
pдY/дK = r
pдY/дL = w
Данное выражение определяет оптимальное решение задачи
производителя. Поскольку в левых частях уравнений стоят
предельная фондоотдача и предельная производительность,
экономически полученный результат можно интерпретировать
так: производитель достигает максимальной прибыли, когда
значение предельного продукта (увеличения выпуска при
увеличении фактора производства на единицу) равно цене на
ресурс.
9.
Пример. Пусть некая фирма имеет производственнуюфункцию
R(K, L) =pY(K, L)=100K1/2L1/3.
Средняя заработная плата составляет w = 103 ден. ед. в мес. и
период амортизации основных производственных фондов
n = 12 мес. Требуется рассчитать оптимальный размер
производственных фондов и оптимальную численность
работников. Затем нужно определить, сколько составит
прибыль фирмы при переходе к оптимальным затратам
факторов производства
10.
Решение. Цена труда известна, а цена капитала равна 1/12ден.ед. в месяц – среднемесячные амортизационные
отчисления на содержание одной единицы капитала.
Продифференцировав Y по капиталу и труду, получаем
систему уравнений
50K-1/2L1/3 = 1/12
100/3K1/2L-2/3 = 103,
откуда K=144 000 000, L=8000, Y= 24 000 000, П=4 млн. ден.ед.
11.
Если на поведение производителя влияют некиедополнительные внешние факторы, рассмотренную
модель всегда можно усложнить, включив в нее описание
этого влияния. В качестве примера рассмотрим, как влияет
на
поведение
производителя
государственное
налогообложение.
Пример. Ответьте, что сильнее влияет на поведение
производителя – налог на прибыль или акцизный налог?
Оба налога характеризуются ставкой t, для которой
выполняется условие 0 < t < 1.
12.
Решение. Рассмотрим для начала налог на прибыль. Для егорасчета прибыли необходимо использовать выражение
П1= (1-t) П
Условие максимума для П1 совпадает с условием для П, а значит
оптимальные значения K, L и Y останутся прежними.
При введении акцизного налога
П1= (1– t)R–C=(1– t)pY(K, L) –rK–wL.
Условия экстремума:
(1– t)дY/дK = r
(1– t)дY/дL = w
С учетом того, что у большинства производственных функций
первые производные являются положительными убывающими
функциями (увеличиваются при уменьшении значения
аргумента), можно утверждать, что положение экстремума для
прибыли окажется смещенным в сторону меньших затрат труда
и капитала.
13. Оптимизация производства при наличии бюджетного ограничения (метод Лагранжа)
14.
Производитель может столкнуться с ситуацией, когдаобеспечить набор факторов производства, соответствующий
точке максимума П невозможно, например, в силу того, что
ресурсы, доступные для использования в производственном
процессе, ограничены, либо в силу особенностей самого
производственного процесса (в силу вида производственной
функции). В этом случае необходимо осуществить поиск
оптимального решения задачи производителя при наличии
ограничений.
Возможны две постановки задачи оптимизации
производственного процесса с ограничениями:
1)
максимизация выпуска продукции при заданном уровне
затрат;
2)
минимизация затрат производства при заданном уровне
выпуска продукции.
15.
Обе эти задачи относятся к классу оптимизационных задачнелинейного программирования. Ограничения по уровню затрат
(или по объему выпуска) определяют область допустимых
планов W на которой оптимизируется выбранная целевая
функция (выпуск или затраты).
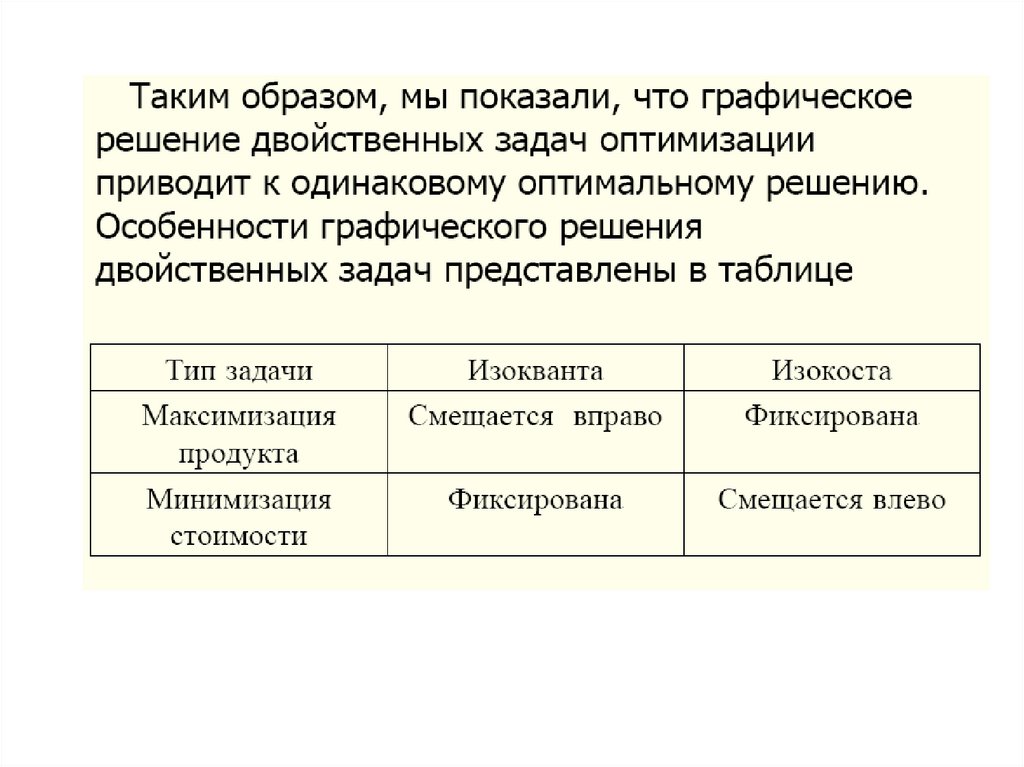
Указанные задачи оптимизации называются двойственными,
так как при одинаковых условиях дают одно и то же
оптимальное решение.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39. Влияние изменения цены на оптимальный объем производства
40.
Рассмотрим вопрос о том, как меняется оптимальное решение приизменении цены. Для этого решим несколько задач, приведенных
ниже.
1. Ответим на вопрос о том, как изменится оптимальный объем
производства при повышении цены в условиях, когда
производственная функция является неоклассической, а издержки –
линейны по капиталу и труду.
Если задача оптимизации прибыли рассматривается при отсутствии
бюджетного ограничения, для производственной функции:
П(K, L) =pY(K, L) – (rK +wL)
необходимо решить систему уравнений: pдY/дK = r
pдY/дL = w
Рост цены p при неизменных r и w означает уменьшение величины
частных производных, что для неоклассической функции будет
происходить при росте K и L, а значит Y вырастет.
41.
Если задача оптимизации прибыли решается при бюджетномограничении, т.е. имеет вид:
повышение цены не приводит к изменению оптимального объема
производства и оптимальных значений K и L. Вместе с тем,
повышение
цены
увеличивает
прибыль,
что
делает
соответствующий вид производства более привлекательным для
новых производителей.
42.
3.2 Общая постановка задачоптимизации и методы их
решения.
43.
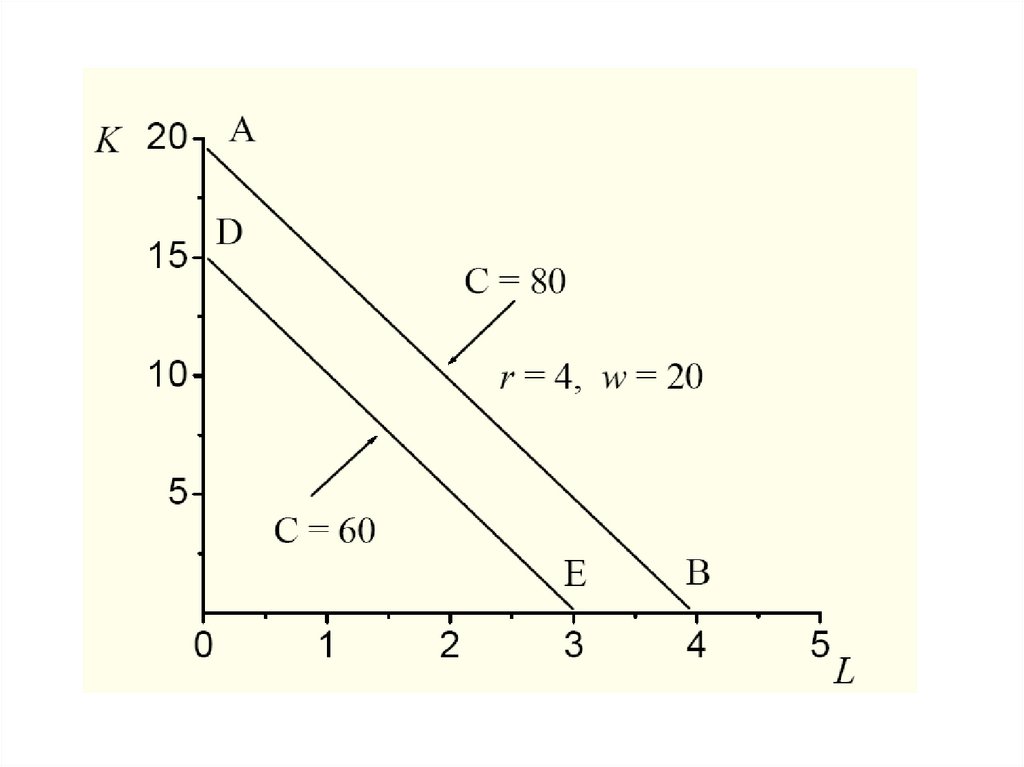
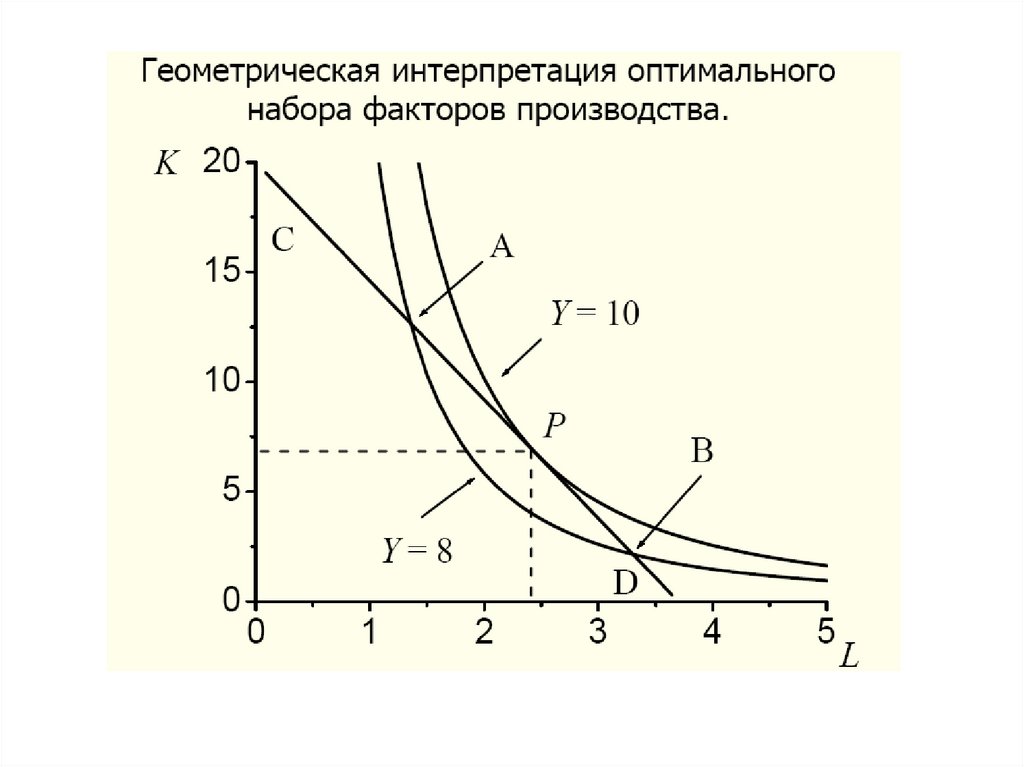
44. Для модели оптимизации, представленной ниже, областью допустимых решений W будет множество точек (K, L), лежащих на изокванте
C=rK+wL, а целевая функция – это Y(K, L)45.
46.
47.
48.
Аналитический метод решения задачоптимизации (метод Лагранжа).
49.
Пусть необходимо найти экстремум целевой функцииf(x) (здесь x =(x1, x2, x3…) – переменные задачи), при наличии
ограничений, заданных с помощью функций f1, f2, f3…
f(x) max
f1(x)=0
f2(x)=0
f3(x)=0
….
В математике подобная задача называется задачей поиска
условного экстремума. Для ее решении по методу Лагранжа
необходимо найти экстремум функции Лагранжа, которая
строится из имеющихся функций и неизвестных заранее
множителей Лагранжа 1, 2, 3 ,… в виде:
L(x)=f(x)+ 1 f1(x)+ 2 f2(x)+ 3 f3(x)+…
50.
Для поиска критической точки функции многихпеременных (функция Лагранжа зависит от исходных
переменных и всех включенных в нее множителей Лагранжа)
необходимо найти ее частные производные по всем
переменным и приравнять их к нулю.
Дальнейший анализ, необходимый для того, чтобы определить,
является ли найденная точка экстремумом, проводится на
основе значений, принимаемых в этой точке частными
производными второго порядка.
51.
52.
53. Метод Лагранжа не имеет ограничений но является весьма трудоемким в практической реализации. По этой причине большое значение
приобретаютпрограммы, реализующие численные методы решения
задач
оптимизации.
Очень быстрый и эффективный способ численного
решения может быть реализован с помощью надстройки
Excel, которая называется «Поиск решения».
54. Численное решение задачи нелинейной оптимизации
55. Используем численный метод решения для проверки результатов, полученных методом Лагранжа в примере, рассмотренном ранее.
56.
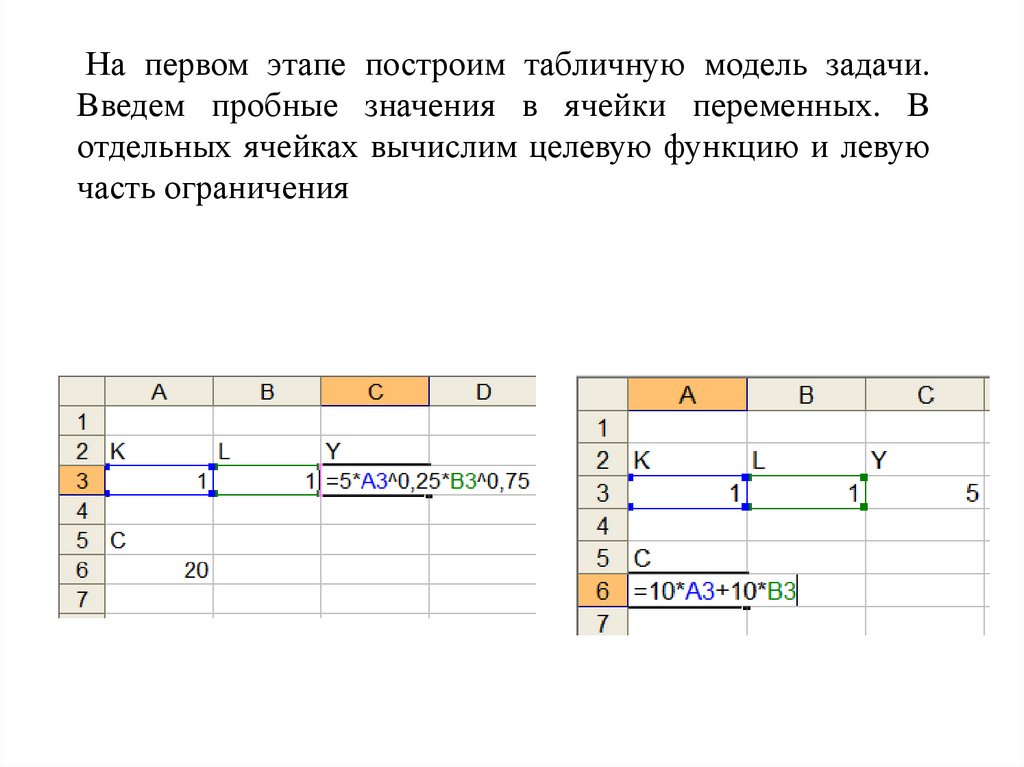
На первом этапе построим табличную модель задачи.Введем пробные значения в ячейки переменных. В
отдельных ячейках вычислим целевую функцию и левую
часть ограничения
57.
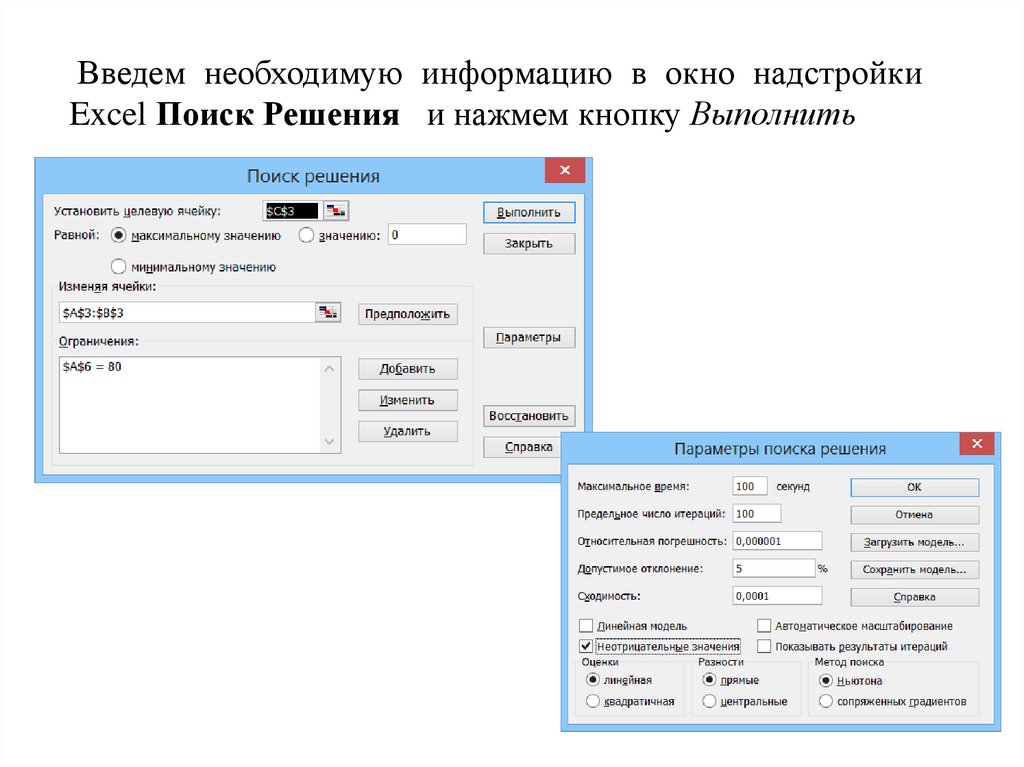
Введем необходимую информацию в окно надстройкиExcel Поиск Решения и нажмем кнопку Выполнить
58.
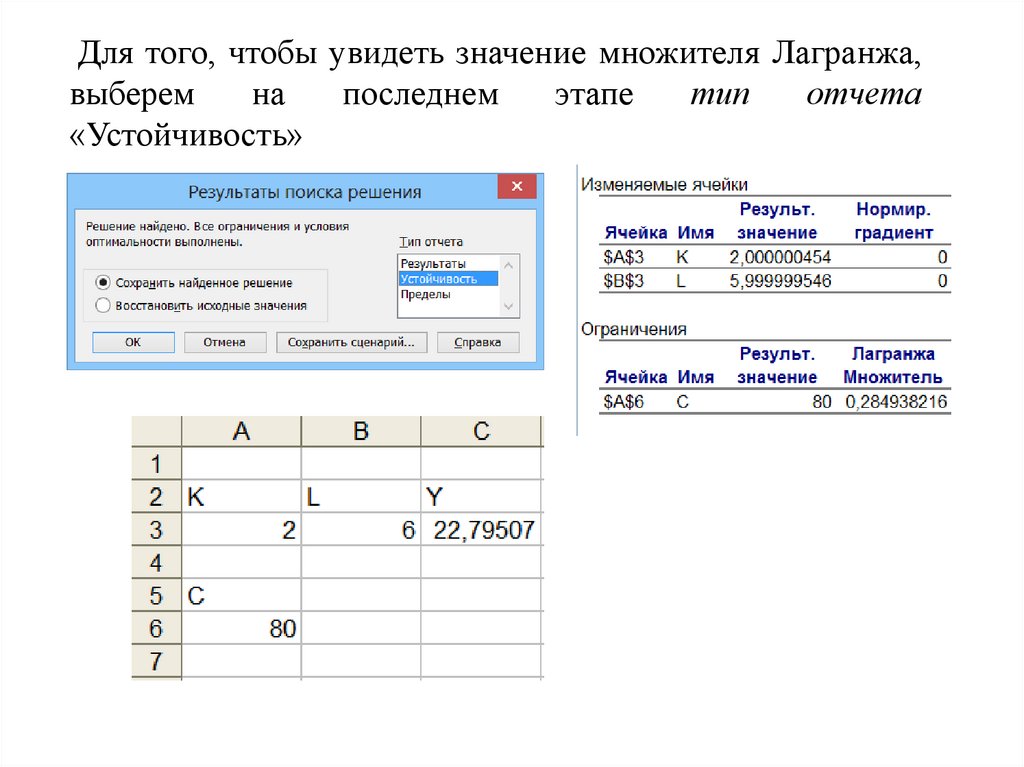
Для того, чтобы увидеть значение множителя Лагранжа,выберем
на
последнем
этапе
тип
отчета
«Устойчивость»
59. Основные параметры, которые вводятся в окно «Поиск решения» Целевая ячейка – вводится адрес ячейки, в которой вычисляется
целевая функцияИзменяемые ячейки – вводятся адреса ячеек с переменными
Ограничения –
в окно, открывающееся по команде Добавить вводятся:
в левой части - адрес ячейки с функцией ограничения,
в центре – знак ограничения,
в правой части – константа
60. На вкладке Параметры - устанавливается требование на неотрицательные значения переменных (практически всегда) - устанавливается
требование на линейность модели (длялинейных задач).
Значение в поле Сходимость используется для
завершения процесса поиска решения. Если изменение целевой
функции на протяжении пяти итераций меньше, чем указано в
окне, то процедура поиска решения завершает работу.
Поле Допустимое отклонение задает точность в
определении искомых переменных
Значение в поле Относительная погрешность
определяет, насколько точно левая часть должна
соответствовать правой части ограничения, чтобы ограничение
считалось выполненным как равенство.
61. На вкладке Параметры также расположены несколько полезных переключателей: Переключатель панели Оценки обычно (по умолчанию)
установлен в положение линейная. Квадратичная оценкаявляется более точной, но требует для выполнения вычислений
большего времени.
То же самое можно сказать и относительно установки
переключателей в поле Разности. Прямые разности
используются для гладких непрерывных функций, а
центральные – для функций, имеющих разрывную
производную. Последний способ точнее, но требует больше
вычислений.
При проведении оптимизации можно задать также
метод поиска решения. По умолчанию выбран метод Ньютона.
Альтернативный метод сопряженных градиентов требует
больших вычислений, однако для больших нелинейных задач
зачастую находит решение быстрее, нежели метод Ньютона.
62. Кнопка Сохранить модель позволяет задать ссылку на область ячеек, предназначенную для хранения модели оптимизации, а кнопка
Загрузить модель – задатьссылку на область ячеек, содержащих загружаемую
модель.
Эти возможности следует использовать, если на рабочем
листе располагается более чем одна оптимизационная
задача. Если на рабочем листе модель одна, то она
загружается автоматически.
63. Возможность решения задач нелинейной оптимизации численным методом
64. Нелинейные модели оптимизации - модели, в которых целевая функция или хотя бы одна из функций, входящих в ограничения, не
являютсялинейными.
Нелинейность целевой функции означает,
что у нее может быть несколько экстремумов
(локальных).
Глобальным
экстремумом
называется самый глубокий минимум (самый
высокий максимум) на области допустимых
решений.
65.
66.
67.
68.
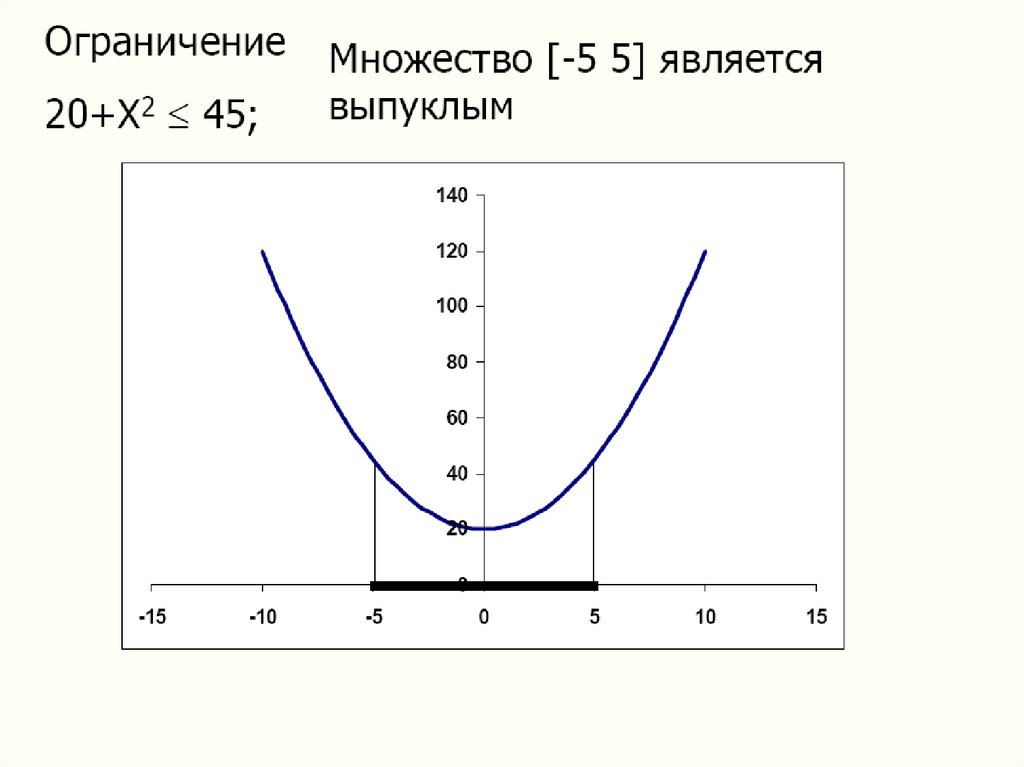
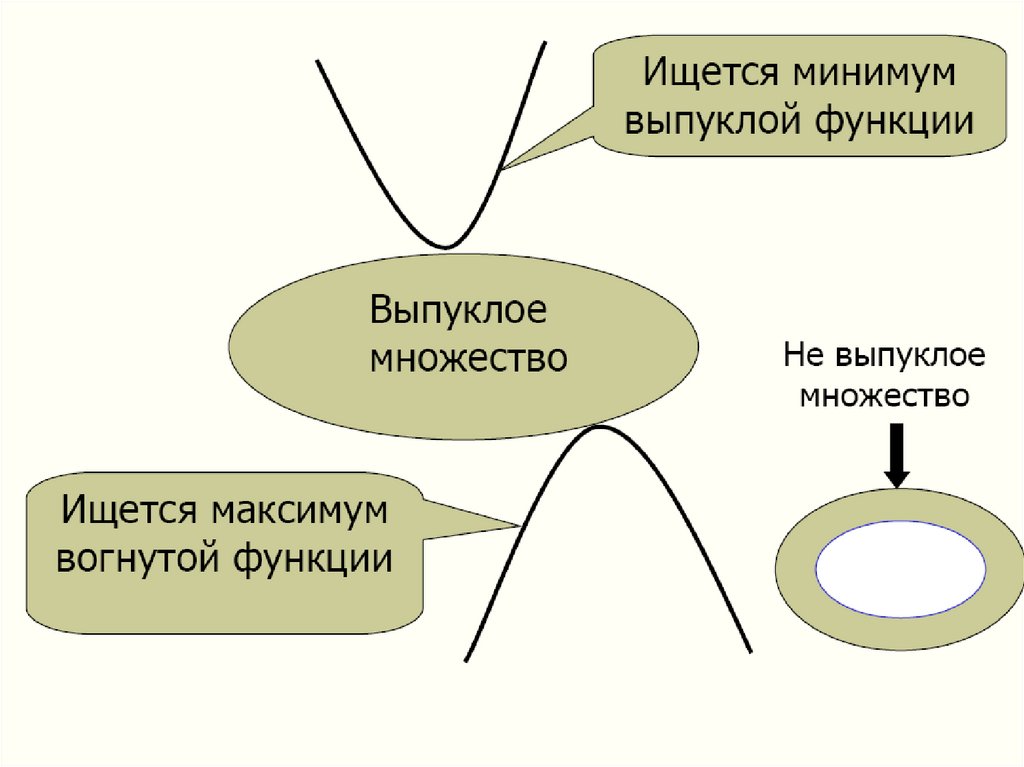
69. Оптимизации поддаются нелинейные задачи, в которых выполняется следующее условие: На выпуклом множестве ищется минимум выпуклой
функции или максимумвогнутой.
70.
71.
72.
73.
74.
75. Численное решение задач линейной оптимизации
76.
77.
78.
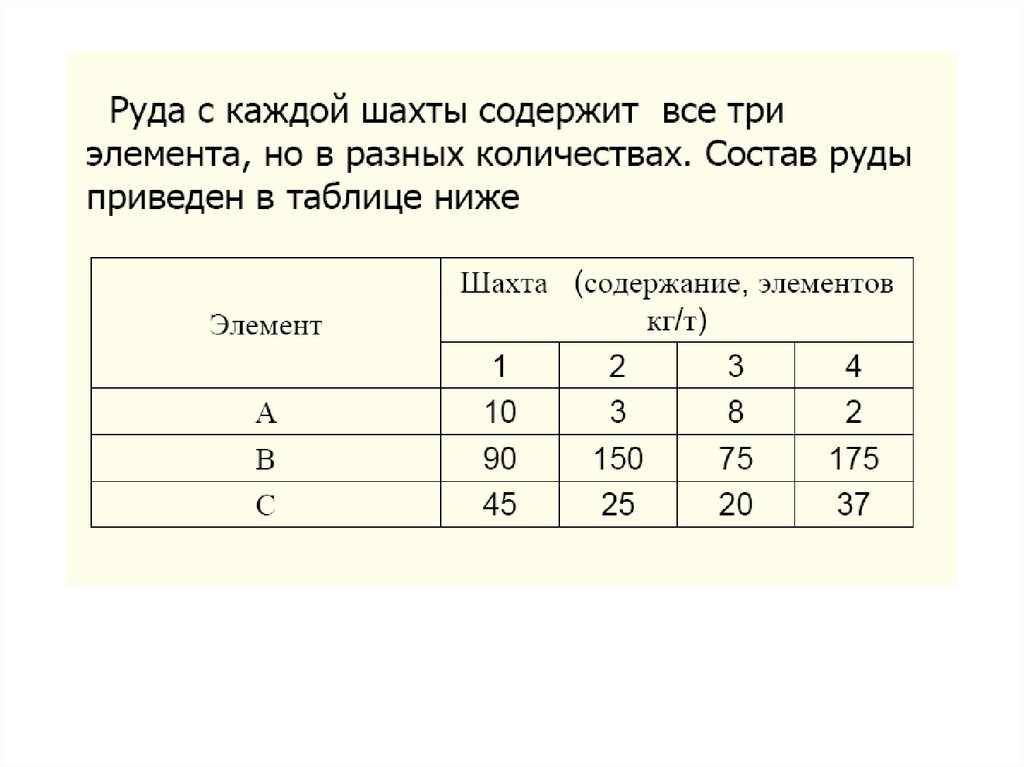
79.
80.
81.
82.
83.
84.
Полученная система уравнений содержит только линейныефункции, поэтому данную задачу следует отнести к задачам
линейного программирования.
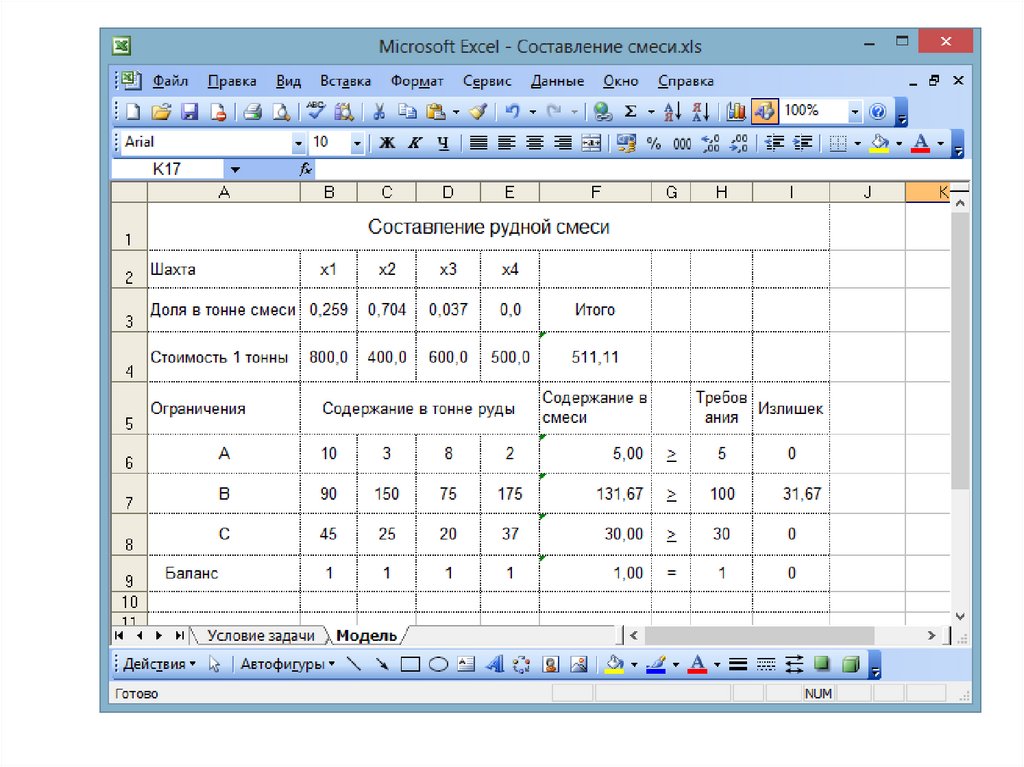
После того, как математическая модель готова, на листе Excel
необходимо построить табличную модель, позволяющую
рассчитывать целевую функцию и правые части ограничений при
заданных значениях переменных.
85.
86. Ограничения на неотрицательность переменных обычно не включаются в табличную модель, поскольку их можно задать с помощью
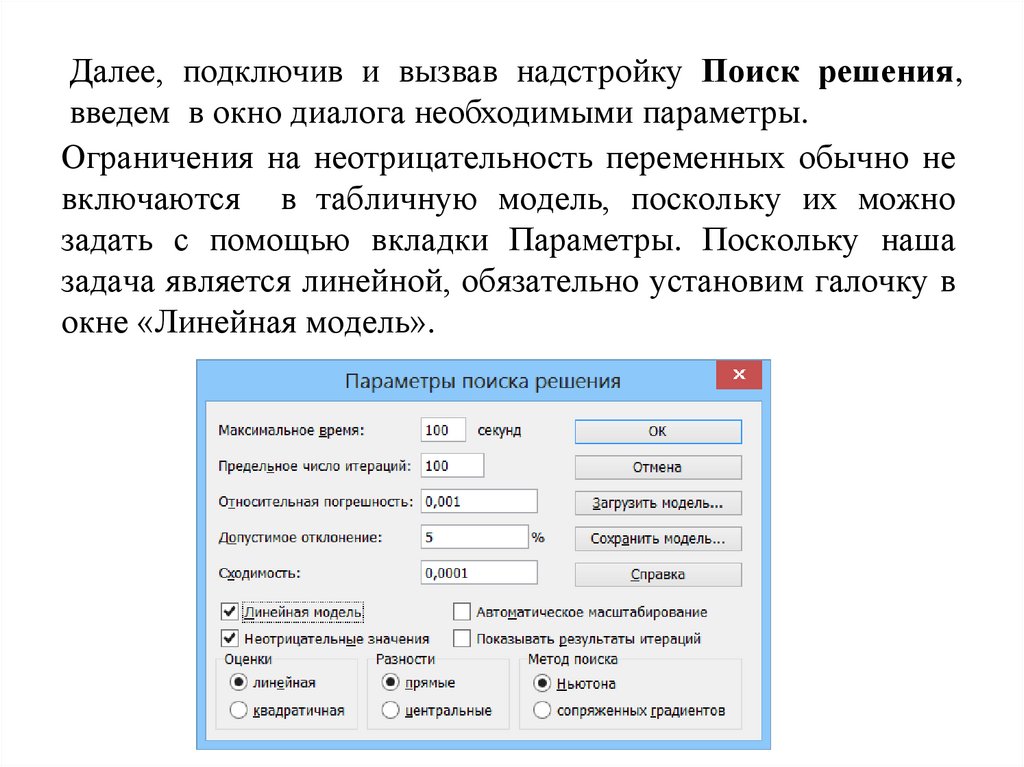
Далее, подключив и вызвав надстройку Поиск решения,введем в окно диалога необходимыми параметры.
Ограничения на неотрицательность переменных обычно не
включаются в табличную модель, поскольку их можно
задать с помощью вкладки Параметры. Поскольку наша
задача является линейной, обязательно установим галочку в
окне «Линейная модель».
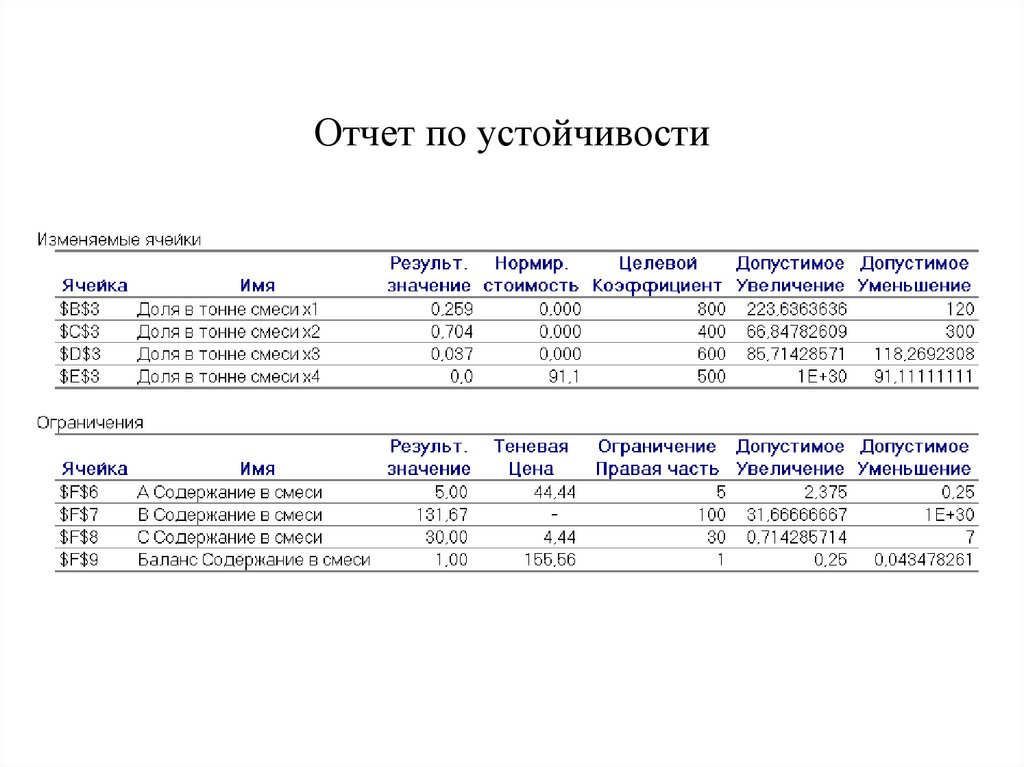
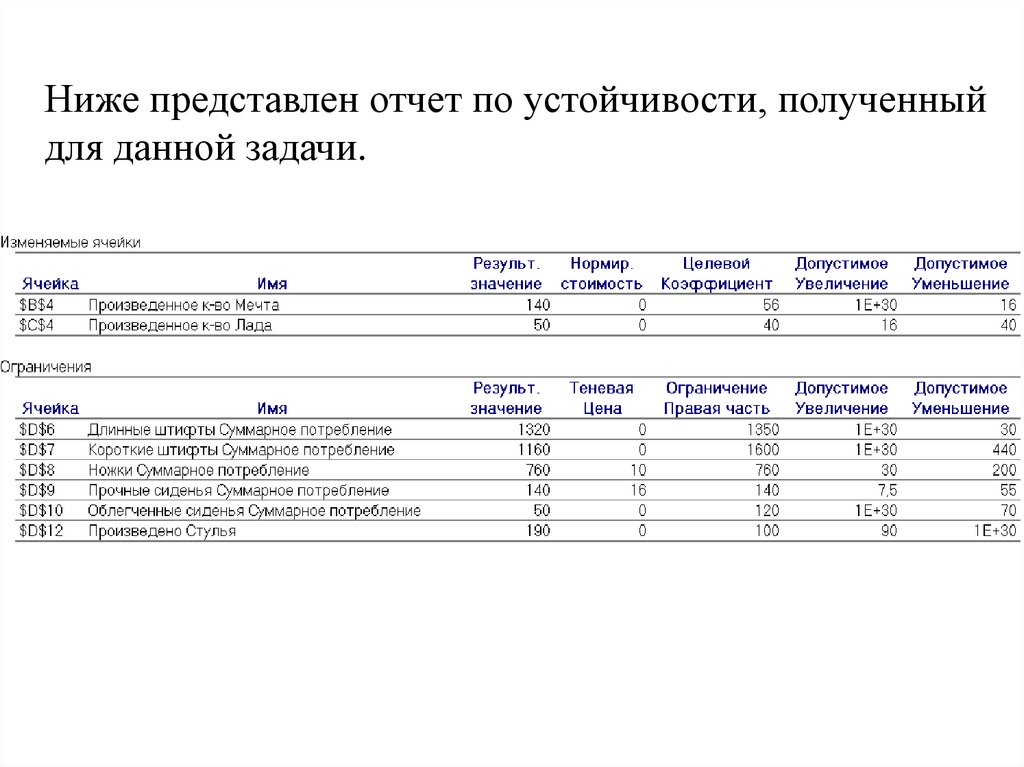
87. Отчет по устойчивости
88. После того, как все параметры введены, искомые значения переменных можно получить, нажав кнопку «Выполнить». При необходимости,
на этом этапе можнотакже вывести отчет по устойчивости, параметры
которого
зависят
от
вида
задачи.
Одним из наиболее важных параметров отчета по
устойчивости, который выводится для ограничений в
линейных задачах, является Теневая цена. Теневая цена
ограничения показывает, на какую величину изменится
целевая функция, если к правой части ограничения
прибавить единицу. В нелинейных задачах оптимизации
аналогом теневой цены является приводимый в отчетах
множитель Лагранжа.
89.
90.
91.
92. Графический метод решения задач линейной оптимизации
93.
94.
95.
96.
97.
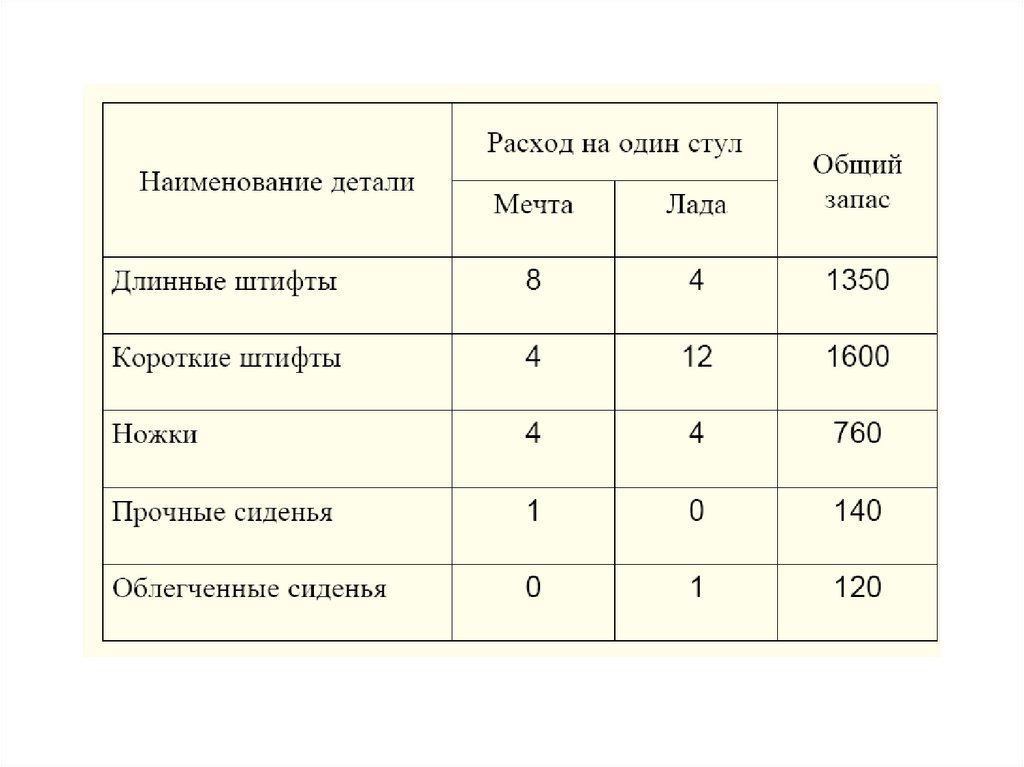
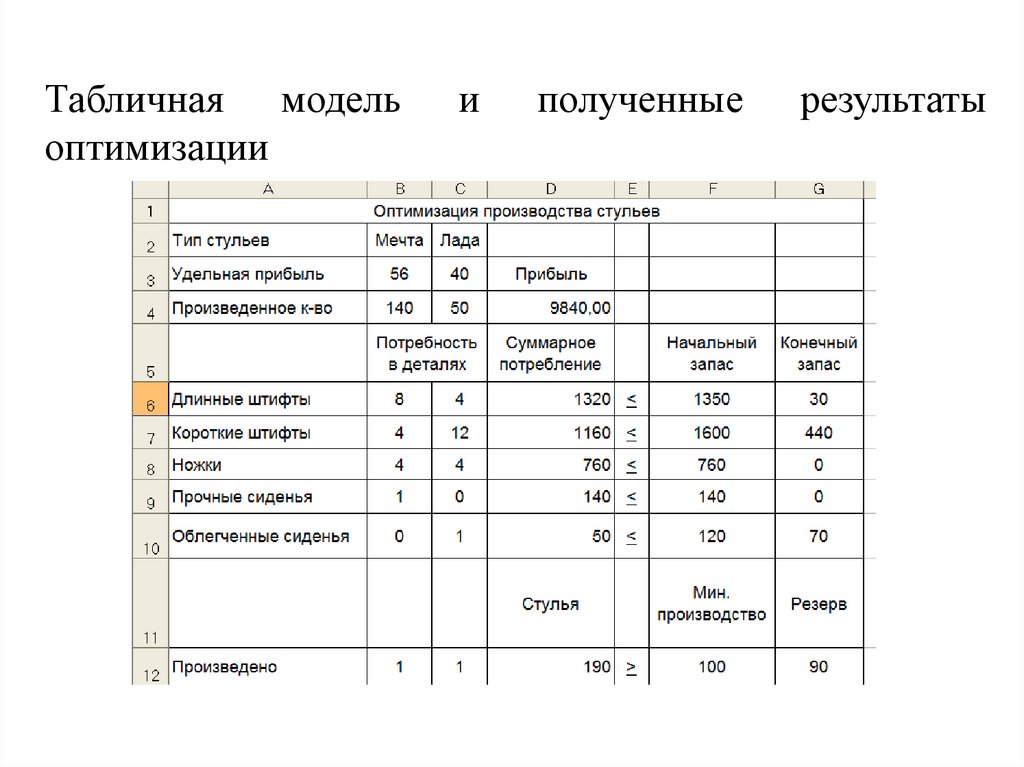
Табличная модельоптимизации
и
полученные
результаты
98.
Ниже представлен отчет по устойчивости, полученныйдля данной задачи.
99.
100.
101.
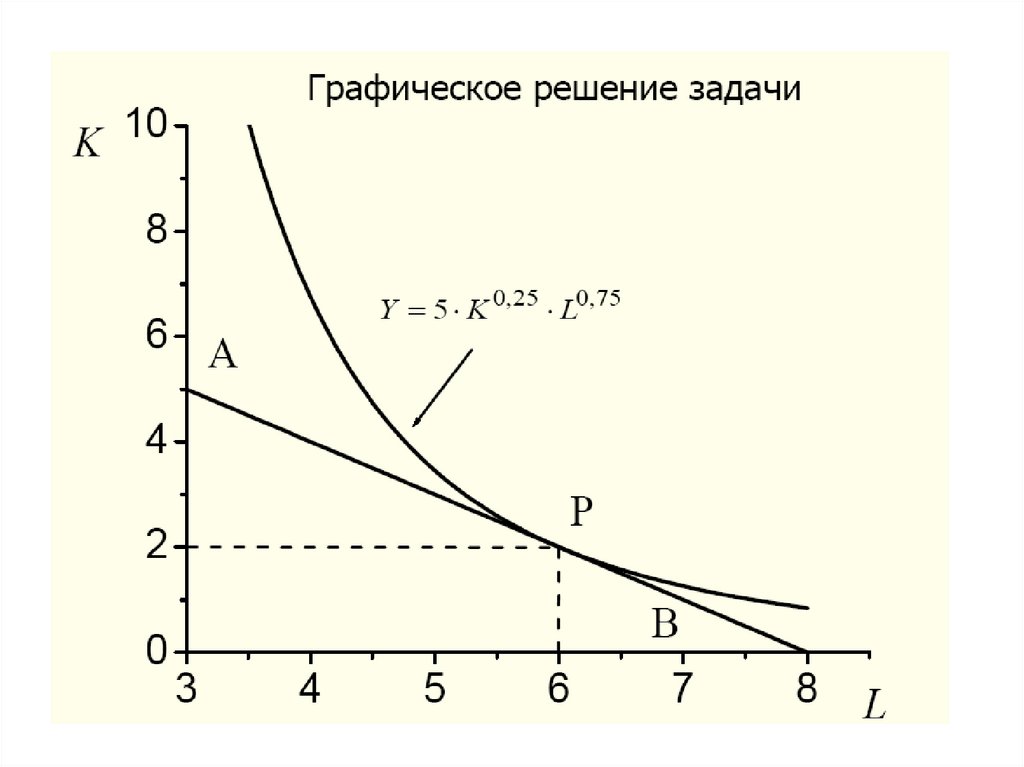
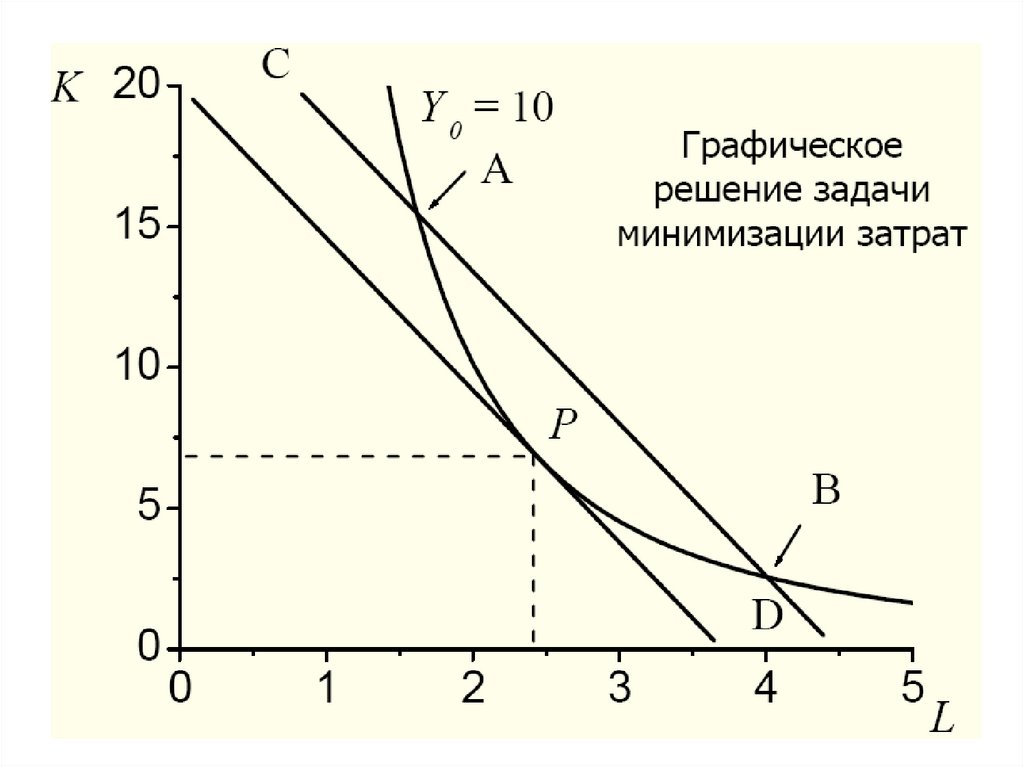
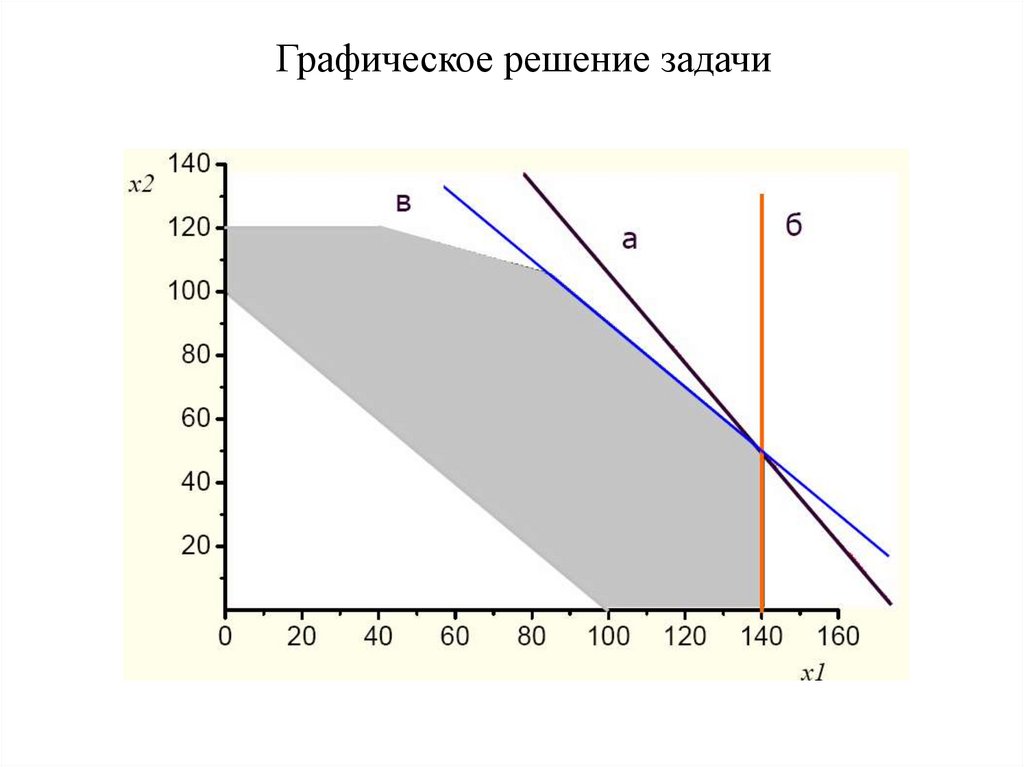
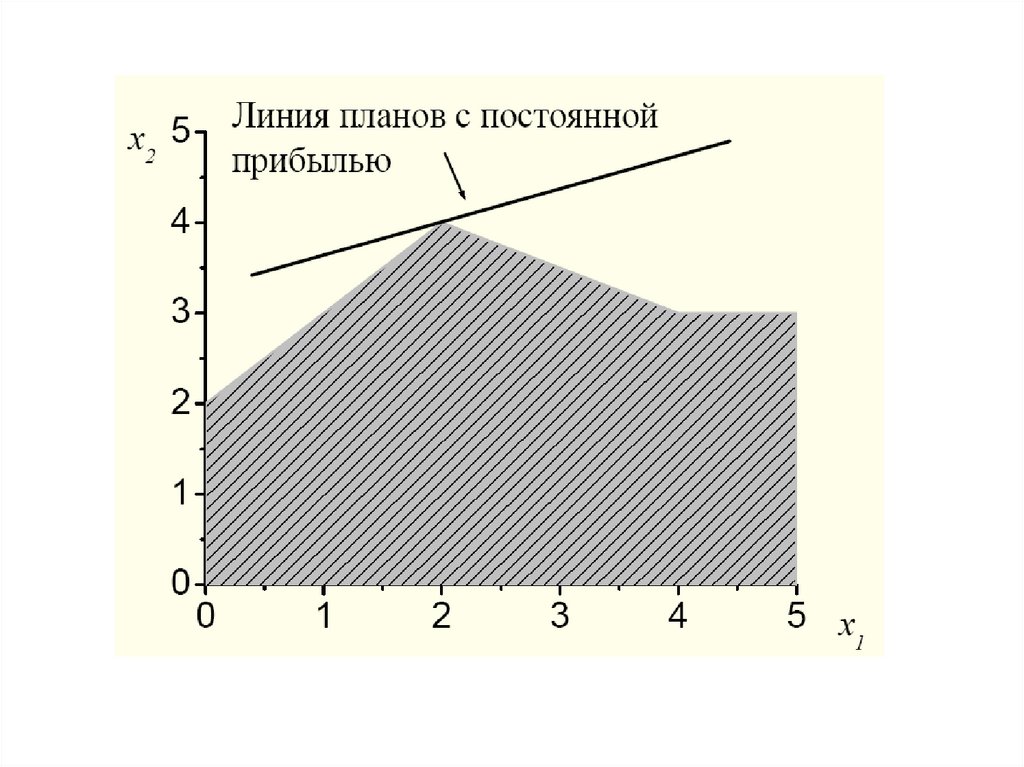
Графическое решение задачи102.
На рисунке, представленном на слайде, серымзакрашена область W допустимых значений (x1, x2) для
данной задачи. Границами области являются прямые,
уравнения которых получены заменой знака в
ограничениях модели на «равно». Точки пересечения
прямых называются угловыми точками области
допустимых значений.
Прямая
a
описывается
уравнением
56x1+40x2=9840, т.е. соответствует оптимальному
значению целевой функции при заданных по условию
целевых коэффициентах. Изменение константы в
уравнении не меняет наклона прямой, но приводит к ее
вертикальному смещению.
103.
104.
105.
На приведенном выше рисунке прямые б и всоответствуют возможным неустойчивым решениям,
появляющимся при новых
значениях целевых
коэффициентов, задающих наклон целевой функции,
совпадающий с наклоном прямой ограничения.
106. В моделях линейной оптимизации решение может находиться в угловой точке или совпадать с одним из ограничений. Решение
отсутствует в задачах, в которыхиз-за вида ограничений область допустимых
значений W оказалась пустой.
Решение может отсутствовать, если
область допустимых значений W оказалась
неограниченной.
В остальных случаях Excel обязательно
находит решение.



































































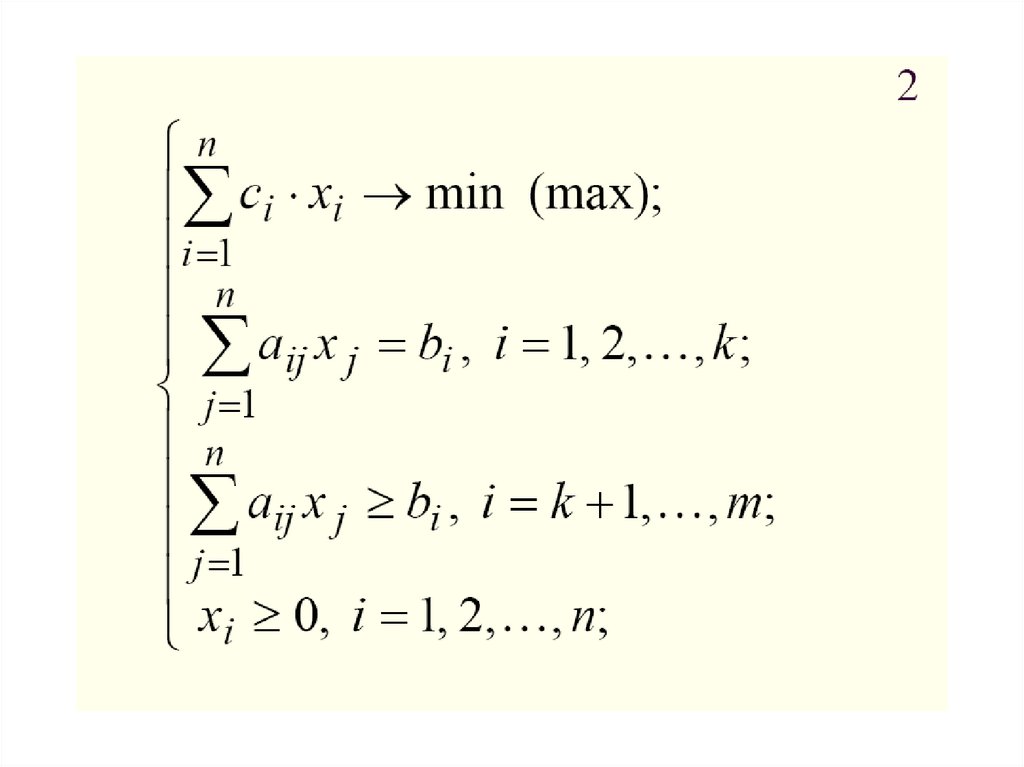



















 Математика
Математика Экономика
Экономика








