Похожие презентации:
Моделирование. §6. Модели и моделирование
1. Моделирование
1Моделирование
§ 6. Модели и моделирование
§ 7. Игровые модели
§ 8. Модели мышления
§ 9. Этапы моделирования
§ 10. Моделирование движения
§ 11. Математические модели в биологии
§ 12. Вероятностные модели
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
2. Моделирование
2Моделирование
§ 6. Модели и моделирование
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
3. Модели и моделирование
Моделирование, 11 класс3
Модели и моделирование
Модель – это объект, который обладает существенными
свойствами другого объекта, процесса или явления
(оригинала) и используется вместо него.
Моделирование – это создание и исследование моделей
с целью изучения оригиналов.
Задачи моделирования:
• исследование оригинала
• анализ («что будет, если …»)
• синтез («как сделать, чтобы …»)
• оптимизация («как сделать лучше всего …»)
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
4. Виды моделей (по природе)
Моделирование, 11 класс4
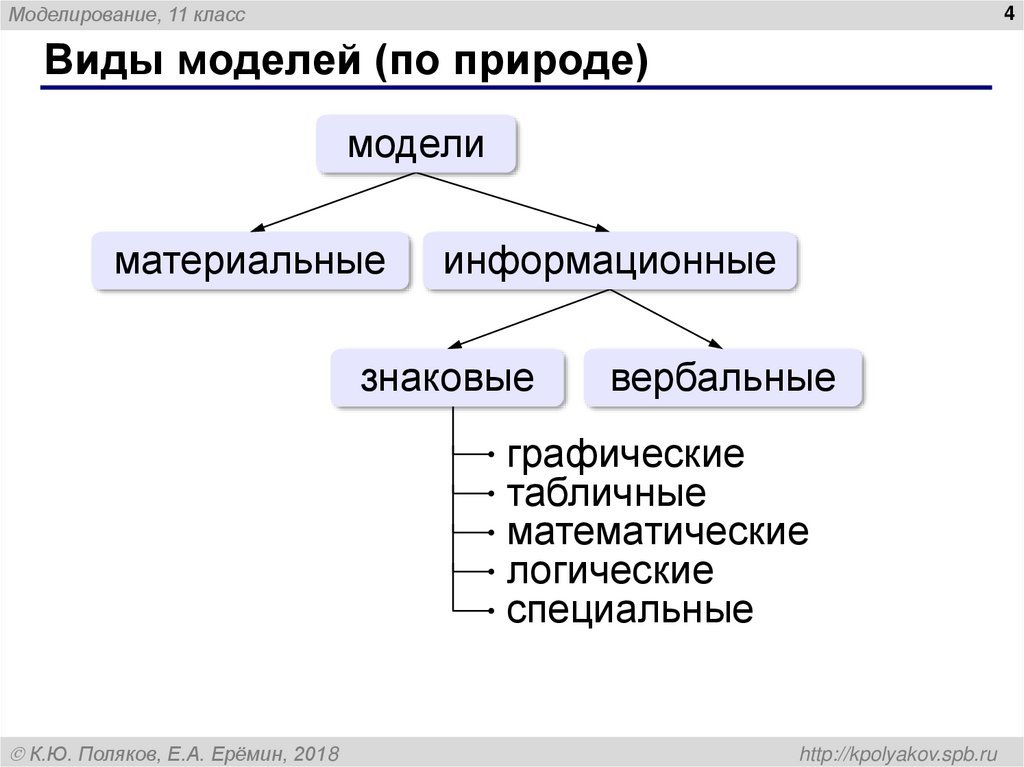
Виды моделей (по природе)
модели
материальные
информационные
знаковые
вербальные
графические
табличные
математические
логические
специальные
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
5. Виды моделей (по фактору времени)
Моделирование, 11 класс5
Виды моделей (по фактору времени)
• статические – описывают оригинал в заданный момент
времени
силы, действующие на тело в состоянии покоя
результаты осмотра врача
фотография
• динамические
модель движения тела
явления природы (молния, землетрясение, цунами)
история болезни
дискретные модели описывают
видеозапись события
поведение только в отдельные
…
моменты времени
непрерывные модели – в любой
момент времени
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
6. Виды моделей (по характеру связей)
Моделирование, 11 класс6
Виды моделей (по характеру связей)
• детерминированные – при одинаковых исходных
данных всегда получается тот же результат
расчёт по формулам
движение корабля на спокойной воде
…
• вероятностные – учитывают случайность событий
броуновское движение частиц
полета самолёта с учетом ветра
движения корабля на волнении
поведение человека
…
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
7. Виды динамических моделей
Моделирование, 11 класс7
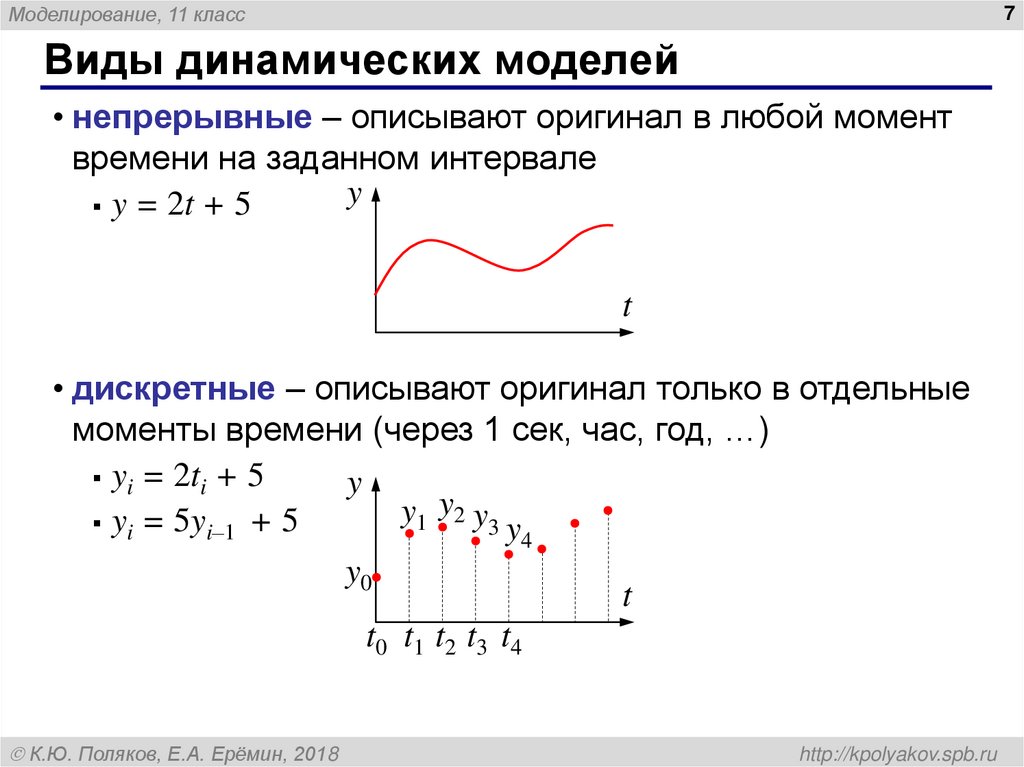
Виды динамических моделей
• непрерывные – описывают оригинал в любой момент
времени на заданном интервале
y
y = 2t + 5
t
• дискретные – описывают оригинал только в отдельные
моменты времени (через 1 сек, час, год, …)
yi = 2ti + 5
y
y1 y2 y3
yi = 5yi–1 + 5
y4
y0
t
t0 t1 t2 t3 t4
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
8. Имитационные модели
Моделирование, 11 класс8
Имитационные модели
• нельзя заранее вычислить или предсказать поведение
системы, но можно имитировать её реакцию на внешние
воздействия
• максимальный учет всех факторов
• только численные результаты
!
Задача – найти лучшее решение методом
проб и ошибок (многократные эксперименты)!
Примеры:
• испытания лекарств на мышах, обезьянах, …
• математическое моделирование биологических систем
• модели систем массового обслуживания
• модели процесса обучения
• кросс-программирование
•…
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
9. Игровые модели
Моделирование, 11 класс9
Игровые модели
Игровые модели учитывают действия противников.
• экономические ситуации
• военные действия
• спортивные игры
• тренинги персонала
!
Задача – найти лучший вариант действий в
самом худшем случае!
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
10. Иерархические модели
Моделирование, 11 класс10
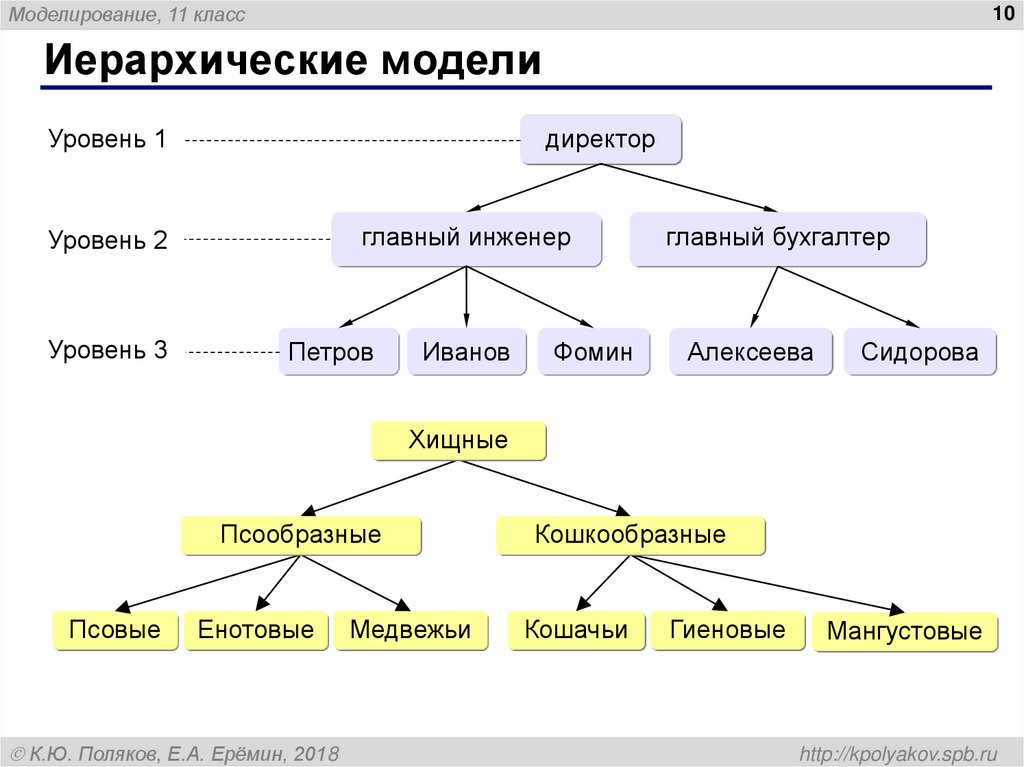
Иерархические модели
директор
Уровень 1
главный инженер
Уровень 2
Уровень 3
Петров
Иванов
Фомин
главный бухгалтер
Алексеева
Сидорова
Хищные
Псообразные
Псовые
Енотовые
К.Ю. Поляков, Е.А. Ерёмин, 2018
Медвежьи
Кошкообразные
Кошачьи
Гиеновые
Мангустовые
http://kpolyakov.spb.ru
11. Иерархические модели
Моделирование, 11 класс11
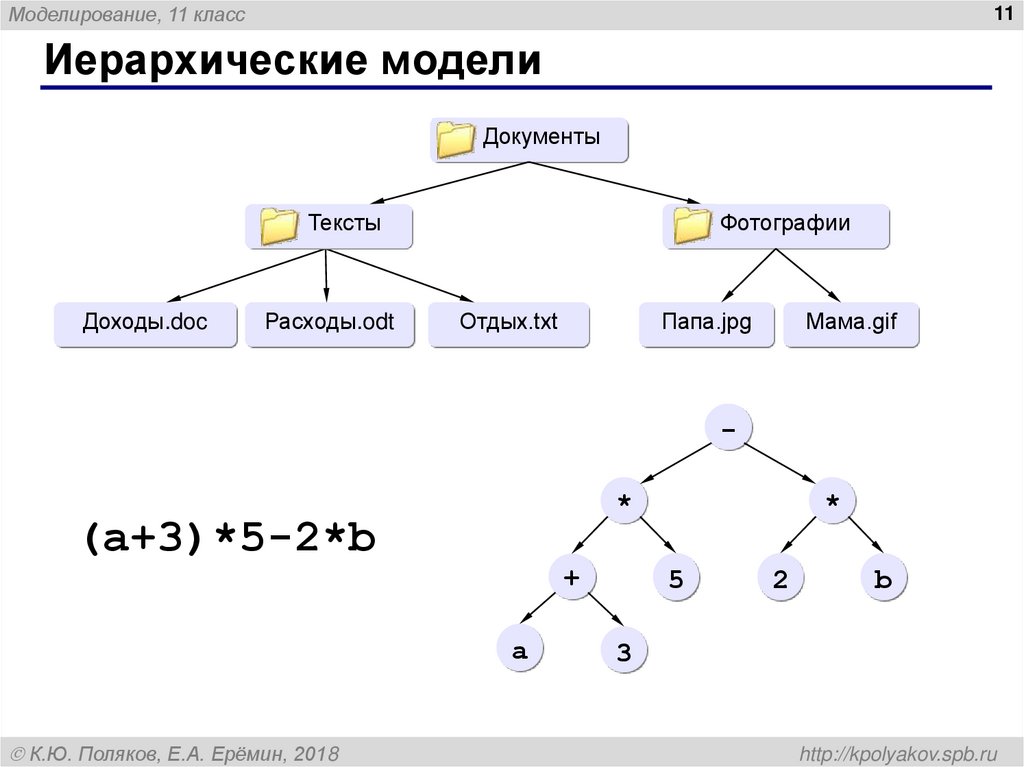
Иерархические модели
Документы
Тексты
Доходы.doc
Расходы.odt
Фотографии
Отдых.txt
Папа.jpg
Мама.gif
*
(a+3)*5-2*b
+
a
К.Ю. Поляков, Е.А. Ерёмин, 2018
*
5
2
b
3
http://kpolyakov.spb.ru
12. Сетевые модели
Моделирование, 11 класс12
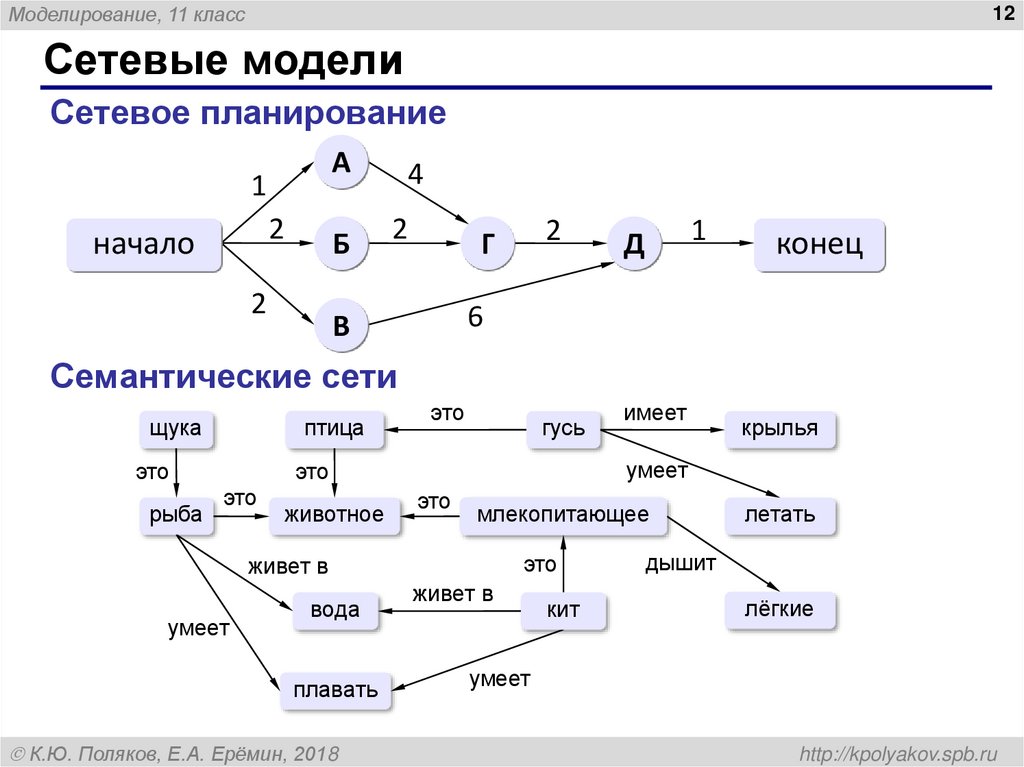
Сетевые модели
Сетевое планирование
1
2
начало
2
А
4
Б
2
2
Г
1
Д
конец
6
В
Семантические сети
щука
птица
это
это
рыба
это
животное
это
гусь
умеет
плавать
К.Ю. Поляков, Е.А. Ерёмин, 2018
крылья
умеет
это
млекопитающее
это
живет в
вода
имеет
живет в
кит
летать
дышит
лёгкие
умеет
http://kpolyakov.spb.ru
13. Задачи
Моделирование, 11 класс13
Задачи
Построить матрицы смежности и весовые матрицы.
5
4
A
D
A
E
1
1
3
1
3
C
B
D
C
B
2
3
1
2
E
3
5
A
E
2
4
3
B
C
D
1
2
К.Ю. Поляков, Е.А. Ерёмин, 2018
B
A
5
1
C
2
D
4
E
http://kpolyakov.spb.ru
14. Задачи
Моделирование, 11 класс14
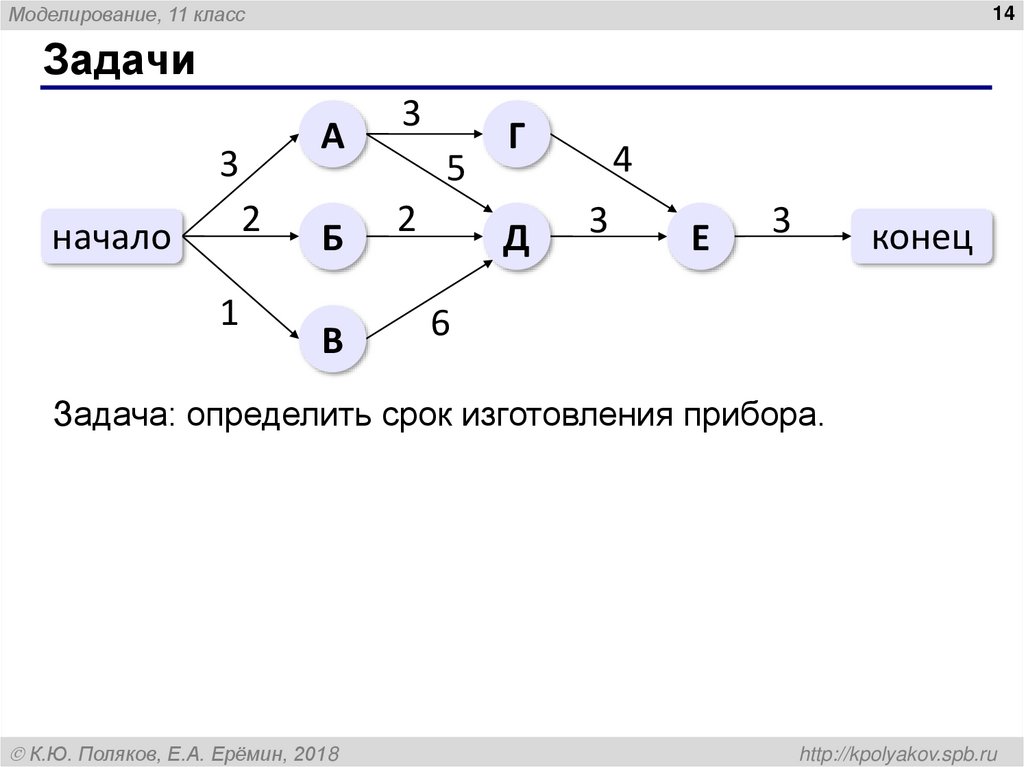
Задачи
А
3
2
начало
1
Б
В
3
5
2
Г
Д
4
3
Е
3
конец
6
Задача: определить срок изготовления прибора.
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
15. Адекватность
Моделирование, 11 класс15
Адекватность
Адекватность – это совпадение существенных свойств
модели и оригинала в данной задаче.
• результаты моделирования согласуются с выводами
теории (законы сохранения и т.п.)
• … подтверждаются экспериментом ( 10%)
!
Адекватность модели можно доказать только
экспериментом!
Модель всегда отличается от оригинала
!
Любая модель адекватна только при
определенных условиях!
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
16. Моделирование
16Моделирование
§ 7. Игровые модели
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
17. Игровые стратегии
Моделирование, 11 класс17
Игровые стратегии
? Какая задача?
Задача: найти стратегию (алгоритм игры), который
позволит получить лучший результат, если соперники
играют безошибочно.
Игры с полной информацией: можно определить, кто
должен выиграть, по начальной позиции.
Позиции:
• проигрышные – все возможные ходы ведут в
выигрышные позиции
• выигрышные – хотя бы один ход ведёт в
проигрышную позицию
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
18. Задача с кучей камней
Моделирование, 11 класс18
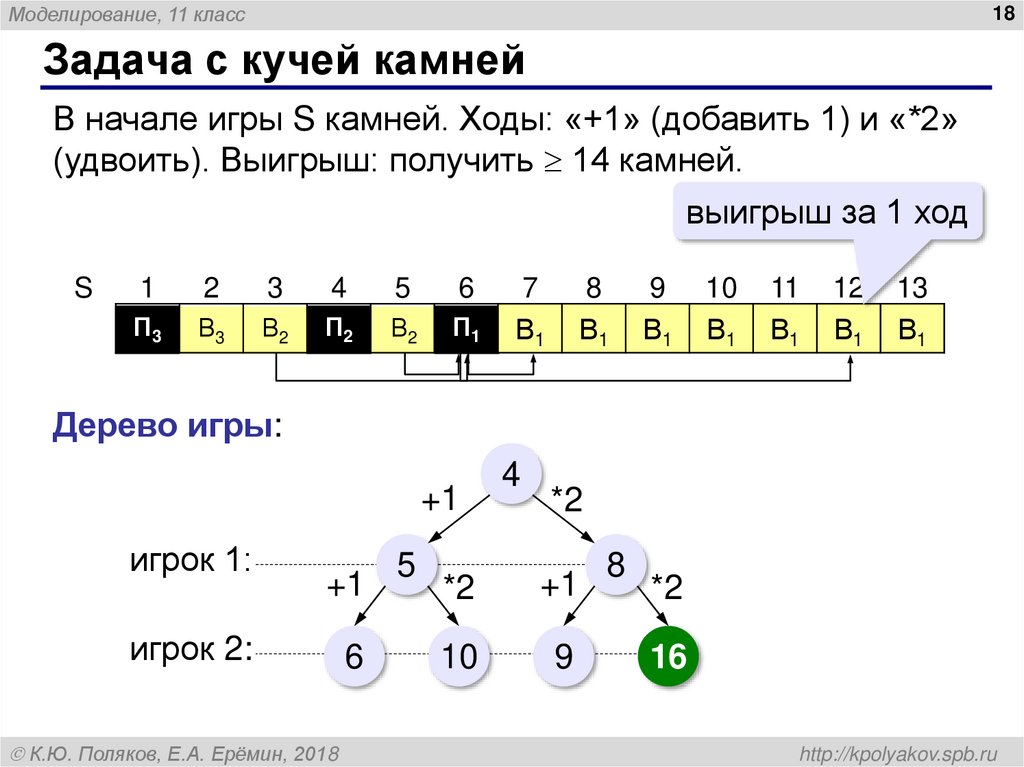
Задача с кучей камней
В начале игры S камней. Ходы: «+1» (добавить 1) и «*2»
(удвоить). Выигрыш: получить 14 камней.
выигрыш за 1 ход
S
1
2
3
4
5
6
П3
В3
В2
П2
В2
П1
7
В1
8
В1
9
В1
10
В1
11
В1
12
В1
13
В1
Дерево игры:
+1
игрок 1:
+1
игрок 2:
К.Ю. Поляков, Е.А. Ерёмин, 2018
6
5
4
*2
*2
+1
10
9
8
*2
16
http://kpolyakov.spb.ru
19. Неполное дерево игры
Моделирование, 11 класс19
Неполное дерево игры
Задача: доказать выигрыш какого-то игрока.
Для победителя – только 1 верный ход, для
проигравшего – все возможные ответы.
S
1
П3
?
2
B3
3
B2
4
П2
5
B2
6
П1
Какая стратегия
у игрока 2?
7
В1
8
В1
9
В1
10
В1
12
В1
13
В1
игрок 1:
4
+1
5
*2
8
+1
игрок 2:
переводить игру в
проигрышную (для
игрок 1:
соперника) позицию
игрок 2:
К.Ю. Поляков, Е.А. Ерёмин, 2018
11
В1
+1
7
*2
6
16
*2
12
*2
*2
14
24
http://kpolyakov.spb.ru
20. Задачи
Моделирование, 11 класс20
Задачи
1. В начале игры S камней. Ходы: «+2» (добавить 2) и
«*2» (удвоить). Выигрыш: получить 25 камней.
Построить дерево игры для S = 7.
2. В начале игры S камней. Ходы: «+1» (добавить 1) и
«*3» (утроить). Выигрыш: получить 55 камней.
Построить дерево игры для S = 16.
3. В начале игры S камней. Ходы: «+2» (добавить 2),
«+3» (добавить 3) и «*2» (удвоить). Выигрыш:
получить 30 камней.
Построить дерево игры для S = 9.
4. Игра Баше. В начале игры S (S 15) камней. Ходы:
«-1» (взять 1), «-2» (взять 2) и «-3» (взять 3).
Проигрыш: взять последний камень.
Построить дерево игры для S = 12.
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
21. Задача с двумя кучами камней
Моделирование, 11 класс21
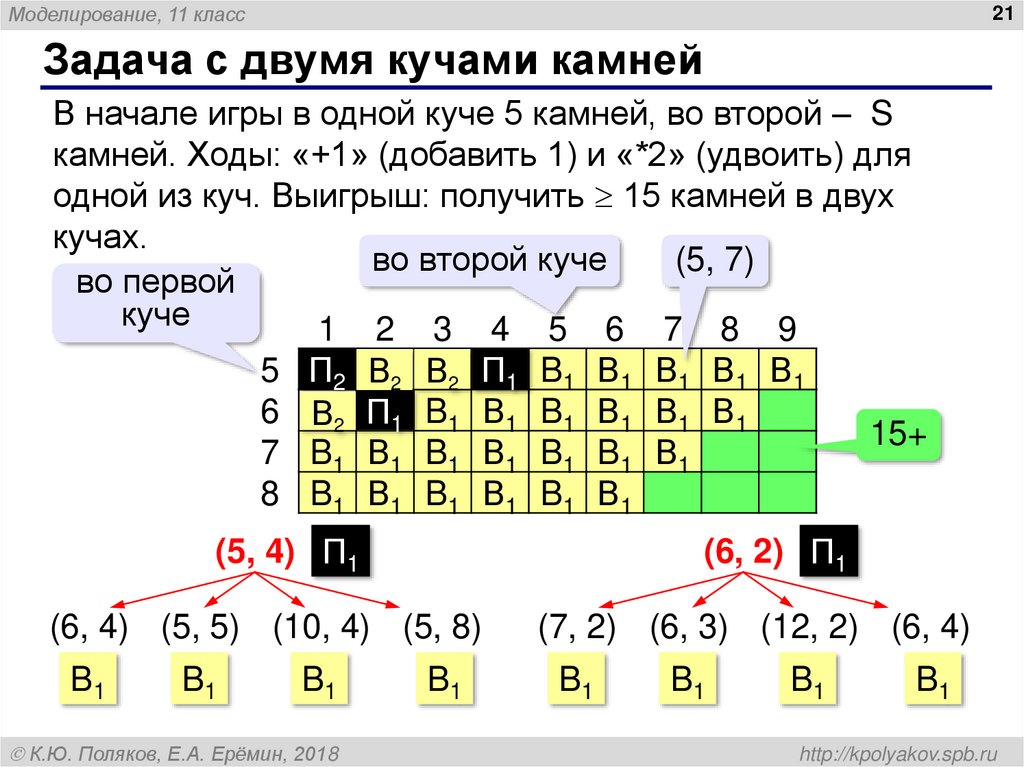
Задача с двумя кучами камней
В начале игры в одной куче 5 камней, во второй – S
камней. Ходы: «+1» (добавить 1) и «*2» (удвоить) для
одной из куч. Выигрыш: получить 15 камней в двух
кучах.
во второй куче
(5, 7)
во первой
куче
1 2 3 4 5 6 7 8 9
?1 B1 В1 В1 В1 В1
5 П2 В2 В2 П
6 В2 П?1 B1 В1 B1 В1 В1 В1
15+
7 B1 В1 B1 В1 B1 B1 В1
8 B1 В1 B1 В1 B1 В1
(5, 4) П1
(6, 2) П1
(6, 4) (5, 5) (10, 4) (5, 8)
(7, 2) (6, 3) (12, 2) (6, 4)
B1
B1
B1
B1
К.Ю. Поляков, Е.А. Ерёмин, 2018
B1
B1
B1
B1
http://kpolyakov.spb.ru
22. Неполное дерево игры
Моделирование, 11 класс22
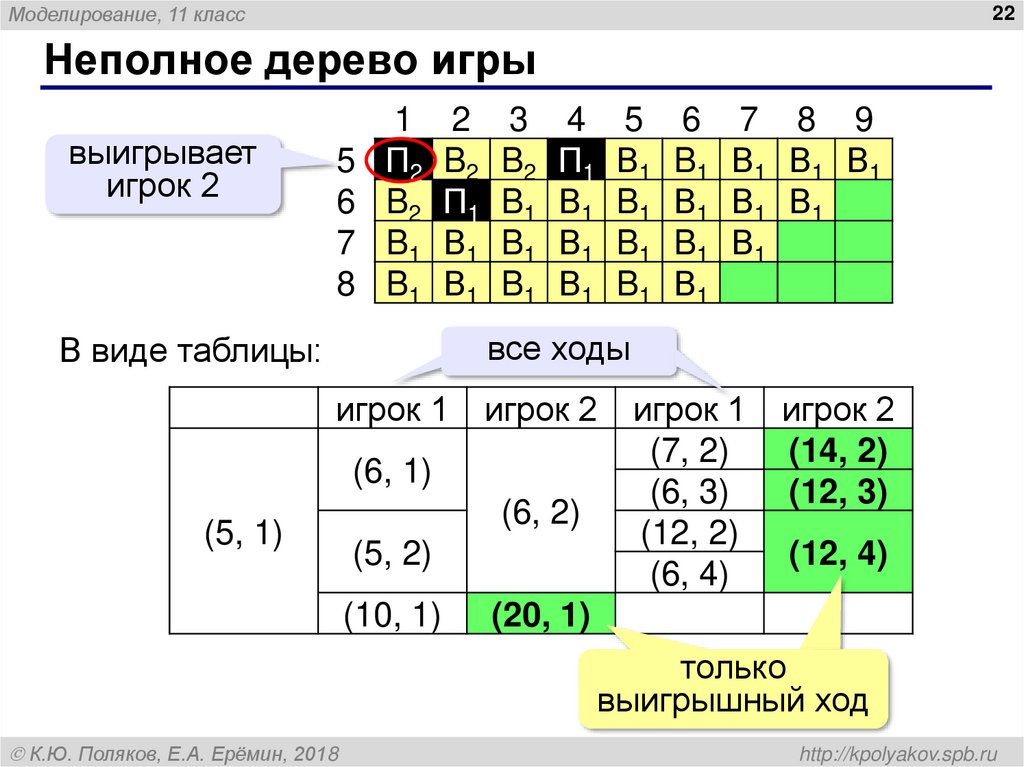
Неполное дерево игры
выигрывает
игрок 2
5
6
7
8
1 2 3 4 5 6 7 8 9
П2 B2 B2 П1 В1 B1 В1 В1 В1
B2 П1 B1 В1 B1 В1 В1 В1
B1 В1 B1 В1 B1 B1 В1
B1 В1 B1 В1 B1 В1
все ходы
В виде таблицы:
игрок 1
игрок 2
(6, 1)
(5, 1)
(6, 2)
(5, 2)
(10, 1)
игрок 1
(7, 2)
(6, 3)
(12, 2)
(6, 4)
игрок 2
(14, 2)
(12, 3)
(12, 4)
(20, 1)
только
выигрышный ход
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
23. Моделирование
23Моделирование
§ 8. Модели мышления
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
24. Искусственный интеллект
Моделирование, 11 класс24
Искусственный интеллект
Задача: моделирование мышления человека для
решения сложных задач, которые не удаётся решить
алгоритмически.
• экспертные системы
моделируют ход рассуждений человека-эксперта при
принятии решений в сложных ситуациях:
ЕСЛИ у человека повышенная температура
ТО он нездоров
дедукция: от общих принципов к конкретному случаю
• нейрокомпьютеры (нейросети)
поиск алгоритмов решения на основе анализа многих
частных случаев (обучение)
индукция: от конкретных случаев к общему правилу
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
25. Модель нейрона
Моделирование, 11 класс25
Модель нейрона
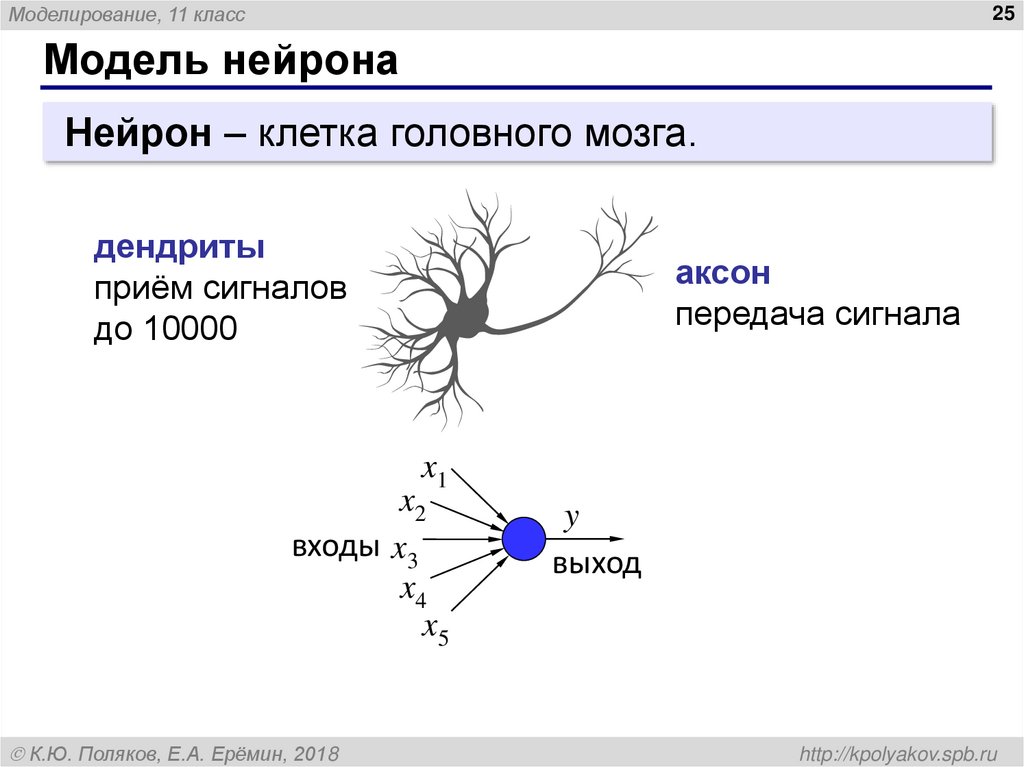
Нейрон – клетка головного мозга.
дендриты
приём сигналов
до 10000
аксон
передача сигнала
x1
x2
входы x3
x4
x5
К.Ю. Поляков, Е.А. Ерёмин, 2018
y
выход
http://kpolyakov.spb.ru
26. Модель нейрона
Моделирование, 11 класс26
Модель нейрона
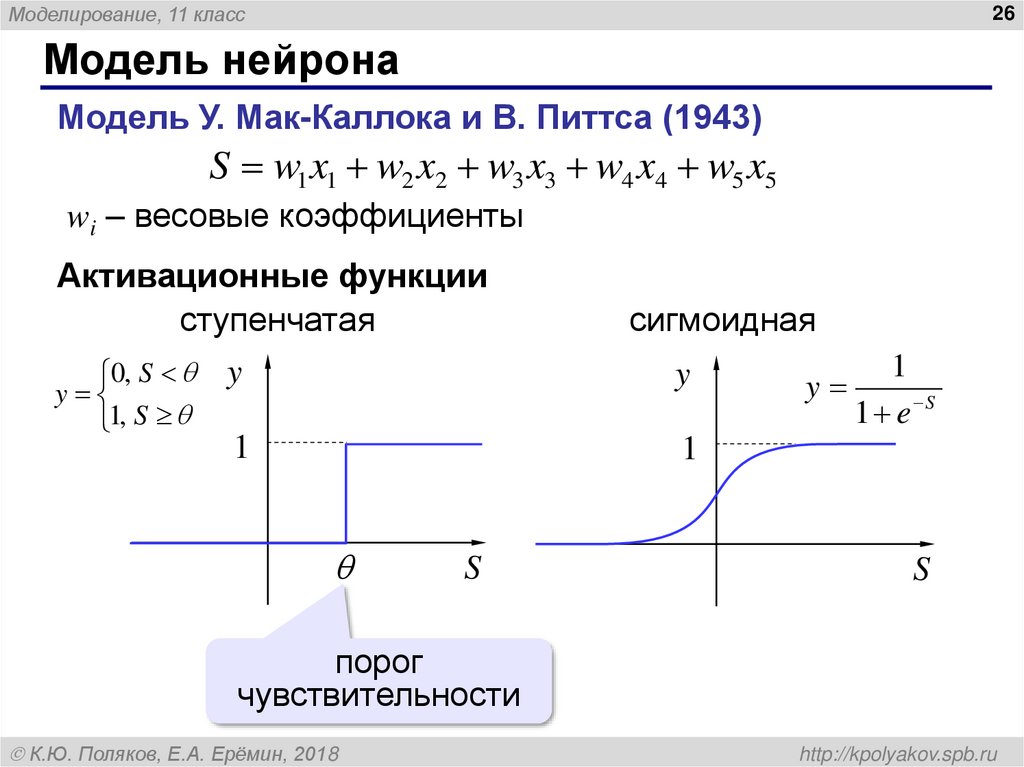
Модель У. Мак-Каллока и В. Питтса (1943)
S w1 x1 w2 x2 w3 x3 w4 x4 w5 x5
wi – весовые коэффициенты
Активационные функции
ступенчатая
0, S
y
1, S
сигмоидная
y
y
1
1
S
y
1
1 e S
S
порог
чувствительности
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
27. Персептрон
Моделирование, 11 класс27
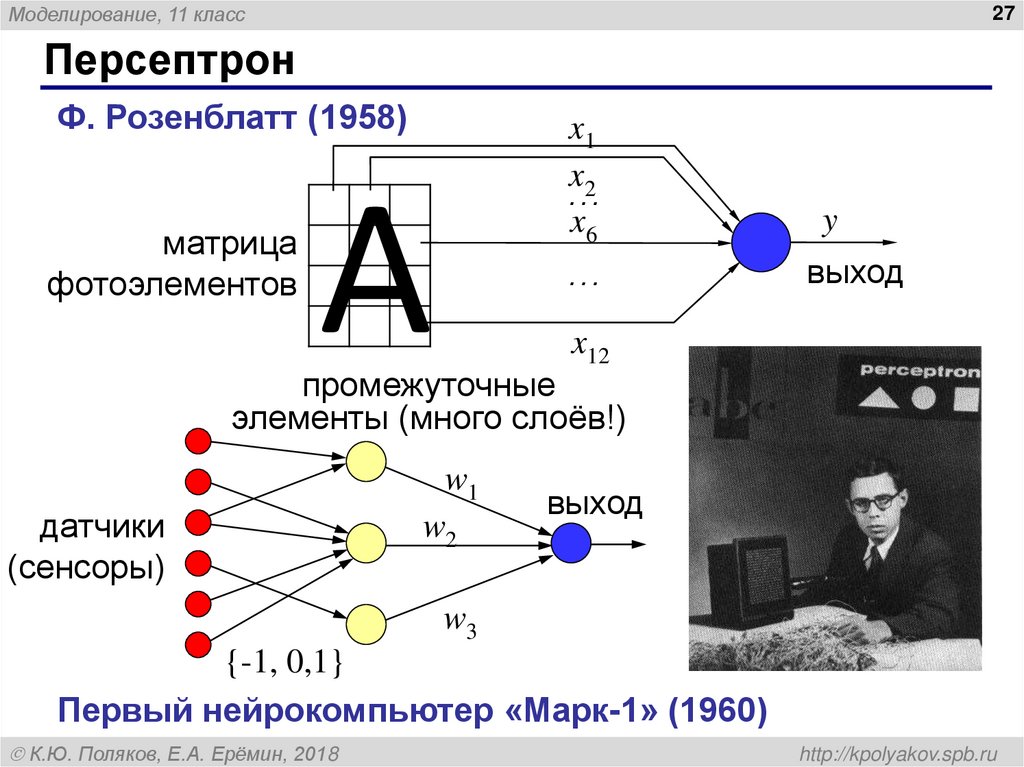
Персептрон
Ф. Розенблатт (1958)
матрица
фотоэлементов
А
x1
x2
…
x6
y
…
выход
x12
промежуточные
элементы (много слоёв!)
датчики
(сенсоры)
w1
w2
выход
w3
{-1, 0,1}
Первый нейрокомпьютер «Марк-1» (1960)
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
28. Обучение нейронной сети
Моделирование, 11 класс28
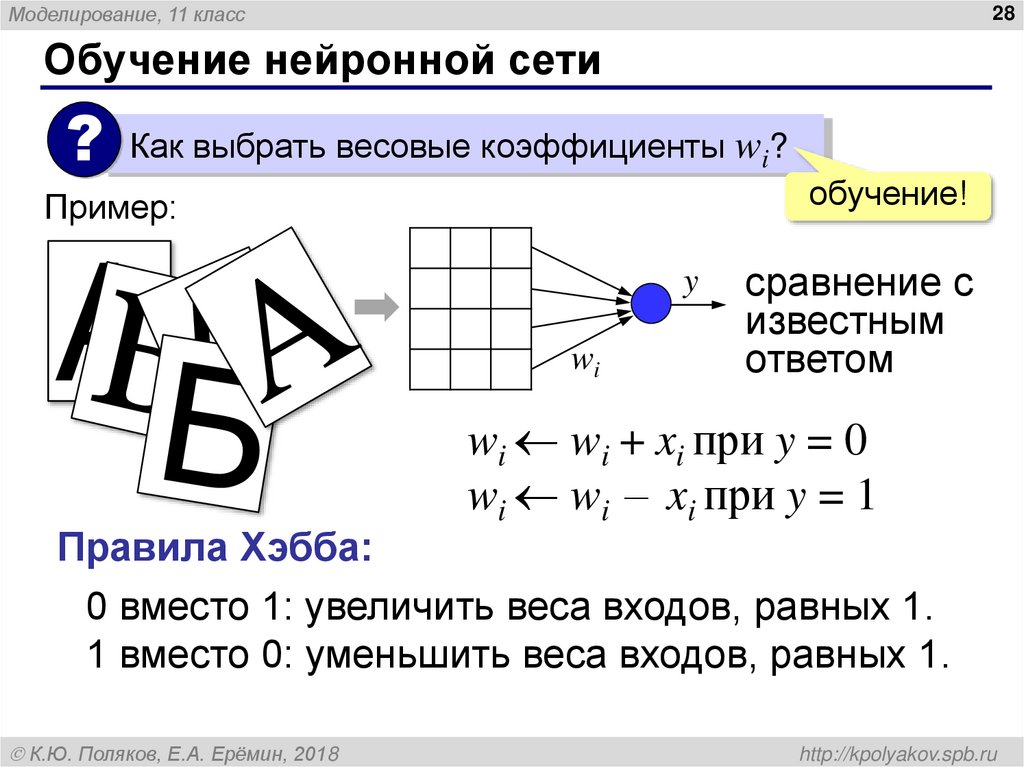
Обучение нейронной сети
? Как выбрать весовые коэффициенты wi?
обучение!
Пример:
А
y
wi
сравнение с
известным
ответом
wi wi + xi при y = 0
wi wi – xi при y = 1
Правила Хэбба:
0 вместо 1: увеличить веса входов, равных 1.
1 вместо 0: уменьшить веса входов, равных 1.
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
29. Применение нейронных сетей
Моделирование, 11 класс29
Применение нейронных сетей
много примеров, но нет теории (алгоритма)
• распознавание (лиц, голосов, отпечатков
пальцев)
• классификация (платёжеспособность
клиента, проверка подлинности подписи,
постановка диагноза)
• прогнозирование (курсов валют, цен на
сырьё)
МЧС РФ
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
30. Раскрашивание фотографий
Моделирование, 11 класс30
Раскрашивание фотографий
чёрно-белое фото
это сделала нейронная сеть
цветное фото
color.artlebedev.ru
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
31. Интеллектуальные игры
Моделирование, 11 класс31
Интеллектуальные игры
игра «го»
Google DeepMind
1:4
Ли Седоль
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
32. Беспилотные автомобили
Моделирование, 11 класс32
Беспилотные автомобили
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
33. Нейронные сети: итоги
Моделирование, 11 класс33
Нейронные сети: итоги
могут работать при неопределенности данных, в
условиях помех
обрабатывают информацию параллельно
способны самообучаться
не используют и не выявляют законы
природы
не могут объяснить результат
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
34. Машинное обучение
Моделирование, 11 класс34
Машинное обучение
Machine Learning
? Накоплено много данных. Как сделать выводы?
Задача машинного обучения – разработка
автоматических методов анализа данных и
извлечения из них каких-то закономерностей.
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
35. Задача классификации
Моделирование, 11 класс35
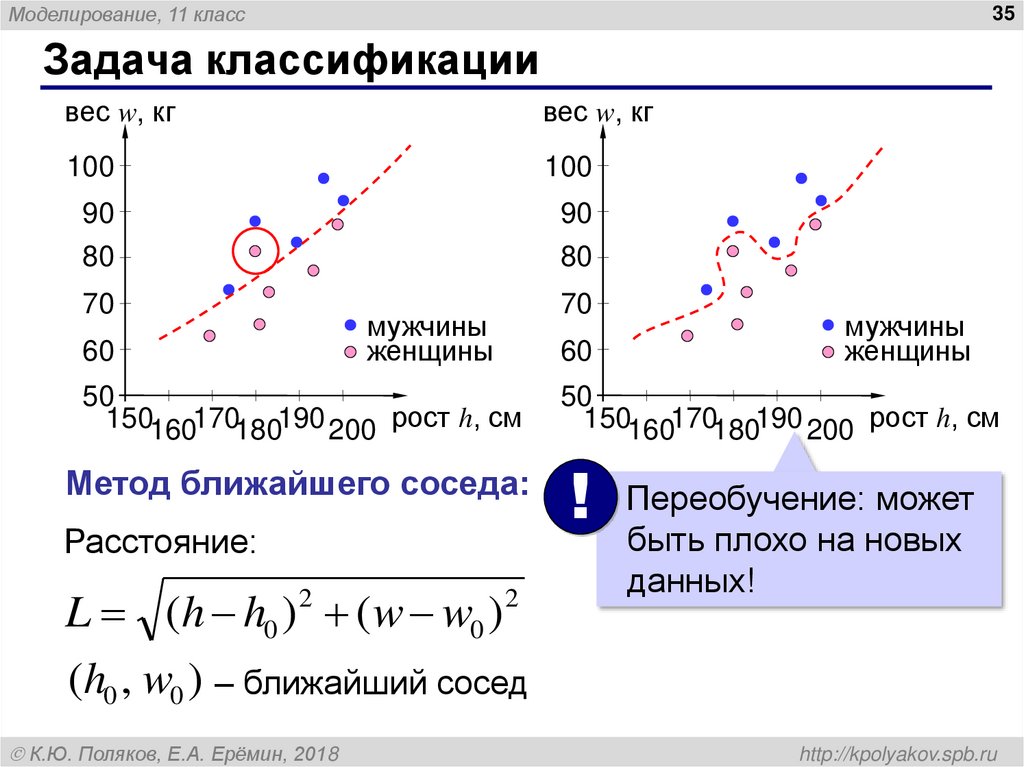
Задача классификации
вес w, кг
вес w, кг
100
100
90
80
90
80
70
70
мужчины
женщины
60
60
мужчины
женщины
50
150160170180190 200 рост h, см
50
150160170180190 200 рост h, см
Метод ближайшего соседа:
! Переобучение: может
Расстояние:
L (h h0 ) (w w0 )
(h0 , w0 ) – ближайший сосед
2
К.Ю. Поляков, Е.А. Ерёмин, 2018
2
быть плохо на новых
данных!
http://kpolyakov.spb.ru
36. Дерево решений
Моделирование, 11 класс36
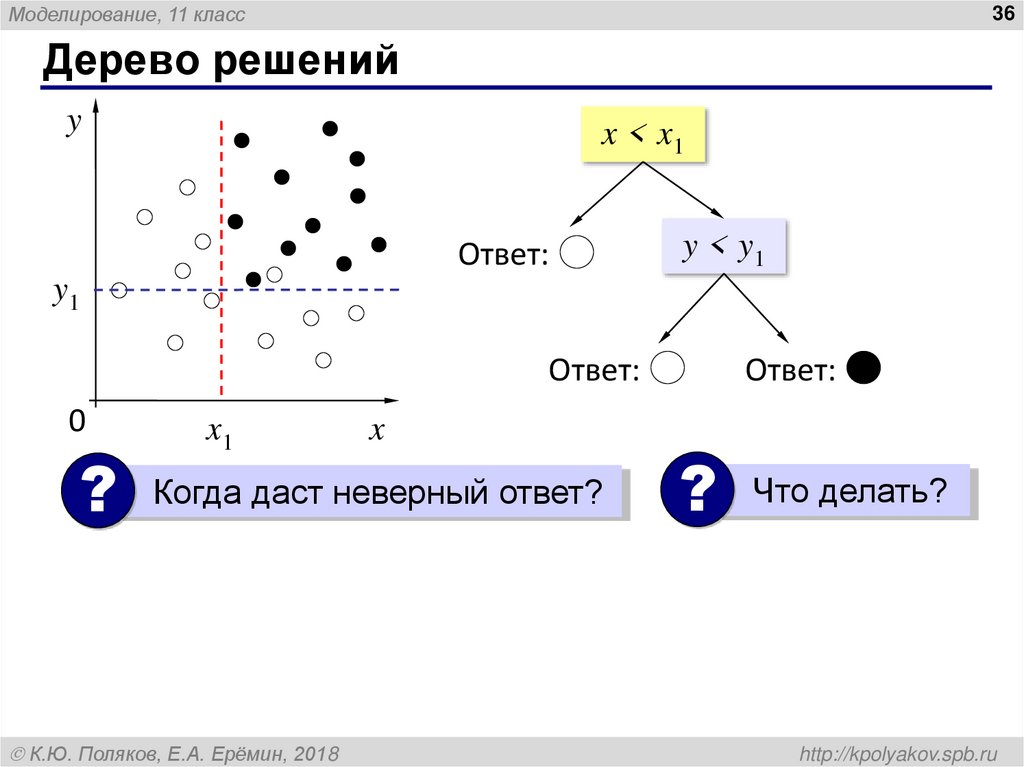
Дерево решений
y
x < x1
Ответ:
y < y1
y1
Ответ:
0
x1
x
? Когда даст неверный ответ?
К.Ю. Поляков, Е.А. Ерёмин, 2018
Ответ:
? Что делать?
http://kpolyakov.spb.ru
37. Применение машинного обучения
Моделирование, 11 класс37
Применение машинного обучения
• классификация
• распознавания образов
• предсказание
• анализ текстов
• машинный перевод
• ранжирование страниц в поисковых системах
• рекомендации (музыка, реклама)
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
38. Большие данные (Big Data)
Моделирование, 11 класс38
Большие данные (Big Data)
• имеют очень большой объём (терабайты и
петабайты);
• не могут храниться и обрабатываться на одном
компьютере.
Серверы Google: > 24 Пбайт в день
Часто такие данные
• поступают с большой скоростью (мегабайты
и гигагабайты в секунду)
• очень разнообразны (числа, графика, видео)
Решение:
• распределённые базы данных
• кластеры для параллельной обработки
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
39. Алгоритм Map-Reduce
Моделирование, 11 класс39
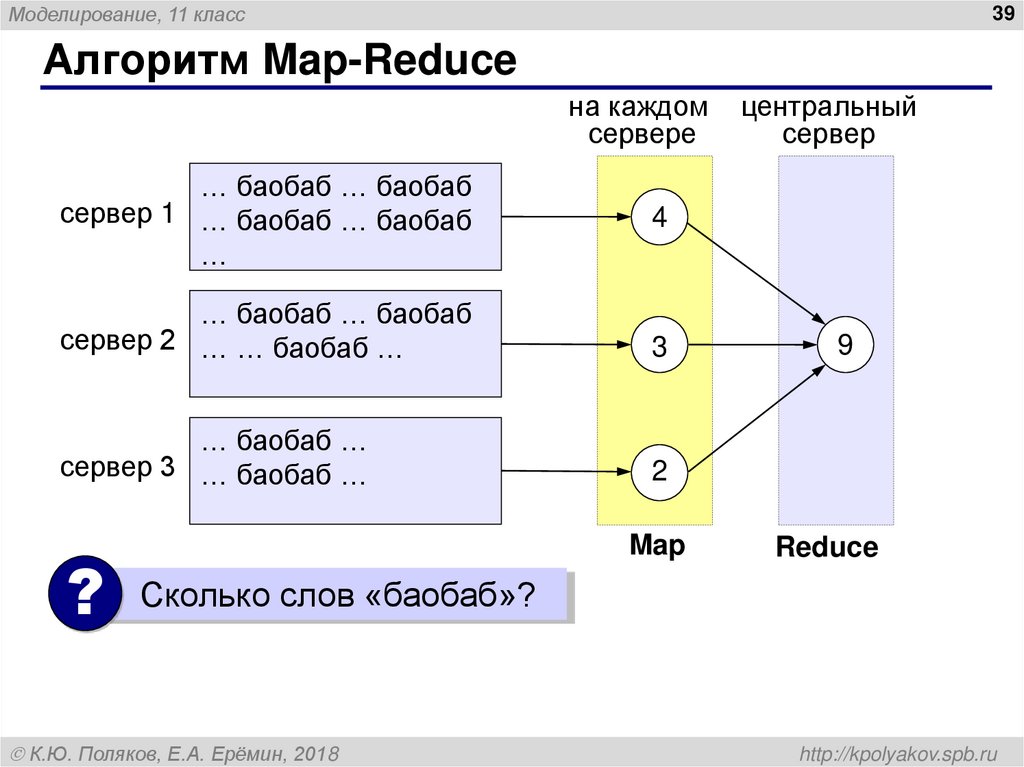
Алгоритм Map-Reduce
на каждом
сервере
… баобаб … баобаб
сервер 1 … баобаб … баобаб
…
4
… баобаб … баобаб
сервер 2 … … баобаб …
3
… баобаб …
сервер 3 … баобаб …
2
? Сколько слов «баобаб»?
К.Ю. Поляков, Е.А. Ерёмин, 2018
центральный
сервер
Map
9
Reduce
http://kpolyakov.spb.ru
40. Моделирование
40Моделирование
§ 9. Этапы моделирования
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
41. I. Постановка задачи
Моделирование, 11 класс41
I. Постановка задачи
• исследование оригинала
изучение сущности объекта или явления
• анализ («что будет, если …»)
научиться прогнозировать последствий при различных
воздействиях на оригинал
• синтез («как сделать, чтобы …»)
научиться управлять оригиналом, оказывая на него
воздействия
• оптимизация («как сделать лучше»)
выбор наилучшего решения в заданных условиях
!
Ошибки при постановке задачи приводят к
наиболее тяжелым последствиям!
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
42. I. Постановка задачи
Моделирование, 11 класс42
I. Постановка задачи
Хорошо поставленная задача:
• описаны все связи между исходными данными и
результатом
• известны все исходные данные
• решение существует
• задача имеет единственное решение
Примеры плохо поставленных задач:
• Уроки в школе начинаются в 830. В 1000 к школе подъехал
красный автомобиль. Определите, когда Вася выйдет
играть в футбол?
• Вася бросает мяч со скоростью 12 м/с. Где мяч впервые
ударится о землю?
• Решить уравнение sin x = 4 (нет решений).
• Найти функцию, которая проходит через точки (0,1) и (1,0)
(бесконечно много решений).
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
43. I. Постановка задачи (пример)
Моделирование, 11 класс43
I. Постановка задачи (пример)
Спортсмен Вася в синей кепке бросает белый мяч со
скоростью 12 м/с. Под каким углом к горизонту ему нужно
бросить мяч, чтобы попасть в желтую мишень?
? Хорошо поставлена?
Допущения:
Мишень расположена на высоте 4 м на расстоянии 10
м от Васи. В момент броска мяч находится на высоте
2 м от земли.
? Всегда ли есть решение?
? Решение единственно?
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
44. II. Разработка модели
Моделирование, 11 класс44
II. Разработка модели
Спортсмен Вася в синей кепке бросает белый мяч со
скоростью 12 м/с. Под каким углом к горизонту ему нужно
бросить мяч, чтобы попасть в желтую мишень? Мишень
расположена на высоте 4 м на расстоянии 10 м от Васи.
В момент броска мяч находится на высоте 2 м от земли.
1) Определить существенные исходные данные.
• мяч и мишень — материальные точки
• мишень неподвижна
• сопротивление воздуха не учитывается.
2) Выбор типа модели.
!
Можно использовать несколько моделей!
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
45. II. Разработка модели
,Моделирование, 11 класс45
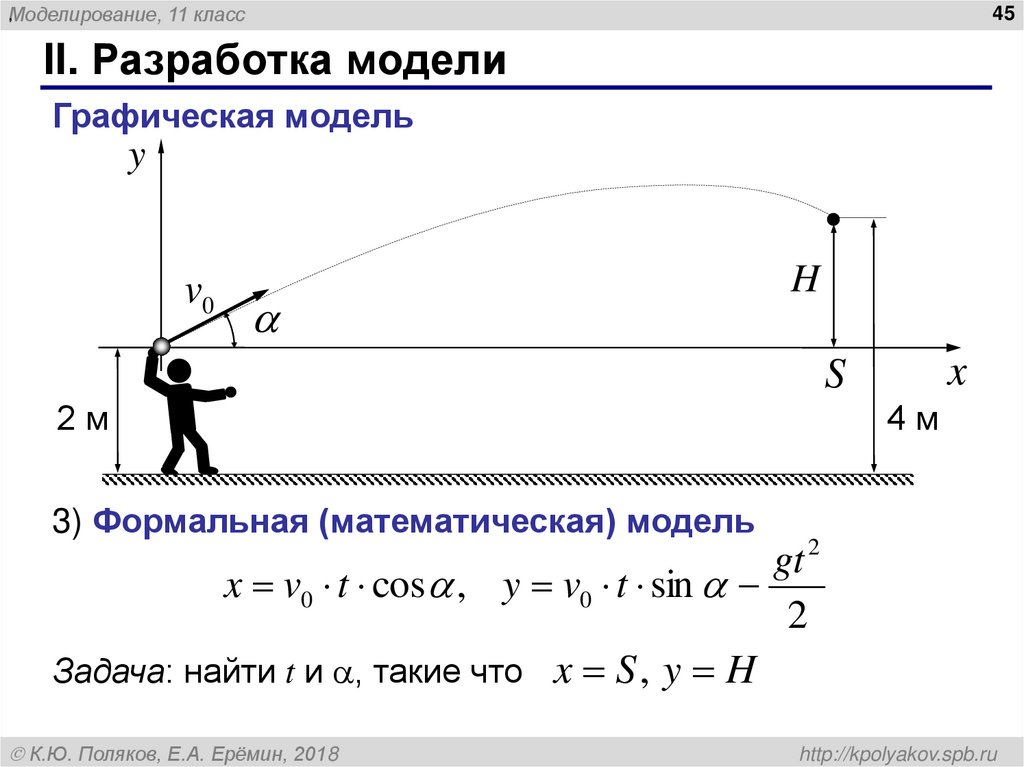
II. Разработка модели
Графическая модель
y
v0
H
x
S
2м
4м
3) Формальная (математическая) модель
gt 2
x v0 t cos , y v0 t sin
2
Задача: найти t и , такие что x S , y H
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
46. Уточнение диапазона углов
Моделирование, 11 класс46
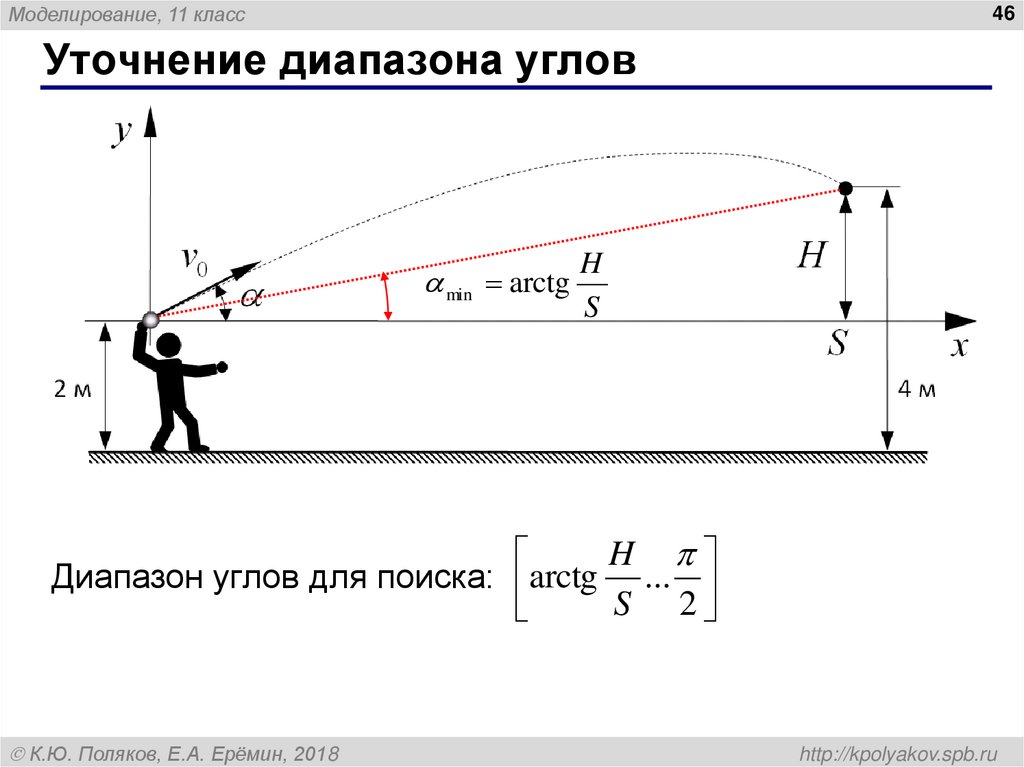
Уточнение диапазона углов
min arctg
H
S
H
Диапазон углов для поиска: arctg ...
S 2
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
47. II. Разработка модели
Моделирование, 11 класс47
II. Разработка модели
4) Алгоритм моделирования
Метод I.
Меняем угол . Для выбранного угла строим
траекторию полета мяча. Если она проходит выше
мишени, уменьшаем угол, если ниже – увеличиваем.
Метод II.
Из первого равенства выражаем время полета:
v0 cos t S
S
t
v0 cos
Меняем угол . Для выбранного угла считаем t, а
затем – значение y при этом t. Если оно больше H,
уменьшаем угол, если меньше – увеличиваем.
не надо строить всю траекторию для каждого
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
48. II. Разработка модели
Моделирование, 11 класс48
II. Разработка модели
5) Компьютерная модель
• программа (Паскаль, Си, …)
• электронные таблицы (Excel, OpenOffice.org Calc)
• среды моделирования (Simulink, VisSim)
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
49. III. Тестирование модели
Моделирование, 11 класс49
III. Тестирование модели
Тестирование – это проверка модели на простых
исходных данных с известным результатом.
а) тестирование математической модели:
gt
x v0 t cos , y v0 t sin
2
2
• при t = 0 x = 0, y = 0 (в начале координат)
gt 2
• при v0 = 0 x = 0, y
(падение вниз)
2
• при = 90 x = 0
• при увеличении t парабола «загибается» вниз
б) тестирование компьютерной модели:
(пробные расчёты в рассмотренных условиях)
? Доказывает ли успешное тестирование
правильность модели?
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
50. IV. Эксперимент с моделью
Моделирование, 11 класс50
IV. Эксперимент с моделью
Эксперимент – это исследование модели при тех
исходных данных, которые нас интересуют (результат
заранее неизвестен).
1) задаём угол
S
2) находим время t
v0 cos
3) находим высоту
gt 2
t cos , y v0 t sin
2
! Может быть два
решения!
y<H
H
Диапазон углов для поиска: arctg ...
S 2
? Можно ли сразу использовать двоичный поиск?
? Как отделить два решения? построить график y( )
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
51. V. Анализ результатов эксперимента
Моделирование, 11 класс51
V. Анализ результатов эксперимента
! Необходима проверка на оригинале!
Возможные выводы:
• задача решена, модель адекватна
• необходимо изменить алгоритм или условия
моделирования
• необходимо изменить модель (учесть
дополнительные свойства)
• необходимо изменить постановку задачи
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
52. V. Анализ результатов
Моделирование, 11 класс52
V. Анализ результатов
• всегда ли Вася сможет попасть в мишень?
• если начальная скорость отличается от заданной?
• если мяч и мишень не считать материальными
точками?
• как сильно влияет сопротивление воздуха?
• если мишень качается?
• и т.д….
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
53. Моделирование
53Моделирование
§ 10. Моделирование движения
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
54. Задача
Моделирование, 11 класс54
Задача
y
hmax
вверх
v
F
G
вниз
• найти hmax
• найти v при приземлении
v
? Какой тип движения?
F
G
0
равномерное?
равноускоренное?
x
? Какая ещё сила?
G m g
не меняется!
плотность воздуха
F
v2
2
C S площадь
сечения
шар: С = 0,4
К.Ю. Поляков, Е.А. Ерёмин, 2018
1,23 кг/м3
S r2
http://kpolyakov.spb.ru
55. Математическая модель
Моделирование, 11 класс55
Математическая модель
В проекции на ось OY:
G m g
F
G F
a
m
v v
2
всегда противоположна v
C S
! Силы меняются ускорение меняется!
Методы решения:
•аналитический (высшая математика)
•численное моделирование
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
56. Дискретизация
Моделирование, 11 класс56
Дискретизация
Дискретная модель описывает состояние системы при
t 0, , 2 , 3 , ...
шаг дискретизации
Задача: зная (yi, vi, ai) при ti = i
найти (yi+1, vi+1, ai+1) при ti+1 = (i+1)
Допущение: силы (и ускорение) не меняются
на интервале [ti, ti+1]
Вычисления:
Fi
vi vi
2
C S
vi 1 vi ai
К.Ю. Поляков, Е.А. Ерёмин, 2018
G Fi
Fi
ai
g
m
m
ai 2
yi 1 yi vi
2
http://kpolyakov.spb.ru
57. Компьютерная модель
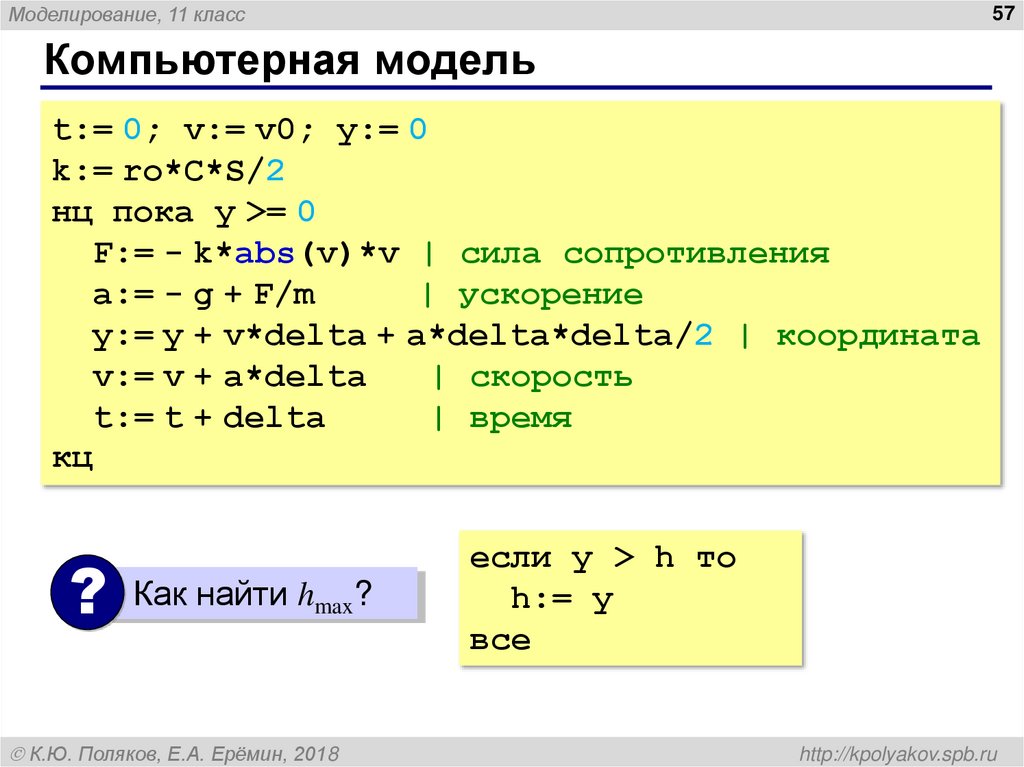
Моделирование, 11 класс57
Компьютерная модель
t:= 0; v:= v0; y:= 0
k:= ro*C*S/2
нц пока y >= 0
F:= - k*abs(v)*v | сила сопротивления
a:= - g + F/m
| ускорение
y:= y + v*delta + a*delta*delta/2 | координата
v:= v + a*delta
| скорость
t:= t + delta
| время
кц
? Как найти h ?
max
К.Ю. Поляков, Е.А. Ерёмин, 2018
если y > h то
h:= y
все
http://kpolyakov.spb.ru
58. Моделирование
58Моделирование
§ 11. Математические модели
в биологии
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
59. Модель неограниченного роста (Т. Мальтус)
Моделирование, 11 класс59
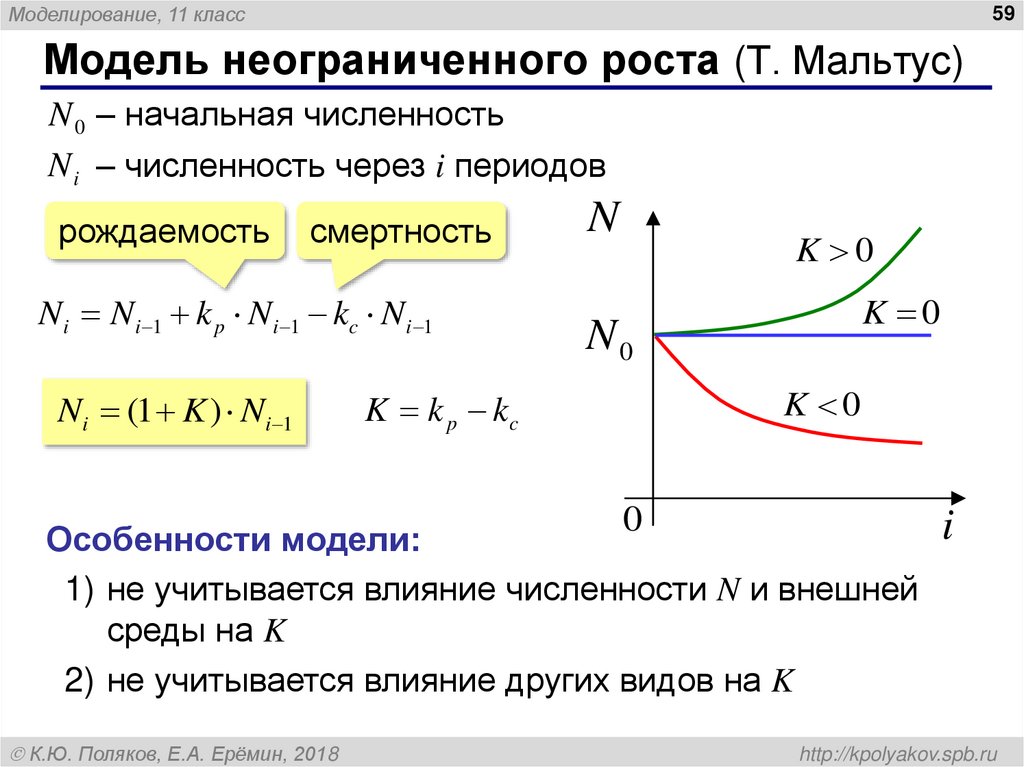
Модель неограниченного роста (Т. Мальтус)
N 0 – начальная численность
N i – численность через i периодов
рождаемость
смертность
Ni Ni 1 k p N i 1 kc N i 1
Ni (1 K ) Ni 1
N
K 0
K 0
N0
K 0
K k p kc
0
i
Особенности модели:
1) не учитывается влияние численности N и внешней
среды на K
2) не учитывается влияние других видов на K
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
60. Модель ограниченного роста (П. Ферхюльст)
Моделирование, 11 класс60
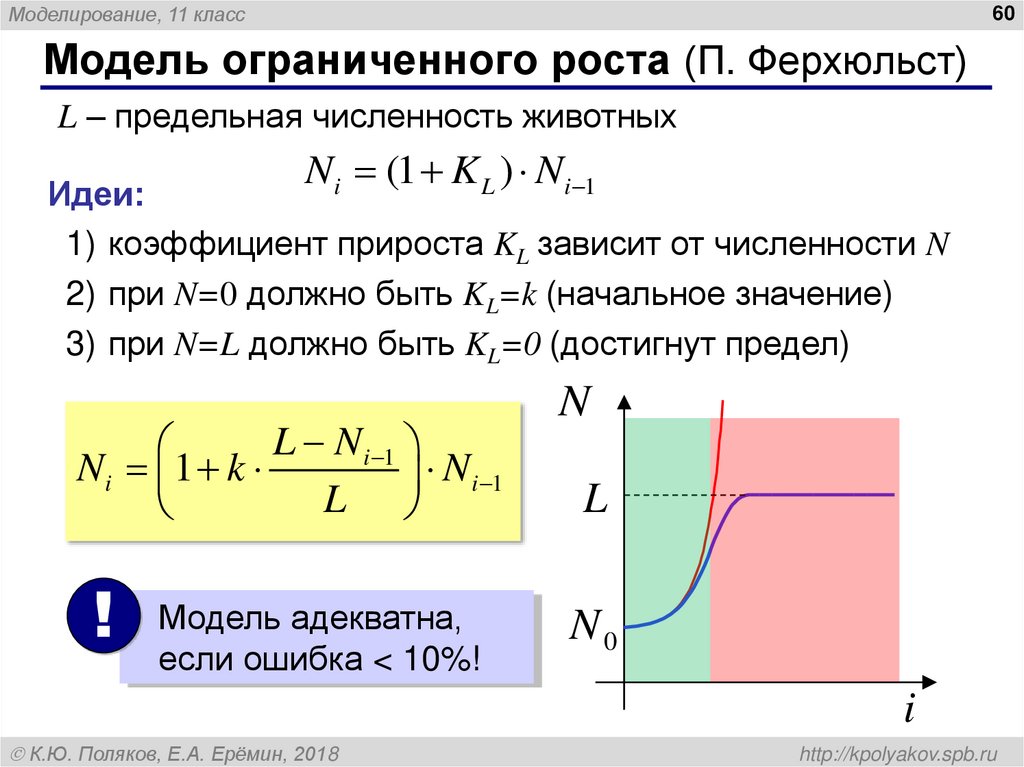
Модель ограниченного роста (П. Ферхюльст)
L – предельная численность животных
Ni (1 K L ) Ni 1
Идеи:
1) коэффициент прироста KL зависит от численности N
2) при N=0 должно быть KL=k (начальное значение)
3) при N=L должно быть KL=0 (достигнут предел)
L N i 1
Ni 1 k
N i 1
L
!
Модель адекватна,
если ошибка < 10%!
N
L
N0
i
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
61. Модель с отловом
Моделирование, 11 класс61
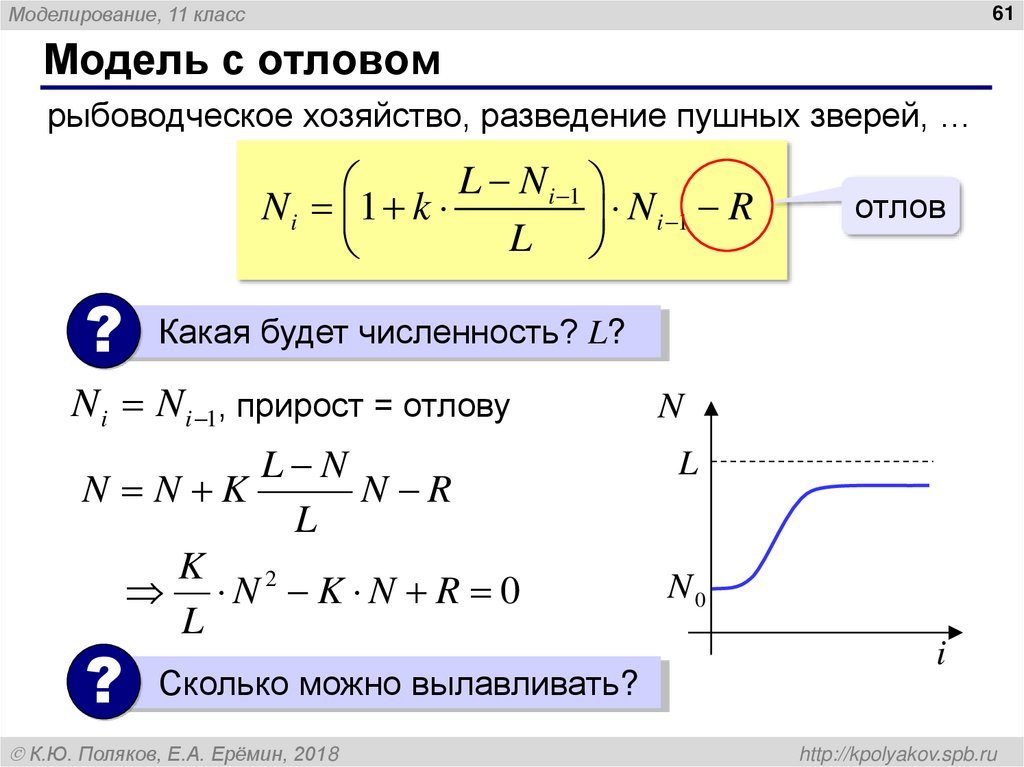
Модель с отловом
рыбоводческое хозяйство, разведение пушных зверей, …
L N i 1
Ni 1 k
N i 1 R
L
отлов
? Какая будет численность? L?
N i N i 1, прирост = отлову
N
L N
N N K
N R
L
K
N2 K N R 0
L
L
? Сколько можно вылавливать?
К.Ю. Поляков, Е.А. Ерёмин, 2018
N0
i
http://kpolyakov.spb.ru
62. Модель «хищник-жертва»
Моделирование, 11 класс62
Модель «хищник-жертва»
Модель – не-система:
щуки
караси
L N i 1
Ni 1 k
N i 1
L
Zi 1 D Zi 1
вымирают
без еды
Модель – система:
1) число встреч пропорционально Ni Zi
2) «эффект» пропорционален числу встреч
численность уменьшается
Ni (1 Ki 1 bN Z i 1 ) N i 1
Zi (1 D bZ Ni 1 ) Z i 1
численность увеличивается
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
63. Модель «хищник-жертва»
Моделирование, 11 класс63
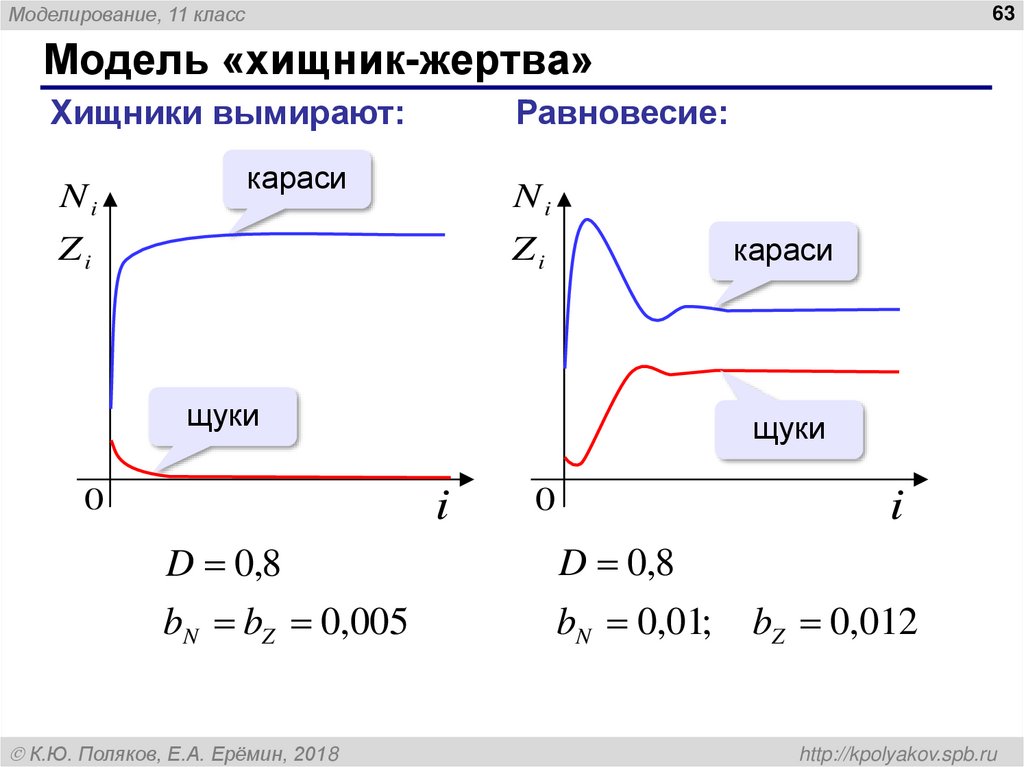
Модель «хищник-жертва»
Хищники вымирают:
Ni
Равновесие:
караси
Ni
Zi
караси
Zi
щуки
0
щуки
i
D 0,8
bN bZ 0,005
К.Ю. Поляков, Е.А. Ерёмин, 2018
0
i
D 0,8
bN 0,01;
bZ 0,012
http://kpolyakov.spb.ru
64. Модель «хищник-жертва»
Моделирование, 11 класс64
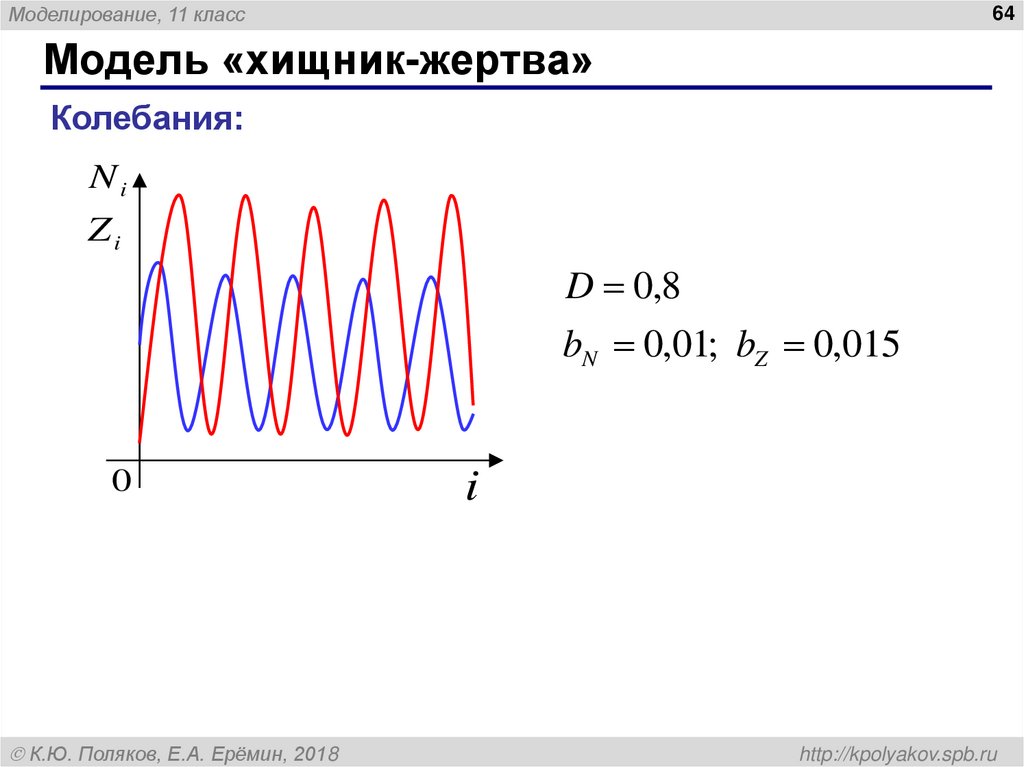
Модель «хищник-жертва»
Колебания:
Ni
Zi
D 0,8
bN 0,01; bZ 0,015
0
К.Ю. Поляков, Е.А. Ерёмин, 2018
i
http://kpolyakov.spb.ru
65. Обратная связь
Моделирование, 11 класс65
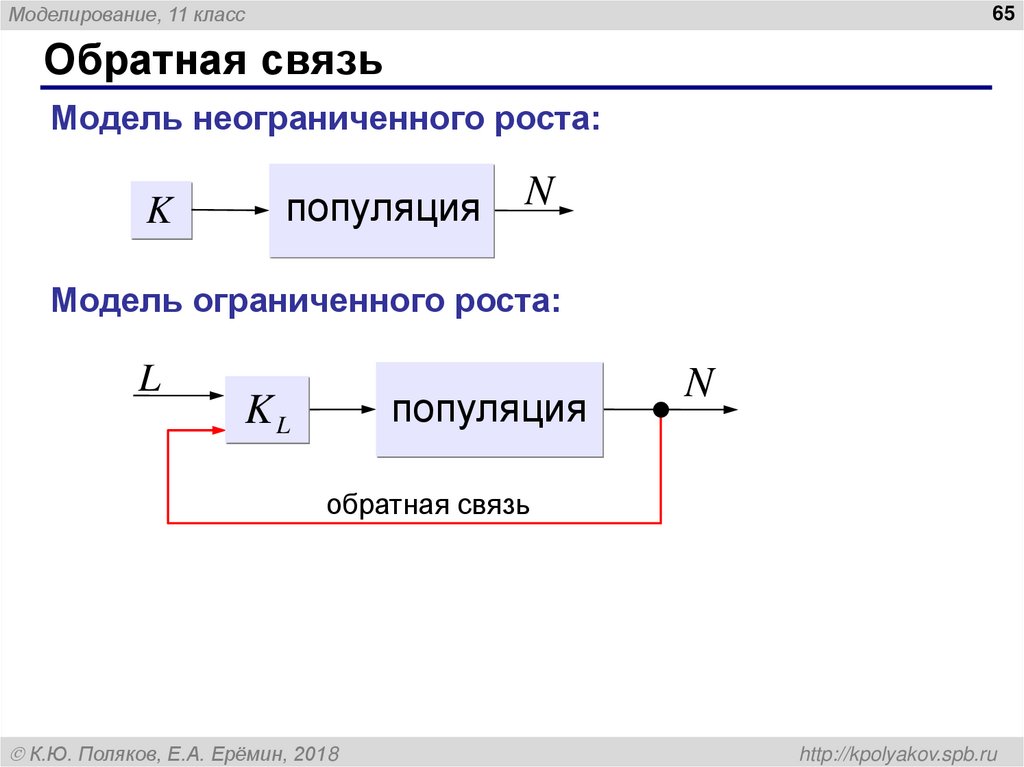
Обратная связь
Модель неограниченного роста:
K
популяция
N
Модель ограниченного роста:
L
популяция
KL
N
обратная связь
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
66. Саморегуляция
Моделирование, 11 класс66
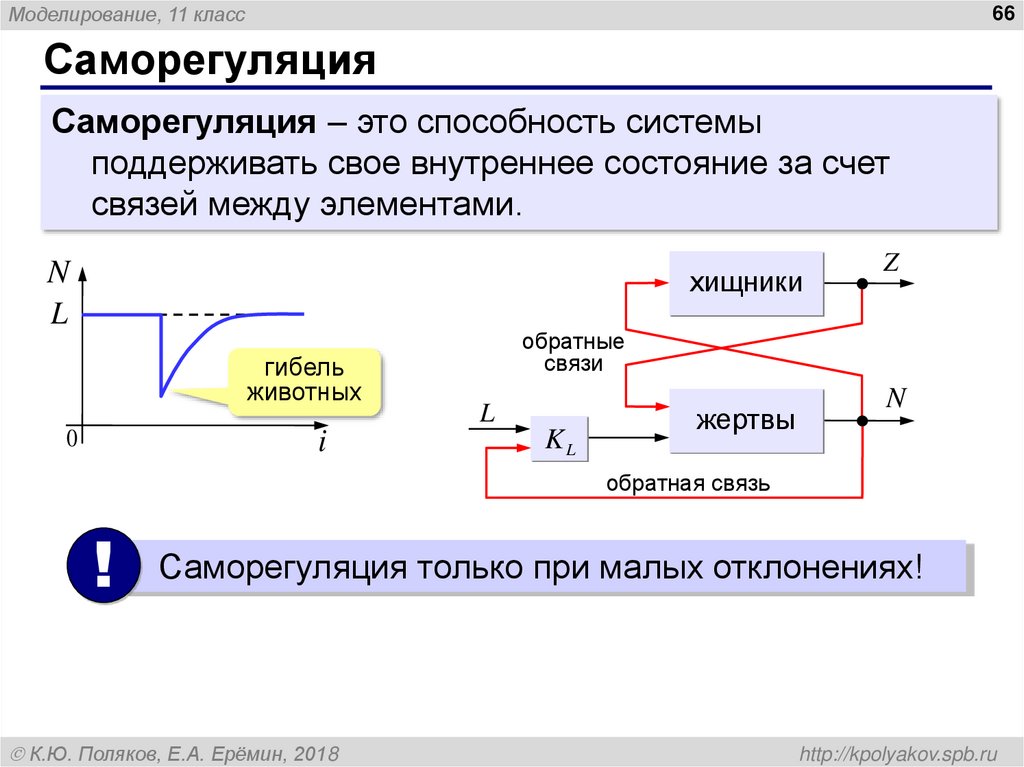
Саморегуляция
Саморегуляция – это способность системы
поддерживать свое внутреннее состояние за счет
связей между элементами.
N
L
хищники
гибель
животных
i
0
Z
обратные
связи
L
KL
жертвы
N
обратная связь
!
Саморегуляция только при малых отклонениях!
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
67. Моделирование
67Моделирование
§ 12. Вероятностные модели
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
68. Методы Монте-Карло
Моделирование, 11 класс68
Методы Монте-Карло
Методы Монте-Карло – это методы решения
вычислительных задач с помощью математического
моделирования, основанные на использовании
случайных чисел.
результат приближённый
это лучше, чем никакой
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
69. Вычисление площади
Моделирование, 11 класс69
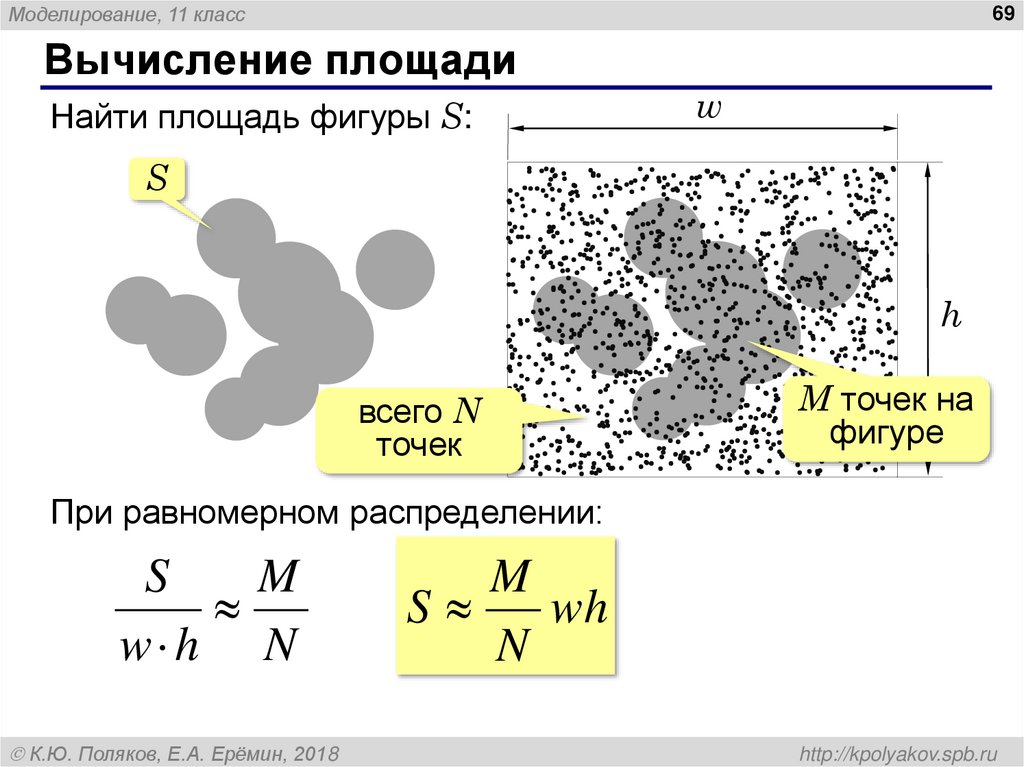
Вычисление площади
Найти площадь фигуры S:
w
S
h
всего N
точек
M точек на
фигуре
При равномерном распределении:
S
M
w h N
К.Ю. Поляков, Е.А. Ерёмин, 2018
M
S
wh
N
http://kpolyakov.spb.ru
70. Вычисление числа
Моделирование, 11 класс70
Вычисление числа
y
-1
0
S1
1 x
S R 2
если внутри
круга
R 2
4
4
M
M
4S1 4 1 4
N
N
цел i, M = 0, N = 100000
вещ x, y
нц для i от 1 до N
x := rand(0,1)
y := rand(0,1)
если x*x + y*y <= 1 то
M:= M + 1
все
кц
вывод "Pi = ", 4*M/N
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
71. Системы массового обслуживания (СМО)
Моделирование, 11 класс71
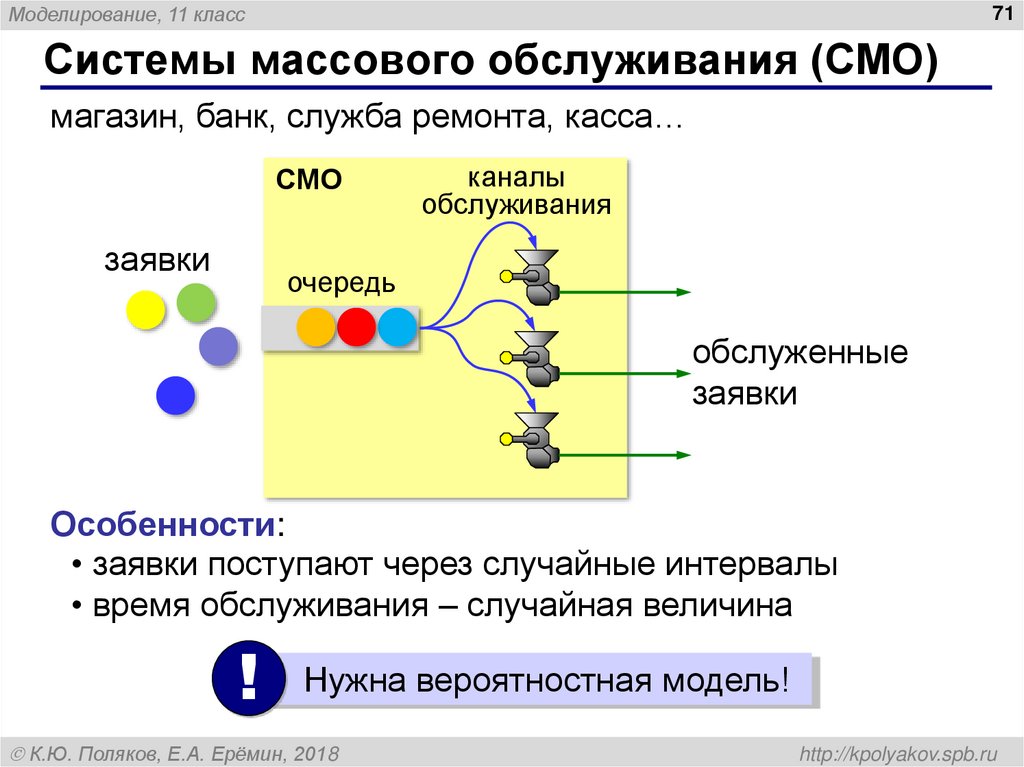
Системы массового обслуживания (СМО)
магазин, банк, служба ремонта, касса…
СМО
заявки
каналы
обслуживания
очередь
обслуженные
заявки
Особенности:
• заявки поступают через случайные интервалы
• время обслуживания – случайная величина
!
Нужна вероятностная модель!
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
72. Модель работы банка
Моделирование, 11 класс72
Модель работы банка
Детерминированная модель:
• за 1 минуту входит P клиентов
• время обслуживания T минут
? Сколько нужно
касс?
K P T
Допущение:
распределение
равномерное
Вероятностная модель:
• K – количество касс
• за 1 минуту входит от 0 до Pmax клиентов
• время обслуживания от Tmin до Tmax минут
• изменение числа клиентов в банке
Ni 1 Ni Pi Ri
вошли за i-ую минуту
обслужены за
i-ую минуту
Ni
• средняя длина очереди Qi
K
• среднее время ожидания Qi Ti
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
73. Модель работы банка
Моделирование, 11 класс73
Модель работы банка
? Как найти R ?
i
Допущение:
K касс работают с одинаковой скоростью, но эта
скорость меняется каждый интервал
Ti – случайное время обслуживания (от Tmin до Tmax)
обслужено за 1 интервал на 1 кассе 1/T,
на всех кассах
K
Ri
Ti
Задача: выбрать K так, чтобы среднее время ожидания
было больше допустимого в течение не более 5% от
полного времени моделирования.
Ni
допустимое
«плохие минуты»: Qi Ti
Ti M
время ожидания
K
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
74. Модель работы банка
Моделирование, 11 класс74
Модель работы банка
K:= 2
| меняем количество касс
Pmax:= 4 | макс. число входящих за 1 мин
Tmin:= 1 | мин. время обслуживания
Tmax:= 9 | макс. время обслуживания
L:= 480
| период моделирования
M:= 15
| допустимое время ожидания
N:= 0
| сначала в банке никого нет
count:= 0 | счетчик «плохих» минут
? Что выводить в результате?
count
0,05 касс достаточно
L
! Сравнить с детерминированной моделью!
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
75. Модель работы банка (КуМир)
Моделирование, 11 класс75
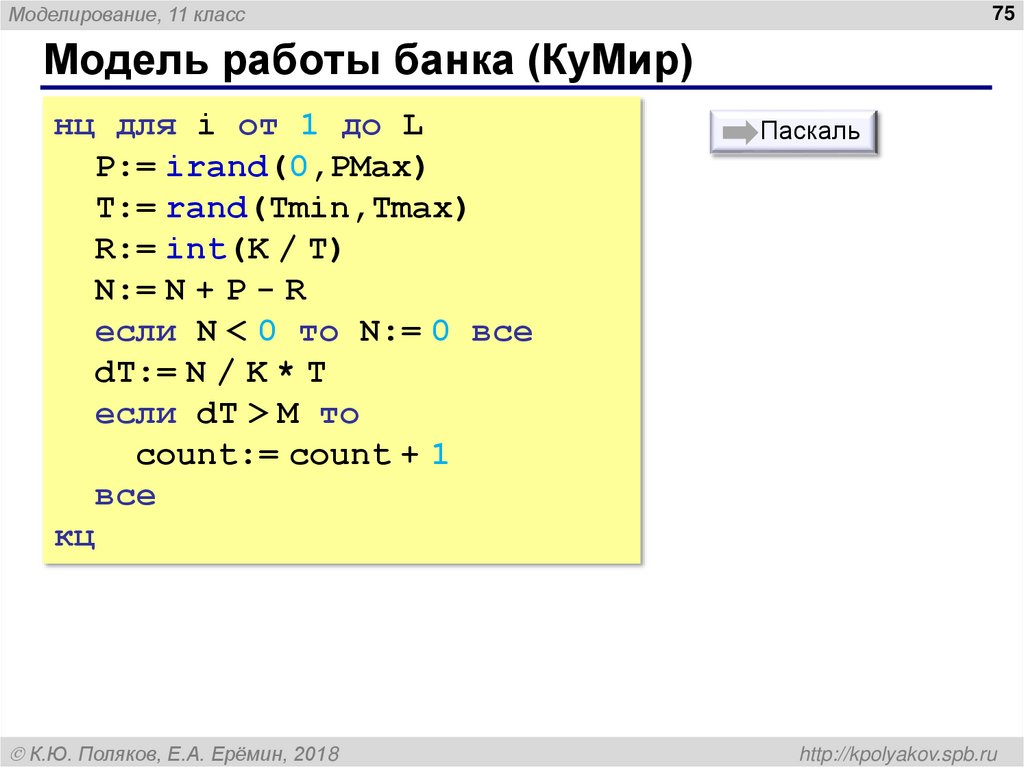
Модель работы банка (КуМир)
нц для i от 1 до L
P:= irand(0,PMax)
T:= rand(Tmin,Tmax)
R:= int(K / T)
N:= N + P - R
если N < 0 то N:= 0 все
dT:= N / K * T
если dT > M то
count:= count + 1
все
кц
К.Ю. Поляков, Е.А. Ерёмин, 2018
Паскаль
http://kpolyakov.spb.ru
76. Модель работы банка (Паскаль)
Моделирование, 11 класс76
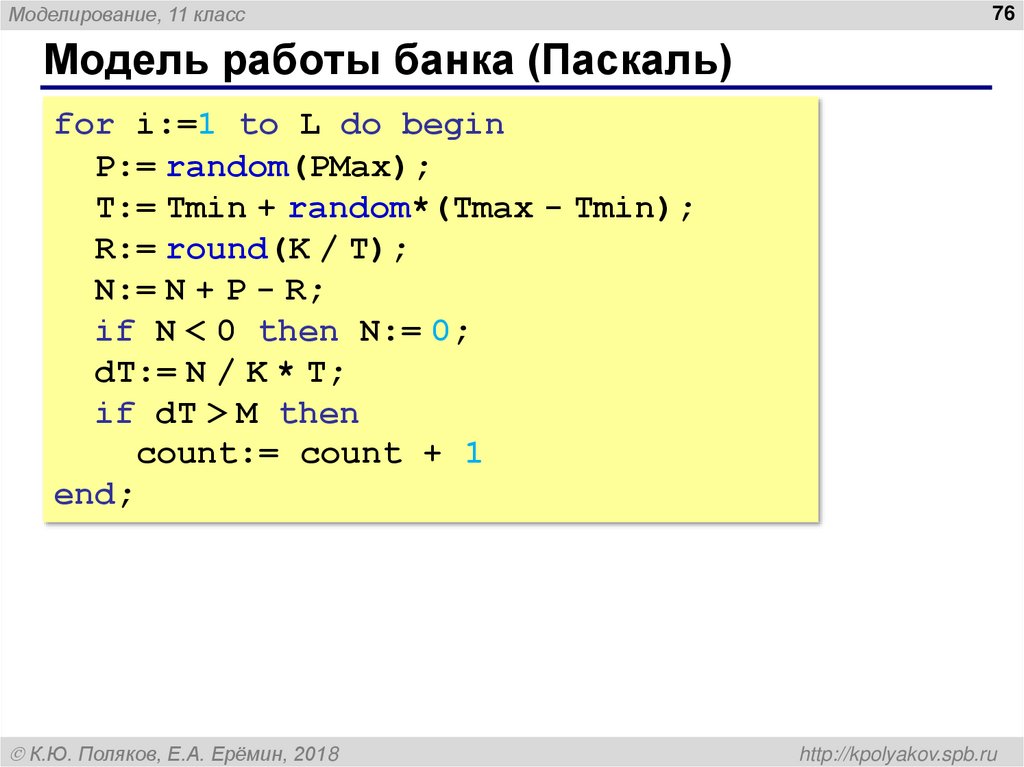
Модель работы банка (Паскаль)
for i:=1 to L do begin
P:= random(PMax);
T:= Tmin + random*(Tmax - Tmin);
R:= round(K / T);
N:= N + P - R;
if N < 0 then N:= 0;
dT:= N / K * T;
if dT > M then
count:= count + 1
end;
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
77. Уточнение модели
Моделирование, 11 класс77
Уточнение модели
• за 1 минуту входит от 0 до Pmax клиентов
Допущение: распределение
Распределение Пуассона:
равномерное
P
вероятность
того, что P = k
5
p(k )
0
5
10
Pсреднее
k
k!
e
15
Получение из равномерного распределения:
метод обратных функций
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
78. Распределение Пуассона (КуМир)
Моделирование, 11 класс78
Распределение Пуассона (КуМир)
алг цел Poisson(цел Lam)
нач
вещ s, r, alpha;
цел k
r:= exp(-Lam); s:= r
k:= 0
alpha:= rand(0,1)
нц пока s < alpha
k:= k + 1
r:= r * Lam / k
s:= s + r
кц
знач:= k
кон
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
79. Распределение Пуассона (Паскаль)
Моделирование, 11 класс79
Распределение Пуассона (Паскаль)
function Poisson(Lam: integer): integer;
var s, r, alpha: real;
k: integer;
begin
r:= exp(-Lam); s:= r;
k:= 0;
alpha:= random;
while s < alpha do begin
k:= k + 1;
r:= r * Lam / k;
s:= s + r
end;
Poisson:= k
end;
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
80. Конец фильма
Моделирование, 11 класс80
Конец фильма
ПОЛЯКОВ Константин Юрьевич
д.т.н., учитель информатики
ГБОУ СОШ № 163, г. Санкт-Петербург
kpolyakov@mail.ru
ЕРЕМИН Евгений Александрович
к.ф.-м.н., доцент кафедры мультимедийной
дидактики и ИТО ПГГПУ, г. Пермь
eremin@pspu.ac.ru
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
81. Источники иллюстраций
Моделирование, 11 класс81
Источники иллюстраций
1. www.historicships.com
2. www.amazon.co.uk
3. www.supahcars.com
4. physicon.ru
5. www.laerdal.com
6. biohimija.ru
7. ecosafe.spbu.ru
8. www.skyplaz.ru
9. www.burpipe.ru
10. www.garshin.ru
11. www.thisnext.com
12. 3dsdesign.ru
13. en.wikipedia.org
14. ru.wikipedia.org
15. www.m24.ru
16. naked-science.ru
17. medium.com
18. иллюстрации художников издательства «Бином»
19. авторские материалы
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
















































 Информатика
Информатика








