Похожие презентации:
Представление информации в ЭВМ
1.
ИНФОРМАТИКАлекция
Представление информации в ЭВМ
1
2.
Структура памятиАдреса байтов
0
1
2
…….
3
Память
N
…..
Номера
битов байте
Байты
7
Байт
6
5
4
3
0
2
1
0
1
Биты
Один байт состоит из восьми бит
2
3.
Машинное словоПоследовательность битов и байтов рассматриваемых
аппаратной частью ЭВМ как одно целое.
1 байт
Длина машинного слова:
2 байта
4 байта … ….
A1
A2
A2+1
A3
A3+1
A3+2
A3+3
Байт определяющий адрес машинного слова
3
4.
Объем (емкость) памятиОбъем памяти – наибольший объем данных, которые
одновременно могут храниться в запоминающем устройстве.
Единицы измерения объема памяти:
1 бит.
1 байт = 8 бит.
1 Кбайт (кило) = 1024
байт = 210 байт, 1 кбайт =103 байт.
1 Мбайт (мега) = 1024 Кбайт = 220 байт, 1 мбайт =106 байт.
1 Гбайт (гига) = 1024 Мбайт = 230 байт, 1 гбайт =109 байт.
1 Тбайт (тера) = 1024 Гбайт = 240 байт, 1 тбайт =1012 байт.
1 Пбайт (пета) = 1024 Tбайт = 250 байт ,1 пбайт =1015 байт.
4
5.
Виды информацииСимвольная и текстовая
Графическая
Числовая
Звуковая
Видио
5
6.
Формат хранения целых неотрицательныхдвоичных чисел с фиксированной точкой без
знака
Первый байт числа
Второй байт числа
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
Символ b обозначает двоичную цифру: 0 или 1.
Целое число над этим символом номер ее разряда.
Цифры с номерами разрядов от 0 до 7 образуют второй байт.
Цифры с номерами разрядов от 8 до 15— первый байт числа. 6
7.
Пример формата хранения числа 25810Второй байт числа
Первый байт числа
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
7
8.
Максимальное число форматаМаксимальное целое неотрицательное число L определяется
размером слова l в байтах, используемого для хранения
числа:
L = 28 l 1,
где L максимальное целое неотрицательное число;
l размер слова в байтах, необходимых для хранения
числа.
8
9.
Значение максимального числаРазмер слова в
байтах
Размер слова в
битах
Значение
максимального
числа
1
8
28 -1= 255
2
16
216 1 = 65535
4
32
232 1 =
=4294967295
8
64
264 1 > 16 1018
9
10.
Определение минимального размера словаНайдем минимальную длину слова в байтах lmin,
необходимого для хранения целого неотрицательного
числа L:
log2(L+1) = 8 l;
l =log2(L+1) / 8.
Размер слова lmin выбирается из множества допустимых
значений: 1, 2, 4, 8. Размер слова lmin должен быть
минимальным, но не меньше l.
10
11.
Пример решения задачиПоказать структуру хранения в памяти числа 50510.
Использовать слово с наименьшим размером.
Переведем число 50510в двоичную систему счисления.
В результате перевода получим двоичное число:
50510 = 1111110012.
Минимальная количество байтов, необходимых для записи
числа в память равна:
l = log2(L+1) / 8 = log2(505+1) / 8 = log2 506 /8 ( байт ).
11
12.
Продолжение решения примераОчевидно:
log2 256 < log2 506 < log2 512
log228 < log2 506 < log229
8< log2 506 < 9
Откуда получаем:
1< log2 506/8 < 9/8
1< log2 506/8 < 2
Первый байт числа
Второй байт числа
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
0
0
0
0
0
0
0
1
1
1
1
1
1
0
0
1
12
13.
Представление целых отрицательных чисел в ЭВМФормат хранения целых чисел со знаком аналогичен
формату хранения двоичного числа без знака, за исключением
того, что старший разряд числа отводится для хранения знака
числа: s.
При хранении положительного числа знаковый разряд
принимает значение 0, а при хранении . отрицательного числа
равен 1.
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
s
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
Целое число со знаком может занимать в памяти один, два, четыре
и восемь байтов.
13
14.
Дополнительный код числаДля хранения отрицательных целых чисел используется
дополнительный код числа.
Правило № 6.
Чтобы найти представление m разрядного двоичного целого
отрицательного числа в дополнительном коде с количеством
двоичных разрядов n (n>m) необходимо выполнить следующие
действия:
1.1. Дополнить число слева n-m нулями до разрядности n.
2.2. Найти обратный код полученного числа. При этом двоичные
нули исходного числа заменяются двоичными единицами, а
двоичные единицы двоичными нулями.
3.3. К полученному обратному коду прибавить единицу.
14
15.
Пример нахождения дополнительного кодачисла
Найдем шестиразрядный дополнительный код числа 1002.
1.Дополним исходное число до необходимой разрядности:
100 000100.
2. Найдем обратный код полученного числа:
000100
111011
3. Прибавим единицу к полученному коду:
111011 + 1 =111100.
15
16.
Дополнительный код чисел вида: -2n-1Заметим, что отрицательные целые n разрядные числа вида:
2n 1 можно записать в дополнительном коде с n разрядами.
Пример Найдем 6 разрядный дополнительный код 6 разрядного
числа 25:
1.
Дополнять исходное число 25 = 1000002 до разрядности
равной 6 в этом случае нет необходимости. Число 25 уже
шестиразрядное.
2. Найдем значения обратного кода:
100000
011111
3. Прибавим единицу к полученному числу:
011111 + 1 =100000.
Таким образом, дополнительный код числа 25 равен 100000.
16
17.
Получение прямого кода числа по его дополнительному кодуПравило № 7.
Чтобы записать прямой код отрицательного числа,
представленного в n разрядном дополнительном коде,
необходимо:
1. Найти обратный код полученного числа. Для этого
необходимо заменить в разрядах di (i=0, n 1) нули единицами,
а единицы нулями.
2. К полученному числу прибавить единицу. При этом
будет получена абсолютная величина искомого отрицательного
числа в двоичной системе счисления.
3. Слева приписать к полученной абсолютной величине
знак минус.
17
18.
Пример восстановления прямого кода числа (проверкапредыдущего примера)
1
Найдем обратный код дополнительного кода числа:
100000
011111
2
К полученному числу прибавим единицу:
0111112 + 12 = 1000002.
3
Слева к полученному числу припишем знак минус:
1000002 1000002.
Полученный результат совпал с исходным числом:
1000002 = 25.
18
19.
Минимальные и максимальные значения чиселЗначения минимальных отрицательных и максимальных
положительных целых чисел, которые можно хранить в словах
размера 1, 2,4 и 8 байтов, показаны в таблице. При заполнении
таблицы использовались выражения для определения минимального
отрицательного и максимального положительного числа:
Lmin = 28 l 1,
Lmax = 28 l 1 1,
где Lmin минимальное целое отрицательное число,
представленное в дополнительном коде;
Lmax максимальное целое положительное число,
представленное в прямом коде;
l размер слова в байтах.
19
20.
Значения минимальных и максимальных чиселРазмер
слова в
байтах
Размер слова
в битах
Значение
минимального числа
Значение
максимального числа
1
8
(27 )= 128
(27 1)= 127
2
16
(215 ) = 32768
(215 1) =32767
4
32
(231 ) = 2147483648
(231 1) =2147483647
8
64
(263 ) < 16 1018
(263 1) >16 1018
20
21.
Представление дробных чисел в ЭВМЗ
н
Порядок
1 байт
Мантисса
2 байт
3 байт
4 байт
7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0
З b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b b
н
21
22.
Представление десятичного дробного числа в короткомформате
Этапы:
1. Перевод числа в двоичную систему счисления
2. Округление числа
3. Нормализация числа
4. Получение смещенного порядка
5. Запись числа в память
22
23.
1. Перевод числа в двоичную систему счисления.Определение точности перевода неправильной дроби
Если число по абсолютной величине больше или равно единице,
то количество дробных разрядов (точность перевода) числа
можно определить следующим образом:
m + n + 1 = 25; m = 24 – n,
где n номер старшего разряда числа, m количество разрядов
дробной части искомого числа.
Искомое число должно содержать 25 значащих разрядов.
23
24.
Определение точности перевода правильной дробиЕсли число по абсолютной величине меньше единицы, то при
переводе правильной десятичной дроби необходимо определить
номер первого разряда дробной части искомого двоичного числа, в
котором будет располагаться двоичная единица.
Пусть номер найденного разряда –j. Обозначим через l
количество разрядов с двоичными нулями, расположенными между
разделительной точкой и разрядом с номером –j, l = j – 1. Тогда
точность перевода равна:
m = l + 25.
Разряды с номерами небольшими, чем –j назовем значащими
разрядами числа. Их количество должно быть равно 25.
24
25.
2. Округление числа.К полученному на первом шаге числу прибавляется
единица, по весу равная единице младшего разряда.
Затем младший разряд суммы отбрасывается.
В результате будет полученное число, содержащее 24
значащих разрядов.
25
26.
3. Нормализация числаДля этого необходимо перемещать разделительную
точку таким образом, чтобы искомое число,
полученное в результате перемещения точки,
располагалось на полусегменте [1, 2) (x - искомое
число, 1<= x 2).
Первоначально
абсолютный
принимается равный нулю.
порядок
числа
Если число оказывается больше или равно двух,
то разделительная точка перемещается влево.
При этом значение порядка увеличивается
на величину равную количеству разрядов, на которые
26
переместилась точка.
27.
3. Нормализация числаЕсли
исходное
число
меньше
то разделительная точка перемещается вправо.
единицы,
При этом значение порядка уменьшается на величину,
равную количеству разрядов, на которое переместилась
разделительная точка.
Полученный порядок числа называется абсолютным
порядком числа.
Целая часть числа, расположенного на полусегменте [1, 2),
равна единице.
Поэтому при хранении числа в памяти нет необходимости
в хранении целой части числа. Целая часть отбрасывается.
В этом случае остается мантисса (дробная часть числа),
содержащая 23 значащих разрядов.
27
28.
4. Определение смещенного порядка числа. Для этого необходимо к абсолютному порядку,
полученному на шаге 3 прибавить 127 (сместить порядок
на 127). В результате получим смещенный порядок числа.
Полученное десятичное число необходимо перевести в
двоичную систему счисления и представить в форме
8- разрядного целого неотрицательного двоичного числа
с фиксированной точкой без знака.
Смещенный
порядок
–
неотрицательное
число.
Максимальное значение абсолютного порядка равно: 128.
28
29.
5. Запись числа в памятьДробное число в коротком формате представляется в
памяти в форме нормализованного числа, занимающего
4 байта.
Старший бит первого байта (бит с номером 7) является
знаковым битом. Если число неотрицательное, то знак
числа равен нулю. Если число отрицательное, то знак
числа равен единице.
Смещенный порядок числа занимает 8 бит (1 байт) и
расположен с нулевого по 6-ой бит первого байта и в 7-ом
бите второго байта.
Мантисса числа занимает 23 бита и располагается во
втором байте с нулевого по 6-ой бит и полностью
29
занимает второй и третий байты числа.
30.
Представим дробное число 43.13 в коротком форматехранения
Переведем число 43.13 из десятичной системы счисления в двоичную
систему счисления.
Переводим целую часть числа:
43 : 2 = 21 (1), 21 ≥ 2
21 : 2 = 10 (1), 10 ≥ 2
10 : 2 = 5 (0), 5 ≥ 2
5 : 2 = 2 (1), 2 ≥ 2
2 : 2 = 1 (0), 1 ≤ 2
Целая часть равна: 4310 = 1010112.
n = 5.
30
31.
Перевод дробной части числа.Количество дробных разрядов числа определяем по
формуле m = 24 – n, где m – количество дробных разрядов
числа, n – номер старшего разряда целой части числа
m = 24 – 5 = 19.
Дробная часть равна: 0.1310 ≈ 0.00100001010001111012
Таким образом, 43.1310 ≈ 101011.00100001010001111012 .
31
32.
ОкруглениеК полученному числу прибавим двоичную единицу,
по весу равную единице младшего разряда:
101011.0010000101000111101
+
0.0000000000000000001
101011.0010000101000111110
Отбросим младший разряд суммы
В результате будет получено число:
равный
нулю.
101011.0010000101000111112
32
33.
Нормализация числаНормализуем число, перемещаем точку на пять разрядов
вправо:
101011.0010000101000111112 =
1.010110010000101000111112 2510
Отбросим старший разряд:
1.010110010000101000111112
0.010110010000101000111112
33
34.
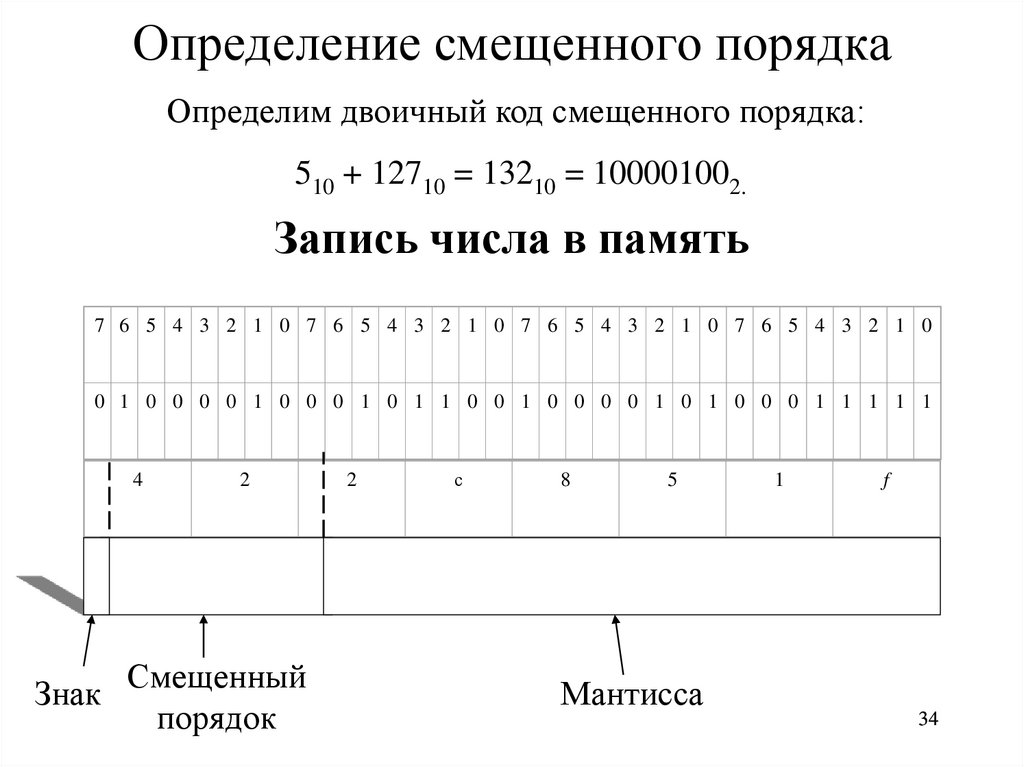
Определение смещенного порядкаОпределим двоичный код смещенного порядка:
510 + 12710 = 13210 = 100001002.
Запись числа в память
7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0
0 1 0 0 0 0 1 0 0 0 1 0 1 1 0 0 1 0 0 0 0 1 0 1 0 0 0 1 1 1 1 1
4
2
Знак Смещенный
порядок
2
с
8
5
Мантисса
1
f
34
35.
Представление символьной информацииСимвольная информация представляет собой набор
букв, цифр, знаков препинания, математических и
других символов. Совокупность всех символов,
используемых в ЭВМ, представляет ее алфавит.
Каждому символу соответствует свой код. Код
символа в памяти ЭВМ хранится в виде двоичного
числа.
35
36.
Способы кодирования символьной информацииКодирование символов с помощью
8разрядных кодов (байтов) (код ASCII - Американский
стандартный код для обмена информацией).
1.
С помощью байта можно закодировать 256 различных
символов.
2. В 1988 году компаниями Apple и Xerox был разработан
Unicode стандарт на двух байтовые символы.
Unicode код позволяет закодировать 65536 символов. В
результате были созданы группы символов различных
языков.
Символы стандарта Unicode
называют широкими, а
обычные 8-разрядные узкими.
36
37.
Кодирование в АSCI IСимволКод16 Символ
Пробел
20
@
!
21
А
“
22
В
Код16
40
41
42
Кодирование в в UNICODE
000016 -007F16 – код ASCII;
010016 -017F16 европейские латинские;
040016 -04FF16 кириллица.
37
38.
Кодирование графической информацииЭкран дисплейного монитора представляется как набор
отдельных точек -пикселей (pixels elements). Число пикселей
отражается парой чисел, первое из которых показывает
количество пикселей в одной строке, а второе - число строк
(например, 320 х 200).
Каждому пикселю ставится в соответствие фиксированное
количество битов (атрибутов пикселя) в некоторой области
памяти, которая называется видеопамятью.
Атрибуты пикселя определяют цвет и яркость каждой точки
изображения на экране монитора дисплея.
38
39.
Монохромное изображениеЕсли для атрибутов пикселя отводится один бит, то графика
является двухцветной, например, черно-белой (нулю соответствует
черный цвет пикселя, а единице — белый цвет пикселя).
Если каждый пиксель представляется п битами, то имеем
возможность представить на экране одновременно
2n
оттенков.
В дисплеях с монохромным монитором значение атрибута
пикселя управляет яркостью точки на экране.
39
40.
Цветное изображениеВ дисплеях с цветным монитором значение атрибута пикселя
управляет интенсивностью трех составляющих, яркостями трех
цветовых компонент изображения пикселя.
При этом используется разделение цвета на RGB - компоненты
— красную, зеленую и синюю.
Если каждая компонента имеет N градаций, то общее
количество цветовых оттенков составляет N x N x N, при этом в
число цветовых оттенков включаются белый, черный и
градации серого цвета.
40
41.
Цветное изображениеR
G
B
R
Красный
G
Зеленый
B
Синий
R+G
Желтый
G+B
Голубой
R+B
Пурпурный
R+G+B
Белый
41
42.
ВидеопамятьВ
процессе
формирования
изображения
обеспечивается периодическое считывание видеопамяти и
преобразование
значений
атрибутов
пикселей
в
последовательность сигналов, управляющих яркостью точек,
отвечающих за RGB – компоненты каждого пикселя
монитора.
В видиопамяти может размещаться несколько страниц
дисплея. Переход от воспроизведения одной страницы к
воспроизведению
другой
страницы
производится
практически мгновенно.
42
43.
Определение объема видеопамятиНеобходимый объем видеопамяти
формуле:
P можно определить по
P = m n b s / 8 (байт)
где m количество пикселей в строке экрана;
n количество строк пикселей;
b количество двоичных разрядов, используемых для
кодирования цвета одного пикселя;
s количество страниц видеопамяти.
43
44.
Представление звуковой информацииЗвуковая информация в компьютере представляется
двумя способами:
-как набор выборок звукового сигнала (оцифрованный
звук);
-как набор команд для синтеза звука с помощью
музыкальных инструментов.
44
45.
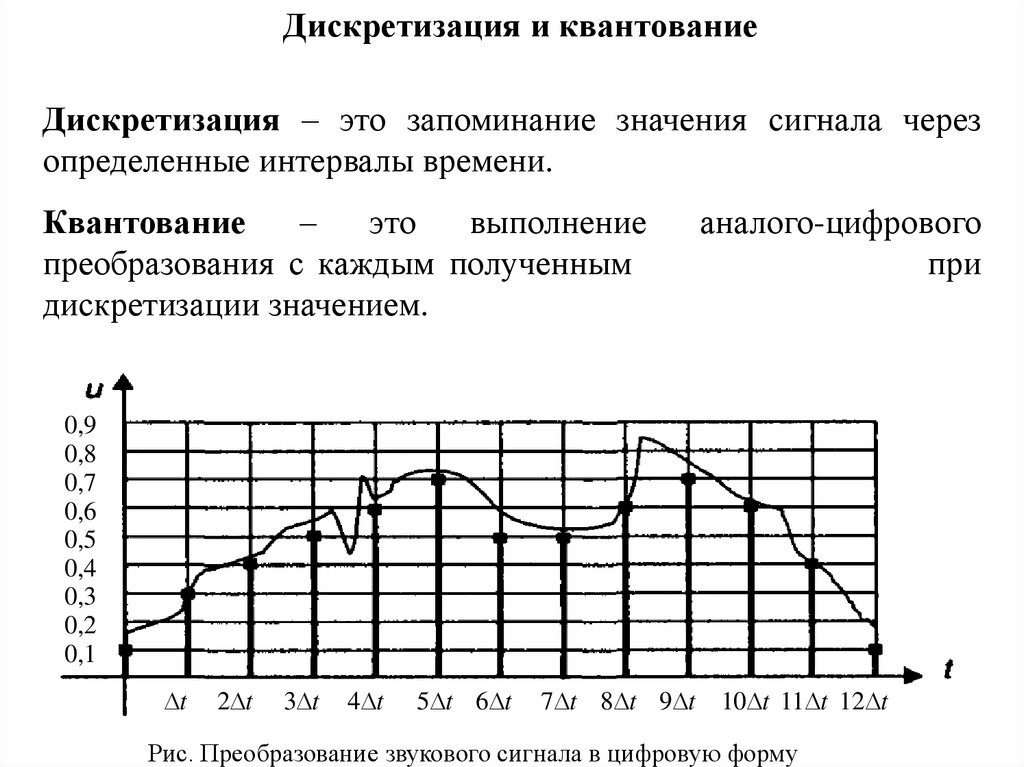
Дискретизация и квантованиеДискретизация – это запоминание значения сигнала через
определенные интервалы времени.
Квантование
–
это
выполнение
преобразования с каждым полученным
дискретизации значением.
аналого-цифрового
при
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
t
2 t
3 t
4 t
5 t 6 t
7 t 8 t 9 t 10 t 11 t 12 t
Рис. Преобразование звукового сигнала в цифровую форму
45
46.
Квантование сигналаU
N
U
где U – величина преобразуемого значения,
U – наименьшее возможное значение, отличное от нуля
(величина кванта).
При выполнении преобразования дробная часть значения N
отбрасывается.
46
47.
Пример квантованияВыполнить квантование и дискретизацию сигнала,
изображенного на рис.
Интервал дискретизации равен t, величина кванта – 0,1
В. Последовательность преобразованных значений записать в
файл в двоичной форме.
В результате квантования и дискретизации получается
следующая последовательность значений: 1, 3, 4, 5, 6, 7, 5, …
.
Если преобразовать данные значения в 8-разрядные
двоичные числа, то в память будет записано:
00000001000000110000010000000101000001100000011100000
101…
47
48.
Объем памяти при хранения звукового сигналаf n k
1
Q
t 60, f
8
t
где f – частота дискретизации (Гц, 1/с);
t – интервал дискретизации (с);
n – разрядность квантованных значений
двоичной форме (бит);
в
k – режим воспроизведения (1 – стерео, 2 – моно);
t – время воспроизведения (мин).
48
49.
Пример определения объема памятиОпределить
объем
данных
в
звуковом
файле,
воспроизводимом 10 мин с частотой 22050 выборок в
секунду и 8 битовыми значениями выборки по одному
(моно) и двум каналам (стерео).
49
50.
Определение объема памяти для монозвучания22050 8 1
Q
10 60
8
=
= 13230000 байт ≈ 12.6 Мб.
Определение объема памяти для стереозвучания
22050 8 2
Q
10 60 =
8
= 26460000 байт ≈ 25.2 Мб.
50
51.
Способ с использованием синтезаторов музыкальныхинструментов
Хранится последовательность событий (нажатие клавиш
музыкантом) вместе
с синхронизирующей информацией,
которая обеспечивают требуемое звучание инструментов при воспроизведении музыкального произведения.
51
52.
Хранение видеоинформацииВидеофайл представляет собой последовательность кадров
изображения (видеопоток) и звуковых данных (аудиопоток),
которые должны воспроизводиться через определенные
промежутки времени. Объем памяти:
Q t ( RV SV R A S A )
где t – время воспроизведения файла (с);
RV – скорость воспроизведения данных видеопотока (Гц, 1/с);
SV – размер дискретизованной величины для видеопотока (байт);
RA – скорость воспроизведения данных аудиопотока (Гц, 1/с);
SA – размер дискретизованной величины для аудиопотока (байт).
52
53.
Пример определения объема видеоинформацииОпределим объем видеофайла, содержащего информацию,
воспроизводимую 10 мин при значениях RV = 30 Гц, SV
= 20000 байт, RA = 22050 Гц, SA = 8 байт.
Q ≈ = 465840000 байтов ≈ 444.3 Мб.
53



















































 Информатика
Информатика








