Похожие презентации:
Basic Concepts of Complex Numbers
1. Basic Concepts of Complex Numbers
There are no real numbers for the solution ofthe equation
2
x 1.
To extend the real number system to include
such numbers as,
1,
the number i is defined to have the following
property;
2
i 1.
2. Basic Concepts of Complex Numbers
So… i 1The number i is called the imaginary unit.
Numbers of the form a + bi, where a and b
are real numbers are called complex
numbers.
In this complex number, a is the real part
and b is the imaginary part.
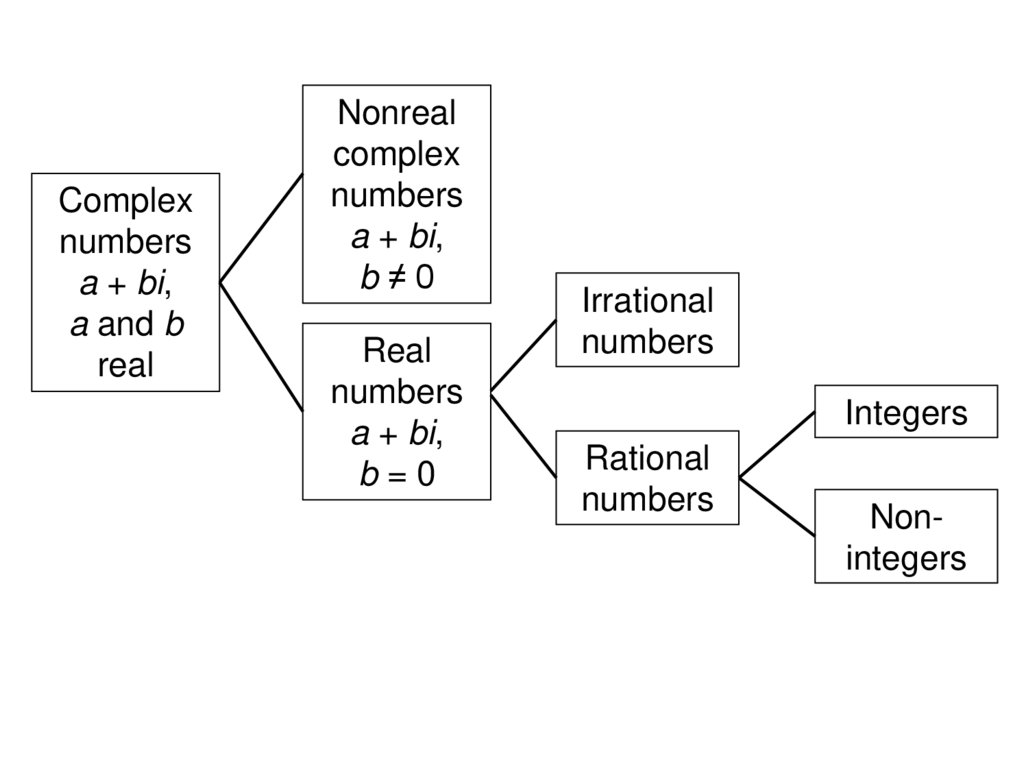
3.
Complexnumbers
a + bi,
a and b
real
Nonreal
complex
numbers
a + bi,
b≠0
Real
numbers
a + bi,
b=0
Irrational
numbers
Integers
Rational
numbers
Nonintegers
4. Basic Concepts of Complex Numbers
Two complex numbers are equal providedthat their real parts are equal and their
imaginary parts are equal;
a bi c di if and only if a c and b d
5. Basic Concepts of Complex Numbers
For complex number a + bi, if b = 0, thena + bi = a
So, the set of real numbers is a subset of
complex numbers.
6. Basic Concepts of Complex Numbers
If a = 0 and b ≠ 0, the complex number is pureimaginary.
A pure imaginary number or a number, like 7 +
2i with a ≠ 0 and b ≠ 0, is a nonreal complex
number.
The form a + bi (or a + ib) is called standard
form.
7.
THE EXPRESSIONa
If a 0, then a i a.
8. Example 1
WRITINGa AS i a
Write as the product of a real number and i,
using the definition of a.
a.
16
Solution:
16 i 16 4i
9. Example 1
WRITINGa AS i a
Write as the product of a real number and i,
using the definition of a.
b.
70
Solution:
70 i 70
10. Example 1
WRITINGa AS i a
Write as the product of a real number and i,
using the definition of a.
c.
48
Solution:
48 i 48 i 16 3 4i 3
Product rule
for radicals
11. Operations on Complex Numbers
Caution In particular, the rulec
d cd
is valid only when c and d are not both
negative.
( 4)( 9) 36 6,
while
4
9 2i (3i ) 6i 2 6
so
4
9 ( 4)( 9).
12. Example 2
FINDING PRODUCTS ANDQUOTIENTS INVOLVING
NEGATIVE RADICALS
Multiply or divide, as indicated. Simplify
each answer.
a.
7
7
Solution:
7
First write all square
roots in terms of i.
7 i 7 i 7
i
2
7
1 7
7
2
i 2 = −1
13. Example 2
FINDING PRODUCTS ANDQUOTIENTS INVOLVING
NEGATIVE RADICALS
Multiply or divide, as indicated. Simplify
each answer.
b.
6
10
Solution:
6
10 i 6 i 10
i
2
60
1 4 15
1 2 15
2 15
14. Example 2
FINDING PRODUCTS ANDQUOTIENTS INVOLVING
NEGATIVE RADICALS
Multiply or divide, as indicated. Simplify
each answer.
20
c.
2
Solution:
20 i 20
20
10
2
2
i 2
Quotient
rule for
radicals
15. Example 3
SIMPLIFYING A QUOTIENTINVOLVING A NEGATIVE
RADICAND
Write 8 128
4
Solution:
in standard form a + bi.
8 128 8 64 2
4
4
8 8i 2
4
64 8i
16. Example 3
SIMPLIFYING A QUOTIENTINVOLVING A NEGATIVE
RADICAND
Write 8 128
4
Solution:
Be sure to
factor before
simplifying
in standard form a + bi.
8 8i 2
4
4 2 2i 2
4
2 2i 2
64 8i
Factor.
Lowest terms
17.
Addition and Subtraction ofComplex Numbers
For complex numbers a + bi and c + di,
(a bi ) (c di ) (a c ) (b d )i
and (a bi ) (c di ) (a c ) (b d )i .
18. Example 4
ADDING AND SUBTRACTINGCOMPLEX NUMBERS
Find each sum or difference.
a. (3 4i ) ( 2 6i )
Solution:
Add real
parts.
Add
imaginary
parts.
(3 4i ) ( 2 6i ) 3 ( 2) 4 6 i
Commutative, associative,
distributive properties
1 2i
19. Example 4
ADDING AND SUBTRACTINGCOMPLEX NUMBERS
Find each sum or difference.
b. ( 9 7i ) (3 15i )
Solution:
( 9 7i ) (3 15i ) 6 8i
20. Example 4
ADDING AND SUBTRACTINGCOMPLEX NUMBERS
Find each sum or difference.
c. ( 4 3i ) (6 7i )
Solution:
( 4 3i ) (6 7i ) ( 4 6) 3 ( 7) i
10 10i
21. Example 4
ADDING AND SUBTRACTINGCOMPLEX NUMBERS
Find each sum or difference.
d. (12 5i ) (8 3i )
Solution:
(12 5i ) (8 3i ) 4 2i
22. Multiplication of Complex Numbers
The product of two complex numbers isfound by multiplying as if the numbers were
binomials and using the fact that i2 = –1, as
follows.
FOIL
(a bi )(c di ) ac adi bic bidi
ac adi bci bdi
2
Distributive property;
ac (ad bc )i bd ( 1)
i 2 = –1
(ac bd ) (ad bc )i
23.
Multiplication of ComplexNumbers
For complex numbers a + bi and c + di,
(a bi )(c di ) (ac bd ) (ad bc )i .
24. Example 5
MULTIPLYING COMPLEXNUMBERS
Example 5
Find each product.
a. (2 3i )(3 4i )
Solution:
(2 3i )(3 4i ) 2(3) 2(4i ) 3i (3) 3i (4i ) FOIL
6 8i 9i 12i
6 i 12( 1)
18 i
2
i2 = −1
25. Example 5
MULTIPLYING COMPLEXNUMBERS
Find each product.
2
(4
3
i
)
b.
Solution:
2
2
2
(4 3i ) 4 2(4)(3i ) (3i ) Square of a binomial
16 24i 9i
2
16 24i 9( 1)
7 24i
Remember to add twice the
product of the two terms.
i 2 = −1
26. Example 5
MULTIPLYING COMPLEXNUMBERS
Example 5
Find each product.
c. (6 5i )(6 5i )
Solution:
(6 5i )(6 5i ) 6 (5i )
2
2
36 25( 1)
Product of the sum
and difference of
two terms
i 2 = −1
36 25
61, or 61 0i
Standard form
27. Simplifying Powers of i
Powers of i can be simplified using the factsi 2 1 and i 4 ( i 2 )2 ( 1)2 1
28. Example 6
SIMPLIFYING POWERS OF iExample 6
Simplify each power of i.
a. i 15
Solution:
Since i 2 = –1 and i 4 = 1, write the given
power as a product involving i 2 or i 4. For
example, i 3 i 2 i ( 1) i i .
Alternatively, using i4 and i3 to rewrite i15 gives
i
15
i
12
i i
3
4
3
i 1 ( i ) i
3
3
29. Example 6
SIMPLIFYING POWERS OF iExample 6
Simplify each power of i.
b. i 3
Solution:
i
3
i
4
4 1
i (i )
i (1)
1
i i
30.
Powers of ii i
5
i i
i i
2
i 1
6
i 1
i
10
i i
7
i i
i i
i 1
i 1
12
1
3
4
8
9
1
11
i
1, and so on.
31.
Property of ComplexConjugates
For real numbers a and b,
(a bi )(a bi ) a 2 b 2 .
32. Example 7
DIVIDING COMPLEX NUMBERSWrite each quotient in standard form a + bi.
a. 3 2i
5 i
Solution:
3 2i (3 2i )(5 i )
5 i
(5 i )(5 i )
15 3i 10i 2i 2
2
25 i
Multiply by the
complex conjugate of
the denominator in
both the numerator
and the denominator.
Multiply.
33. Example 7
DIVIDING COMPLEX NUMBERSWrite each quotient in standard form a + bi.
a. 3 2i
5 i
Solution:
15 3i 10i 2i
2
25 i
13 13i
26
2
Multiply.
i 2 = −1
34. Example 7
DIVIDING COMPLEX NUMBERSWrite each quotient in standard form a + bi.
a. 3 2i
5 i
Solution:
13 13i
26
13 13i
26 26
i 2 = −1
a bi a bi
c
c c
35. Example 7
DIVIDING COMPLEX NUMBERSWrite each quotient in standard form a + bi.
a. 3 2i
5 i
Solution:
13 13i
26 26
1 1
i
2 2
a bi a bi
c
c c
Lowest terms;
standard form
36. Example 7
DIVIDING COMPLEX NUMBERSWrite each quotient in standard form a + bi.
3
b.
i
Solution:
3 3( i )
i i ( i )
3i
2
i
– i is the conjugate of i.
37. Example 7
DIVIDING COMPLEX NUMBERSWrite each quotient in standard form a + bi.
3
b.
i
Solution:
3i
2
i
3i
1
3i , or 0 3i
i 2 = −1(−1) = 1
Standard form




































 Математика
Математика








