Электроемкость конденсатора и энергия электрического поля. (лекция 1б)

1. Лекция 1б. Электроемкость конденсатора и энергия электрического поля

Курс физики для студентов БГТУ
Заочный факультет
для специальностей ХТОМС, ХТНМС
Кафедра физики БГТУ
доцент Крылов Андрей Борисович
Часть 3.
Электричество и
постоянный ток
Лекция 1б.
Электроемкость конденсатора и энергия
электрического поля
1. Электроемкость уединенного проводника.
2. Конденсаторы, их электроемкость и соединения.
3. Энергия заряженного конденсатора.
4. Энергия заряженного проводника, электрического поля.
Плотность энергии электрического поля.
2016
1
+4

2. 1. Емкость проводников. Электроемкость уединенного проводника.

Уединенный проводник - проводник, удаленный от других проводников, тел, заряды которых
могут вызвать перераспределение зарядов на нашем проводнике.
Тогда, если проводнику сообщается заряд q, то он распределяется единственным образом
так, чтобы поле внутри проводника было равно нулю.
Если на уединенный проводник добавим еще заряд q, то он распределится аналогичным
образом, но только вырастет напряженность Е поля вблизи поверхности и потенциал φ
проводника.
Опыт показывает, что потенциал проводника пропорционален его заряду: q ~ , а значит q =
C , где коэффициент пропорциональности есть электроемкость уединенного проводника С.
Электроемкость уединенного проводника
равна заряду q, сообщение которого проводнику
изменяет его потенциал
на 1 Вольт:
Фарад − очень большая ёмкость для уединённого проводника. Емкостью 1 Ф обладал бы
уединённый металлический шар, радиус которого равен 13 радиусам Солнца. Ёмкость же шара
размером с Землю, используемого как уединённый проводник, составляла бы около 710
микрофарад. Поэтому используют более мелкие величины: от миллифарад (1 мФ=10-3Ф)
до пикофарад (1 пФ =10-12Ф) .
Тогда
электроемкость
шара
Для примера найдем электроемкость шара в общем виде.
Рассмотрим металлический шар радиуса R.
Пусть этот шар равномерно заряжен зарядом q, тогда его
потенциал равен:
2
+10

3. Взаимная емкость двух проводников. Конденсаторы

Если двум изолированным друг от друга проводникам сообщить заряды q1 и q2, то
между ними возникает разность потенциалов Δφ, зависящая от величин зарядов и
геометрии проводников.
Разность потенциалов Δφ между двумя точками в электрическом поле часто называют
напряжением U.
Наибольший практический интерес представляет случай, когда заряды проводников
одинаковы по модулю и противоположны по знаку: q1 = – q2 = q. В этом случае можно
ввести понятие электрической емкости.
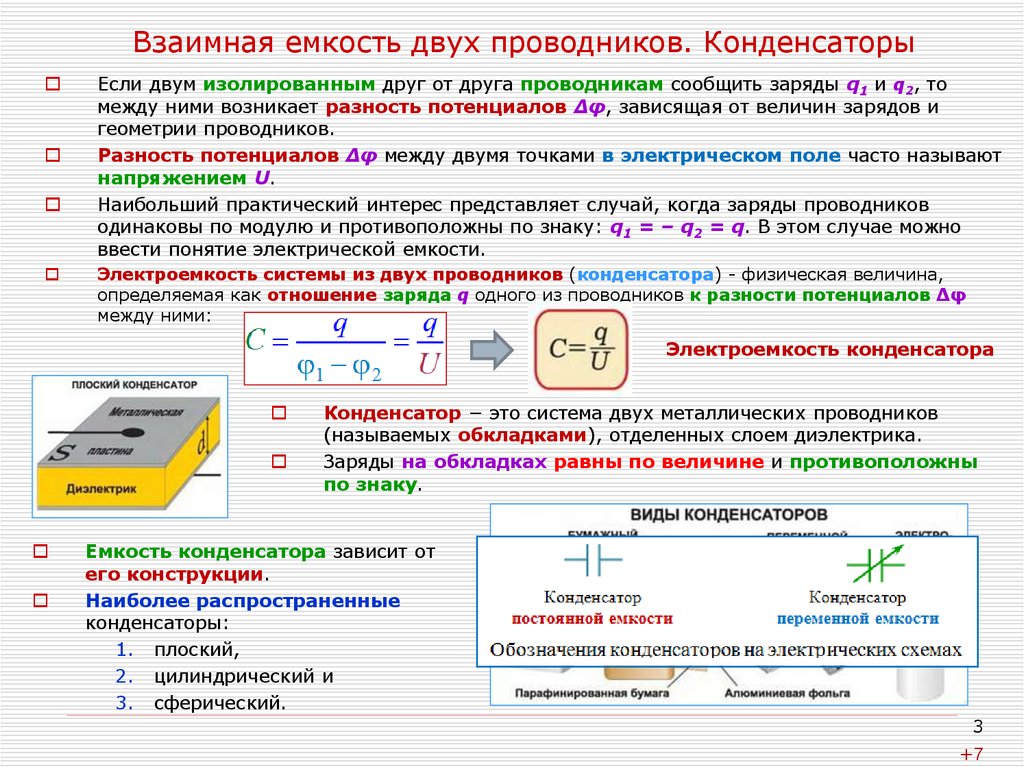
Электроемкость системы из двух проводников (конденсатора) - физическая величина,
определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ
между ними:
Электроемкость конденсатора
Конденсатор − это система двух металлических проводников
(называемых обкладками), отделенных слоем диэлектрика.
Заряды на обкладках равны по величине и противоположны
по знаку.
Емкость конденсатора зависит от
его конструкции.
Наиболее распространенные
конденсаторы:
1. плоский,
2. цилиндрический и
3. сферический.
3
+7

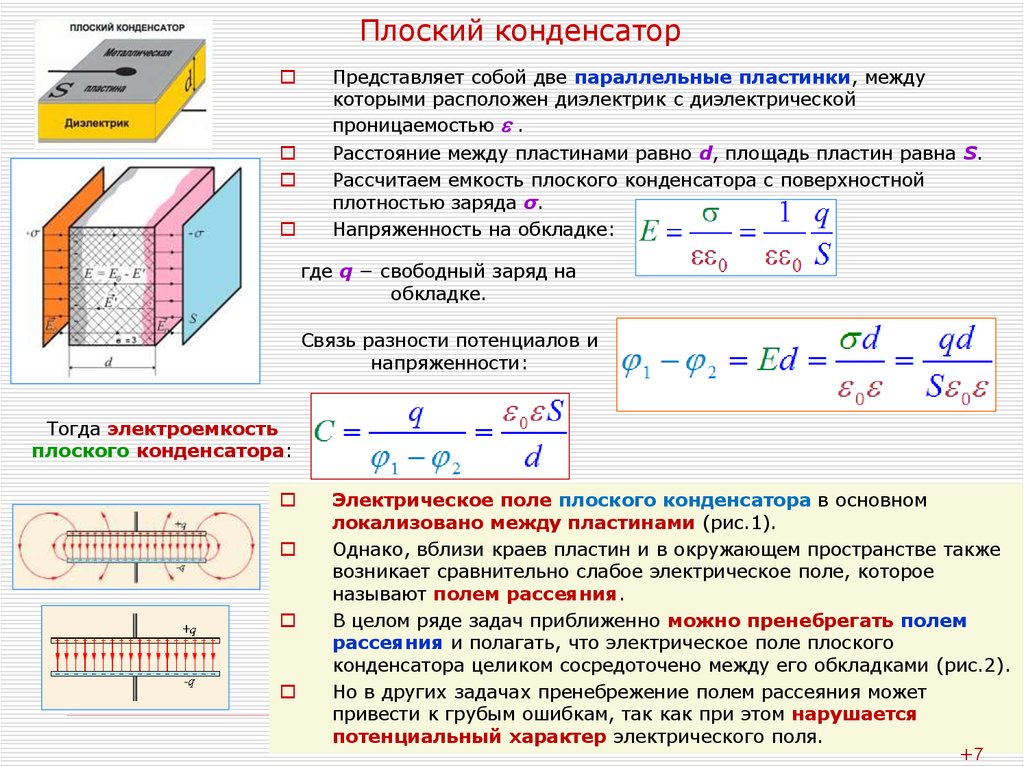
4. Плоский конденсатор

Представляет собой две параллельные пластинки, между
которыми расположен диэлектрик с диэлектрической
проницаемостью .
Расстояние между пластинами равно d, площадь пластин равна S.
Рассчитаем емкость плоского конденсатора с поверхностной
плотностью заряда σ.
Напряженность на обкладке:
где q − свободный заряд на
обкладке.
Связь разности потенциалов и
напряженности:
Тогда электроемкость
плоского конденсатора:
Электрическое поле плоского конденсатора в основном
локализовано между пластинами (рис.1).
Однако, вблизи краев пластин и в окружающем пространстве также
возникает сравнительно слабое электрическое поле, которое
называют полем рассеяния.
В целом ряде задач приближенно можно пренебрегать полем
рассеяния и полагать, что электрическое поле плоского
конденсатора целиком сосредоточено между его обкладками (рис.2).
Но в других задачах пренебрежение полем рассеяния может
привести к грубым ошибкам, так как при этом нарушается
4
потенциальный характер электрического поля.
+7

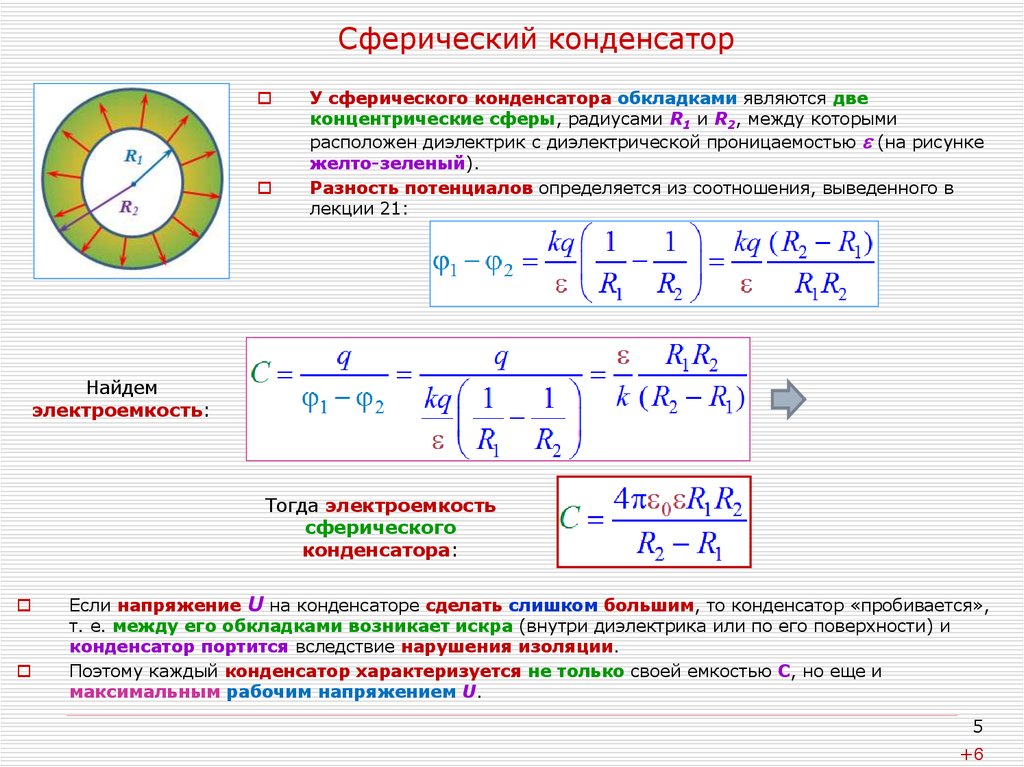
5. Сферический конденсатор

У сферического конденсатора обкладками являются две
концентрические сферы, радиусами R1 и R2, между которыми
расположен диэлектрик с диэлектрической проницаемостью (на рисунке
желто-зеленый).
Разность потенциалов определяется из соотношения, выведенного в
лекции 21:
Найдем
электроемкость:
Тогда электроемкость
сферического
конденсатора:
Если напряжение U на конденсаторе сделать слишком большим, то конденсатор «пробивается»,
т. е. между его обкладками возникает искра (внутри диэлектрика или по его поверхности) и
конденсатор портится вследствие нарушения изоляции.
Поэтому каждый конденсатор характеризуется не только своей емкостью С, но еще и
максимальным рабочим напряжением U.
5
+6

6. Цилиндрический конденсатор

У цилиндрического конденсатора обкладками являются два
коаксиальных цилиндра радиусами R1 и R2, а длина цилиндров равна l
(причем l много больше расстояния между обкладками). Между ними
расположен диэлектрик с диэлектрической проницаемостью .
Напряженность поля Е внутри цилиндрического конденсатора (между
цилиндрами):
где r − расстояние от оси симметрии цилиндров;
− заряд, приходящийся на единицу длины
одного из цилиндров.
Тогда разность потенциалов равна:
Тогда по определению электроемкость
конденсатора:
Электроемкость
цилиндрического
конденсатора
Электроемкость
цилиндрического
конденсатора
на единицу его длины
6
+6

7. 2. Конденсаторы и их соединения

Чтобы получить желаемую емкость при нужном рабочем напряжении, располагая
определенными конденсаторами, конденсаторы соединяют в батареи.
Соединения конденсаторов
Параллельное соединение
Для всех конденсаторов
напряжение U одинаковое
Суммарный заряд, находящийся
на батарее:
Емкость батареи
Смешанное соединение
Емкость такой батареи
легко определить,
шаг за шагом
обсчитывая
параллельные и
последовательные
части электрической
схемы.
Вывод: так как напряжение на каждом
конденсаторе равно напряжению на
батарее, то и допустимое рабочее
напряжение батареи такое же, как и у
одного конденсатора.
Последовательное соединение
Для всех конденсаторов заряд q
одинаковый
Напряжение же батареи будет равно
сумме напряжений на отдельных
конденсаторах:
Емкость батареи
Вывод: так как напряжение на каждом
конденсаторе будет меньше напряжения на
батарее, то допустимое рабочее
напряжение будет больше, чем у одного
7
конденсатора. Возможен пробой!!!
+11

8. Энергия конденсатора

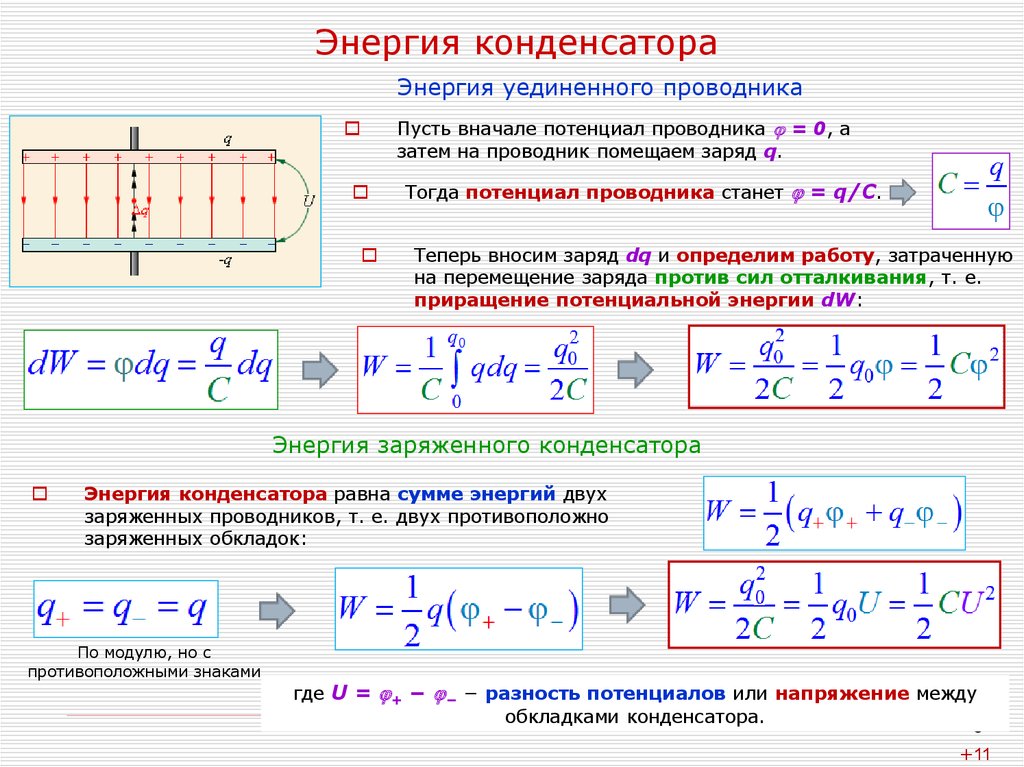
Энергия уединенного проводника
Пусть вначале потенциал проводника = 0, а
затем на проводник помещаем заряд q.
Тогда потенциал проводника станет = q/C.
Теперь вносим заряд dq и определим работу, затраченную
на перемещение заряда против сил отталкивания, т. е.
приращение потенциальной энергии dW:
Энергия заряженного конденсатора
Энергия конденсатора равна сумме энергий двух
заряженных проводников, т. е. двух противоположно
заряженных обкладок:
По модулю, но с
противоположными знаками
где U = + − − − разность потенциалов или напряжение между
обкладками конденсатора.
8
+11

9. 4. Энергия и плотность энергии электрического поля

Энергия электрического поля W в плоском конденсаторе
Емкость плоского конденсатора:
Энергия, запасаемая в плоском конденсаторе:
Выразим энергию
где
W через напряженность электрического поля Е внутри конденсатора:
Плотность энергии w электрического поля
Плотность энергии w
электрического поля - это энергия,
приходящаяся на единицу объема:
Объем V можно сделать сколь угодно малым, настолько, что поле внутри этого объема можно
считать однородным, т. е. E − постоянным.
Тогда:
где - объемная плотность,
- поверхностная плотность зарядов
где интегрирование в правой части ведется по объему,9в
котором напряженность поля Е отлично от нуля.
+13

10. Спасибо за внимание!

Курс физики для студентов БГТУ
Заочный факультет
Кафедра физики БГТУ
доцент Крылов Андрей Борисович
Часть 3.
Электричество и
постоянный ток
Спасибо за внимание!
10
+2