Изучение показатели изменчивости

1.

Дисциплина: «Бизнес-статистика»
5.
Тема 5. Изучение
показатели изменчивости
Лекция
разнообразия,
Шпилькина Татьяна Анатольевна
кандидат экономических наук,
доцент, преподаватель ИМЭС

2.

Бизнес – статистика подразумевает применение статистических методов учета и анализа на уровне отдельной фирмы
(предприятия) в целях оценки и анализа состояния и развития локального рынка, характеристики собственного рыночного
потенциала и коммерческих возможностей, информационно-аналитического обеспечения разработки инвестиционной,
производственной и торговой программ.
План изучения Темы 4
Тема 5. Изучение
разнообразия, показатели
изменчивости.
1. Определение для стандартного
отклонения и дисперсии,
интерпретация стандартного
отклонения для нормального
распределения.
2. Определение основных
показателей вариации,
перцентили.
3. Коэффициент вариации.

3.

Список основной
литературы
Ознакомиться с литературой можно
через электронную среду
1. Бизнес-статистика: учебник и практикум для вузов / И.И. Елисеева [и др.] ;
под редакцией И.И. Елисеевой. — 2-е изд., перераб. и доп. — Москва :
Издательство Юрайт, 2022. — 444 с. — (Высшее образование). — ISBN 978-5534-14822-0. — Текст : электронный // Образовательная платформа Юрайт
[сайт]. — URL: https://urait.ru/bcode/490172
2. Статистика: учебник для вузов / под редакцией И. И. Елисеевой. — 3-е изд.,
перераб. и доп. — Москва : Издательство Юрайт, 2022. — 361 с. — (Высшее
образование). — ISBN 978-5-534-04082-1. — Текст: электронный //
Образовательная платформа Юрайт [сайт]. — URL: https://urait.ru/bcode/488653
3. Статистика. Практикум: учебное пособие для академического бакалавриата /
И. И. Елисеева [и др.] ; под редакцией И. И. Елисеевой. — Москва :
Издательство Юрайт, 2019. — 514 с. — (Бакалавр. Академический курс). —
ISBN 978-5-9916-3688-9. — URL : https://urait.ru/bcode/425262
4. Шимко, П.Д. Теория статистики : учебник и практикум для вузов /
П.Д. Шимко. — Москва : Издательство Юрайт, 2021. — 254 с. — (Высшее
образование). — ISBN 978-5-9916-9066-9. — URL : https://urait.ru/bcode/469760

4.

1. Определение для стандартного отклонения и дисперсии, интерпретация
стандартного отклонения для нормального распределения
Перцентили играют важную роль в получении обобщающих характеристик
распределения. Их можно рассматривать как показатели, разбивающие данные на
определенные части. Чаще всего в исследованиях разбивают совокупность на 4, 10 и
100 равных частей.
Так, разбиение совокупности на четыре группы означает, что в каждой группе будет
по 25% наблюдений. Границы, отмеряющие 25, 50, 75% наблюдений,
называются квартилями.
Разбиение совокупности на 10 равных групп называется децильным разбиением. В
этом случае в каждой группе содержится по 10% наблюдений, а границы, отмеряющие
каждые 10%, называются децилями распределения. Значения признака, делящие
совокупность на 100 равных частей, называются перцентилями распределения.
Перцентиль показывает точку, ниже которой находится определенный процент
наблюдений.
25-й перцентиль представляет собой первый квартиль, 50-й перцентиль — это
второй квартиль, или медиана, 90-й перцентиль — это 9-й дециль и т.д.

5.

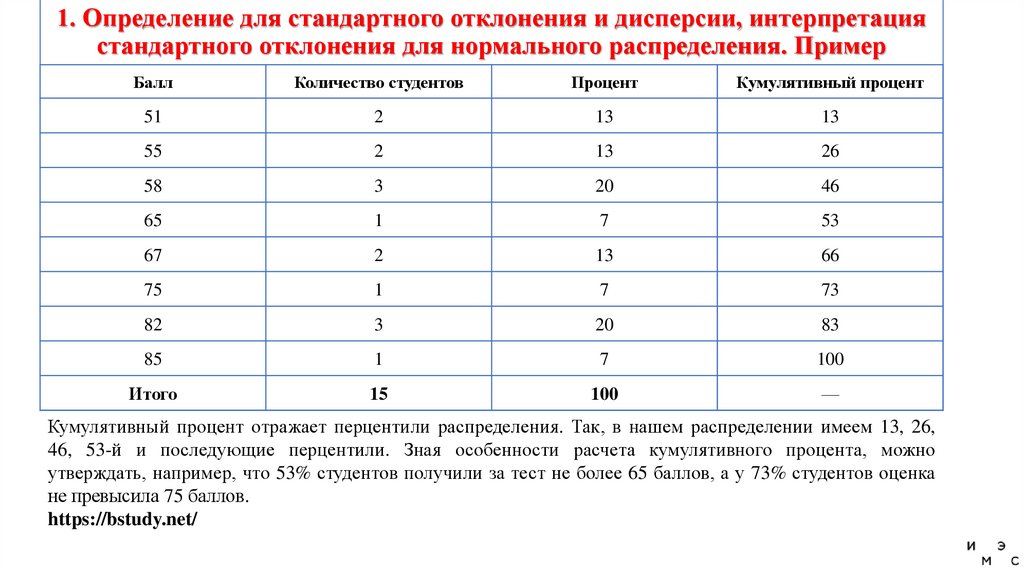
1. Определение для стандартного отклонения и дисперсии, интерпретация
стандартного отклонения для нормального распределения. Пример
Балл
Количество студентов
Процент
Кумулятивный процент
51
2
13
13
55
2
13
26
58
3
20
46
65
1
7
53
67
2
13
66
75
1
7
73
82
3
20
83
85
1
7
100
Итого
15
100
—
Кумулятивный процент отражает перцентили распределения. Так, в нашем распределении имеем 13, 26,
46, 53-й и последующие перцентили. Зная особенности расчета кумулятивного процента, можно
утверждать, например, что 53% студентов получили за тест не более 65 баллов, а у 73% студентов оценка
не превысила 75 баллов.
https://bstudy.net/

6.

1. Определение для стандартного отклонения и дисперсии, интерпретация
стандартного отклонения для нормального распределения
Для измерения вариации признака используются абсолютные и относительные показатели. К
числу абсолютных показателей относится:
1. Размах вариации, который можно определить по формуле:
R = Хмах – Хмин
где Хмах - максимальное значение признака в совокупности,
Хмин - минимальное значение.
Размах вариации является важным показателем колеблемости признака, при этом, он дает
возможность увидеть только крайние отклонения без учета всех изменений варьирующего
признака в пределах совокупности, что ограничивает область применения.
Недостатком показателя является то, что очень высокие и низкие значения признака по
сравнению с основной массой значений в совокупности могут быть обусловлены случайными
причинами. В этом случае размах вариации дает искаженную амплитуду колебаний.
2. Среднее линейное отклонение. Это средняя арифметическая из абсолютных значений
отклонений варьирующего признака от средней величины. Так как сумма отклонений значений
признака от средней величины равна 0, то все отклонения берутся в их модульном значении.
α=
σ |х