Похожие презентации:
Биометрия. Лекция 1. Значение статистических методов в научных исследованиях. Типы данных
1. Биометрия (Биологическая статистика)
Жукова Анна Анатольевна,к.б.н.,
доцент кафедры общей экологии и
методики преподавания биологии
Лекции - 24 ч;
Лаб. занятия - 28 ч
По окончании – зачет в виде теста (eUniversity).
2. Источники, рекомендуемые для подготовки к зачету:
Конспект лекций и лабораторных занятийГланц С. Медико-биологическая статистика. –
М., 1999.
Лакин Г. Ф. Биометрия, 4-е изд. – М., 1990.
В. П. Боровиков «STATISTICA для студентов и
инженеров». – М., 2001.
http://www.statsoft.ru/home/textbook/default.htm
www.biometrica.tomsk.ru
www.exponenta.ru
3. ЛЕКЦИЯ 1
ЗНАЧЕНИЕ СТАТИСТИЧЕСКИХМЕТОДОВ В НАУЧНЫХ
ИССЛЕДОВАНИЯХ.
ТИПЫ ДАННЫХ
4.
1.1. Что такое«статистика»?
5. Как была сделана эта фотография?
6. Как сделать красивую фотографию?
7. Стадии получения и обработки данных
Сбор данных;Обработка (анализ);
Представление результатов
заинтересованным людям.
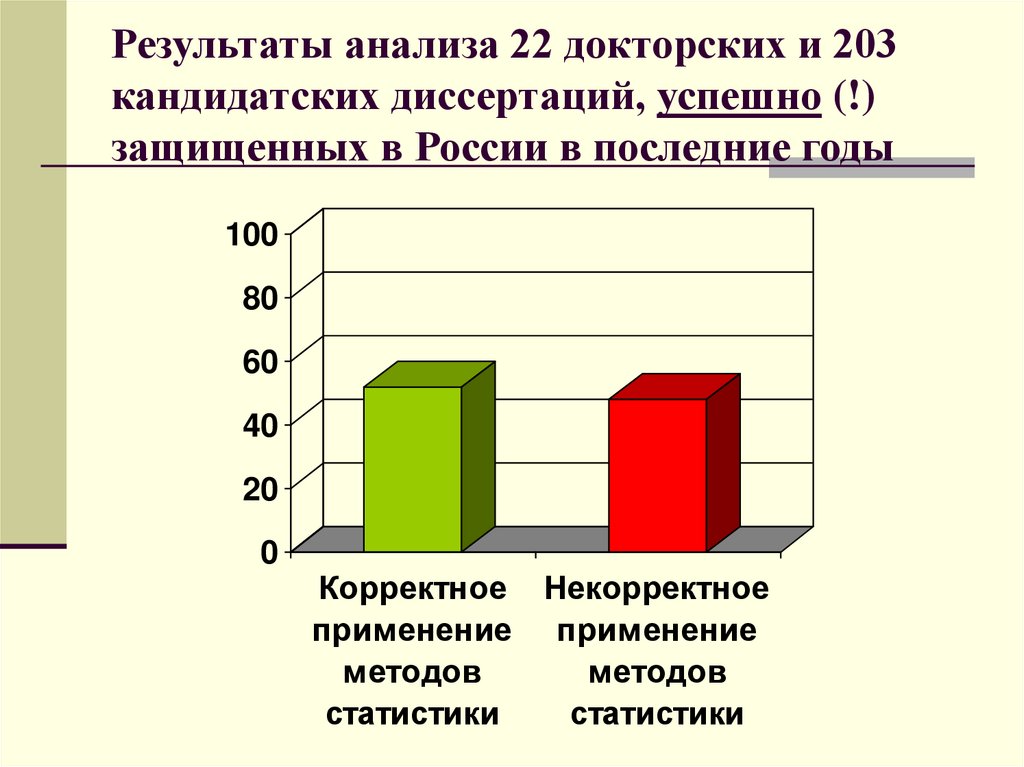
8. Результаты анализа 22 докторских и 203 кандидатских диссертаций, успешно (!) защищенных в России в последние годы
10080
60
40
20
0
Корректное Некорректное
применение применение
методов
методов
статистики
статистики
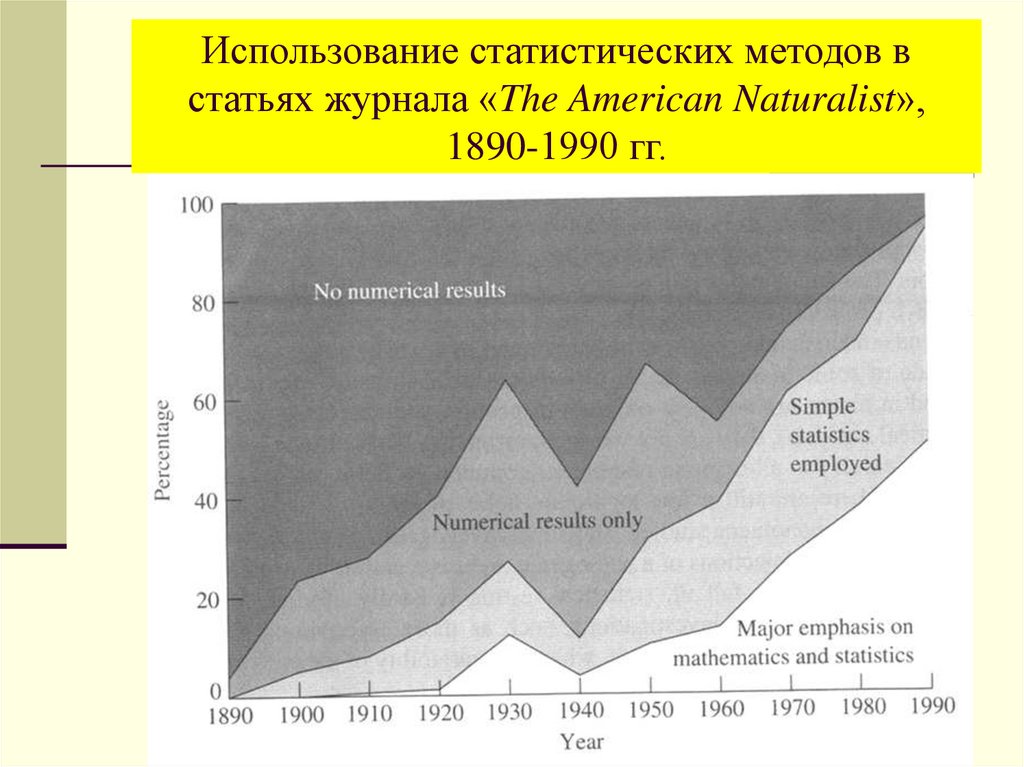
9. Использование статистических методов в статьях журнала «The American Naturalist», 1890-1990 гг.
10. Цель данного курса
Ознакомить с основнымисовременными методами статистики,
которые могут использоваться в
биологических измерениях
11. Что дает элементарная статистическая грамотность?
Возможность познания количественныхзакономерностей в биологических явлениях и
процессах;
Основы обработки экспериментальных
данных и правила корректного
представления их коллегам;
Избавление от боязни математически
оформленных статей и критический анализ
представленных в них данных;
Принципы построения математических
моделей биологических явлений и процессов.
12. «Статистика»?
Статистика занимаетсяизучением данных,
описывающих естественную
изменчивость.
13. 1.2. Краткая история развития статистики
14. Какие данные нужны были государствам в древности?
Сведения о площадяхземельных угодий, величине
налогов, численности скота и
т.п.
15. Современная статистика зародилась в XVII веке по следующим причинам:
Государствам по-прежнемунеобходимо было знать,
сколько жителей проживает в
стране, сколько из них женщин и
мужчин, сколько они платят
налогов и т.д.
16. Английские ученые, сделавшие вклад в развитие математической статистики:
Уильям Петти (William Petty)Джон Грант (John Graunt).
17. Современная статистика зародилась в XVII веке:
В связи с необходимостьюпредсказания исходов азартных
игр стала интенсивно
развиваться теория
вероятностей.
18. Ученые, внесшие большой вклад в развитие теории вероятностей:
Пьер-Симон де ЛапласКарл Фридрих Гаусс
19. XIX век:
Френсис Гальтон –«отец» биометрии.
Впервые попытался
применить методы
математической
статистики для
объяснения
биологических
явлений.
20. XIX-й век:
Карл Пирсон –продолжатель
идей Гальтона.
Внес большой
вклад в развитие
методов
описательной
статистики и
корреляционного
анализа.
21. XX век:
Рональд Фишер –выдающийся
статистик 20-го
века.
Основатель
такой важнейшей
области, как
дисперсионный
анализ.
22. 1.3. Типы данных
23. Что такое данные?
Данные – это совокупностьизмерений (наблюдений),
выполненных на объектах
одной категории по
одинаковой схеме.
24. Элементы в совокупности данных называются:
«единичное наблюдение», или«отдельное наблюдение», или
«варианта» (≠ «вариант»!)
25. Единичные наблюдения
Обозначаются хi, где i –порядковый номер в
совокупности;
«Объем» - количество
наблюдений, составляющих
совокупность. Обозначается «n»
26. Важные понятия:
Переменная (=признак) – тофактическое свойство,
которое измеряется в ходе
отдельных наблюдений.
27. Важные понятия:
«Вариация» – различие междуотдельными наблюдениями (от лат.
variatio – изменение, колебание);
«Вариабельность» - степень
различий между наблюдениями.
28. Виды ошибок
СИСТЕМАТИЧЕСКИЕСЛУЧАЙНЫЕ
Не поддаются
влиянию человека
Поддаются коррекции
29. Типы переменных:
Количественные (дискретные инепрерывные);
Порядковые (=ранговые);
Качественные;
Производные переменные
(индексы, пропорции, проценты,
удельные скорости)
30. Примеры производных переменных:
Относительные скорости(интенсивности) – отражают
динамику того или иного
процесса в отношении к единице
времени (скорость роста
популяции, смертность,
продукция фермента и т.п.).
31. 1.4. Генеральная совокупность и выборка
32. Выборка
Выборка (sample) совокупность из несколькихзначений определенного
признака.
33. Генеральная совокупность
Генеральная совокупность(population) - все множество
объектов определенной
категории, существующих в
мире.
Объем генеральной совокупности
обозначается «N»
34. Параметры
Параметры – это числовыепоказатели, характеризующие
свойства генеральной
совокупности.
35. Наиболее важные параметры:
Показатели, описывающие наиболее«характерное» в генеральной
совокупности, ее «центральную
тенденцию» (средние величины);
Показатели, отражающие степень
неоднородности членов
совокупности (дисперсия,
стандартное отклонение и др.).
36. «Тонкости обозначений»
Генеральнаясовокупность
Выборка
x
2
2
s
β
b
37. Выборочные показатели должны быть:
Несмещенными;Эффективными;
Состоятельными
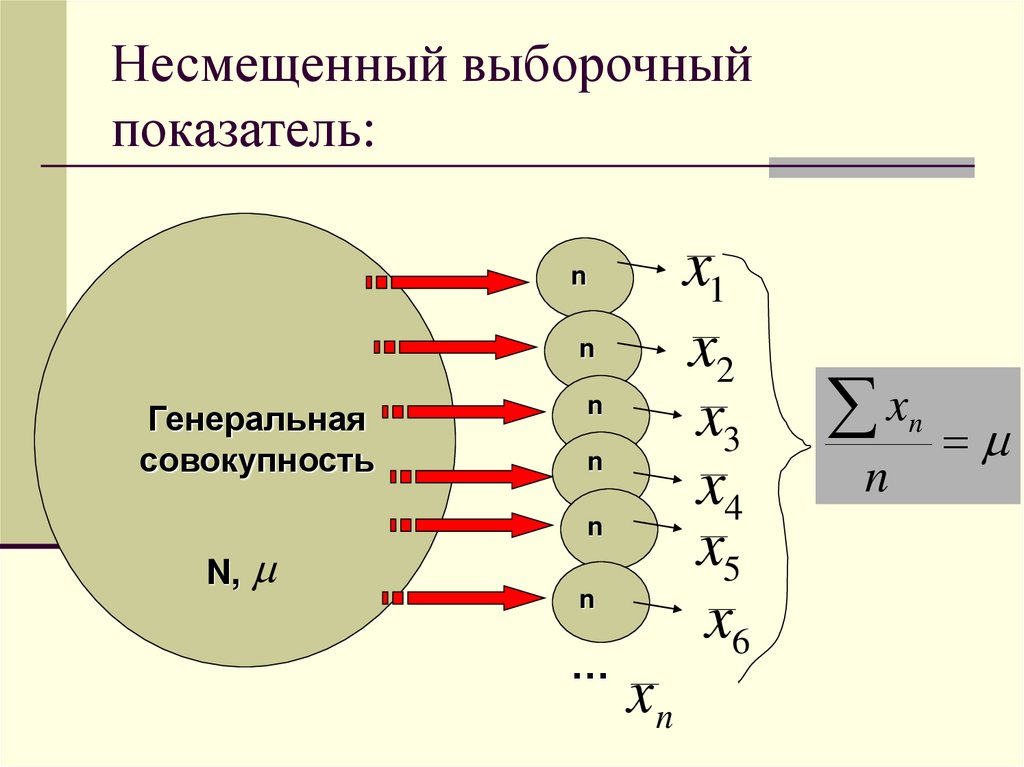
38. Несмещенный выборочный показатель:
x1x2
x3
x4
x5
x6
n
n
Генеральная
совокупность
N,
n
n
n
n
…
xn
x
n
n
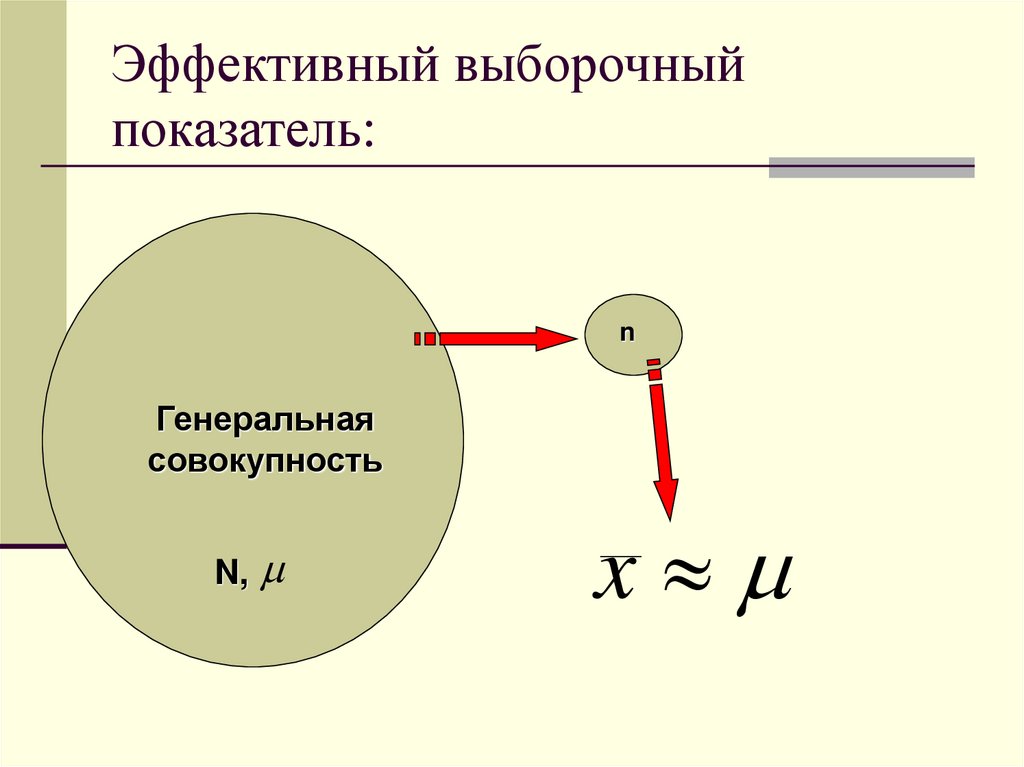
39. Эффективный выборочный показатель:
nГенеральная
совокупность
N,
x
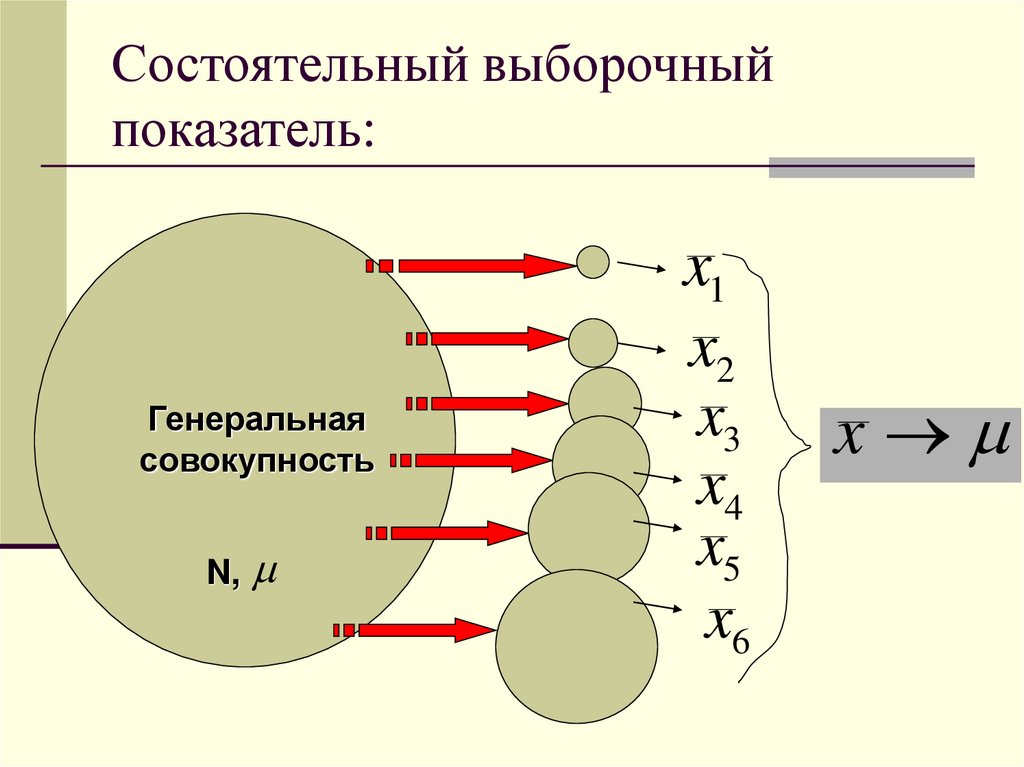
40. Состоятельный выборочный показатель:
Генеральнаясовокупность
N,
x1
x2
x3
x4
x5
x6
x
41. 1.5. Правила получения данных
42. Подходы к получению данных:
Сплошное обследование всейгенеральной совокупности;
Выборочное обследование.
43. Правила получения данных:
Для того, чтобы по выборкеможно было судить о свойствах
генеральной совокупности
необходимо организовать
случайный отбор, или
рандомизацию («random» –
случайный) объектов из
генеральной совокупности.
44. Способы рандомизации:
Простой случайный, илиполностью рандомизированный
отбор (randomized sampling).
Можно выполнить при помощи
таблиц случайных чисел.
45. Простой случайный отбор
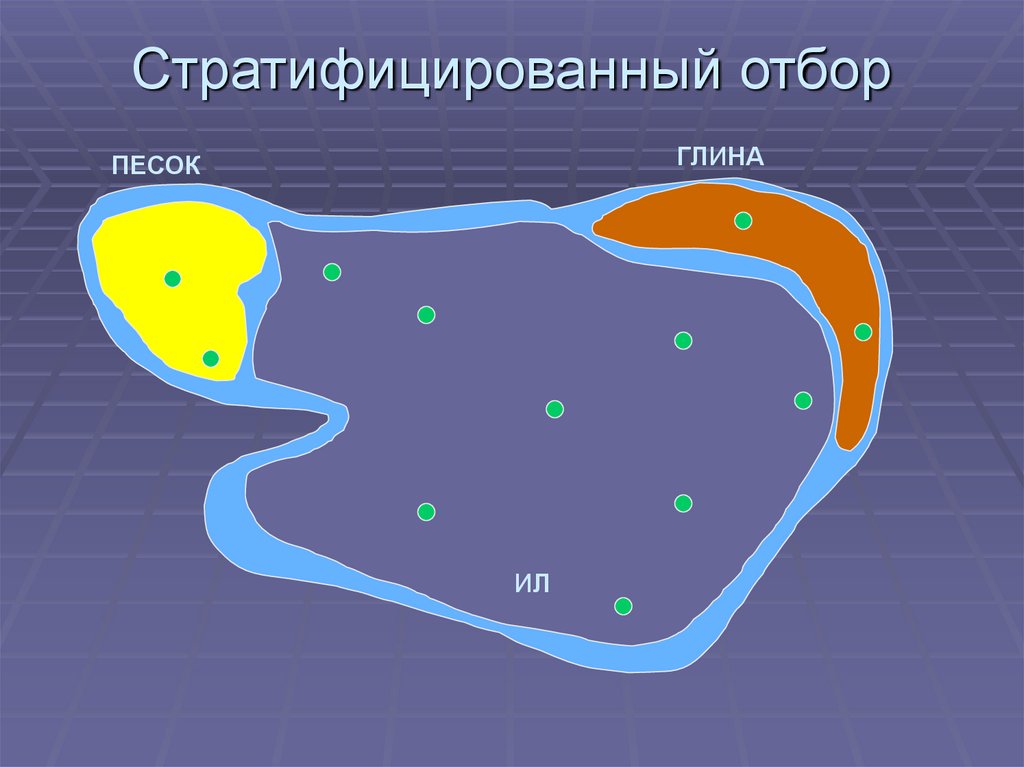
46. Способы рандомизации:
Стратифицированный отбор(stratified sampling).
Предполагает разбиение
исследуемой совокупности объектов
или пространства на схожие
подгруппы или участки (страты).
47. Стратифицированный отбор
ГЛИНАПЕСОК
ИЛ
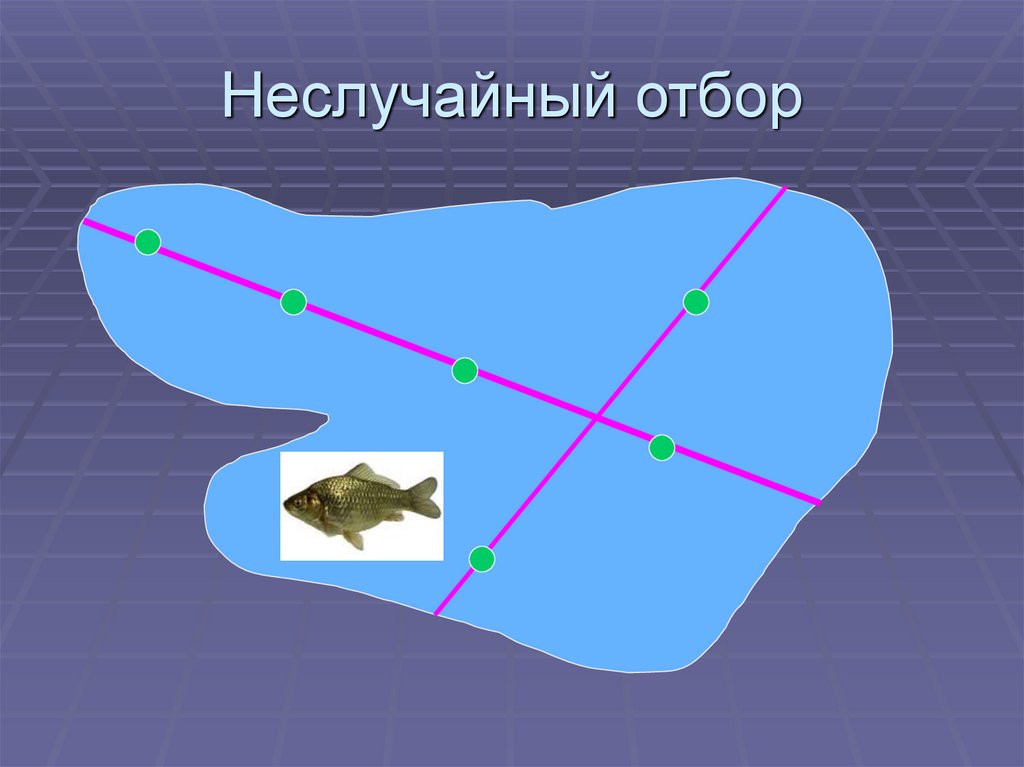
48. Способы рандомизации:
Неслучайный (=систематический,плановый) отбор (nonrandom
sampling).
Объекты для исследований выбираются
по определенной, заранее оговоренной
схеме.
49. Неслучайный отбор
50. «Репрезентативность»?
Репрезентативность – свойствовыборки правильно отражать
свойства генеральной
совокупности.
51. Смещенные выборки???
Смещенные выборки (biasedsamples)
формируются при нарушении
случайного отбора вариант из
генеральной совокупности.
52. Эксперимент Рональда Фишера:
На стол выложили 1200 камней;12 человек каждый по 3 раза
отбирали по 20 «типичных»
камней
53. Результат эксперимента Рональда Фишера:
Средний вес отобранных камнейоказался на 25% выше
истинного (66 г против 54 г);
ВЫВОД: Человек - очень плохой
инструмент для формирования
случайных выборок











































 Биология
Биология








