Похожие презентации:
Элементы математической логики. Решение логических задач. Лекция 3
1.
Основы системного анализа иматематической обработки информации
Представление информации средствами теории множеств и
математической логики
Лекция 3.
Элементы математической логики. Решение логических задач
2.
Основные понятияСлово логика означает совокупность правил,
которым подчиняется процесс мышления. Сам
термин "логика" происходит от древнегреческого
logos, означающего "слово, мысль, понятие,
рассуждение, закон".
Формальная логика - наука о формах и законах
мышления. Законы логики отражают в сознании
человека свойства, связи и отношения объектов
окружающего мира. Логика как наука позволяет
строить формальные модели окружающего мира,
отвлекаясь
от
содержательной
стороны.
Основными формами мышления являются
понятия, суждения и умозаключения
3.
К королю некоего малоизвестного королевства, очень частоприезжали различные принцы свататься к принцессам, которых
у того короля было довольно много. Каждого из них надо было
как то проверять, а так как принцев было много, то король
решил поставить процесс на поток. Он подводил принца к
дверям в комнаты и предлагал открыть одну из них. Причем в
комнатах он помещал тигров и принцесс. Принц должен был
угадать в какой комнате принцесса. Что бы это не было простое
гадание, ему выдавалась дополнительная информация,
анализируя которую он мог точно узнать где принцесса, а где
тигр. Приведем одну задачу с решением в качестве примера. В
этом испытании на дверях комнат были две таблички. Кроме
того, принцу было сказано, что на одной табличке написана
правда, а на другой нет.
1 Комната
2 Комната
В одной из этих комнат находится
В этой комнате находится принцесса, а
принцесса; кроме того, в одной из этих
в другой комнате сидит тигр.
комнат сидит тигр.
4.
Основные понятияМатематическая логика – это раздел математики,
посвященный анализу методов рассуждений, при этом
в первую очередь исследуются формы рассуждений, а
не их содержание, т.е. исследуется формализация
рассуждений. Это разновидность формальной логики,
т.е. науки, которая изучает умозаключения с точки
зрения их формального строения.
Основное неопределяемое понятие математической
логики это высказывание.
Подобно тому, как для описания действий над
переменными был разработан раздел математики
алгебра, так и для обработки логических выражений в
математической логике была создана алгебра
высказываний, или алгебра логики.
5.
Основные понятияПод
высказыванием
обычно
понимают
всякое
повествовательное предложение, утверждающее что-либо о
чем-либо, и при этом мы можем сказать, истинно оно или
ложно в данных условиях места и времени.
В математической логике не рассматривается смысл
высказываний, определяется только их логическое значение –
«истина» или «ложь». Известному немецкому математику и
логику Эрнесту Шредеру пришло в голову предложить в
качестве знака для обозначения ложного суждения цифру 0,
что, конечно, привело к обозначению истины цифрой 1.
Обозначения: A, B, C… .
Новокузнецк стоит на Томи.
Париж – столица Англии.
Карась не рыба.
Число 6 делится на 2 и на 3.
Если юноша окончил среднюю школу, то он получает
аттестат зрелости.
6.
Основные понятияМатематическая логика не интересуется содержательным
смыслом высказываний, а только лишь правилами
обращения с ними.
Поэтому отдельные высказывания, обозначенные буквами
латинского алфавита А,В,С,… называют пропозиционными
буквами
(высказывательными
переменными,
элементарными формулами, атомами и т.д. в разных
источниках).
Из таких пропозиционных букв или формул можно строить
новые, более сложные высказывания. Истинность или
ложность таких новых высказываний полностью
определяется значениями истинности (т.е. 1 или 0)
составляющих их высказываний.
Для
образования
таких
сложных
высказываний
используются пропозиционные связки (логические
операции).
7.
Основные понятияБудем называть высказывание простым
(элементарным,
атомарным),
если
оно
рассматривается нами как некое неделимое
целое. Обычно к ним относят высказывания, не
содержащие логических связок.
Сложным
(составным)
называется
высказывание, составленное из простых с
помощью логических связок.
В логике над высказываниями производятся
следующие основные операции (логические
связки): отрицание, конъюнкция, дизъюнкция,
импликация, эквиваленция.
8.
Логические операцииОтрицание (логическая связка «не»)
Отрицанием (инверсией) высказывания A
называется
высказывание,
которое
истинно, если высказывание A ложно, и
ложно, когда A истинно.
Записывается: A или ¬ A. Читается: «не A»
(«не верно, что A»).
9.
Отрицаниеявляется
логической
операцией, выполняемой над одним
аргументом. Эта логическая связка может
быть проиллюстрирована следующей
таблицей (таблицей истинности):
10.
Логические операцииСоединение двух простых высказываний A и B в
одно составное с помощью союза «и» называют
логическим умножением или конъюнкцией, а
результат операции — логическим произведением.
В русском языке в качестве операции «логическое
умножение» помимо союза «и» используются
союзы «но» и «а».
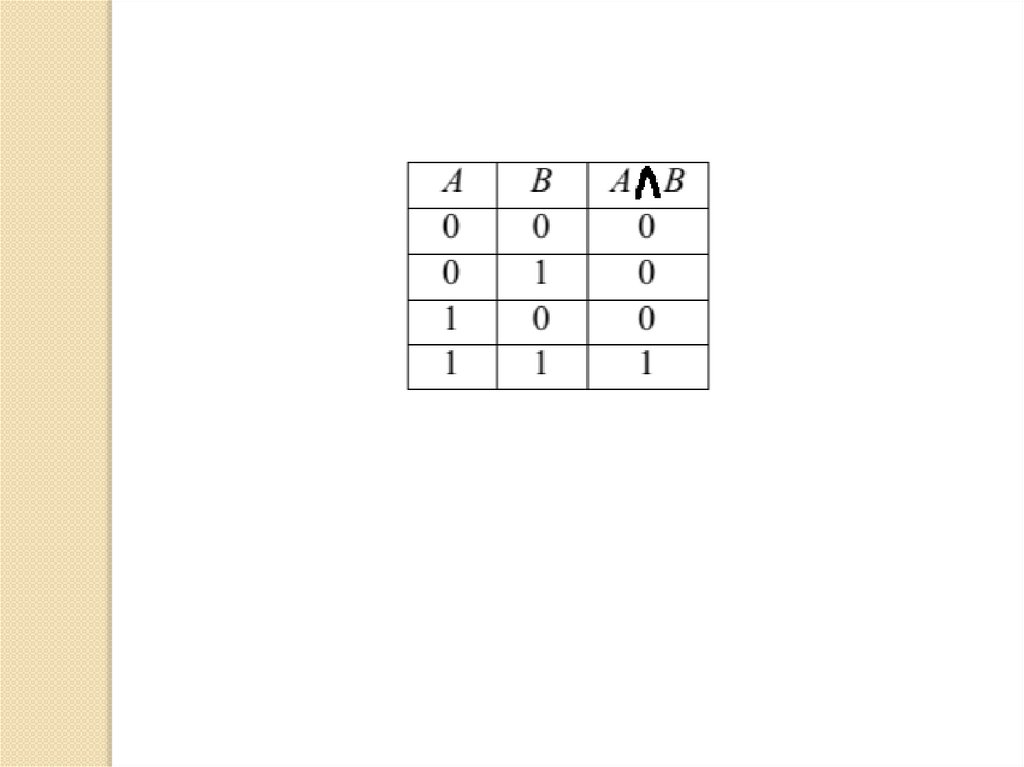
Конъюнкция двух высказываний A и B — это
сложное логическое высказывание, которое
истинно только в случае истинности всех
составляющих высказываний, в противном случае
оно ложно.
Обозначения: A&B, . A∧В
Читается: «A и B»
11.
12.
Логические операцииСоединение двух простых высказываний A и B в
одно составное с помощью союза «или»,
употребляемого в неисключающем смысле,
называется логическим
сложением или
дизъюнкцией,
а
полученное
составное
высказывание — логической суммой.
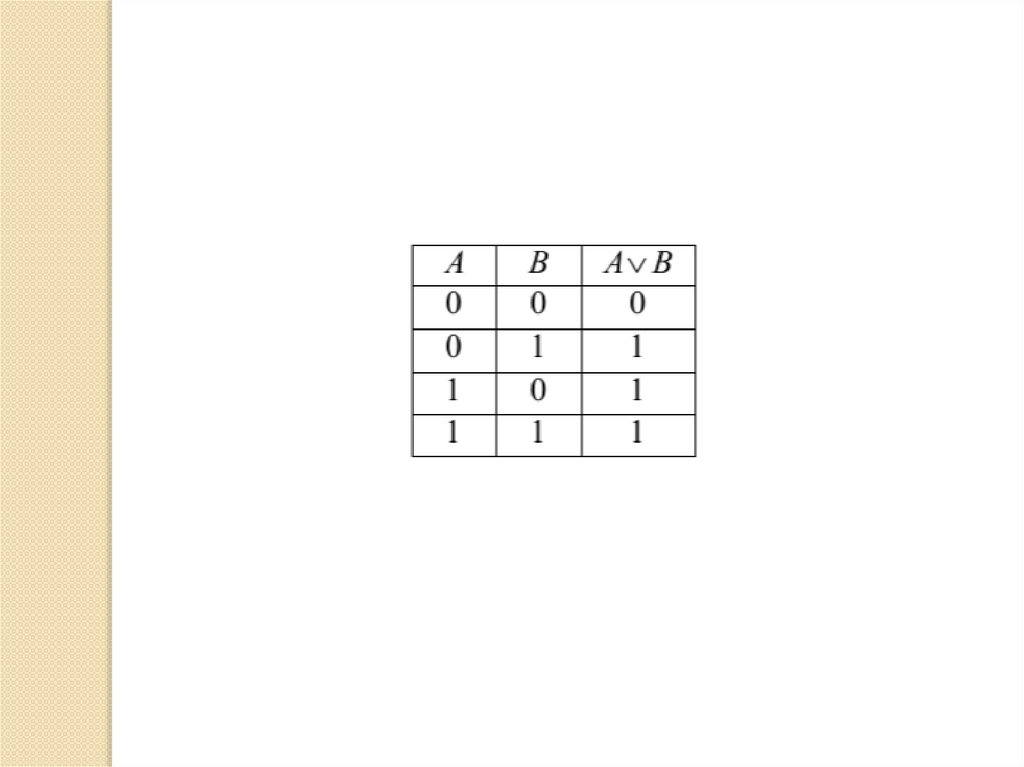
Дизъюнкция двух высказываний A и B — это
сложное логическое высказывание, которое ложно
только в случае ложности всех составляющих
высказываний, в противном случае оно истинно.
Таким образом, это высказывание считается
истинным, когда истинно хотя бы одно из
составляющих высказываний. Обозначается: . A∨В
Читается: «A или B»
13.
14.
Логические операцииВ математических доказательствах часто
пользуются сложными высказываниями,
образованными с помощью слов «если …, то
…». Здесь высказывание, расположенное
после слова «если», называется основанием
или
посылкой,
а
высказывание,
расположенное после слова «то», называется
следствием или заключением.
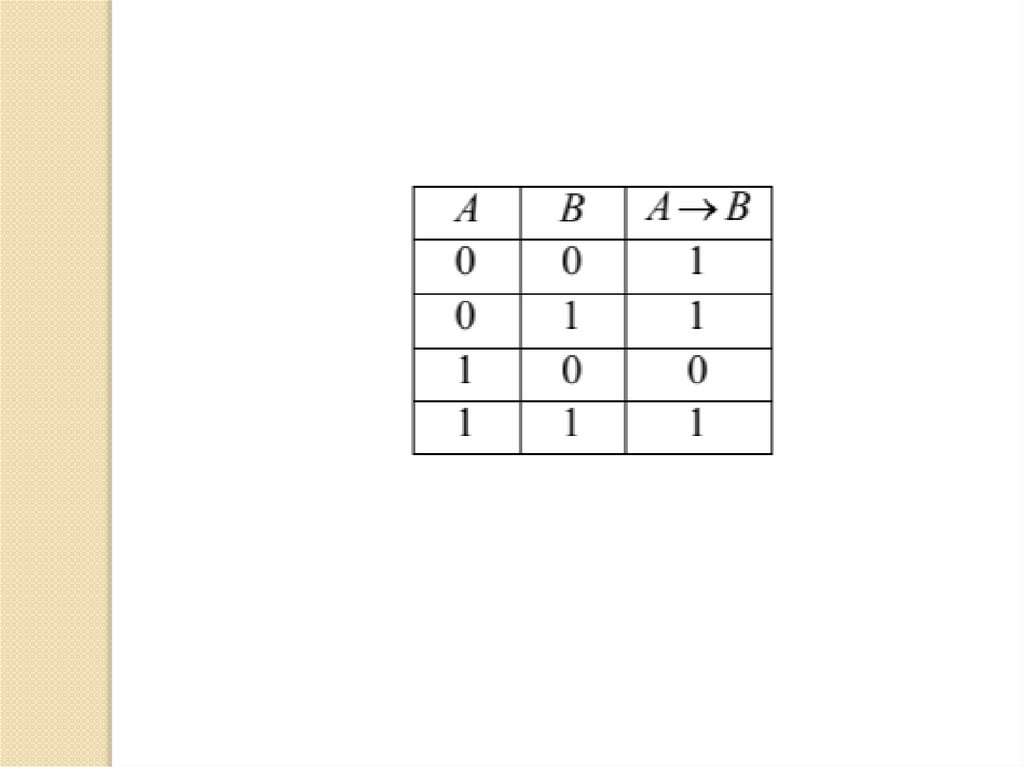
Импликацией двух высказываний A и B
называется высказывание, обозначаемое
символом A→В, , которое ложно тогда и
только тогда, когда A истинно, а B ложно.
Читается: «если A, то B» («A влечет B», «из A
следует B»).
15.
16.
Логические операцииОпределение импликации вынуждает
считать истинными такие предложения, как:
«Если 2×2=4, то Москва столица России»;
«Если 2×2=5, то 3×3=6».
Это связано с тем, что определениями
логических операций смысл составляющих
высказываний
не
учитывается,
они
рассматриваются как объекты, обладающие
единственным
свойством
—
быть
истинными, либо ложными.
17.
Истинность высказывания «Если 2×2=5, то 3×3=6»кажется парадоксальной.
Но объяснение этому, во-первых, следует искать в
том, что сами высказывания мало связаны между
собой, а во-вторых, в том, что использование
сослагательного наклонения несколько точнее
отражало бы смысл указанной импликации.
В самом деле, утверждение «Если бы 2×2=5, то
3×3=6» не кажется противоречивым, то есть
истинность нашей импликации означает, что
«3×3=6 не менее истинно, чем 2×2=5».
Операция импликации в русском языке является
самой «загадочной». Ей соответствую также
следующие речевые обороты: «из А следует В»; «А
имплицирует В»; «А достаточно для В»; «В
необходимо для А».
18.
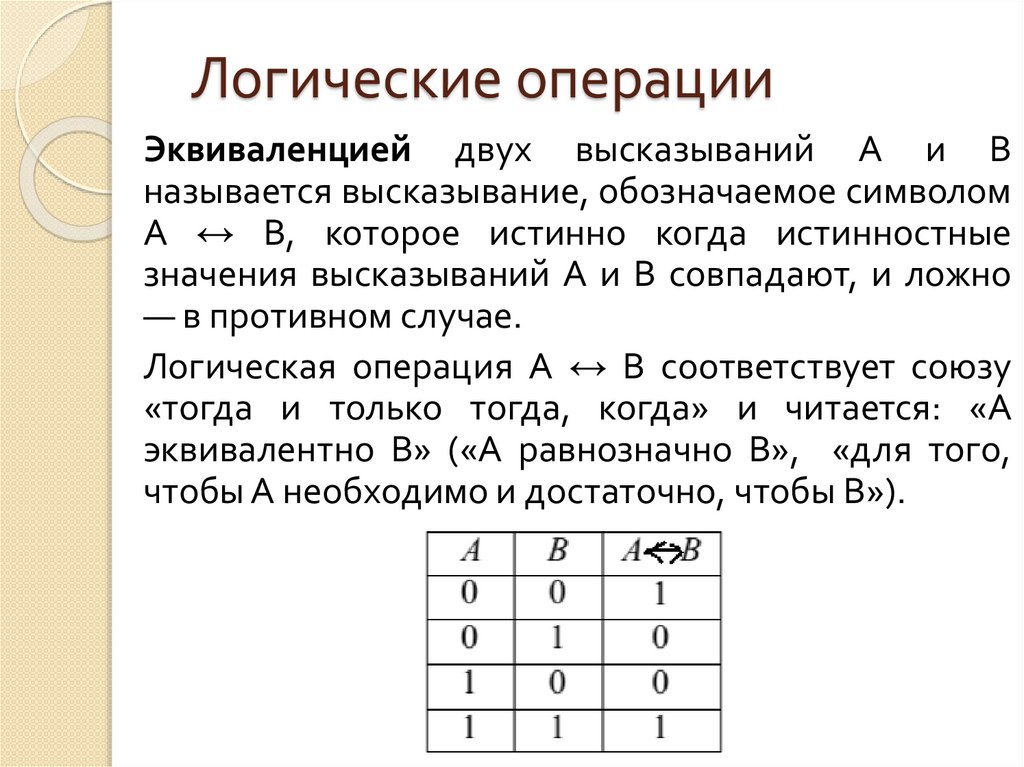
Логические операцииЭквиваленцией двух высказываний A и B
называется высказывание, обозначаемое символом
A ↔ В, которое истинно когда истинностные
значения высказываний A и B совпадают, и ложно
— в противном случае.
Логическая операция A ↔ B соответствует союзу
«тогда и только тогда, когда» и читается: «A
эквивалентно B» («A равнозначно B», «для того,
чтобы A необходимо и достаточно, чтобы B»).
19.
Когда мы говорим «A тогда и только тогда,когда B», то имеем в виду, что оба
предложения A и B одновременно истинны,
либо одновременно ложны.
Например, говоря: «Я поеду в Ленинград
тогда и только тогда, когда ты поедешь в
Киев», мы утверждаем, что: либо
произойдет и то и другое, либо ни того, ни
другого.
20.
Логические формулыВсякое сложное высказывание, которое может
быть получено из элементарных высказываний
посредством применения логических операций
отрицания,
конъюнкции,
дизъюнкции,
импликации
и
эквиваленции,
называется
логической формулой.
Представить логическими формулами следующие
высказывания:
а) «Сегодня суббота или воскресенье».
Решение. Пусть A — «сегодня суббота», а B —
«сегодня воскресенье»
AvB
б) «Если идет дождь, то крыши мокрые».
Решение. Пусть A — «идет дождь», а B — «крыши
мокрые». Тогда «если идет дождь, то крыши
мокрые» представимо формулой: . A→В
21.
«Что в лоб, что по лбу».«Если допоздна работаешь с
компьютером и при этом пьешь много
кофе, то утром просыпаешься в дурном
настроении или с головной болью».
22.
Логические формулыПусть даны высказывания:
A — «число 9 делится на 3»,
B — «число 10 делится на 3».
Требуется определить значения
истинности следующих высказываний:
1) B → A;
2) A → B ;
3) B →A.
23.
Логические формулыДля упрощения записи формул принят
ряд соглашений.
Скобки можно опускать, придерживаясь
следующего порядка действий:
конъюнкция выполняется раньше, чем все
остальные операции,
дизъюнкция выполняется раньше,
чем импликация и эквивалентность. Если
над формулой стоит знак отрицания, то
скобки тоже опускаются.
24.
Логические формулыТребуется построить таблицу
истинности для формулы:
F= (A ∧ B) ∧(B → A).
25.
Логические формулыФормула
называется ТОЖДЕСТВЕННО
ИСТИННОЙ (или ТАВТОЛОГИЕЙ), если она
принимает значение 1 при всех значениях
входящих в неё переменных.
Формула называется ТОЖДЕСТВЕННО
ЛОЖНОЙ (или ПРОТИВОРЕЧИЕМ), если
она принимает значение 0 при всех
значениях входящих в неё переменных.
26.
Логические формулыВыяснить, является ли следующая
формула тождественно истинной:
F = ((A → B) ∧ B) → A .
27.
Логические формулыДве формулы алгебры логики А и В называются
РАВНОСИЛЬНЫМИ,
если
они
принимают
одинаковые логические значения на любом наборе
входящих в формулы элементарных высказываний.
Равносильность формул будем обозначать знаком
, а запись А В означает, что формулы А и В
равносильны.
Между
понятиями
равносильности
и
эквивалентности существует следующая связь: если
формулы А и В равносильны, то формула А В –
тавтология, и обратно, если формула А В –
тавтология, то формулы А и В равносильны.
28.
Логические формулыСтандартный
метод
установления
равносильности двух формул:
1) по каждой формуле восстанавливается
таблица истинности;
2) полученные таблицы сравниваются по
каждому набору значений переменных.
29.
Логические формулыБудут ли формулы равносильными?
A ∨ B и A∧B

























 Математика
Математика








