Математическая модель технического объекта на макроуровне. Динамические системы с сосредоточенными параметрами. Тема 5

1.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ТЕХНИЧЕСКОГО ОБЪЕКТА НА МАКРОУРОВНЕ.
ДИНАМИЧЕСКИЕ СИСТЕМЫ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ
Динамическая модель технического объекта на макроуровне.
Математическая модель динамической системы с сосредоточенными
параметрами
Основные задачи анализа, решаемые при проектировании технических
систем.
Оценка физических свойств технической системы по спектру матрицы
Якоби. Характер переходных процессов в системе.
Качественный анализ динамической системы. Фазовый портрет,
обыкновенные и особые фазовые траектории (особые точки, предельные
циклы, сепаратрисы).
Техническая система, описываемая линейной системой двух
дифференциальных уравнений.
Примеры

2.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ДИНАМИЧЕСКАЯ МОДЕЛЬ ТЕХНИЧЕСКОГО ОБЪЕКТА НА МАКРОУРОВНЕ
На макроуровне осуществляют проектирование (или моделирование режима
работы) различных машин и механизмов (на микроуровне – отдельных деталей и
узлов машин).
Объекты моделирования на макроуровне рассматриваются как сложные
технические системы, состоящие из совокупности взаимодействующих
дискретных элементов. Задача проектирования таких объектов состоит в
определении оптимальных параметров и структуры исходя из заданного описания
внешней среды и технических требований к объекту.
Отдельный элемент макроуровня – это сложный объект (система) микроуровня.
Объекты моделирования на микроуровне описываются уравнениями в частных
производных, т. е. рассматриваются как динамические системы с
распределенными параметрами. Эти модели универсальны, дают наиболее
детальное описание физических свойств и позволяют решать любые задачи
анализа технического объекта. Однако они достаточно сложны даже для
отдельного элемента машины или механизма. Поэтому, если рассматривать
каждый элемент объекта макроуровня как сплошную среду, т.е. описывать его с
той же степенью детализации что и на микроуровне, то задача оптимизации
структуры и параметров макрообъекта становится практически неразрешимой.
Вместе с тем многие задачи проектирования успешно решаются с
использованием более простых (но более грубых) моделей макроуровня.

3.

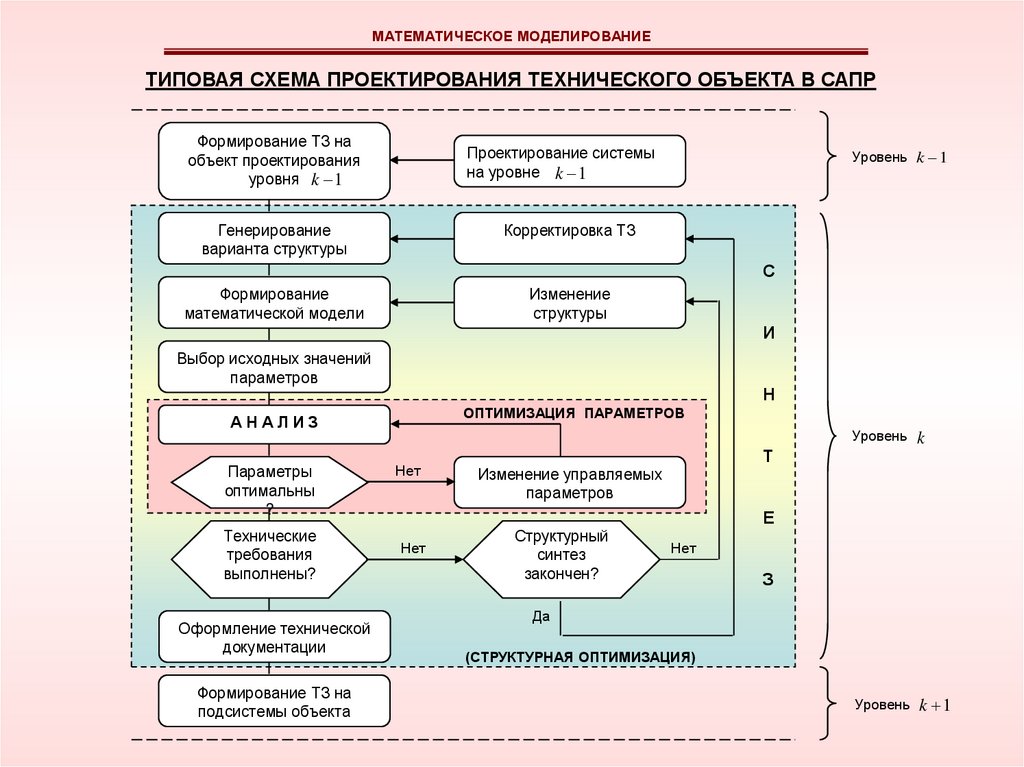
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ТИПОВАЯ СХЕМА ПРОЕКТИРОВАНИЯ ТЕХНИЧЕСКОГО ОБЪЕКТА В САПР
Формирование ТЗ на
объект проектирования
уровня k 1
Проектирование системы
на уровне k 1
Генерирование
варианта структуры
Уровень k 1
Корректировка ТЗ
С
Формирование
математической модели
Изменение
структуры
И
Выбор исходных значений
параметров
Н
ОПТИМИЗАЦИЯ ПАРАМЕТРОВ
АНАЛИЗ
Параметры
оптимальны
?
Технические
требования
выполнены?
Оформление технической
документации
Формирование ТЗ на
подсистемы объекта
Нет
Нет
Т
Изменение управляемых
параметров
Структурный
синтез
закончен?
Уровень k
Е
Нет
З
Да
(СТРУКТУРНАЯ ОПТИМИЗАЦИЯ)
Уровень k 1

4.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ДИНАМИЧЕСКАЯ МОДЕЛЬ ТЕХНИЧЕСКОГО ОБЪЕКТА НА МАКРОУРОВНЕ
Математическая модель макроуровня может быть построена огрублением
(осреднением) модели микроуровня. При этом отдельные подсистемы микроуровня
с непрерывно изменяющимися параметрами заменяются дискретными элементами
с постоянными параметрами. Постоянные параметры элементов макроуровня
получаются осреднением распределенных параметров микроуровня. Полученная в
результате осреднения система называется динамической системой с
сосредоточенными параметрами.
Другой распространенный метод построения математических моделей макроуровня
основан на составлении уравнений Лагранжа второго рода.
d T T
Qi
dt q i qi
i 1,2, ,n
где n - число степеней свободы,
q1 ,q2 , ,qn - обобщенные координаты,
q 1 ,q 2 , ,q n - обобщенные скорости,
Q1 ,Q2 , ,Qn - обобщенные силы,
T - кинетическая энергия рассматриваемой системы.
Этот подход отличается универсальностью, его можно применять к объектам любой
физической природы.

5.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
УРАВНЕНИЯ ЛАГРАНЖА 2-ГО РОДА
• Построение математической модели на основе уравнений Лагранжа второго рода
проводится в такой последовательности:
- определяется число n степеней свободы изучаемой материальной системы;
- выбирается система координат, и вводятся независимые обобщенные координаты
q1 ,q2 , ,qn в количестве равном числу степеней свободы;
- определяются обобщенные силы Q1 ,Q2 , ,Qn , соответствующие выбранным
обобщенным координатам;
- записывается выражение для вычисления кинетической энергии рассматриваемой
системы T через обобщенные скорости q 1 ,q 2 , ,q n и координаты q1 ,q2 , ,qn ;
- полученное выражение подставляется в уравнения
d T T
Qi
dt q i qi
i 1,2, ,n
и выполняются операции дифференцирования.
• В итоге получается система дифференциальных уравнений вида
fi q 1 ,q 2 , ,q n ,q 1 ,q 2 , ,q n ,q1 ,q2 , ,qn ,t 0
i 1,2, ,n
В эту систему входит n дифференциальных уравнений второго порядка. Данная
система может быть записана в виде эквивалентной системы первого порядка,
состоящей из 2n дифференциальных уравнений. Последняя система называется
нормальной системой уравнений.

6.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДИНАМИЧЕСКОЙ СИСТЕМЫ
Математическая модель динамической системы с сосредоточенными параметрами –
это система обыкновенных дифференциальных уравнений (в общем случае нелинейных)
(*)
где
du
f u , w,a ,t
dt
u - вектор фазовых переменных (фазовых координат), вектор состояния системы;
w - вектор внешних воздействий;
a - вектор параметров элементов технического объекта (внутренние параметры характеризуют
свойства или режим работы элементов, из которых состоит объект);
t - время.
Фазовые переменные – это физические величины, характеризующие состояние объекта в
процессе его функционирования. Такими величинами являются:
- в механических системах – силы и скорости;
- в пневмогидравлических системах – давления и расходы;
- в тепловых системах – тепловые потоки и температуры;
- в электрических системах – напряжения и токи.
Выходные параметры характеризуют свойства технического объекта, это показатели
(критерии) качества и эффективности технического объекта. Их подразделяют на следующие
группы: - назначения; - надежности; - безопасности; - стандартизации и унификации; экономические (экономного использования сырья, материалов, топлива, энергии, трудовых
ресурсов); - экологические (ограничения вредных воздействий продукции).
Выходные параметры объекта непосредственно не фигурируют в системе дифференциальных
уравнений (*). Они определяются по результатам решения этой системы уравнений.
Система дифференциальных уравнений (*) описывает динамические режимы функционирования
технического объекта.
Анализ этих режимов заключается в решении системы уравнений (*) (аналитически или
численно) и последующем определении выходных параметров объекта или иных характеристик.

7.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ОСНОВНЫЕ ЗАДАЧИ АНАЛИЗА, РЕШАЕМЫЕ ПРИ ПРОЕКТИРОВАНИИ ТЕХНИЧЕСКИХ СИСТЕМ
В вычислительном эксперименте при проектировании обычно задают некоторые стандартные
типовые (тестовые) воздействия на объект: ступенчатые, импульсные, гармонические, кусочнолинейные, экспоненциальные и т.п.
В зависимости от модельного режима, положенного в основу решения конкретной проектной
задачи, различают следующие виды анализа:
- анализ статических состояний (анализируется состояние покоя системы );
- анализ переходных процессов (анализируется процесс перехода из одного установившегося
режима функционирования в другой установившийся режим; установившееся состояние системы
достигается при неизменных характеристиках внешних воздействий);
- анализ устойчивости (изучается способность системы возвращаться в исходный или
близкий к нему установившийся режим при наложении различных возмущений);
- анализ стационарных режимов колебаний (изучается установившийся процесс
вынужденных колебаний при гармоническом внешнем воздействии после затухания свободных
колебаний);
- анализ частотных характеристик (определяются резонансные режимы
функционирования);
- анализ чувствительности (оценивается влияние изменения параметров объекта на
изменение целевой функции; из множества внутренних параметров объекта отбираются
управляемые параметры, которые наиболее эффективно влияют на функцию цели; эти
параметры используются на стадии оптимизации);
- анализ выходных процессов (по входным параметрам и описанию системы определяются
выходные параметры; многократное решение этой задачи и обработка результатов решения
методами регрессионного анализа позволяет построить упрощенную экспериментальную
факторную модель системы);
- анализ управляемости (изучается способность системы переходить из заданного начального
состояния в заданное конечное состояние под влиянием входного управляющего воздействия);
- статистический анализ (применяется на заключительном этапе проектирования для
анализа случайных воздействий внешней среды и случайного разброса параметров объекта,
обусловленного технологическим процессом изготовления).

8.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ОЦЕНКА ФИЗИЧЕСКИХ СВОЙСТВ ТЕХНИЧЕСКОЙ СИСТЕМЫ ПО СПЕКТРУ
МАТРИЦЫ ЯКОБИ. ХАРАКТЕР ПЕРЕХОДНЫХ ПРОЦЕССОВ В СИСТЕМЕ.
Качественный анализ математической модели макроуровня позволяет, не решая
систему дифференциальных уравнений оценить физические свойства технической
системы: ее устойчивость и характер переходных процессов.
Закон эволюции динамической системы (математической модели макроуровня)
описывается системой обыкновенных дифференциальных уравнений:
du
f u ,t
dt
u1 t
u u2 t
u t
n
Линейная система уравнений, A
f1 u1 ,u2 , ,un ,t
f f 2 u1 ,u2 , ,un ,t
f u ,u , ,u ,t
n 1 2
n
- матрица Якоби:
f1
u
1
f 2
A aik u1
f n
u1
,
du
Au
dt
f1
u2
f 2
u2
f n
u2
f1
un
f 2
un
f n
un

9.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ОЦЕНКА ФИЗИЧЕСКИХ СВОЙСТВ ТЕХНИЧЕСКОЙ СИСТЕМЫ ПО СПЕКТРУ
МАТРИЦЫ ЯКОБИ.
Спектром матрицы Якоби называется совокупность ее собственных значений
1 , 2 , , n
Собственными значениями квадратной матрицы A порядка n называются корни
ее характеристического уравнения
a11
a12
a22
a22
Pn x det A E
an1
an 2
a1n
a2 n
0
ann
Pn a0 n a1 n 1 an 1 an 0
В общем случае собственные значения являются комплексными числами
k Re k Im k k i k
Собственные значения определяются элементами матрицы Якоби, которые зависят
только от внутренних параметров (инерционных, упругих, диссипативных)
технической системы и не зависят от параметров внешних воздействий. Поэтому
матрица Якоби и ее спектр характеризуют внутренние физические свойства
системы.

10.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ХАРАКТЕР ПЕРЕХОДНЫХ ПРОЦЕССОВ В СИСТЕМЕ.
В спектре матрицы Якоби могут быть вещественные корни (в частности, нулевые),
комплексно-сопряженные и чисто мнимые:
k k , k 0, k k i k , k i k
Мнимые части собственных значений образуют дискретный спектр резонансных
частот технической системы. Для консервативных систем (без диссипативных
элементов) вещественные части всех собственных значений равны нулю, а мнимые
части образуют спектр собственных частот. При сильной диссипации (большие
коэффициенты внутреннего трения) количество резонансных частот может быть
меньше количества собственных частот, поскольку отдельные составляющие
переходных процессов могут стать апериодическими.
При совпадении частоты внешнего гармонического воздействия с одной из
резонансных частот системы, в ней может возникнуть резонансный режим работы.
Вещественным (отличным от нуля) корням соответствуют апериодический
нарастающий ( k 0 ) или затухающий ( k 0 ) переходный процесс. Если
собственное значение нулевое, то положение системы после снятия внешнего
воздействия сохраняется неизменным и система не возвращается в исходное
состояние.
Чисто мнимым корням соответствуют незатухающие гармонические колебания.
Комплексно-сопряженным корням с отличной от нуля вещественной частью
соответствуют колебательные процессы с нарастающей ( k 0 ) или
убывающей ( k 0 ) амплитудой.
Для устойчивости линейной системы необходимо и достаточно, чтобы
вещественные части всех собственных значений были отрицательны.
Система будет неустойчивой, если в спектре матрицы Якоби есть хотя бы одно
значение с положительной вещественной частью.

11.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ПЕРЕХОДНЫЙ ПРОЦЕСС, ОПРЕДЕЛЯЕМЫЙ ОТДЕЛЬНЫМ
СОБСТВЕННЫМ ЗНАЧЕНИЕМ МАТРИЦЫ ЯКОБИ
Вещественный корень k k
14
1,0
k 0
0,8
2,0
k 0
12
10
1,5
k 0
8
0,6
1,0
6
0,4
4
0,5
0,2
2
0,0
0,0
0
0
1
2
3
4
5
0
1
2
3
4
0
5
Комплексно-сопряженные корни
1
2
3
4
5
2
3
4
5
k k i k
1,5
1,0
k 0
k 0
10
1,0
k 0
0,5
5
0,0
0,5
0
0,0
-5
-0,5
-10
-1,0
-0,5
-1,0
-1,5
0
1
2
3
4
5
0
1
2
3
4
5
0
1

12.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
АЛГЕБРАИЧЕСКИЙ КРИТЕРИЙ РАУСА - ГУРВИЦА.
Критерий Рауса – Гурвица позволяет определить условия, когда все корни характеристического
уравнения будут иметь отрицательные вещественные части.
Для того чтобы все корни характеристического полинома имели отрицательные вещественные части,
необходимо и достаточно, чтобы все главные диагональные миноры матрицы Гурвица
Pn a0 n a1 n 1 an 1 an
a1
a
0
0
0
a3
a2
a1
0
a5
a4
a3
0
Pn an n an 1 n 1 a1 a0
0
0
0
an
an 1 an 3
a
an 2
n
0
an 1
0
0
an 5
an 4
an 3
0
0
0
0
a0
были положительными, т.е.
1 a1 0
2
a1
a0
a3
0
a2
a1
3 a0
0
a3
a2
a1
a5
a4 0 ,
a3
n 0
Матрица Гурвица формируется по следующему правилу: на главной диагонали стоят коэффициенты
полинома от a1 до an , индексы коэффициентов в строках увеличиваются на двойку, а в столбцах –
уменьшаются на единицу; вместо коэффициентов, индексы которых больнее чем n , и меньше, чем
нуль, ставятся нули.

13.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
АВТОНОМНЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ
Математическая модель динамической системы считается заданной, если введены
фазовые координаты u1 ,u2 , ,un системы, однозначно определяющие ее
состояние, и указан закон эволюции – закон изменения состояния во времени.
Закон эволюции динамической системы описывается системой обыкновенных
дифференциальных уравнений n - го порядка
du
f u ,t
dt
Система дифференциальных уравнений называется автономной, если
независимая переменная (время) не входит явно в систему. Автономные системы это системы не подверженные действии внешних сил переменных во времени.
Автономная система, приведенная к нормальной форме, имеет вид:
du
f u
dt
Любая нормальная система путем включения времени в состав фазовых
переменных может быть записана в виде автономной системы:
du
f u ,t
dt
un 1 t
du
dt f u ,un 1 ,
du
n 1 1
dt
При этом порядок системы возрастает на единицу.

14.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
КИНЕМАТИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ДИНАМИЧЕСКОЙ СИСТЕМЫ В ФАЗОВОМ ПРОСТРАНСТВЕ
Если рассматривать величины u1 ,u2 , ,un как координаты точки в n - мерном
пространстве, то получается наглядное представление состояния динамической
системы в виде этой точки. Эту точку называют фазовой точкой, а пространство
состояний – фазовым пространством динамической системы. Изменению
состояний системы во времени отвечает движение фазовой точки вдоль некоторой
линии, называемой фазовой траекторией. Семейство фазовых траекторий
образуют фазовый портрет динамической системы.
Механической системе с k степенями свободы соответствует фазовое пространство
размерности в два раза большей
. Точкиnфазового
пространства, в которых
2k
правая часть системы обращается в нуль, т.е.
f1 u1 ,u2 , ,un 0
f 2 u1 ,u2 , ,un 0
f n u1 ,u2 , ,un 0
называются особыми точками (или точками покоя) системы.
Особые точки соответствуют стационарным состояниям технических систем.
Кроме точек покоя среди фазовых траекторий выделяются еще замкнутые гладкие
кривые, называемые циклами.
Всякая фазовая траектория динамической системы (с непрерывно
дифференцируемой правой частью) принадлежит к одному из трех типов: гладкая
кривая без самопересечений, цикл или точка.
Особым точкам соответствует положение равновесия системы, циклам –
периодические (колебательные) режимы движения.

15.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
КАЧЕСТВЕННЫЙ АНАЛИЗ АВТОНОМНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ
Рассмотрим автономную динамическую систему (с непрерывно дифференцируемой
правой частью) при n 2 :
du1
f1 u1 ,u2
dt
f 2 u1 ,u2 0
Эти точки (особые точки, точки покоя, положения равновесия технической системы)
,
классифицируются в зависимости от поведения
фазовых траекторий в малых
окрестностях этих точек. Данное обстоятельство позволяет ограничиться анализом
линеаризованных уравнений.
.
Пусть u10 , u20 - исследуемое состояние равновесия системы, т.е.
f1 u10 ,u20 0
(*)
Положениями равновесия системы являются точки фазовой плоскости, в которых
правые части уравнений обращаются в нуль:
f1 u1 ,u2 0
du2
f 2 u1 ,u2
dt
f 2 u10 ,u20 0
Разлагая правые части системы (*) в ряды Тейлора в окрестности точки равновесия,
получим
du1
f1 u10 ,u20
f1 u10 ,u20
0 0
0
f1 u1 ,u2
u1 u1
u2 u20
dt
u1
u2
du2
f 2 u10 ,u20
f 2 u10 ,u20
0 0
0
f 2 u1 ,u2
u1 u1
u2 u20
dt
u1
u2

16.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
КАЧЕСТВЕННЫЙ АНАЛИЗ АВТОНОМНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ
Переходя к новым переменным (перенося начало координат в особую точку)
x1 u1 u10
x2 u2 u20
и вводя обозначения (для элементов матрицы Якоби)
f1 u10 ,u20
a11 ,
u1
f 2 u10 ,u20
a12
u1
получим линейную автономную систему:
f 2 u10 ,u20
a21 ,
u1
f 2 u10 ,u20
a22
u2
dx1
dt a11x1 a12 x2
dx
2 a21x1 a22 x2
dt
Характер равновесия системы (его устойчивость, асимптотическую
устойчивость, неустойчивость) можно, установить, не решая системы, на основе
анализа собственных значений матрицы Якоби.
Пусть 1 , 2 - спектр матрицы Якоби, т.е. корни квадратного уравнения
a11
a21
a12
0
a22
В зависимости от характера значений 1 , 2 особая точка называется: седлом,
центром, узлом (устойчивым или неустойчивым ), фокусом (устойчивым или
неустойчивым ). Если одно или оба значения k обращается в нуль, особые точки
составляют целую прямую, или всю плоскость.

17.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ФАЗОВЫЙ ПОРТРЕТ ДИНАМИЧЕСКОЙ СИСТЕМЫ В ОКРЕСТНОСТИ
ПОЛОЖЕНИЯ РАВНОВЕСИЯ
2.158
3
T1
УЗЕЛ
3
2
3
T1
2
3
T2
3
T2
3
T3
3
T4
3
T3
1
0
1
3
T4
3
T5
0
3
T5
3
T6
СЕДЛО
2
0
3
T6
1
3
T7
3
T8
2
1
0
2.158
3
4
2
0
2
2
2
2
2
2
2
3 T1
T2
T3
T4
T5
T6
0
4
3
Собственные значения действительные числа одного знака.
k 0 - неустойчивый узел
k 0 - устойчивый узел
2
2
2
2.2
1
0
1
2
2
2
2
2
2
2
2
2
2.2
T1 T2 T3 T4 T5 T6 T7 T8 0
Собственные значения действительные числа разных знаков.
Особая точка – неустойчива.
k Re k Im k k i k

18.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ФАЗОВЫЙ ПОРТРЕТ ДИНАМИЧЕСКОЙ СИСТЕМЫ В ОКРЕСТНОСТИ
ПОЛОЖЕНИЯ РАВНОВЕСИЯ
1.838
ФОКУС
2
1.512
3
T1
3
T2
3
T1
3
T2
1
3
T3
3
T4
3
T4
0
0
3
T5
3
T6
1
0
1.838
1
3
T3
3
T5
3
T6
ЦЕНТР
2
1
0
2
2
2.2
1
0
1
2
2
2
2
2
2
T1 T2 T3 T4 T5 T6 0
1.511
2
Собственные значения - комплексно k k i k
сопряженные
k 0 - неустойчивый фокус
k 0 - устойчивый фокус (особая
точка асимптотически устойчива).
2.2
2
2
2.2
1
0
1
2
2
2
2
2
2
T1 T2 T3 T4 T5 T6 0
2
2.2
Собственные значения - комплексносопряженные, чисто мнимые k i k
Особая точка – устойчива, но не
асимптотически устойчива.

19.

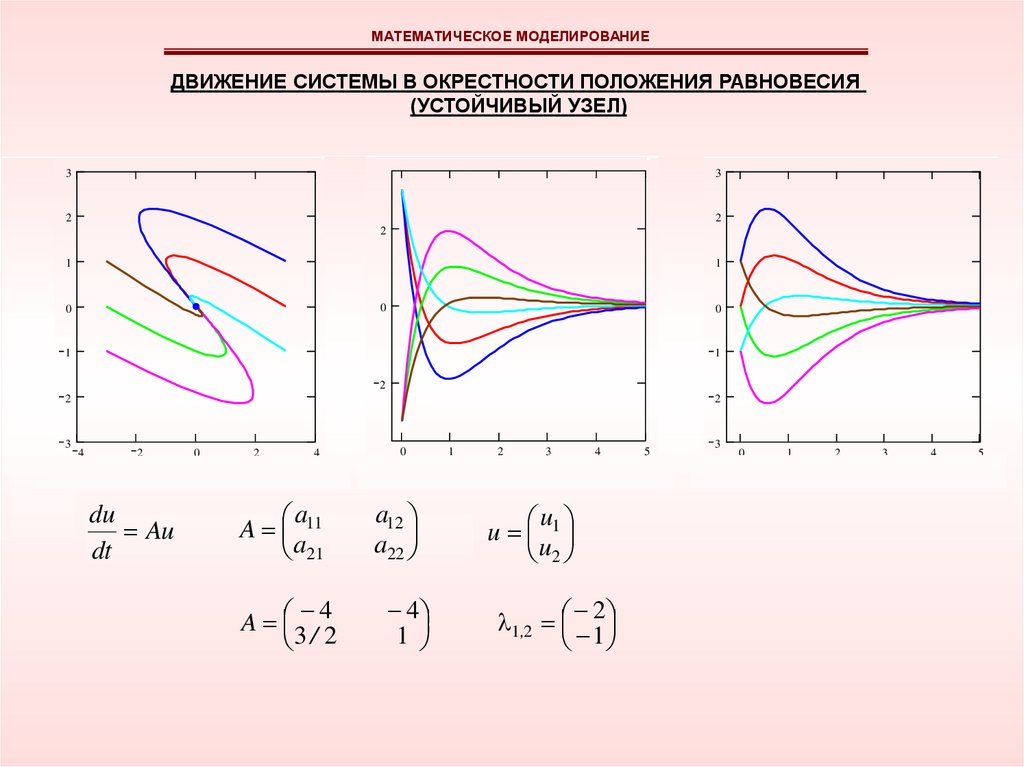
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ДВИЖЕНИЕ СИСТЕМЫ В ОКРЕСТНОСТИ ПОЛОЖЕНИЯ РАВНОВЕСИЯ
(УСТОЙЧИВЫЙ УЗЕЛ)
3
2.158
3 3
T1 T1 2
3
T2 T2 3
1
3
T3 T3 3
3
T5 T5 3
1
3
T6 T6 3
1
0
2
2.158
3
2.158
3
3
T1 2
2
T1 3
T1
2
3 2
T2 2
T2 3
T2 1
3
T3 2
1
T3 3
T3
3
0
T4 2
T4 3 0
0
T4
3
T5 2
T5 3
T5 1
3
1
T6 2
T6 3
T6 2
0
2
0
0
2
1
0
2
3.5
2
3
T4 T4 30
0
3
3
3.5
3
0 4
1
2
54
2
0 3
24
1 2 1 2 1 2 1 2 1 2 1 2
T1
3 T1
T2 T2 T3 T3 T4 T4 T5 T5 T6 T6 x 0 3
du
Au
dt
3
3
T1
3
T1
2
3
T2
3
T3
3
T4
T2
1
T3
T4
0
3
T5
3
T6
0
2.158
2
0
2
4
1
2
3
4
5
0 2 2 1 2 2 2 2 3 2 4
5
1 T2 1 T3 1 T4 1 T5 1 T6 1 0
0.2T1
5
T1 T2
T3
T4
T5
T6
x1
1
1
1
1
1
T1 T2 T3 T4 T5 T6 x
4
30
a
A 11
a21
a12
a22
u
u 1
u2
A 4
3 / 2
4
1
1,2 2
1
T5
1
T6
0
2
3
0
1
2
3
4
0.3 T1 1 T2 1 T3 1 T4 1 T5 1 T6 1 x
5
5

20.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ДВИЖЕНИЕ СИСТЕМЫ В ОКРЕСТНОСТИ ПОЛОЖЕНИЯ РАВНОВЕСИЯ
(НЕУСТОЙЧИВЫЙ УЗЕЛ)
0.262
3
1
3
T1
3
2
3
T2
0.2
2
3
T1
0.15
T1
3 0.2
2
T2
3
T2
T2
3
2 0.1
T3
3 0.05
T3
T3
3 0.1
2
T4
3
T4
T4
0.05
3
2
T5
3
T5
T5
3
0 2
T6
0
3
T6
0
T6
3
2
T7
T7
3
T7
0.05
0
0.1
0
0
3
2
T8
3
T8
T8
0.1
3
0.05
T9
2
3
T9
0.2
T9
3
T10
2
T10 0.15 3
T10
0.2
3 0.05 3
3
T3
3
4
3
T4
3
5
3
T5
3
6
0T6 3
3
7
3
T7
0
3
8
0.1
0
0.1
3
T8
0.05
3
3
T9
9
3
10
3
T10
0.1
3
T1
0.2
3
T1
T1
3
T2
T2
3 0.05
T3
T3
3
T4
T4
3
T5
T5
3
T6
3
T7
T7
0
0
3
T8
3
T9
T8
0.05
T9
3
T10
0.262 0.3
0
0.3 0.2
0.1
0.2
0.1
0
0.1
0.2
0.2
0.1
0
0.2
0.5
1
1.5 0.1
0
0.5
1
1.5
2
2
2
2 0.5
2
2
2 1 2
2
0 2
1.5
2 0.22
1 0.22 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2
T1 0.1
T2 T3
T4
T5
T6
T7
01 T8 1 T9 1T10 1
1
1
1
1
1
1
1.9
1
T7 T9
0 T8 T10
T9 T10
T1 T2 T1 T3 T2 T4 T3 T5 T4 T6 T5 T7 T6 x T8
T1 T2 1 T3 1 T4 1 T5 1 T6 1 T7 1 x T8 1 T9 1 T10 1
T1 T2 T3 T4 T5 T6 T7 x T8 T9 T10
du
Au
dt
T6
0
a
A 11
a21
a12
a22
u
u 1
u2
A 0
1
1
2.1
1,2 0.73
1.37
T1
0
0.5
1
1.5
0.1 T1 1 T2 1 T3 1 T4 1 T5 1 T6 1 T7 1 x T8 1 T9 1 T10 1
1.9

21.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ДВИЖЕНИЕ СИСТЕМЫ В ОКРЕСТНОСТИ ПОЛОЖЕНИЯ РАВНОВЕСИЯ (СЕДЛО)
2
3
T1 3
T1
3
T2 3
T2
3
T3 3
T3
3
T4 3
T4
3
T5 3
T5
3
T6 3
T6
3
T7 3
T7
3
T8 3
T8
2
2
2
1
1
0
0
11
0
0
2
2
2
2
2
2.2
3
T1
32
T1
T1
3
T1
3
T2
3
T2
3
T3
32
T2
T2
1
32
T3
T3
3
T4
32
T4
T4
3
T5
32
0T5
T5
3
T6
32
T6
T6
3
T6
3
T7
32
T7
T7
3
T7
3
T8
1 32
T8
T8
0
00
2
1
0
1
2
0
0.5
1
1.5
2.2 T1 2 T2 2 T3 2 T4 2 T5 2 T6 2 T7 2 T8 2 0
2.2
1
1
1
1
1
1
1
1
T1 T2 T3 T4 T5 T6 T7 T8 x
du
Au
dt
2
2 2
2
1
1
3
T3
2
2
T1
2
T2
2
T3
1
2
T4
3
T4
3
T5
00
1
1
3
T8
2
T5
0
2
T6
2
T7
2
T8
1
0
0
2
2
2.2
0.5
00.5
1 11
2
1.5
01
1.5
2
2 11 2 11 2 11 2 11 2 11 2 11 2 11
11
1.6
T1 0.2
T2T1
T2
T3
T4
T5
T6
T7
T1 T3
T2 T4
T3 T5
T4 T6
T5 T7
T6 T8
T7 0 T8
T8 xx
0
a
A 11
a21
a12
a22
u
u 1
u2
A 2
1
1
3
1,2
2
0
0.5
1
1.5
0.1 T1 1 T2 1 T3 1 T4 1 T5 1 T6 1 T7 1 T8 1 x
1.6
1 29 2.193
3.193
2

22.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ДВИЖЕНИЕ СИСТЕМЫ В ОКРЕСТНОСТИ ПОЛОЖЕНИЯ РАВНОВЕСИЯ
(УСТОЙЧИВЫЙ ФОКУС)
2
1.838
2
2.3
2
2
3
T1
1
3
T2
1
3
T3
0 T4 3
0
3
T5
3
1 T6
1
0
2 1.838
2
2
T1
2
T1
2
T1
2
T2
2
1 T2
2
1 T2
2
T3
2
T3
2
T3
2
T4
2
0 T4
0 T4 2
2
T5
2
T5
2
T5
2
T6
1 T6 2
1 T6 2
0
0
0
2
2
2
1
1 0
0 1
1 2
2
2 2 2 2 2 2 2 2 2 2
2
2.2
T1 T2 T1 T3 T2 T4 T3 T5 T4 T6 T5 0 T6 0
du
Au
dt
2.3
20
2.2
2.1
2
2
1
0
1
2
2
3
T1
3
T1
3
T2
1 T2 3
3
T3
3
T3
3
T4
3
0 T4
3
T5
3
T5
3
T6
3
1 T6
1
0
1
0
0
2
2.1
65
10
210
321
432
543
654
1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0.4 1
6
T1
T2
T1
T3
T2
T4
T3
T5
T4
T6
T5
x
T6
x
T1 T2 T3 T4 T5 T6 x
a
A 11
a21
a12
a22
u
u 1
u2
A 0
3
2
1
1,2
1 i 23
2
2
2
06
0.4
10
21
32
43
54
65
1
1
1 1 1 1 1 1 1 1 1 1
6
T1
T2
T3
T4
T5
T6
x
T1 T2 T3 T4 T5 T6 x

23.

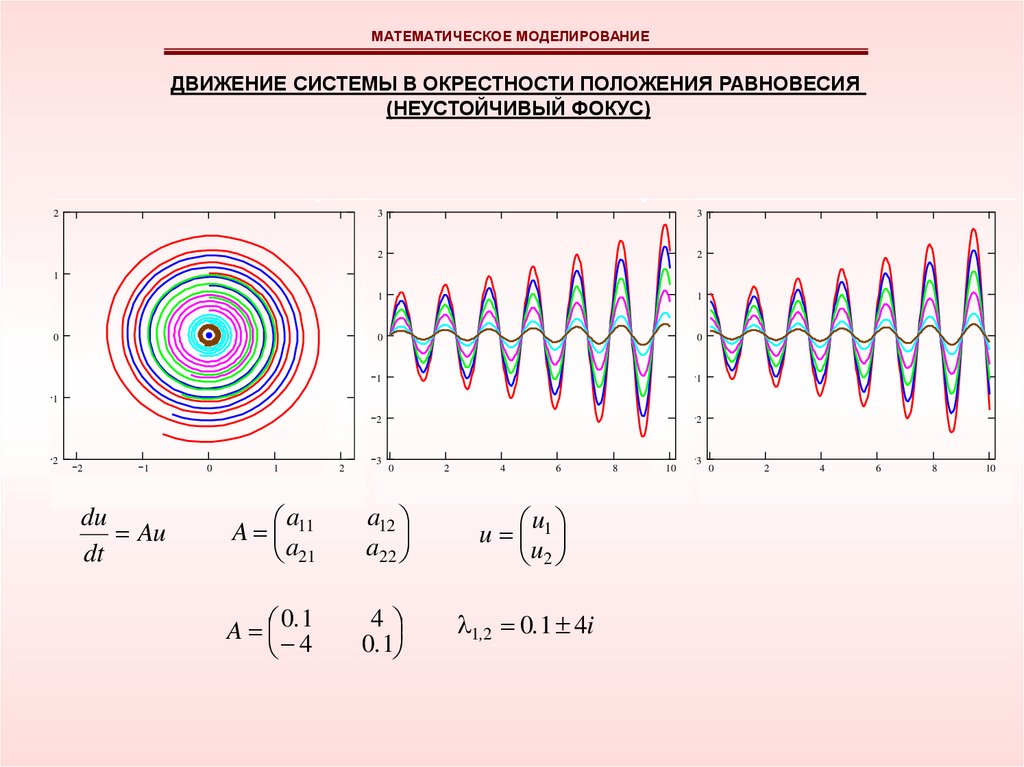
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ДВИЖЕНИЕ СИСТЕМЫ В ОКРЕСТНОСТИ ПОЛОЖЕНИЯ РАВНОВЕСИЯ
(НЕУСТОЙЧИВЫЙ ФОКУС)
3
1.6
2
2.668
3
2 T1
3
T2
1
2
X1
3
T6
3
X3
3
X4
0
2
22
4 1
6
0
8
1 10
2 1 2 1 2 1 2 1 2
2
X1
2.2 1 X2 1 T1
X3 T2
X4 T3
X5 T4
X6 T5
x T6 0
du
Au
dt
2
1
0
3
X5
2
X5
1
3
3
X2
1
2
X4
0
2 0
3 1.731
0
3
X1
2
2
X3
3
T5
1
2.567
2
X2
1
3
T3
3
0 T4
3
2
X6
1
3
X6
1
0
2
0
2
2.468
2
3
2.37
10
3
2.2
0
0.1
2
4
6
8
1
1
1
1
1
1
X1 X2 X3 X4 X5 X6 x
a
A 11
a21
a12
a22
u
u 1
u2
A 0.1
4
4
0.1
1,2 0.1 4i
10.2
0
0.1
2
4
6
8
1
1
1
1
1
1
X1 X2 X3 X4 X5 X6 x
10
10.2

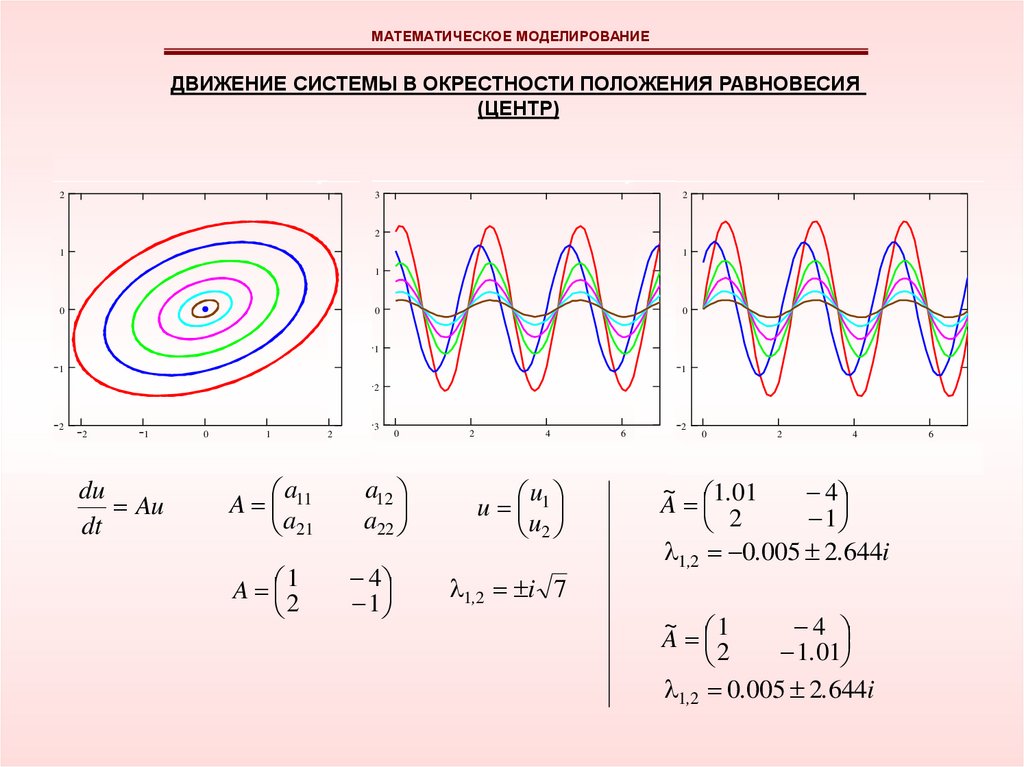
24.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ДВИЖЕНИЕ СИСТЕМЫ В ОКРЕСТНОСТИ ПОЛОЖЕНИЯ РАВНОВЕСИЯ
(ЦЕНТР)
2
1.512
3
1
3
T1
3
2
1 3
T2
3
3
3
T3
3
4
0 3
T4
3
5
3
T5
3
6
3
T6
1
2
2.137
2
3
T1
3
T2
1
3
T3
3
T4
0
3
T5
3
T6
1
0
0
1.511
2
0
2
40
16
1 2 1 2 1 2 1 2 1 2
2
2.2 T1 1 T2
T1 T3
T2 T4
T3 T5
T4 T6
T5 x T6 0
2
2
1
du
Au
dt
2
T1
1
2
T2
2
T3
0 2
T4
2
T5
2
1T6
0
1.512
2
3
T2
1
3
T3
0 3
T4
3
T5
1
3
T6
3
2
3
T1
2 3
T1
3
T2
1
2
T1
2
T2
1
3
T3
3
T4
0
2
T3
2
T4
0
3
T5
3
T6
1
2
T5
2
T6
1
0
02
2 2.138
2
2
2.2
3
0
1.511
1
0
1
2
0 2
2
4
6
2 0 2
2
2 2 2
2
4
6
1
T4
T5
T6
01
1
1
1
1
0.3T1 T2 T1 T3
7
T2 1 T3 1 T4 1 T5 1 T6 1 x 1
T1 T2 T3 T4 T5 T6 x
a
A 11
a21
a12
a22
u
u 1
u2
A 1
2
4
1
1,2 i 7
2
0
0.3
2
4
1
1
1
1
1
1
T1 T2 T3 T4 T5 T6 x
~
4
A 1.01
1
2
1,2 0.005 2.644i
~
4
A 1
1.01
2
1,2 0.005 2.644i
6
7

25.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ТИПЫ ОСОБЫХ ТОЧЕК ЛИНЕЙНОЙ АВТОНОМНОЙ СИСТЕМЫ
Таким образом, в зависимости от величины и знака корней характеристического
уравнения линейная система с невырожденной матрицей
du1
dt a11u1 a12u2
du2 a21u1 a22u2
dt
может иметь шесть различных типов положения равновесия:
седло; положение равновесия неустойчиво; переходный процесс представляет собой
апериодический уход от неустойчивого состояния равновесия;
устойчивый узел; при малых отклонениях от положения равновесия в линейной
системе имеет место апериодический затухающий переходный процесс; состояние
равновесия асимптотически устойчиво;
неустойчивый узел; при отклонении от положения равновесия имеет место
апериодический нарастающий переходный процесс;
устойчивый фокус; переходный процесс имеет характер затухающих колебаний;
состояние равновесия асимптотически устойчиво;
неустойчивый фокус; переходный процесс имеет характер нарастающих колебаний;
состояние равновесия неустойчиво;
центр; при малых начальных отклонениях от положения равновесия в системе
возникают периодические колебания, амплитуда которых определяется начальными
условиями; состояние равновесия устойчиво, но асимптотической устойчивости нет.

26.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
?
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ.
1. Что характерно для моделей технических объектов на макроуровне. Какие способы
построения математических моделей макроуровня вы знаете?
2. Что представляет собой математическая модель системы с сосредоточенными параметрами?
Какие переменные величины она объединяет и как используется на практике?
3. Перечислите основные задачи, решаемые с использованием моделей макроуровня; дайте
краткую характеристику этим задачам.
4. Какие типовые элементы и подсистемы выделяются при построении моделей макроуровня?
Раскройте содержание этого вопроса на конкретном примере.
5. Что такое эквивалентные схемы и как они используются на практике?
6. Приведите математические модели инерционного элемента для различных типов систем.
Какие переменные и параметры входят в эти модели? В чем проявляется аналогия между
математическими моделями?
7. Приведите математические модели диссипативного элемента для различных типов систем.
Какие переменные и параметры входят в эти модели? В чем проявляется аналогия между
математическими моделями?
8. Приведите математические модели упругого элемента для различных типов систем. Какие
переменные и параметры входят в эти модели? В чем проявляется аналогия между
математическими моделями?
9. Что можно сказать о качественных свойствах моделируемой системы, вычислив спектр
матрицы Якоби?
10. Что такое фазовый портрет динамической системы? Чем могут отличаться различные
фазовые траектории?
11. Укажите основные типы точек покоя динамической системы на плоскости. Как выглядит
фазовый портрет в окрестности этих точек?
12. Как выглядит движение системы в окрестности точки покоя для различных типов точек
покоя? Как связан этот вопрос с корнями характеристического уравнения?
Литература: [3], [1], [8], [9], [2].