Радикальные оси

1.

Радикальные оси
Подготовили: Бучацкая М., Беджанов А.

2.

Что такое радикальная ось?
Для двух неконцентрических окружностей геометрическое место
точек, для которых степени относительно данных окружностей
равны, называется радикальной осью данных окружностей.

3.

Некоторые факты про радикальные оси
➢ Если окружности пересекаются в двух точках, то радикальная
ось содержит их общую хорду, а если окружности касаются —
общую внутреннюю касательную.
➢ Пусть к двум окружностям проведены две внешние и две
внутренние касательные. Тогда середины отрезков,
соединяющих точки касания, лежат на радикальной оси.

4.

Некоторые факты про радикальные оси
➢ Рассмотрим три не концентрические окружности. Тогда три
прямые, являющиеся радикальными осями пар данных
окружностей пересекаются в одной точке или параллельны
или совпадают. Из этого так же следует, что прямые,
содержащие общие хорды пар трех попарно
пересекающихся окружностей пересекаются в одной точке
или параллельны или совпадают.

5.

Важный факт
Для двух неконцентрических окружностей радикальная ось
является прямой перпендикулярной линии центров данных
окружностей.

6.

Задача
Через вершины B и C треугольника
ABC провели перпендикулярно
прямой BC прямые b и c
соответственно. Серединные
перпендикуляры к сторонам AC и AB
пересекают прямые b и c в точках P и
Q соответственно. Докажите, что
прямая PQ перпендикулярна медиане
AD треугольника ABC.

7.

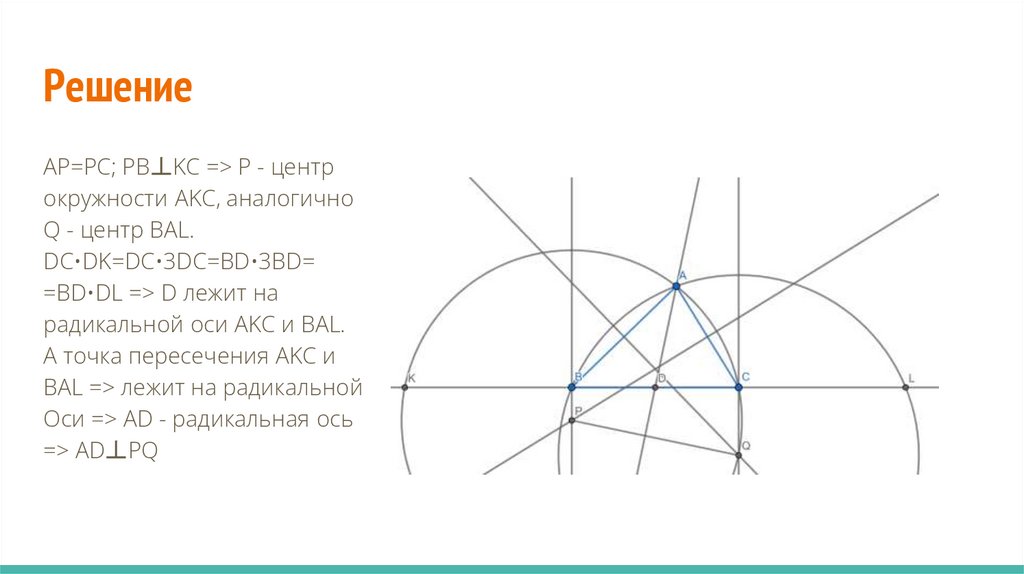
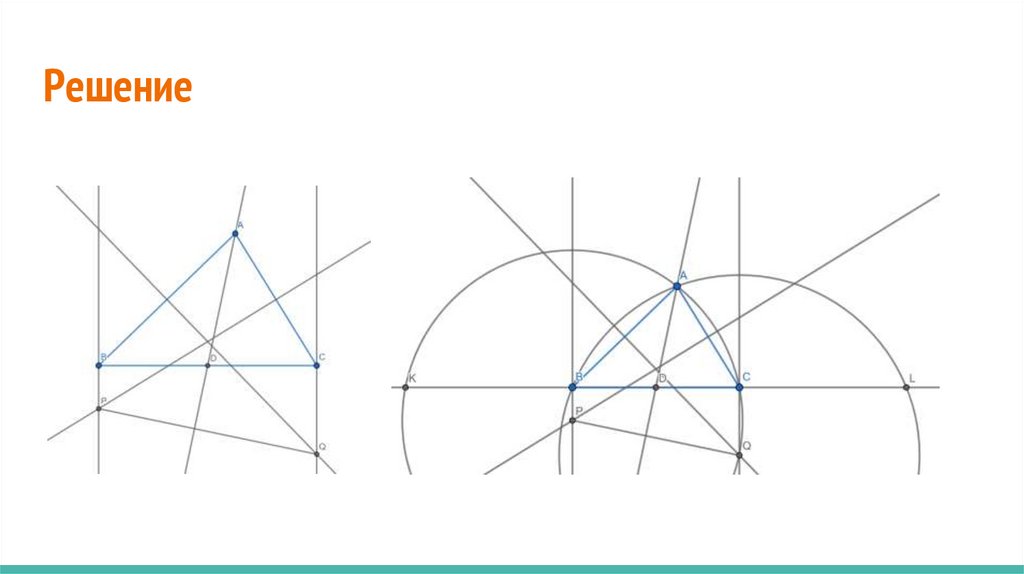
Решение
AP=PC; PB丄KC => P - центр
окружности AKC, аналогично
Q - центр BAL.
DC•DK=DC•3DC=BD•3BD=
=BD•DL => D лежит на
радикальной оси AKC и BAL.
A точка пересечения AKC и
BAL => лежит на радикальной
Оси => AD - радикальная ось
=> AD丄PQ

8.

Решение