Похожие презентации:
Геоинформационные технологии пространственного анализа
1.
ГЕОИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИПРОСТРАНСТВЕННОГО АНАЛИЗА
2 курс, весенний семестр 2023 г.
Преподаватель:
• Лозбенев Николай Игоревич
Информационная поддержка:
• http://landscapeedu.ru - лекционные и практические материалы, задания,
статьи, ссылки на тематические сайты
Занятия:
• вторник 4-5 пары, 14:55-18:15, ауд. 2017
• лекции - 26 часов, практические - 26 часов
• самостоятельно 20 часов
Задания:
• создание инвентаризационной ГИС (согласованные базовые слои)
• реферат статьи 2018-23 года из каталога ELSEVIER
• индивидуальный проект (тематическое картографирование)
Проверка знаний:
• практические задания (80%), экзамен (20%) + активная работа
• оценка выставляется по сумме набранных баллов
2.
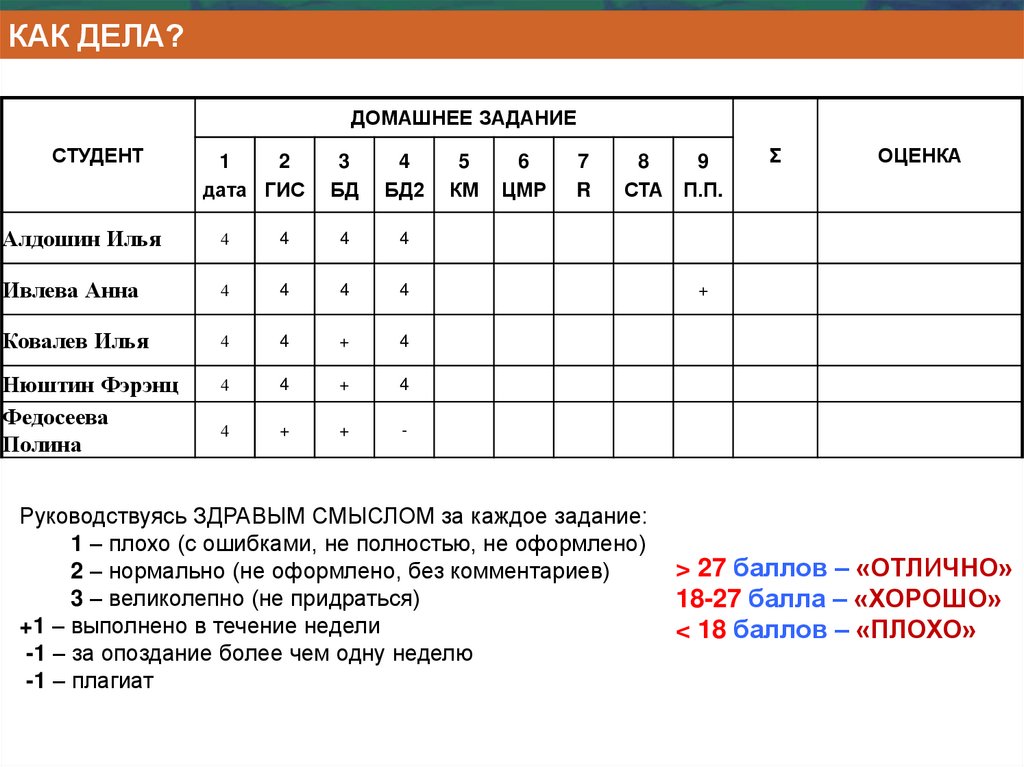
КАК ДЕЛА?ДОМАШНЕЕ ЗАДАНИЕ
СТУДЕНТ
1
2
дата ГИС
3
БД
4
БД2
Алдошин Илья
4
4
4
4
Ивлева Анна
4
4
4
4
Ковалев Илья
4
4
+
4
Нюштин Фэрэнц
Федосеева
Полина
4
4
+
4
4
+
+
-
5
КМ
6
ЦМР
7
R
8
9
СТА П.П.
Руководствуясь ЗДРАВЫМ СМЫСЛОМ за каждое задание:
1 – плохо (с ошибками, не полностью, не оформлено)
2 – нормально (не оформлено, без комментариев)
3 – великолепно (не придраться)
+1 – выполнено в течение недели
-1 – за опоздание более чем одну неделю
-1 – плагиат
Σ
ОЦЕНКА
+
> 27 баллов – «ОТЛИЧНО»
18-27 балла – «ХОРОШО»
< 18 баллов – «ПЛОХО»
3.
ДОКЛАД ПО СТАТЬЕСтудент
Статья
Алдошин Илья
Effect of surface temperature on soil moisture retrieval using CYGNSS
Ивлева Анна
Reflections and speculations on the progress in Geographic Information Systems
(GIS): a geographic perspective
Ковалев Илья
Using geoinformatics to assess tourist dispersal at the state level
Нюштин Фэрэнц
Forecasting vegetation dynamics in an open ecosystem by integrating deep
learning and environmental variables
Федосеева Полина
Mapping place values: 10 lessons from two decades of public participation GIS
empirical research
Структура презентации по статье:
1. Авторы, место работы, статус журнала
2. Актуальность, цель, задачи исследования
3. Регион исследования (если применимо)
4. Использованные методы, модели, данные с разъяснением сути
5. Основные результаты
6. Критический анализ результатов: их качество, реалистичность и
т.п. (раздел «discussion»)
Требования к докладу:
1. От 10 до 20 минут + вопросы по 1 от каждого студента
2. Подписи в таблица и рисунка должны быть осмысленно
переведены на русский
4.
РАСПИСАНИЕ 2023ВВОДНАЯ. ЦЕЛИ, ЗАДАЧИ и СОДЕРЖАНИЕ КУРСА
07.02
Источники пространственных данных: карты, каталоги космических снимков, базы данных
полевых наблюдений, данные реанализов и др.
ДЗ
+ Наука о ландшафте и ГИС. Главные понятия пространственного анализа*.
14.02,
21.02
Создание инвентаризационной ГИС с набором базовых слоев: подготовка и привязка
топооснов, снимков, векторизация, атрибуты, топологическая коррекция, буферные и
оверлейные операции, интеграция данных глобального позиционирования.
ДЗ
Персональный проект.
28.03
07.03
Базы данных. Структура БД, таблицы, формы, отчёты, запросы в среде Access.
Использование БД в составе ГИС.
ДЗ
ДЗ
14.03
Геостатистика: вариография и интерполяция. ЦМР, поля и резервуары
ДЗ
21.03
Морфометрический анализ ЦМР: карты свойств и элементов рельефа
ДЗ
28.03
Морфометрический анализ ЦМР: карты расчлененности и сложности рельефа
ДЗ
04.04
Индикационное цифровое картографирование
ДЗ
11.04
Знакомство с анализом данных в среде R
18.04
Семинар по проблемам ПА (доклады по статьям) + защита персональных проектов
* тема для самостоятельного освоения с использованием тематической лекции Д.Н. Козлова в дисциплине «Введение в специальность»
5.
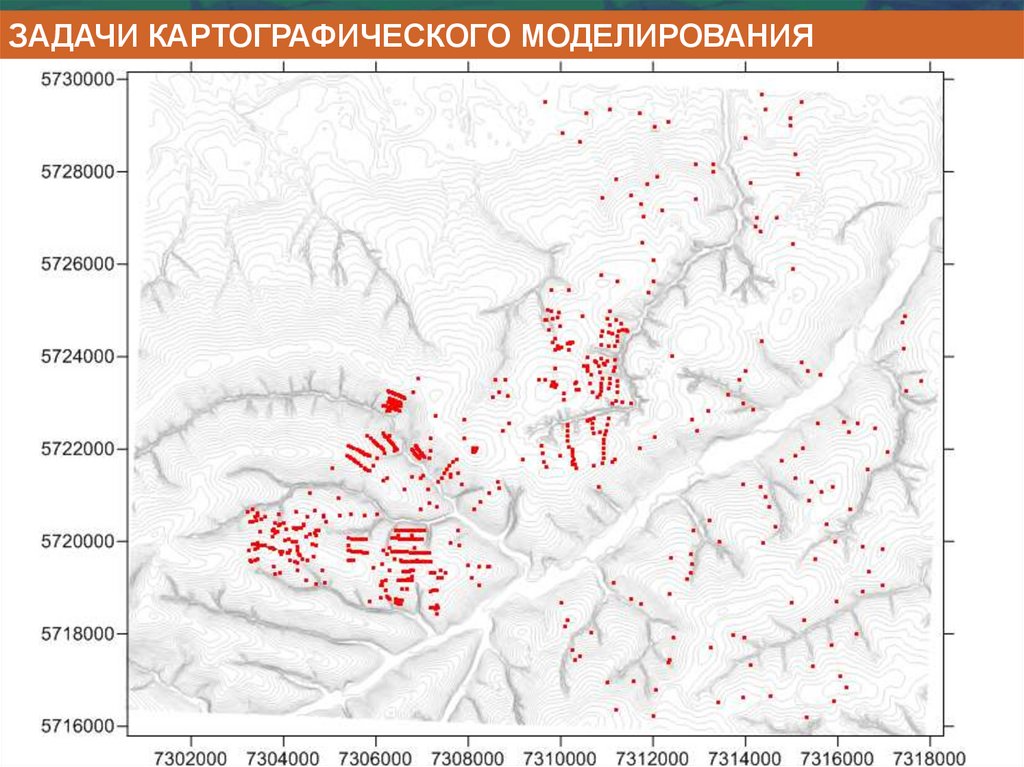
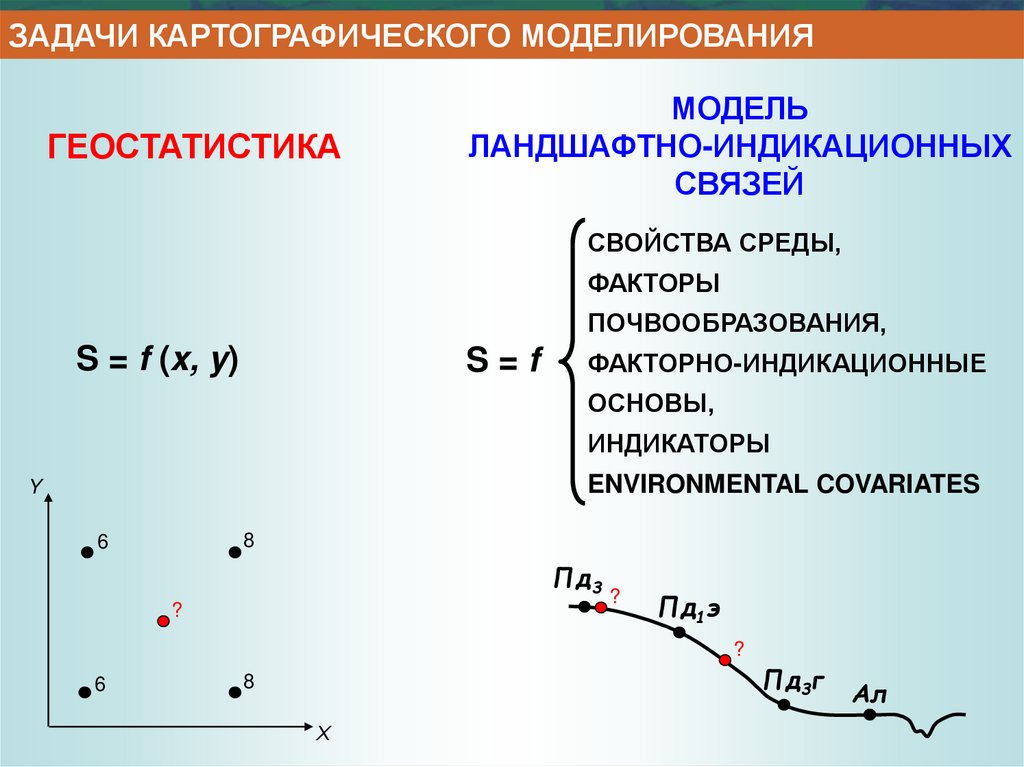
ЗАДАЧИ КАРТОГРАФИЧЕСКОГО МОДЕЛИРОВАНИЯ6.
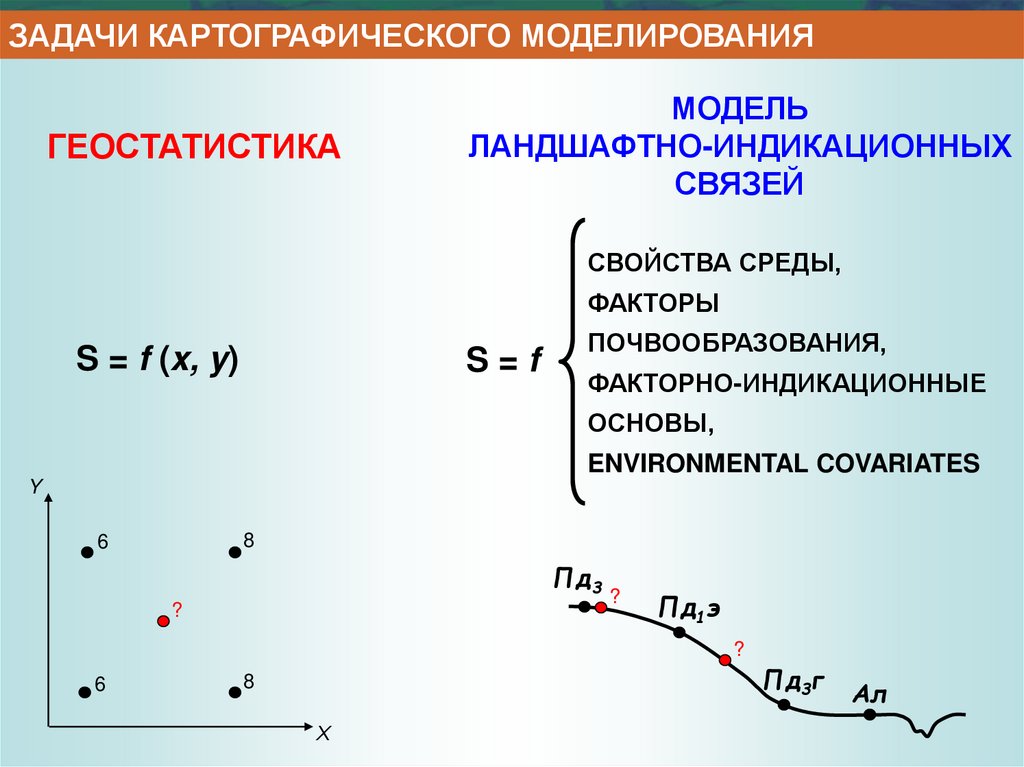
ЗАДАЧИ КАРТОГРАФИЧЕСКОГО МОДЕЛИРОВАНИЯГЕОСТАТИСТИКА
МОДЕЛЬ
ЛАНДШАФТНО-ИНДИКАЦИОННЫХ
СВЯЗЕЙ
СВОЙСТВА СРЕДЫ,
ФАКТОРЫ
ПОЧВООБРАЗОВАНИЯ,
S = f (x, y)
S=f
ФАКТОРНО-ИНДИКАЦИОННЫЕ
ОСНОВЫ,
ИНДИКАТОРЫ
ENVIRONMENTAL COVARIATES
Y
8
6
Пд3
?
?
Пд1э
?
6
Пд3г
8
Х
Ал
7.
ГЕОСТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕОливье Дюбрул
Использование
геостатистики для
включения в
геологическую модель
сейсмических данных,
EAGE, 2002
http://rutracker.org/forum/vie
wtopic.php?t=2583257
Демьянов В.В., Савельева
Е.А. Геостатистика теория
и практика / под ред. Р. В .
Арутюняна; Ин-т проблем
безопасного развития
атомной энергетики РАНМ.:
Москва, "Наука", 2010 г. - 327
стр.
http://gislab.info/docs/saveliev201
2-geostat.pdf
8.
ГЕОСТАТИСТИКА: ОБЛАСТЬ ПРИМЕНЕНИЯМОДЕЛИРОВАНИЕ ОБЪЕМА РЕЗЕРВУАРОВ (рудного тела,
месторождения нефти, газа и т.п.)
1951 - Дэни Криг (Danie Krige), золоторудный рудник в ЮАР
1968 - Жорж Матерон разработал геостатистический подход, как
теорию регионализиванных (пространственных)
переменных, для анализа данных о природных ископаемых
(горнорудное дело)
МОДЕЛИРОВАНИЕ ПОЛЕЙ (рельефа, метеохарактеристик и др.)
1963 - Л.С. Гандин, теория оптимальной интерполяции для
объективного анализа метеополей включала основы
геостатистической теории
СРАВНЕНИЕ ЯВЛЕНИЙ, измеренных в «разных» точках (+, -, *, /)
9.
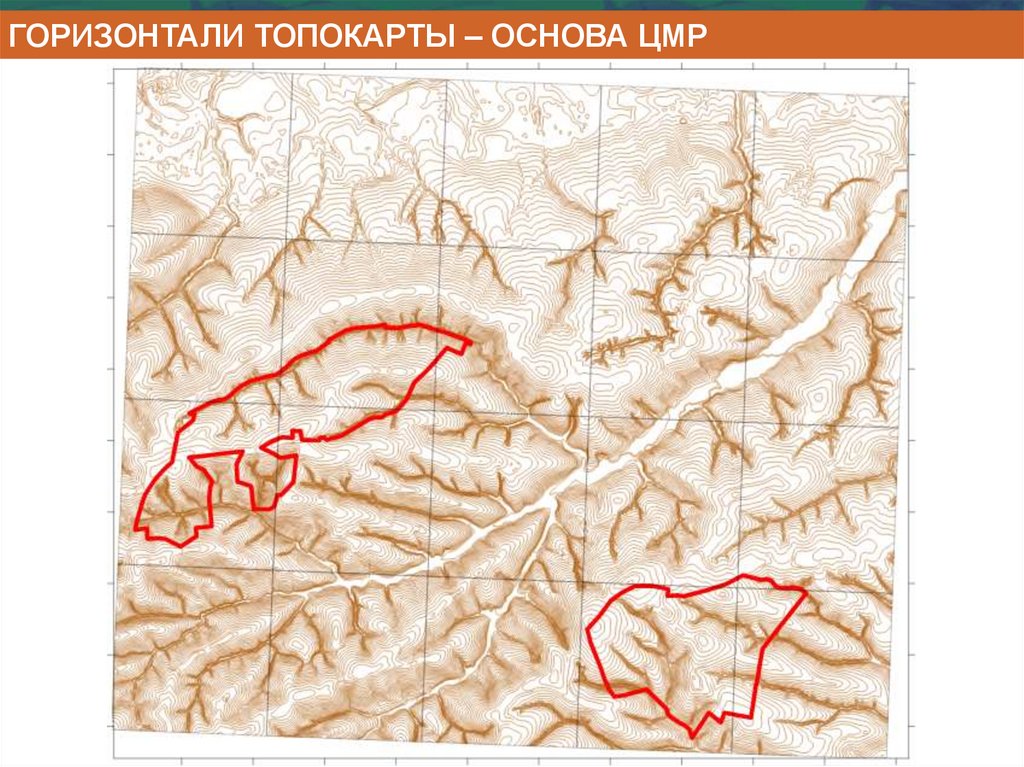
ЦИФРОВЫЕ МОДЕЛИ РЕЛЬЕФА (ЦМР)- визуализация (изолинии,
3D и др.)
- моделирование
процессов,
контролируемых
рельефом
(гидрологический сток,
распространения
загрязнителя и др.)
- составление карты
элементов, форм и типов
рельефа
-…
10.
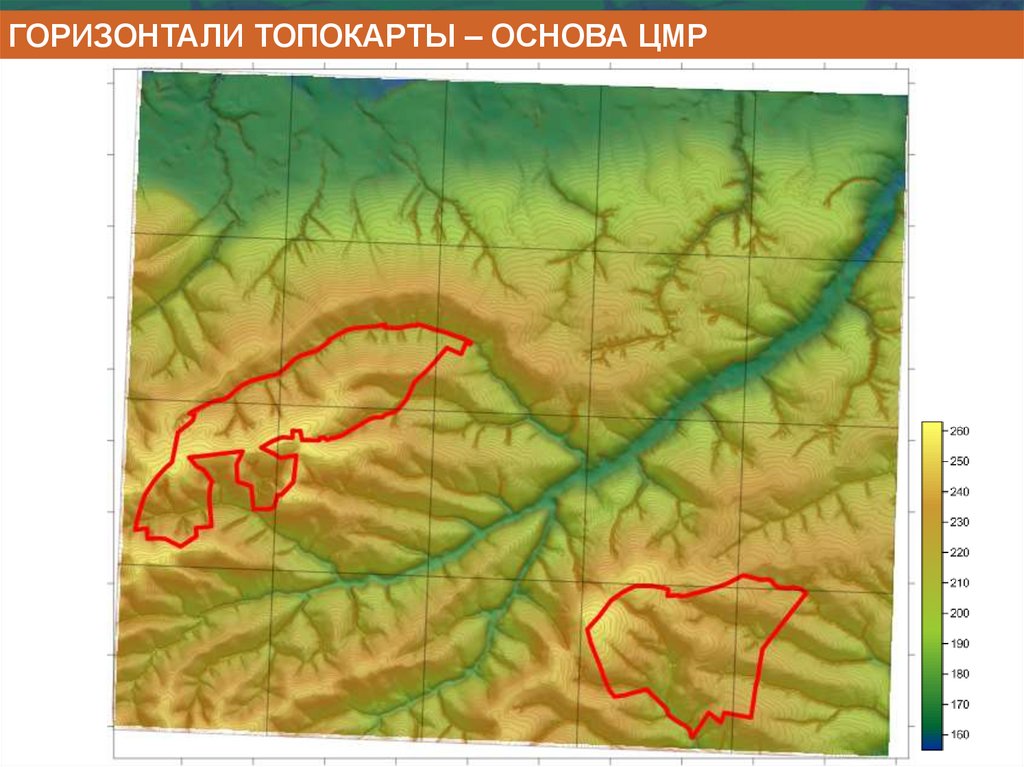
ГОРИЗОНТАЛИ ТОПОКАРТЫ – ОСНОВА ЦМР11.
ГОРИЗОНТАЛИ ТОПОКАРТЫ – ОСНОВА ЦМР12.
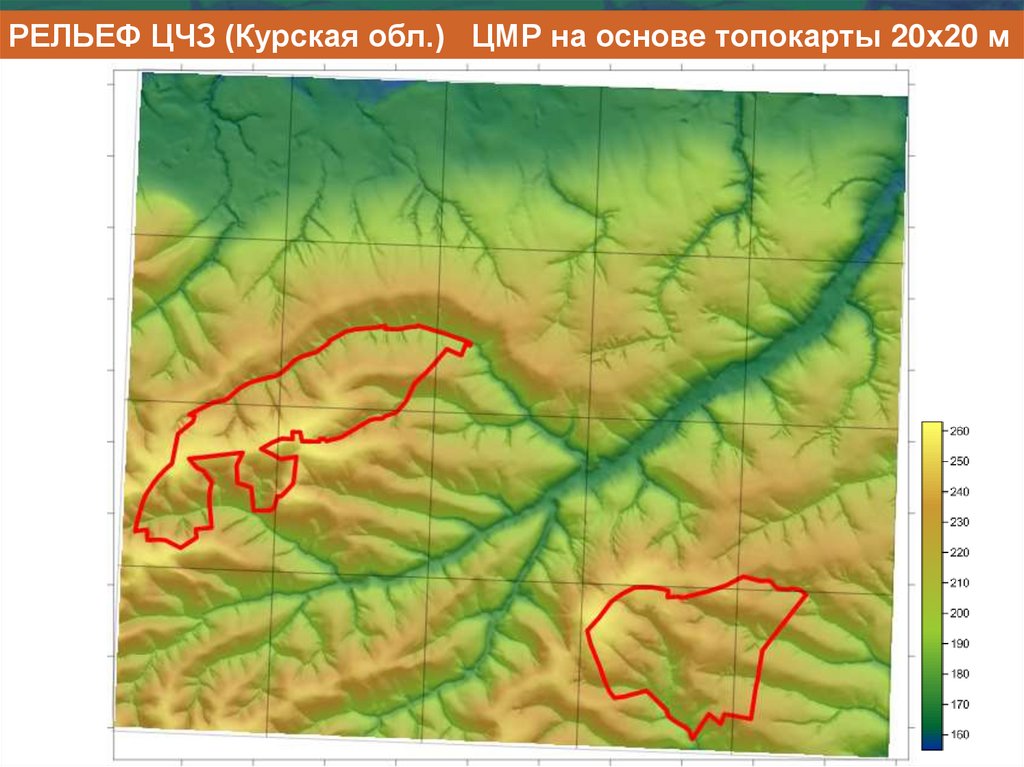
РЕЛЬЕФ ЦЧЗ (Курская обл.) ЦМР на основе топокарты 20х20 м13.
ЦЧЗ: цифровая основа карты элементов мезорельефаФ*
П
U
Э**
Градации крутизны склонов
0-1.2°
1.2-2.5°
2.5-5°
5-10°
>10°
С
Ю
С
Ю
Легенда: Ф* - форма склонов в плане (П – выпуклые, U –
вогнутые), Э** - ориентация склонов: С – северной экспозиции
(холодные), Ю – южной экспозиции (теплые)
14.
ГЕОФИЗИЧЕСКАЯ ДИФФЕРЕНЦИАЦИЯ ГЕОСИСТЕМЭлементарный ПТК - приурочен к одному элементу мезорельефа;
это территория однородная по трем своим характеристикам:
литологическому составу пород, углам наклона рельефа и
экспозиции склона
В этом случае суммарная солнечная радиация и атмосферные осадки,
поступающие на поверхность, одинаковы. Поэтому формируются один
микроклимат и один водный режим, один биогеоценоз, одна почвенная разность
и однообразный комплекс почвенной мезофауны [Функционирование …., 2004]
Следовательно:
потенциальная дифференциация ПТК может быть определена на
множестве элементов поверхности рельефа отображением
морфометрических параметров описания градиентов полей инсоляции и
гравитации
Уравнения теории поля и дифференциальной геометрии
являются как минимум достаточным условием для
геофизического описания потенциальной дифференциации
природных территориальных комплексов
В.В. Сысуев, 2005
15.
ДВЕ РАЗНОВИДНОСТИ ЦМРРешетка (grid) – структура
регулярных вертикальных и
горизонтальных линий (колонок и
строк).
Синонимы: матрица, таблица,
растр
TIN (Triangulated Irregular Network)
– линейная нерегулярная сеть,
система не перекрывающихся
треугольников. Вершинами
треугольников являются исходные
опорные точки.
16.
ПОЛОЖЕНИЕ ТОЧЕК В ПРОСТРАНСТВЕРЕГУЛЯРНО И РАВНОМЕРНО
СЛУЧАЙНО И РАВНОМЕРНО
Y
Z1
Z3
Z2
Z4
Х
НЕ СЛУЧАЙНО и НЕ РАВНОМЕРНО
X
Y
Z
X1
Y1
Z1
X2
Y2
Z2
…
…
…
Xn
Yn
Zn
17.
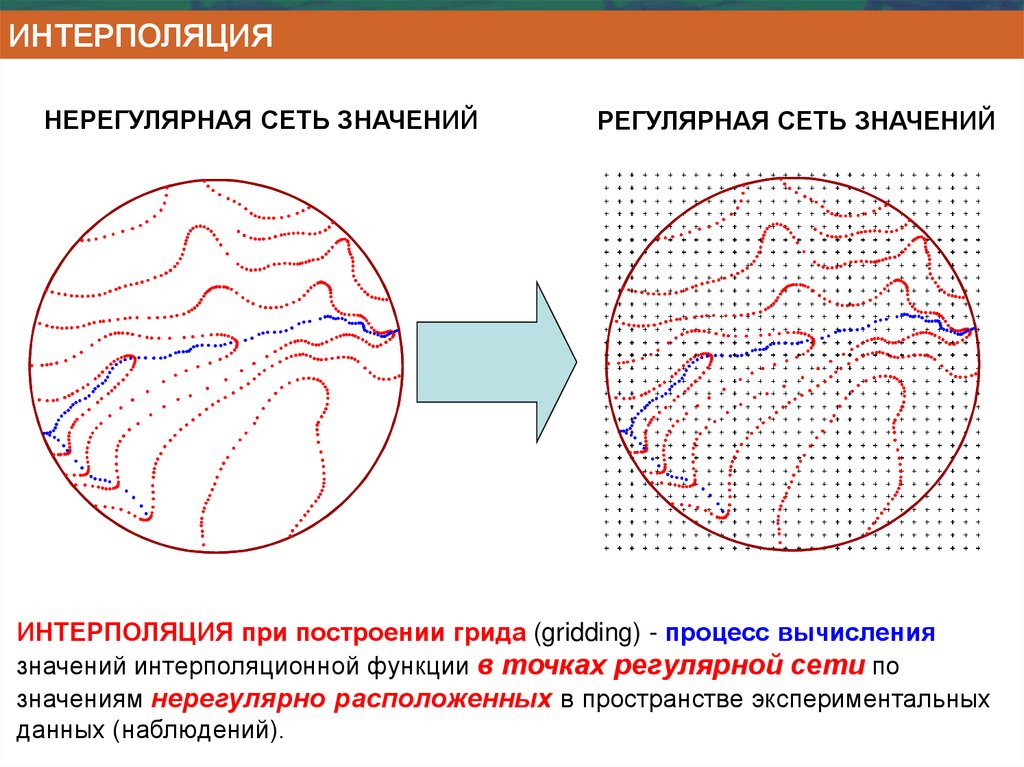
ИНТЕРПОЛЯЦИЯНЕРЕГУЛЯРНАЯ СЕТЬ ЗНАЧЕНИЙ
РЕГУЛЯРНАЯ СЕТЬ ЗНАЧЕНИЙ
ИНТЕРПОЛЯЦИЯ при построении грида (gridding) - процесс вычисления
значений интерполяционной функции в точках регулярной сети по
значениям нерегулярно расположенных в пространстве экспериментальных
данных (наблюдений).
18.
ИНТЕРПОЛЯЦИЯY
Y
Y
8
6
6.7
8.4
6.1
6.5
5.9
?
?
9.2
7.4
6.8
?
7.2
6.4
5.7
8
6.5
Х
9.1
5.1
5.6
Х
8.9
7.8
6.1
6
8.8
8.0
5.8
8.6
6.9
6.8
Х
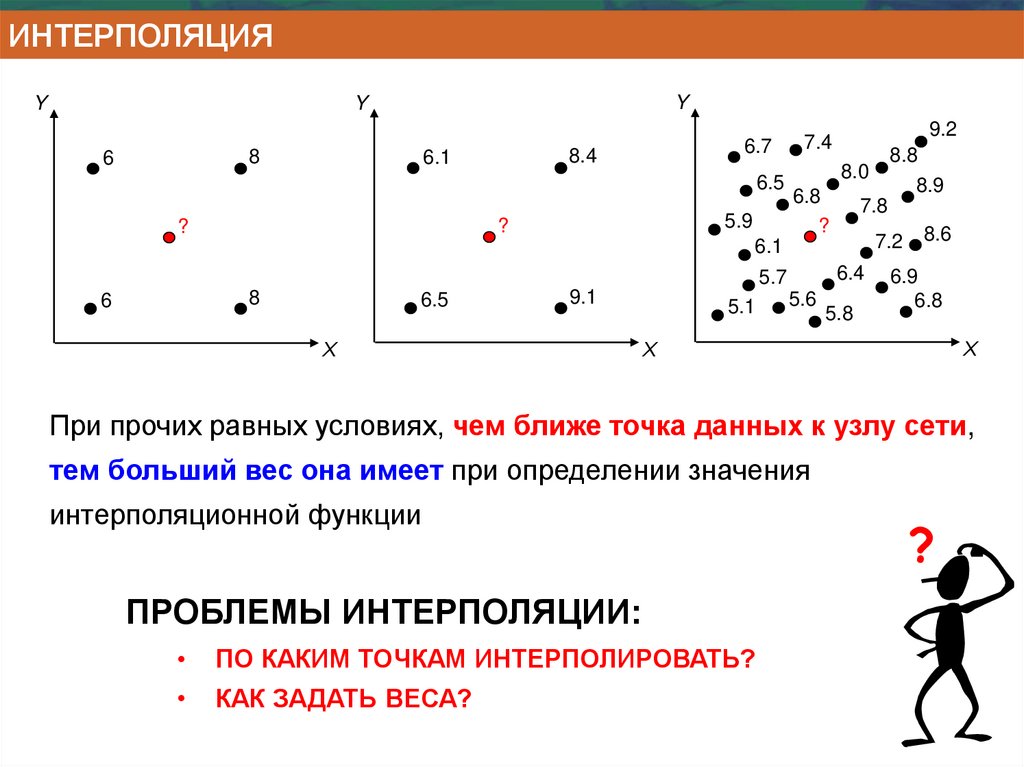
При прочих равных условиях, чем ближе точка данных к узлу сети,
тем больший вес она имеет при определении значения
интерполяционной функции
ПРОБЛЕМЫ ИНТЕРПОЛЯЦИИ:
ПО КАКИМ ТОЧКАМ ИНТЕРПОЛИРОВАТЬ?
КАК ЗАДАТЬ ВЕСА?
19.
ИНТЕРПОЛЯЦИЯ на основе обратного расстояния (IDV)1.
2.
Определить n ближайших
точек к заданной точке k.
Вычислить расстояние Dik от
точки с номером i до точки с
номером k по теореме
Пифагора
D ik
3.
X1k X1i 2 X 2k X 2i 2
Вычислить значение Yk по
формуле
?
n
Высота
(Y), m
Дистанция
(D), m
248.8
283.5
248.5
406.5
248.3
485.2
255.8
558.7
247.3
450.3
245.9
454.6
240.8
[-] – как задать «ближайшие» точки?
(по числу, по расстоянию, по направлению?)
534.3
Yk
Y /D
i 1
n
ik
1/D
i 1
Yk
i
ik
3.9993
247.9
0.0161
20.
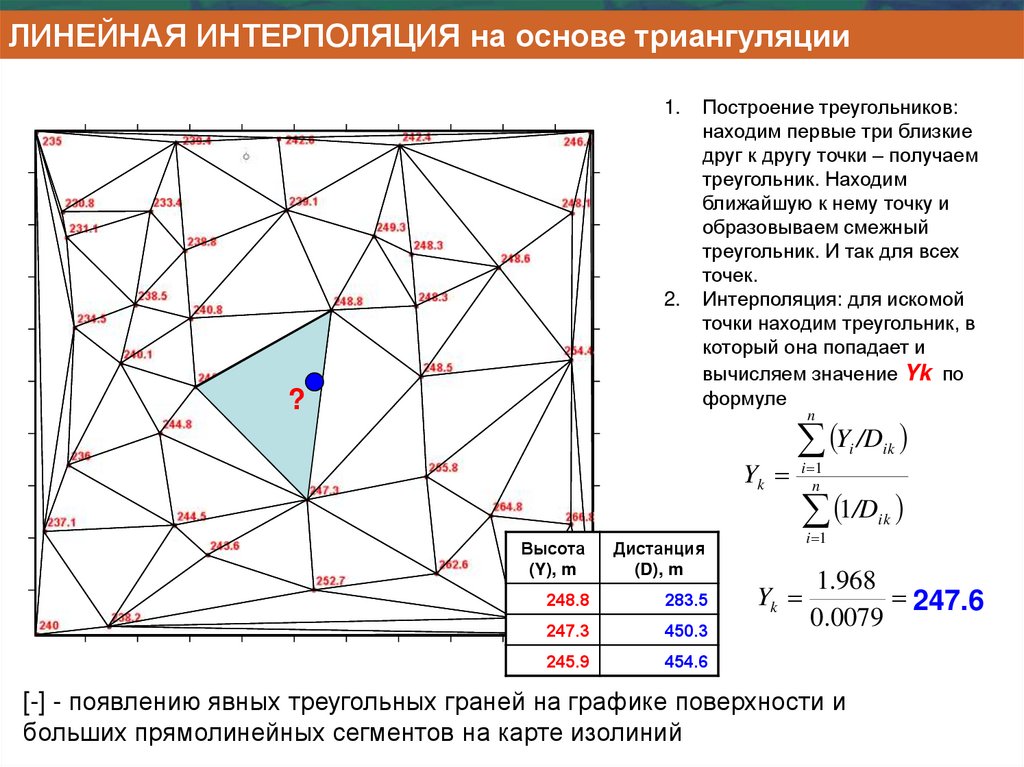
ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ на основе триангуляции1.
2.
?
Построение треугольников:
находим первые три близкие
друг к другу точки – получаем
треугольник. Находим
ближайшую к нему точку и
образовываем смежный
треугольник. И так для всех
точек.
Интерполяция: для искомой
точки находим треугольник, в
который она попадает и
вычисляем значение Yk по
формуле
n
Y /D
Yk i n1
i
ik
1/D
Высота
(Y), m
Дистанция
(D), m
248.8
283.5
247.3
450.3
245.9
454.6
i 1
Yk
ik
1.968
247.6
0.0079
[-] - появлению явных треугольных граней на графике поверхности и
больших прямолинейных сегментов на карте изолиний
21.
МЕТОДЫ ИНТЕРПОЛЯЦИИМетод обратных расстояний (Inverse Distance to a Power) является достаточно быстрым, но
имеет тенденцию генерировать структуры типа "бычий глаз" вокруг точек наблюдений с высокими
значениями функции.
Метод Криге (Kriging) - один из наиболее гибких и часто используемых методов. Этот метод
задается в SURFERе по умолчанию. Для большинства множеств экспериментальных данных метод
Криге с линейной вариаграммой является наиболее эффективным. Однако, на множествах большого
размера он работает медленно.
Метод минимума кривизны (Minimum Curvature)
генерирует гладкие поверхности и для
большинства множеств экспериментальных данных работает достаточно быстро.
Метод полиномиальной регрессии (Polynomial Regression) используется для выделения больших
трендов и структур в Ваших данных. Это метод работает очень быстро для множеств любого
размера, но, строго говоря, он не является интерполяционным методом, поскольку сгенерированная
поверхность не проходит через экспериментальные точки.
Метод радиальных базисных функций (Radial Basis Functions) так же, как и метод Криге, является
очень гибким и генерирует гладкую поверхность,
проходящую через экспериментальные точки.
Результаты работы этого метода очень похожи на результаты метода Криге. Он эффективен для
большинства множеств экспериментальных данных.
Метод Шепарда (Shepard's Method) подобен методу обратных расстояний (Inverse Distance to a
Power), но он, как правило, не генерирует структуры типа "бычий глаз", особенно когда задан
сглаживающий параметр.
Метод триангуляции (Triangulation with Linear Interpolation) для множеств экспериментальных
точек средних размеров (от 250 до 1000 наблюдений) работает достаточно быстро и строит хорошее
представление данных. Этот метод генерирует явные треугольные грани на графике поверхности.
Руководство пользователя к программе Surfer 6.0
22.
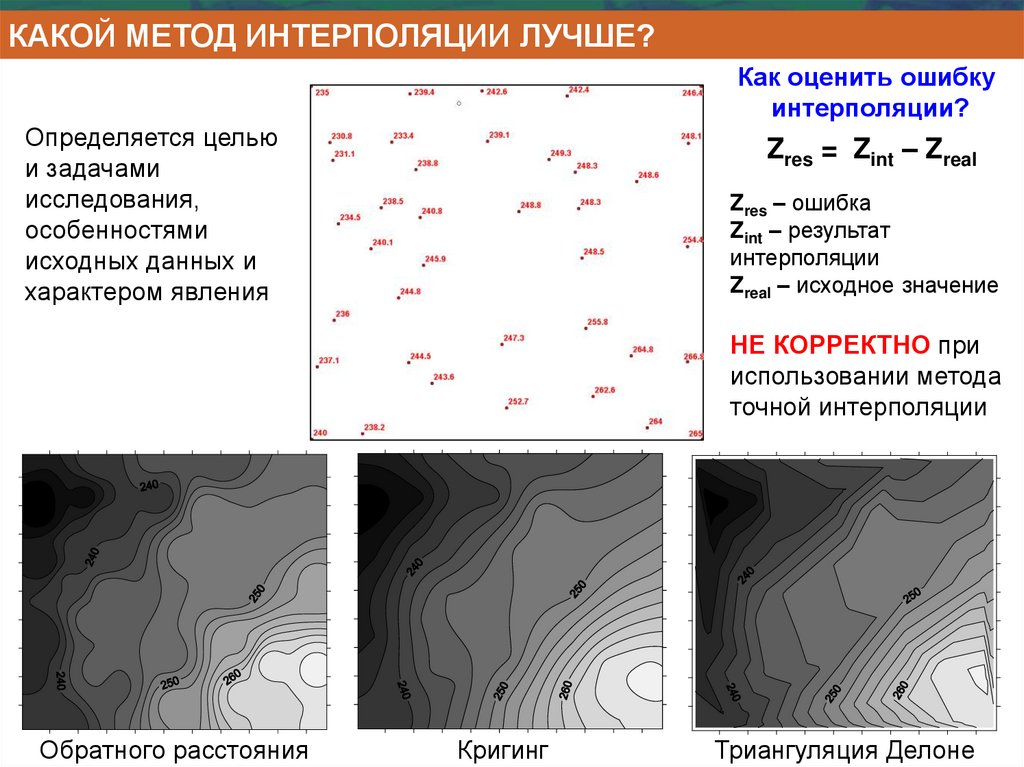
КАКОЙ МЕТОД ИНТЕРПОЛЯЦИИ ЛУЧШЕ?Как оценить ошибку
интерполяции?
Определяется целью
и задачами
исследования,
особенностями
исходных данных и
характером явления
Zres = Zint – Zreal
Zres – ошибка
Zint – результат
интерполяции
Zreal – исходное значение
НЕ КОРРЕКТНО при
использовании метода
точной интерполяции
Обратного расстояния
Кригинг
Триангуляция Делоне
23.
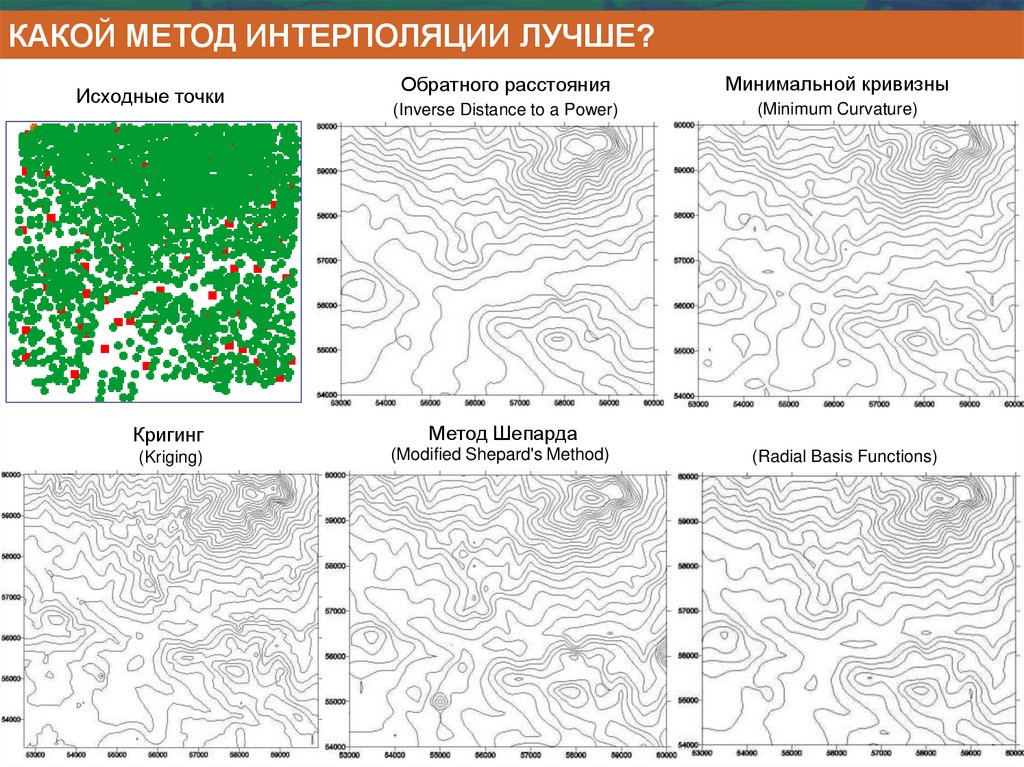
КАКОЙ МЕТОД ИНТЕРПОЛЯЦИИ ЛУЧШЕ?Исходные точки
Обратного расстояния
Минимальной кривизны
(Inverse Distance to a Power)
(Minimum Curvature)
Кригинг
Метод Шепарда
(Kriging)
(Modified Shepard's Method)
(Radial Basis Functions)
24.
КАКОЙ МЕТОД ИНТЕРПОЛЯЦИИ ЛУЧШЕ?Обратного расстояния
Сплайн интерполяция
Кригинг
(Inverse Distance to a Power)
(Spline)
(Kriging)
25.
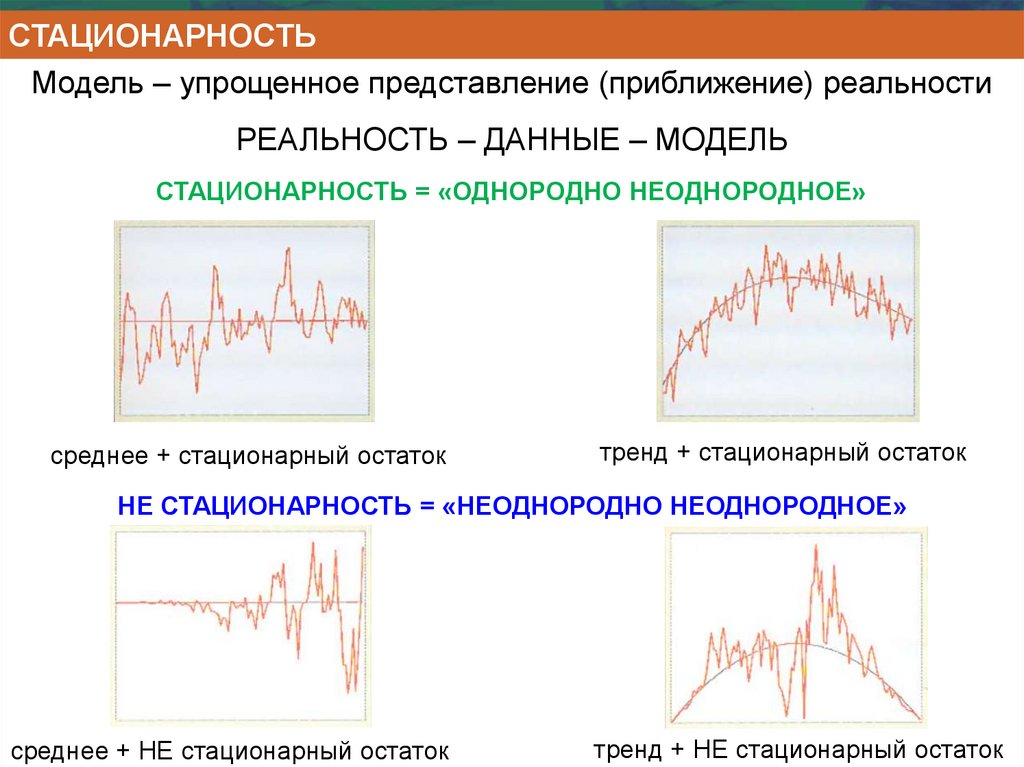
ГЕОСТАТИСТИЧЕСКАЯ МОДЕЛЬ ДАННЫХЕсли, среднее (Σ) и дисперсия (var) не зависят от местоположения
Σ[Z(x)] = Σ [Z(x+h)] = m
var([Z(x)] = var[Z(x+h)] = σ2
то ковариация значений в двух точках зависит только от расстояния между ними
Cov[Z(x), Z(x+h))] = C(h)
НО! При вычислении ковариации участвует среднее, вычисление которого требует
дополнительных ресурсов
C(h) и γ(h)
Стационарность относительно приращений:
С0
Σ[Z(x+h)-Z(x)]=0
½среднее[(Z(x+h)-Z(x))2] = γ(h) - вариограмма
γ(h) = C(0) - C(h)
γ(h) = C(0) - C(h)
h
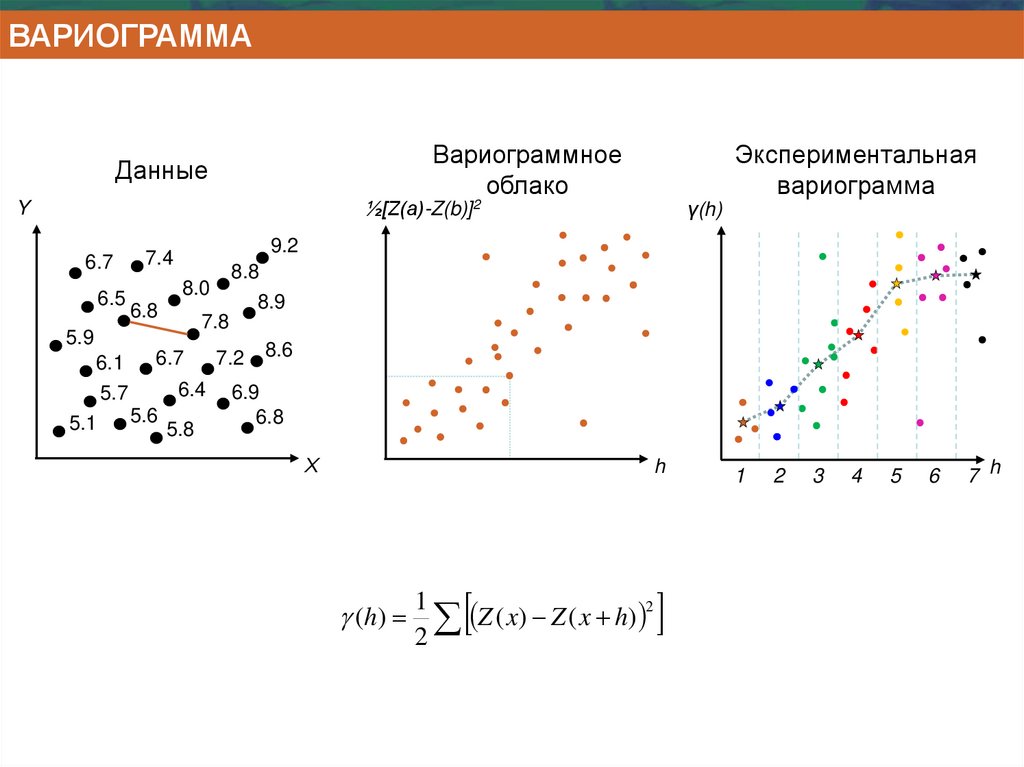
26.
ВАРИОГРАММАВариограммное
облако
Данные
½[Z(a)-Z(b)]2
Y
6.7
6.5
9.2
7.4
6.8
6.4
5.6
8.9
7.8
6.7
5.7
5.1
8.8
8.0
5.9
6.1
γ(h)
Экспериментальная
вариограмма
5.8
7.2
8.6
6.9
6.8
Х
h
( h)
1
Z ( x) Z ( x h) 2
2
1
2
3
4
5
6
7 h
27.
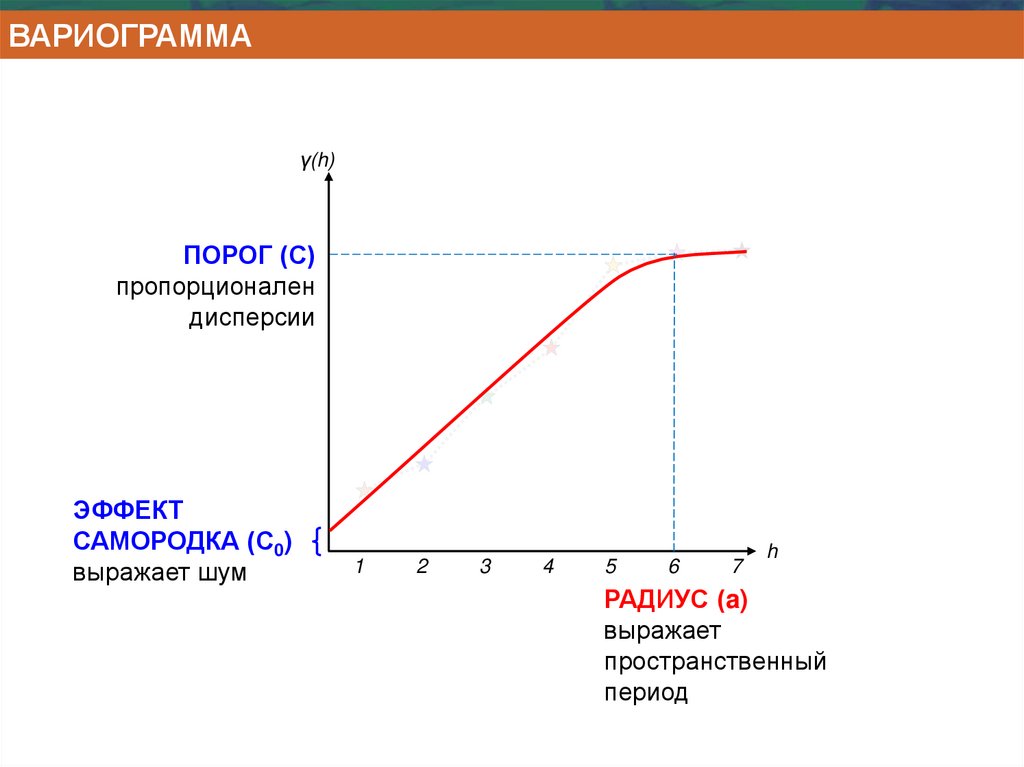
ВАРИОГРАММАγ(h)
ПОРОГ (С)
пропорционален
дисперсии
ЭФФЕКТ
САМОРОДКА (С0)
выражает шум
1
2
3
4
5
6
7
h
РАДИУС (a)
выражает
пространственный
период
28.
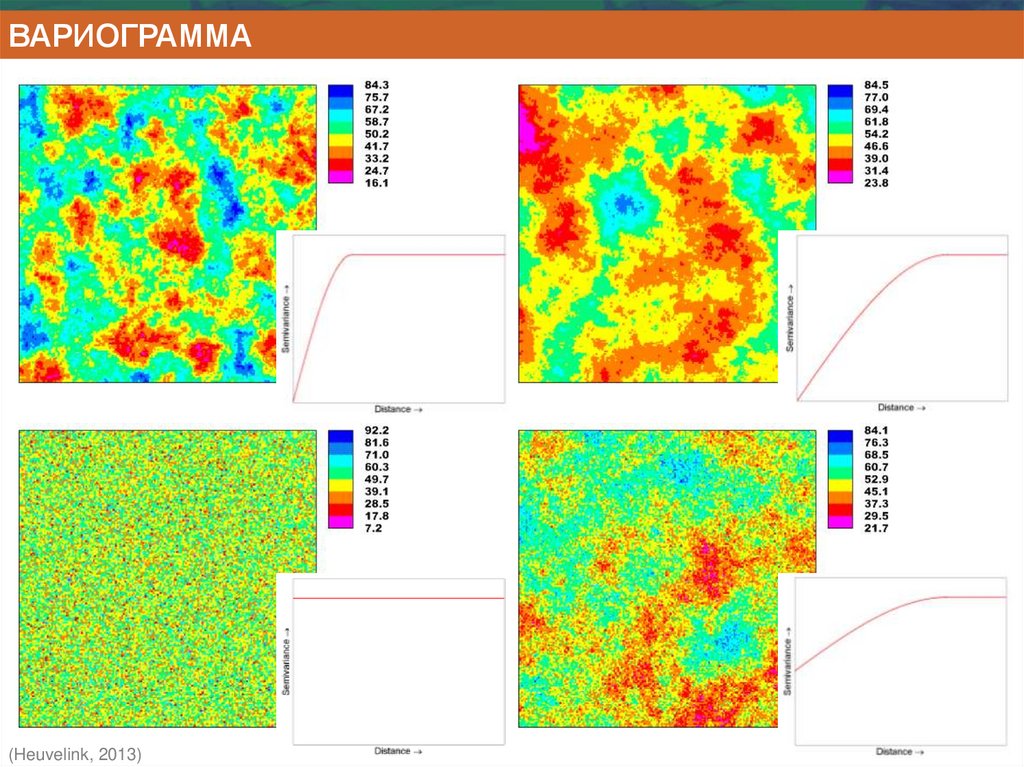
ВАРИОГРАММА(Heuvelink, 2013)
29.
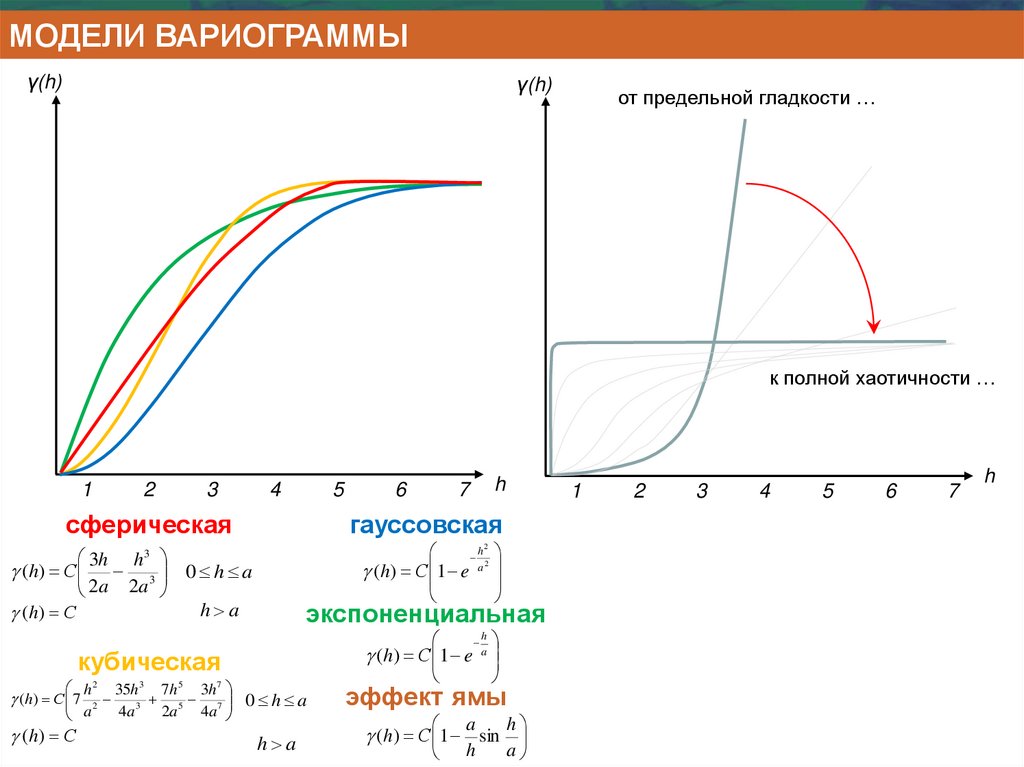
МОДЕЛИ ВАРИОГРАММЫγ(h)
γ(h)
от предельной гладкости …
к полной хаотичности …
1
2
3
4
5
сферическая
h
7
1
гауссовская
h
2
a
( h) С 1 e
2
3h h3
(h) С 3 0 h a
2a 2a
h a
( h) С
экспоненциальная
кубическая
h 2 35h3 7h5 3h 7
0 h a
2
4a 3 2a 5 4a 7
a
(h) С 7
( h) С
6
h a
h
a
(h) С 1 e
эффект ямы
a
h
(h) С 1 sin
h
a
2
3
4
5
6
7
h
30.
МОДЕЛИ ВАРИОГРАММЫγ(h)
1
2
3
4
5
сферическая
h
7
гауссова
h
2
a
( h) С 1 e
2
3h h3
(h) С 3 0 h a
2a 2a
h a
( h) С
экспоненциальная
кубическая
h 2 35h3 7h5 3h 7
0 h a
2
4a 3 2a 5 4a 7
a
(h) С 7
( h) С
6
h a
h
a
(h) С 1 e
эффект ямы
a
h
(h) С 1 sin
h
a
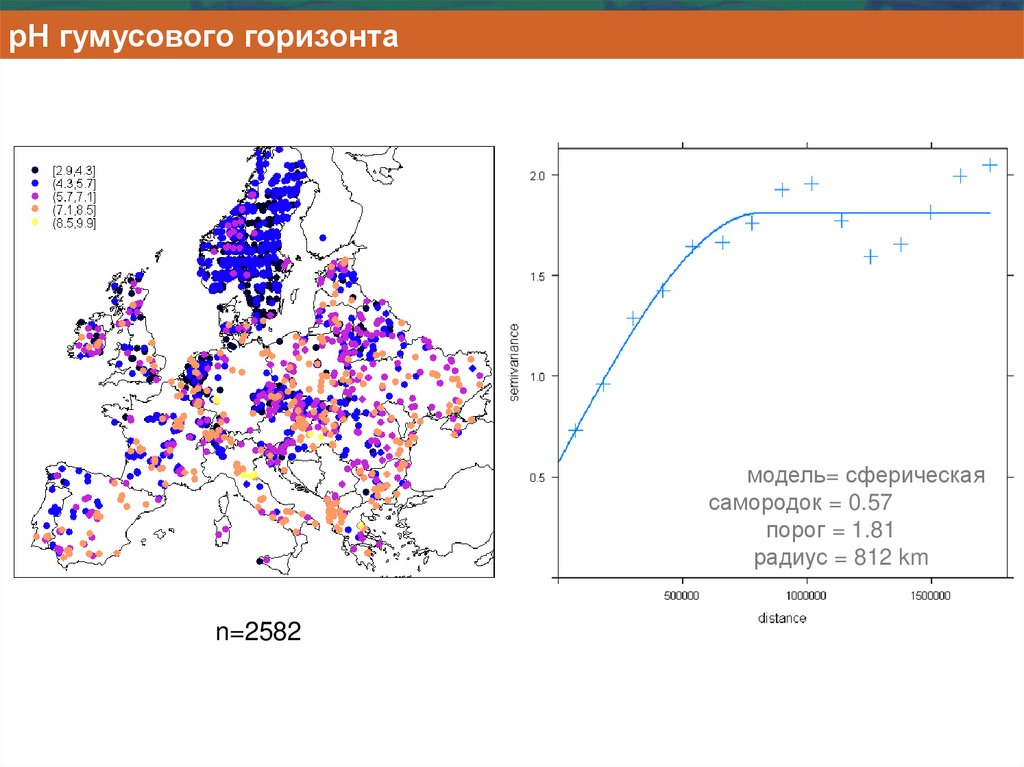
31.
рН гумусового горизонтамодель= сферическая
самородок = 0.57
порог = 1.81
радиус = 812 km
n=2582
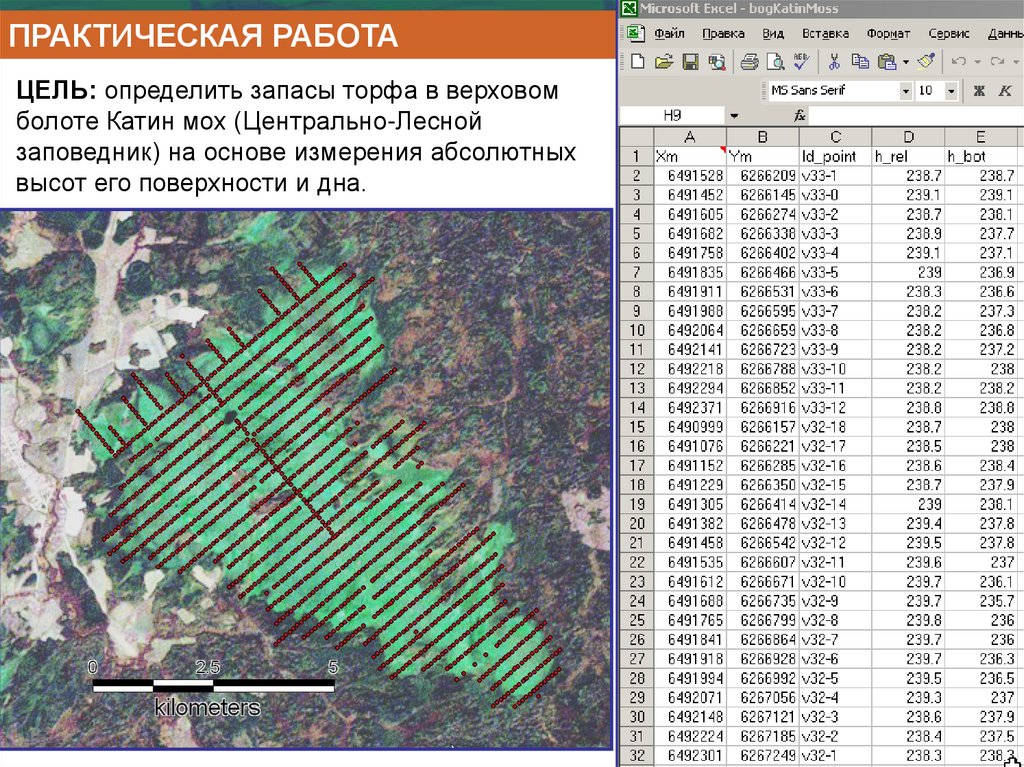
32.
рН гумусового горизонтаn=2582
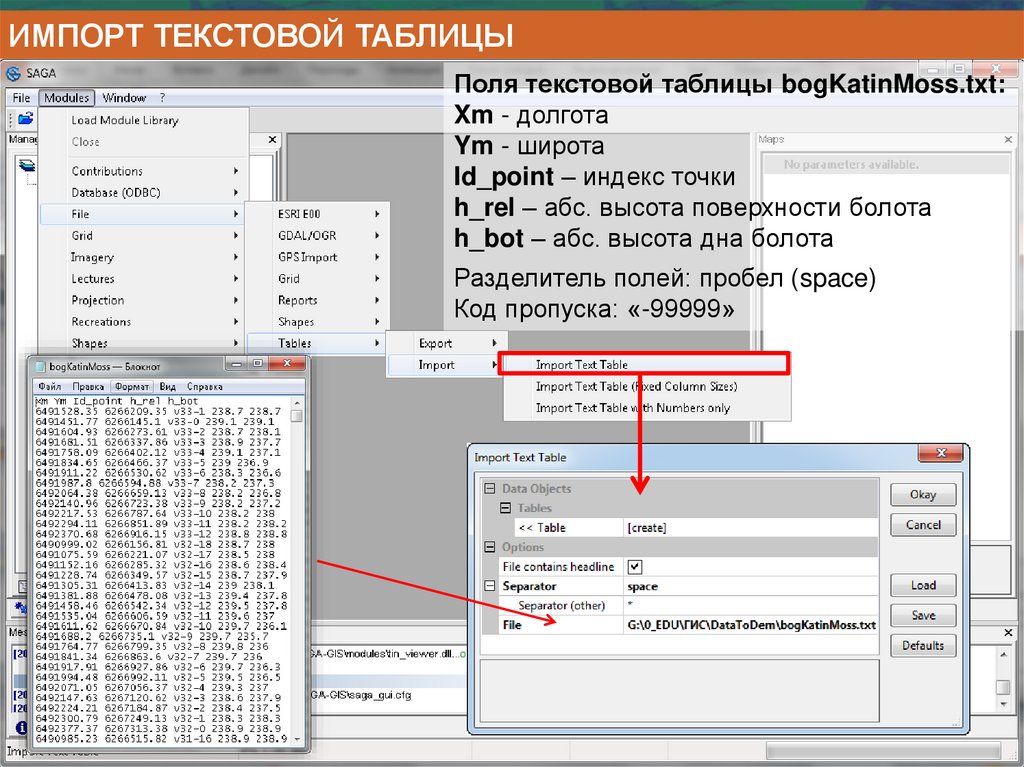
33.
рН гумусового горизонтаn=2582
34.
ЗАДАЧИ КАРТОГРАФИЧЕСКОГО МОДЕЛИРОВАНИЯГЕОСТАТИСТИКА
МОДЕЛЬ
ЛАНДШАФТНО-ИНДИКАЦИОННЫХ
СВЯЗЕЙ
СВОЙСТВА СРЕДЫ,
ФАКТОРЫ
S = f (x, y)
S=f
ПОЧВООБРАЗОВАНИЯ,
ФАКТОРНО-ИНДИКАЦИОННЫЕ
ОСНОВЫ,
ENVIRONMENTAL COVARIATES
Y
8
6
Пд3
?
?
Пд1э
?
6
Пд3г
8
Х
Ал
35.
РЕГРЕССИОННЫЙ КРИГИНГГЕОСТАТИСТИКА
МОДЕЛЬ
ЛАНДШАФТНО-ИНДИКАЦИОННЫХ
СВЯЗЕЙ
СВОЙСТВА СРЕДЫ,
ФАКТОРЫ
S = f (x, y)
S=f
ПОЧВООБРАЗОВАНИЯ,
ФАКТОРНО-ИНДИКАЦИОННЫЕ
ОСНОВЫ,
ENVIRONMENTAL COVARIATES



























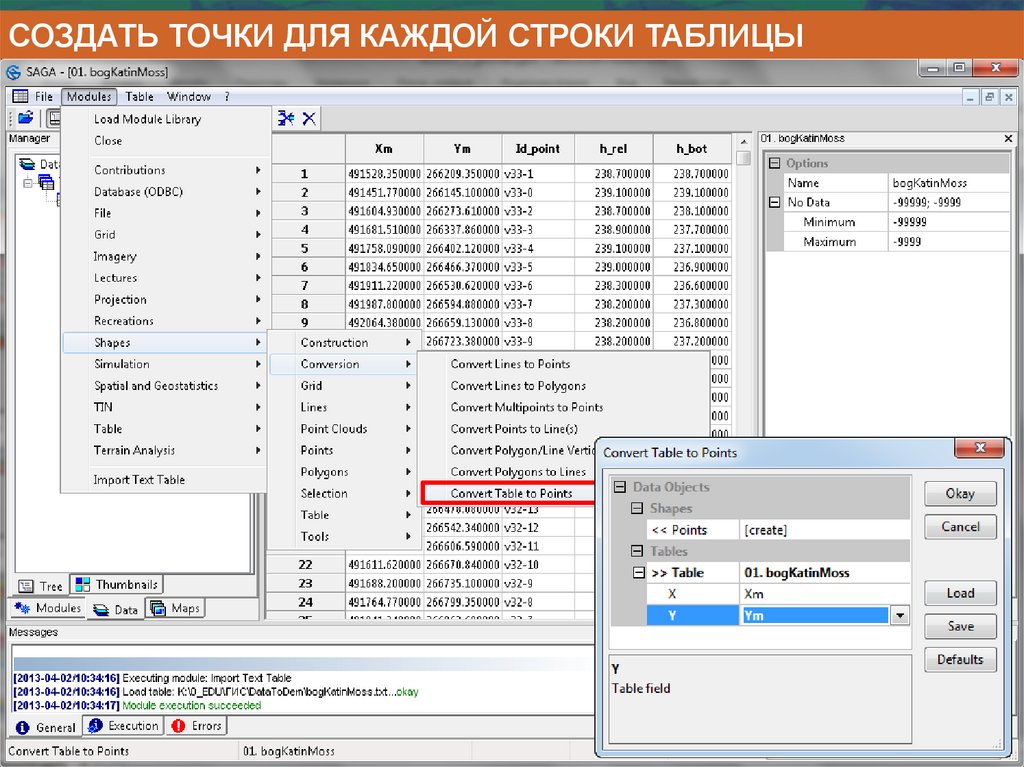

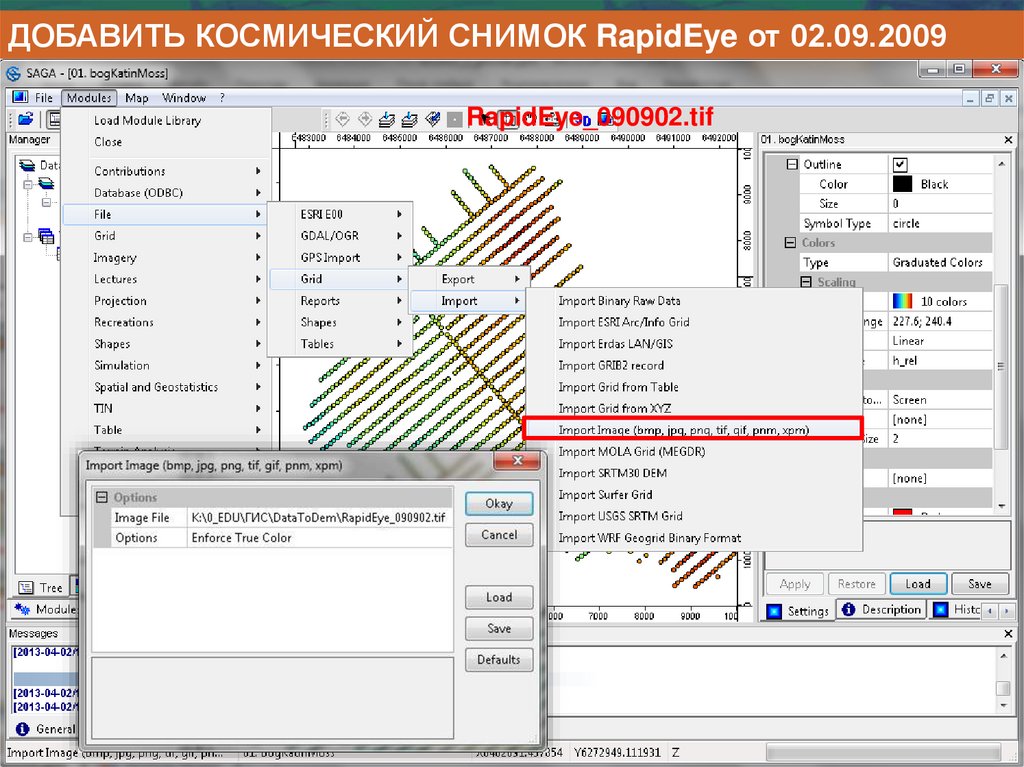
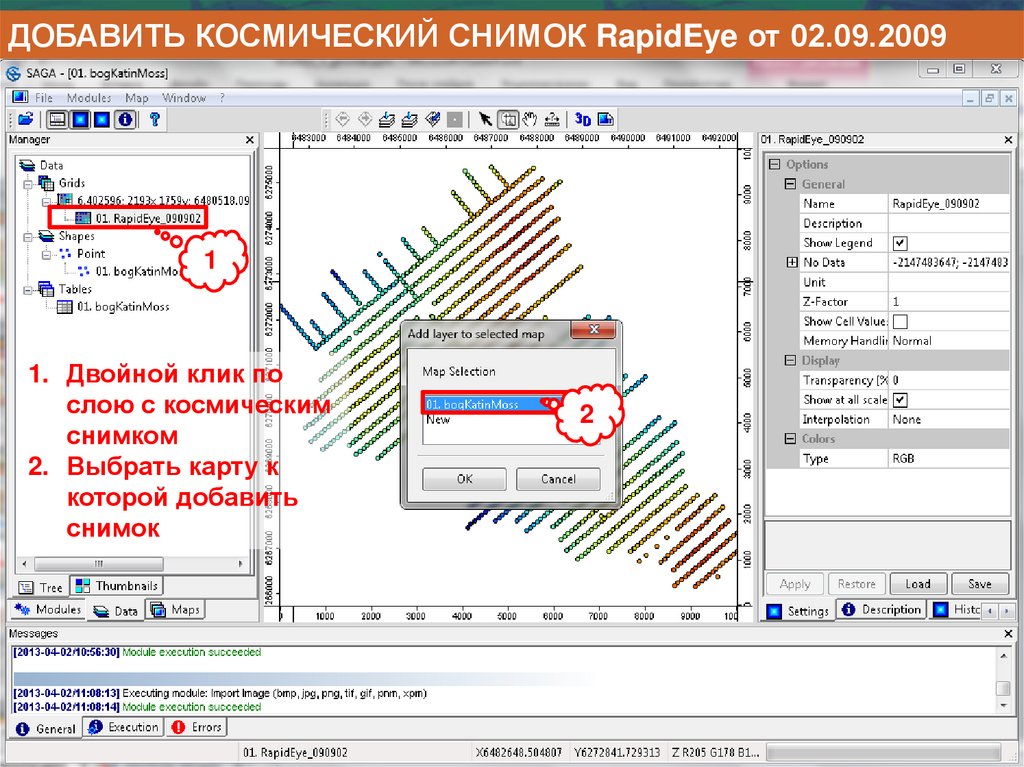
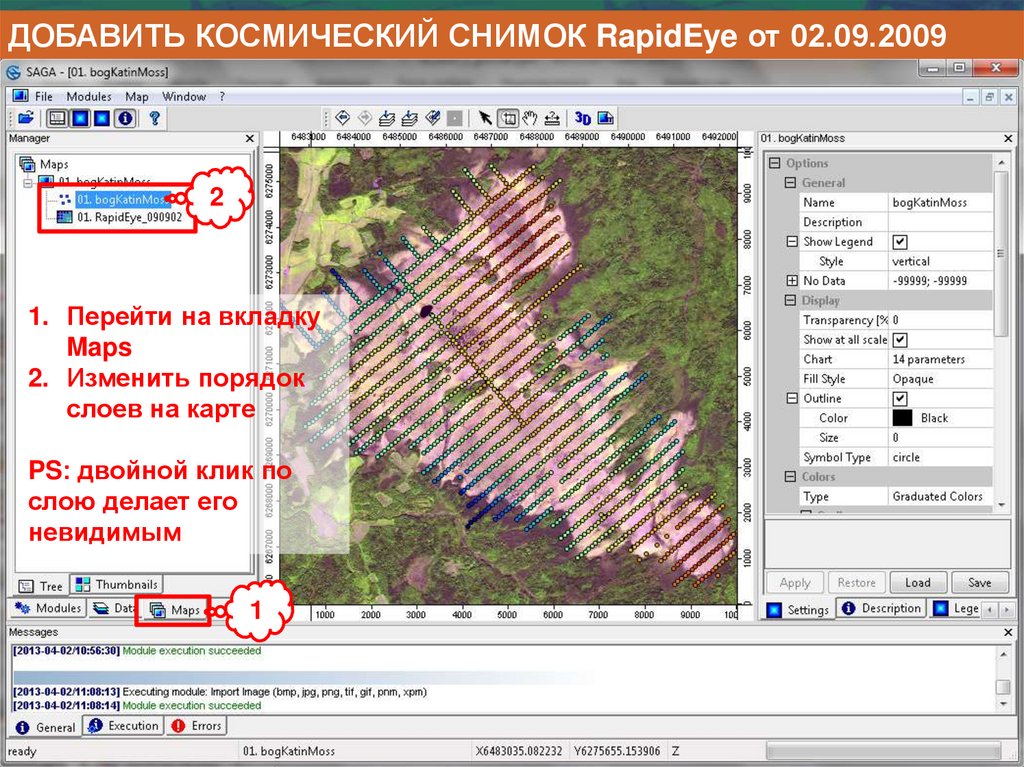
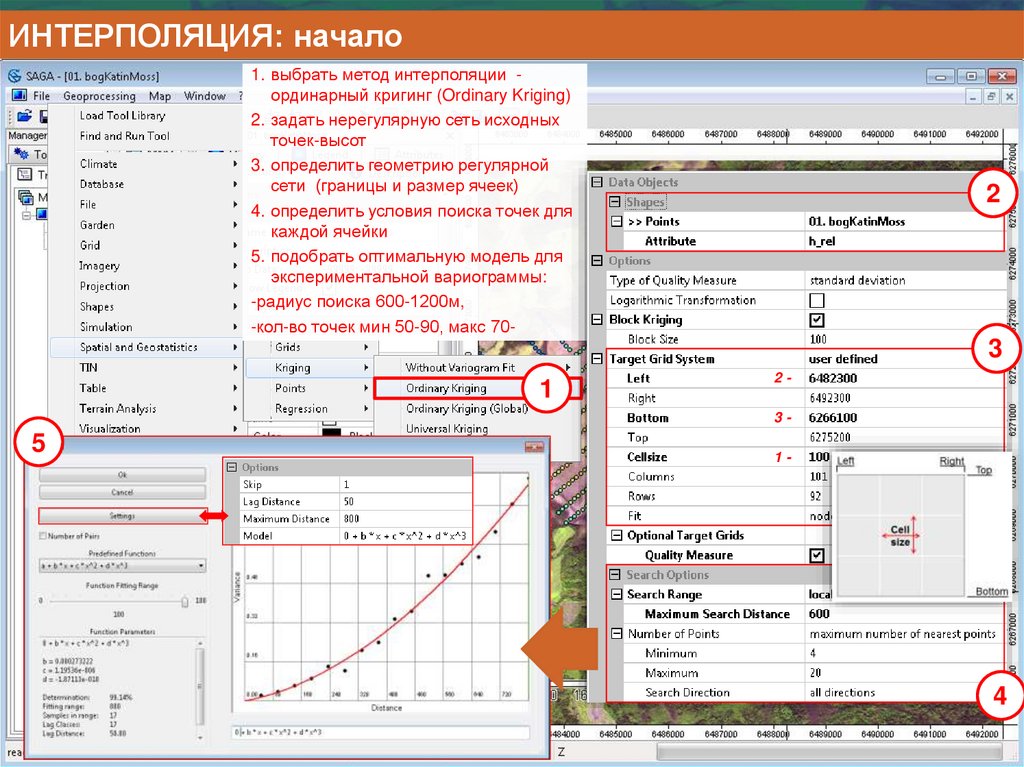

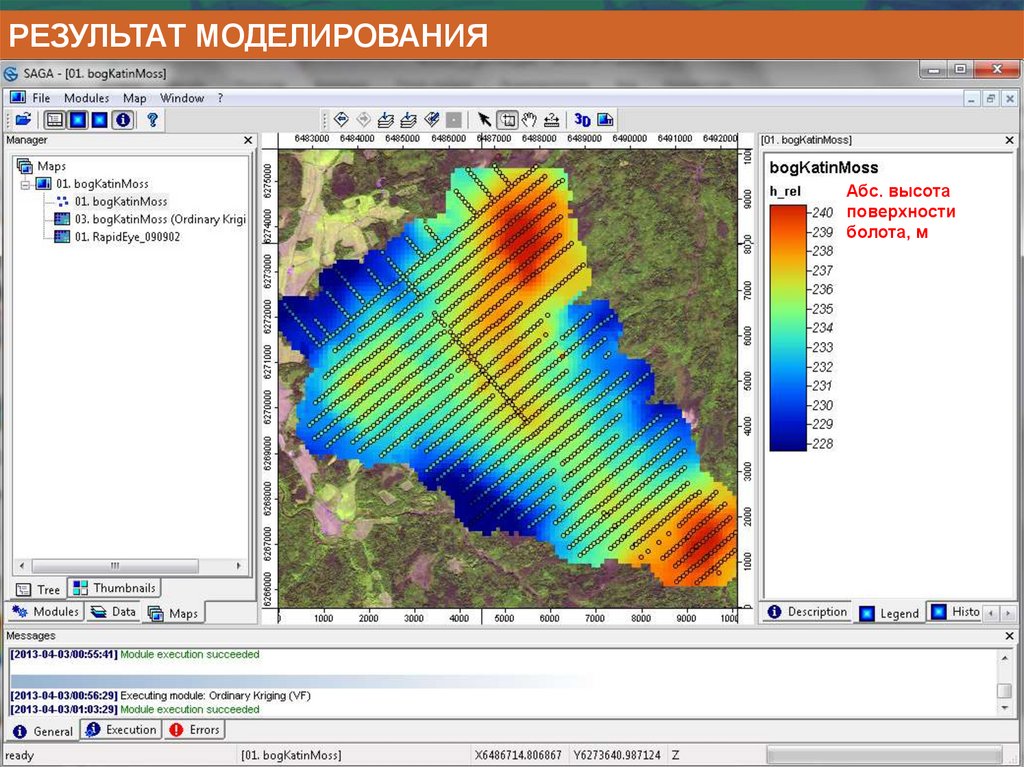
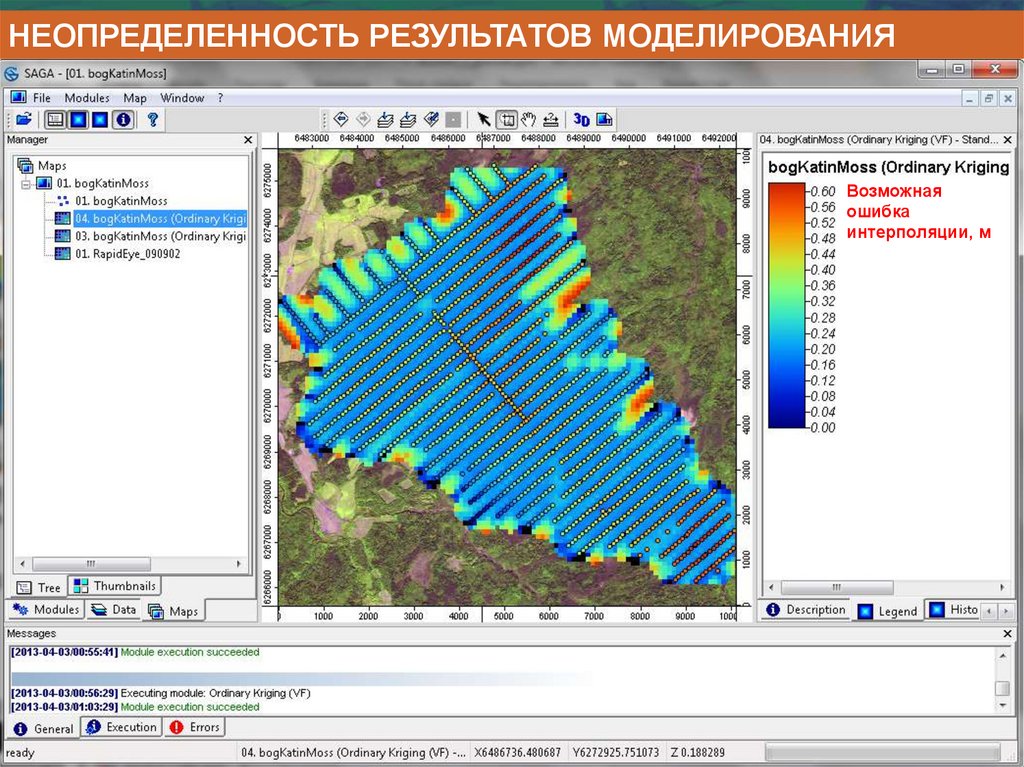
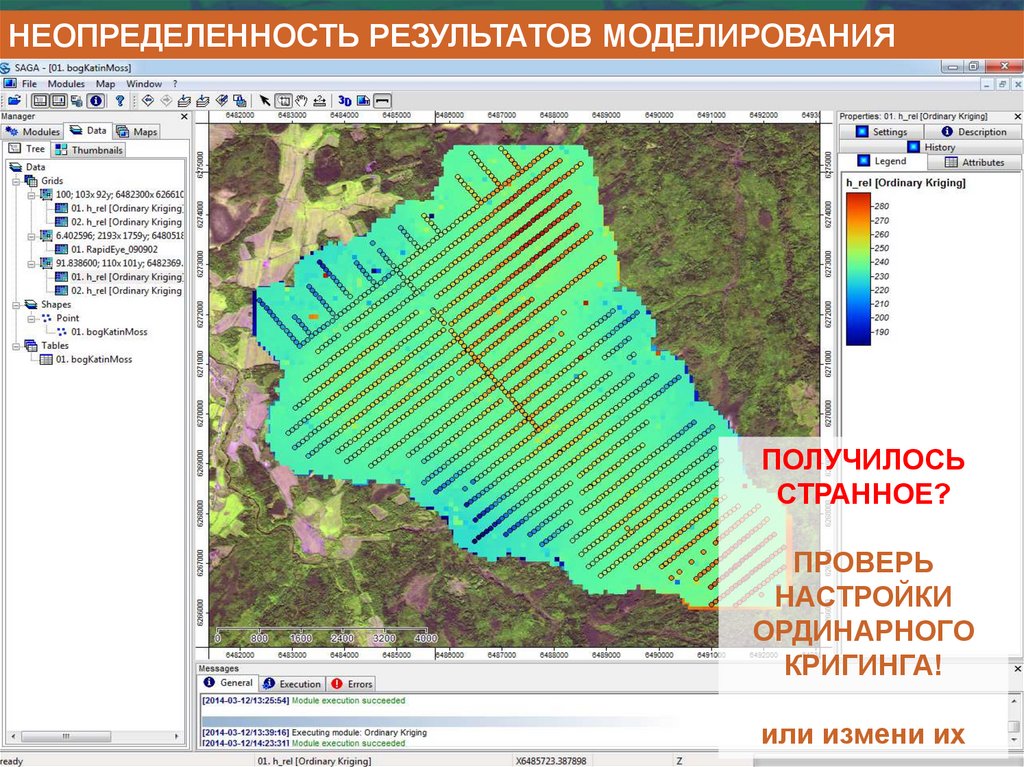
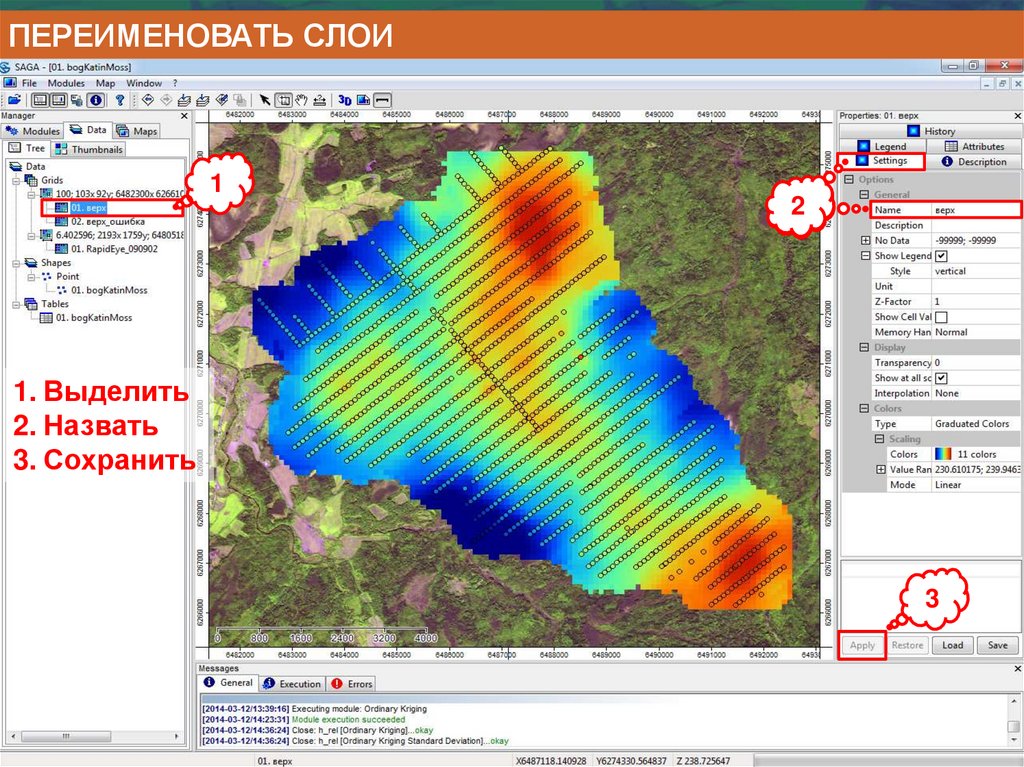

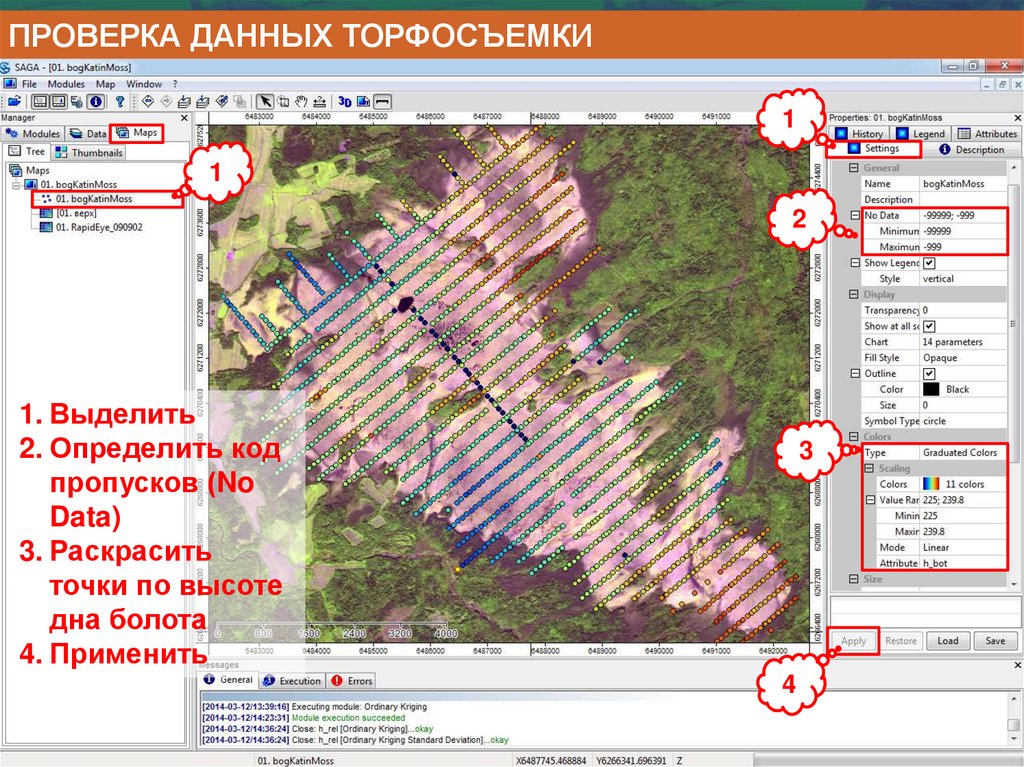
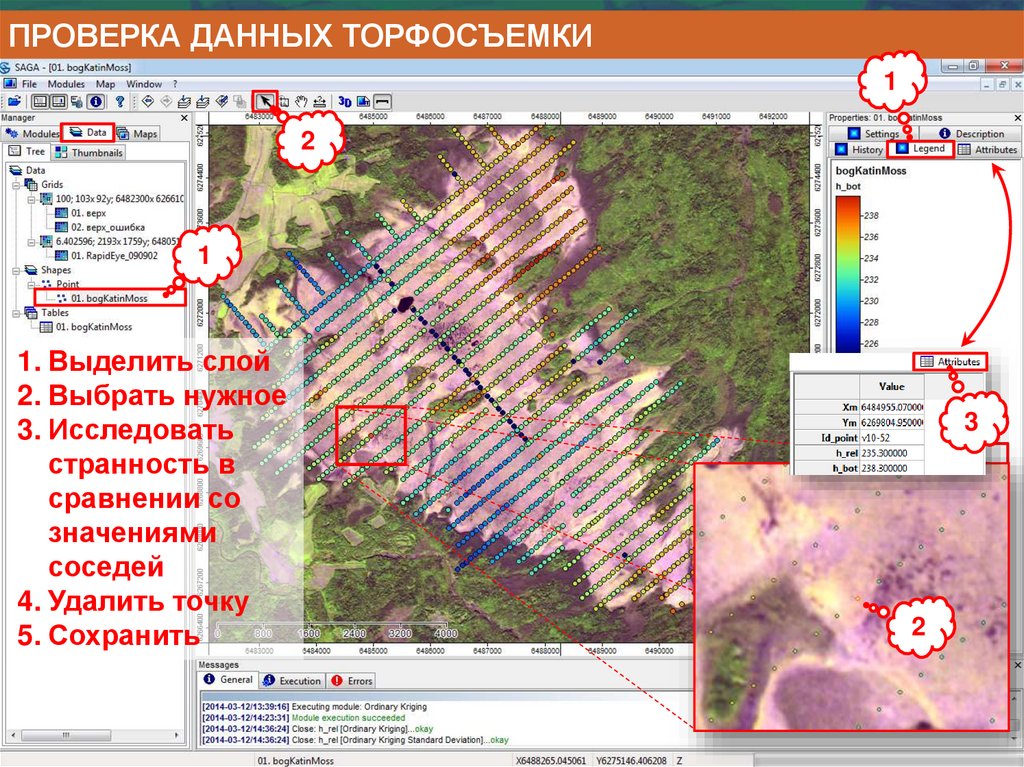
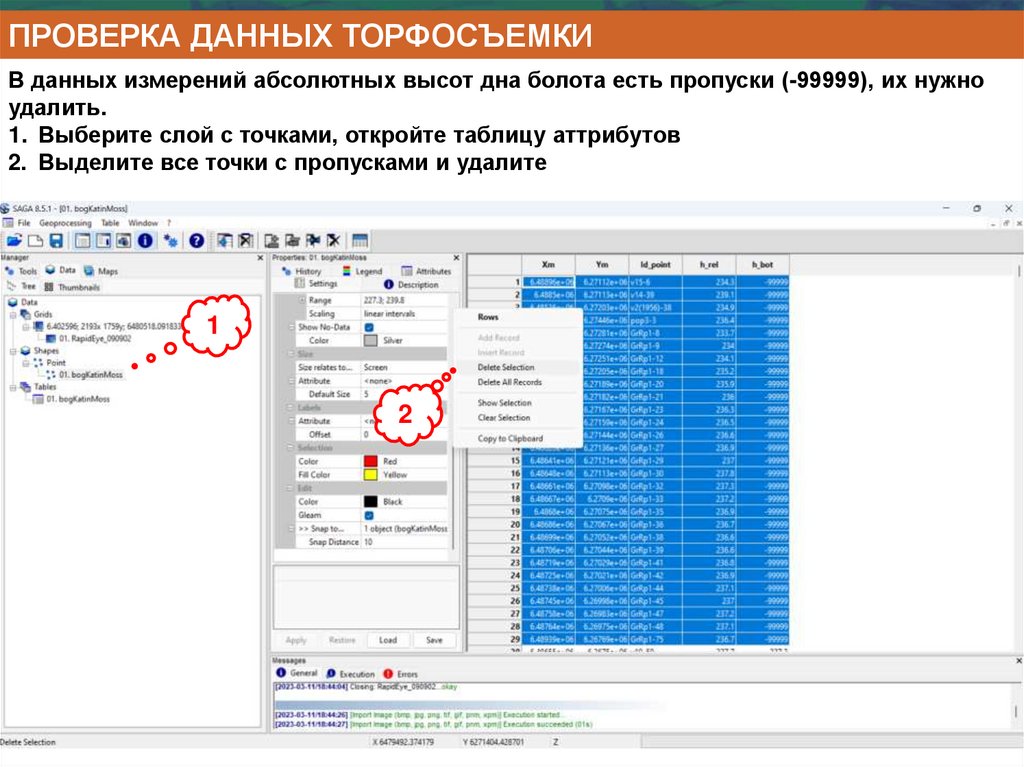
 Информатика
Информатика География
География








