Похожие презентации:
Функциональные возможности геоинформационных систем (ГИС)
1.
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОБРАБОТКИИ АНАЛИЗА ГЕОПРОСТРАНСТВЕННЫХ
ДАННЫХ НА ЭВМ
2.
Лекцию читаетк.т.н., доцент
БОБРОВА
ЛЮДМИЛА ВЛАДИМИРОВНА
3.
1. ФУНКЦИОНАЛЬНЫЕ ВОЗМОЖНОСТИ ГЕОИНФОРМАЦИОННЫХСИСТЕМ (ГИС)
Главное назначение ГИС
заключено в наборе
средств
создания и
объединения баз
данных
с возможностями их
географического анализа
и наглядной
визуализации в виде
различных карт,
графиков, диаграмм,
прямой привязке друг к
другу всех атрибутивных
и графических данных.
4.
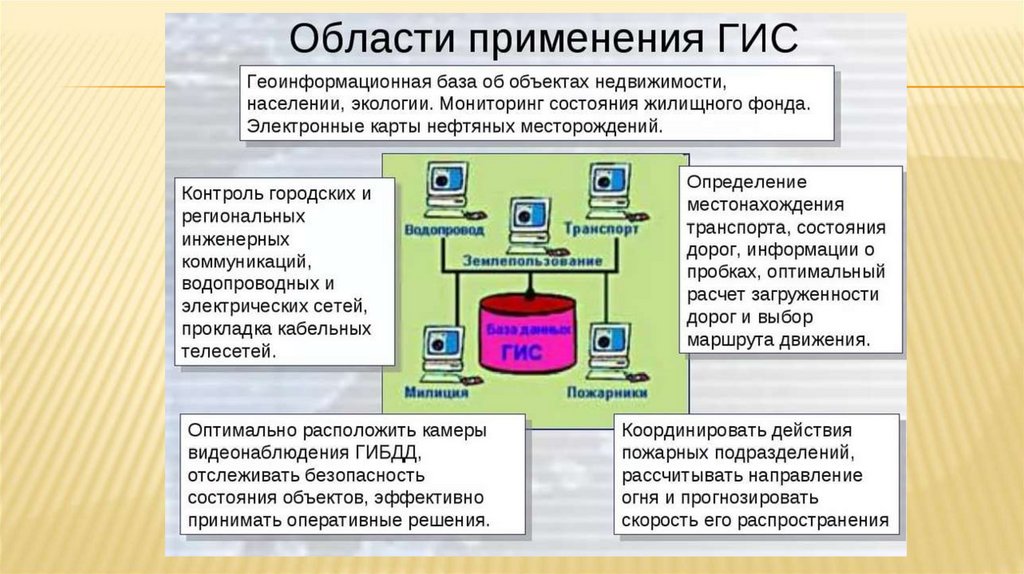
ГИС используются практически во всех областях современнойпромышленности и бизнеса, социальной инфраструктуры:
- для определения направления геологических и геодезических изысканий;
- для оптимального по разным критериям выбора местоположения новых
промышленных разработок, производственных мощностей, логистических
узлов;
- с целью поддержки принятия решений;
- для выбора кратчайших или наиболее безопасных маршрутов перевозок и
путей распределения продукции;
- в процессе анализа риска материальных вложений и урегулирования
разногласий;
- для демографических исследований, определения привязанного к
территории спроса на продукцию;
- при создании и географической привязке баз данных о земле и
домовладении.
5.
6.
ГИС объединяетсредства обычных
пакетов
картографического
отображения
с электронными
таблицами, базами и
хранилищами
данных.
7.
Виды ГИСГИС не являются серийным
продуктом, поскольку заказчик
не в состоянии с самого начала
точно представить себе все
задачи, которые ему предстоит
решать.
Фирмы – разработчики ГИС,
как правило, имеют для них
готовые модули,
обеспечивающие выполнение
одной из задач, например:
В процессе оформления заказа на
геоинформационную систему согласовывается
перечень модулей, необходимых конкретному
заказчику.
- поддержка устройств ввода и
вывода,
- работа с базами данных,
- визуализация и анализ данных.
8.
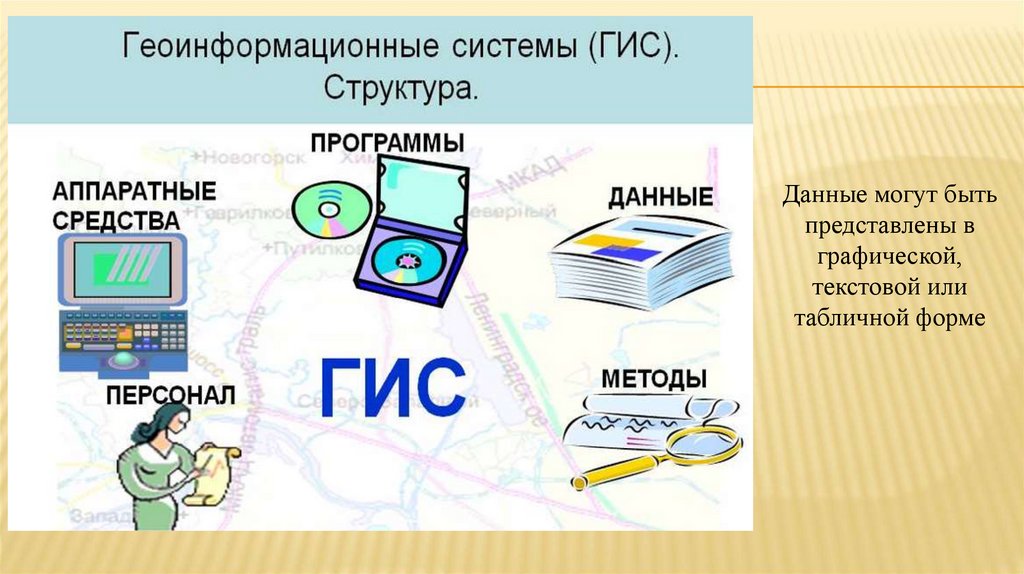
Данные могут бытьпредставлены в
графической,
текстовой или
табличной форме
9.
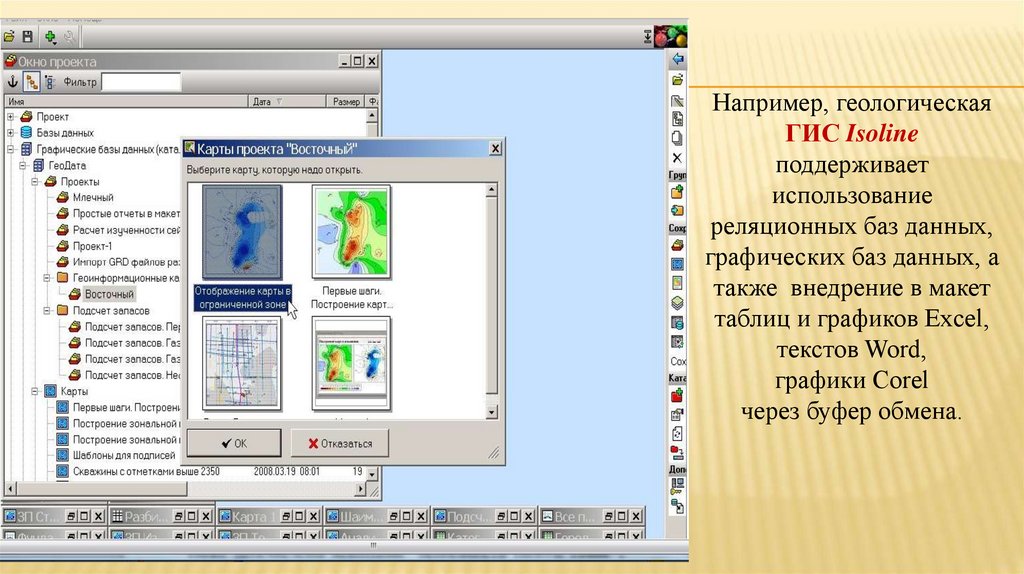
Например, геологическаяГИС Isoline
поддерживает
использование
реляционных баз данных,
графических баз данных, а
также внедрение в макет
таблиц и графиков Excel,
текстов Word,
графики Corel
через буфер обмена.
10.
Дигитайзер –устройство для
оцифровки
информации,
вводимой
пользователем
наложение
друг на друга
различных слоев,
представленных в
цифровой форме
11.
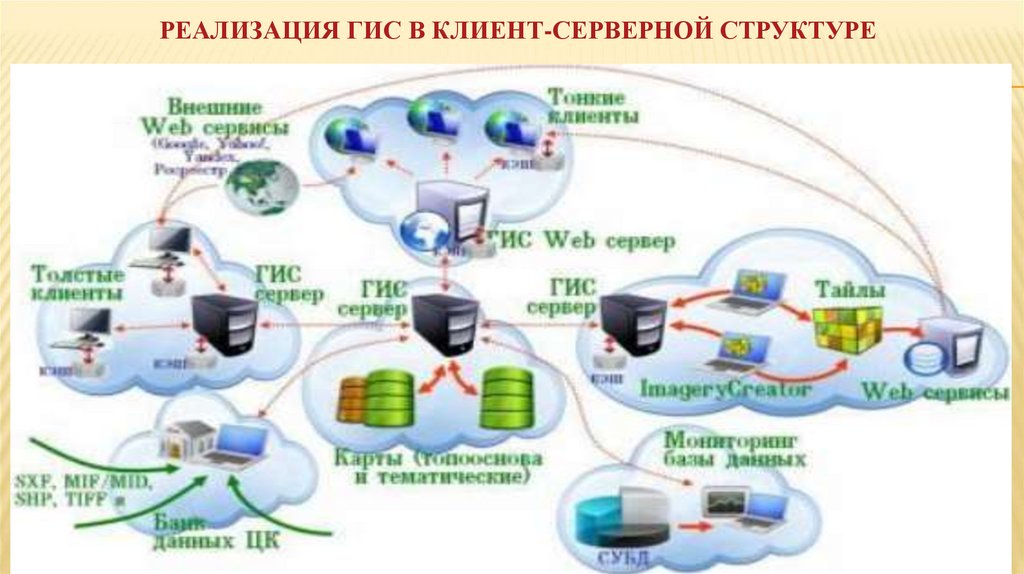
РЕАЛИЗАЦИЯ ГИС В КЛИЕНТ-СЕРВЕРНОЙ СТРУКТУРЕ12.
Программное обеспечение ГИС содержит инструментарий,необходимый для ввода, визуализации, анализа, преобразования,
хранения, а также вывода атрибутивной и пространственной
информации на какой-либо носитель (например, плоттер, принтер
или в другие системы).
Наиболее важными компонентами программных продуктов
являются:
• приборы для ввода и обработки пространственной информации;
• система управления базами данных;
• инструментарий поддержки SQL-запросов, анализа и визуализации
(отображения) информации;
• инструментарий статистического анализа данных;
• графический пользовательский интерфейс, обеспечивающий
доступ к инструментам и функциям.
13.
Результатом изучения дисциплины «Математические методыобработки и анализа геопространственных данных на ЭВМ» должно
стать:
- понимание роли и и места математических методов обработки и
анализа пространственных данных на ЭВМ;
- умение использовать численные методы для обработки и анализа
информации;
- умение осуществлять прогнозирование и установление связей между
процессами на основе анализа статистической информации;
- умение работать в среде Excel и MathCad для аналитического
представления взаимосвязи исследуемых процессов, описания
экспериментальных материалов и осуществления прогнозирования
(решать трансцендентные уравнения и системы, владеть методами
интерполяции и аппроксимации, регрессионного и корреляционного
анализа).
14.
2. ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ ЭКСПЕРИМЕНТАЛЬНЫХДАННЫХ
15.
16.
17.
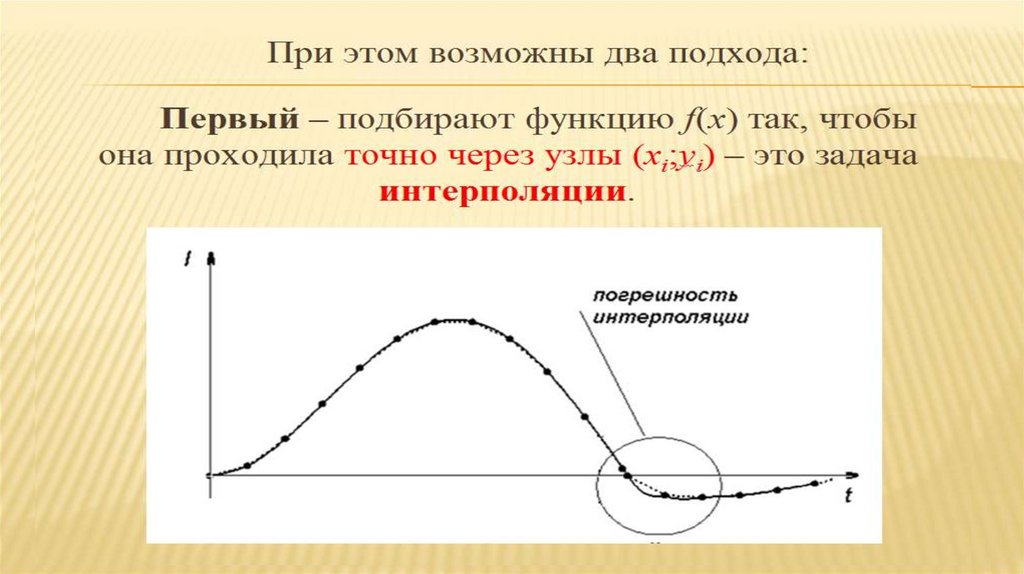
18.
2.1.1. Интерполяция функцийПусть функция
xi
yi
y=f(x) задана таблично
x0
x1
y0 f ( x0 ) y1 f ( x1 )
…
…
xn
yn f ( xn )
Требуется вычислить значения функции для
значений аргумента, не совпадающих с заданными в
таблице (между фиксированными значениями Х или
для прогнозных значений Х).
19.
Для этого неизвестную функцию f(x) заменяютфункцией F(x), аналитическое выражение которой
известно.
Эта функция называется
интерполирующей функцией,
а задача её нахождения –
задачей интерполяции.
xi
yi
x0
x1
y0 f ( x0 ) y1 f ( x1 )
…
…
xn
yn f ( xn )
20.
Задача интерполяции – по таблицеинтерполирующую функцию F ( x) f ( x )
x0 , x1 ,..., xn ;
xi
yi
- узлы интерполяции.
x0
x1
y0 f ( x0 ) y1 f ( x1 )
…
…
xn
yn f ( xn )
найти
21.
Таким образом, при интерполяции строится функцияF ( x) c1 1 ( x) c2 2 ( x) ... cm m ( x)
где c1 , c2 ,..., cm – числовые коэффициенты,
которые следует определить,
а
1 ( x), 2 ( x),..., m ( x)
– известные функции.
В качестве последних обычно используют
алгебраические или тригонометрические многочлены
и другие классы функций.
22.
Построим многочленPn ( x) a0 x a1 x
n
n 1
... an 1 x an
который будет интерполяционным, если его значения
совпадают со значениями заданной функции в узлах
интерполирования, т.е., если выполняется система из
равенств:
y0 f ( x0 ) Pn ( x0 )
y f (x ) P (x )
1
1
n
1
...............................
yn f ( xn ) Pn ( xn )
Задача состоит в вычислении коэффициентов
ai ( i 0,1,..., n )
интерполяционного многочлена.
23.
Линейная интерполяцияx0
x1
y0 = f(x0)
y1=f(x1)
Интерполяционный полином при n=1
P1 ( x) a0 a1 x
Система двух уравнений относительно неизвестных
a0, a1
y0 a0 a1 x0
y1 a0 a1 x1
24.
Решая систему, находим коэффициенты:y0 x1 x0 y0
a0
x1 x0
y1 y1
a1
x1 x0
После преобразований получаем интерполяционный
полином первой степени
P1 ( x)
x x1
x0 x1
y0
x x0
x1 x0
y1
25.
Квадратичная интерполяцияx0
x1
x2
y0 = f(x0)
y1=f(x1)
y2=f(x2)
Интерполяционный полином при n=2
P2 ( x) a0 a1 x a2 x
2
26.
Решаем систему трехнеизвестных a0, a1,a2
уравнений
относительно
y0 a0 a1 x0 ax02
y1 a0 a1 x1 ax
2
1
y 2 a0 a1 x2 ax
2
2
и получаем интерполяционный
полином второй степени:
( x x0 )( x x2 )
( x x0 )( x x1 )
( x x1 )( x x2 )
P2 ( x)
y0
y1
y2
( x0 x1 )( x0 x2 )
( x1 x0 )( x1 x2 )
( x2 x0 )( x2 x1 )
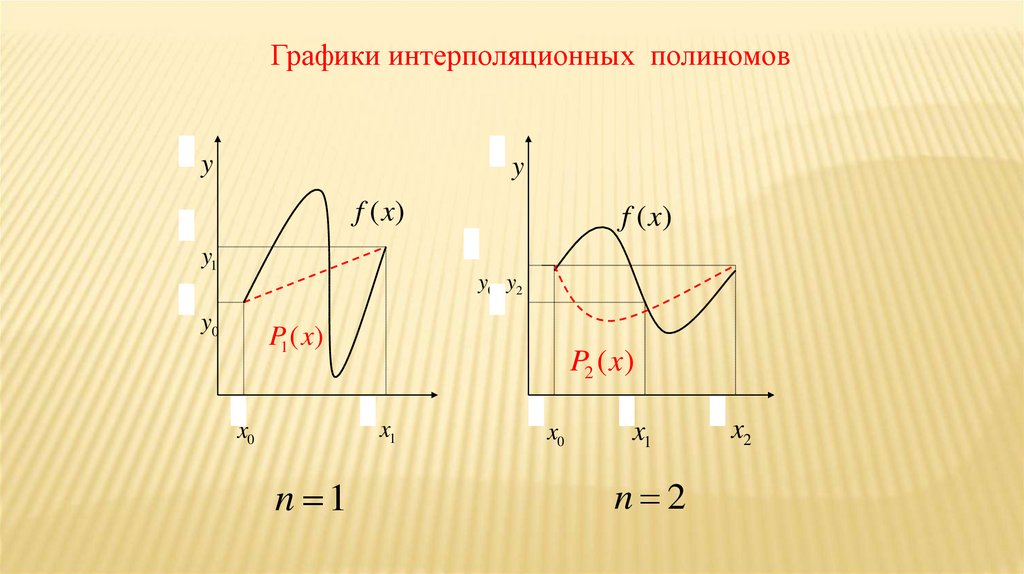
27.
Графики интерполяционных полиномовy
y
f ( x)
f ( x)
y1
y0 , y2
y0
P1 ( x)
P2 ( x)
x1
x0
n 1
x0
x1
n 2
x2
28.
Интерполяционный полином НьютонаКонечные разности
Рассмотрим случай, когда узлы интерполирования
равно отстоят друг от друга
x1 x0 x2 x1 ... xn xn 1 h
(h – шаг интерполяции).
Конечными разностями первого порядка называются
выражения
y0 y1 y0
y1 y2 y1
...................
yn 1 yn yn 1
29.
Конечные разности второго порядка:2 y0 y1 y0 y2 2 y1 y0
y1 y2 y1 y3 2 y2 y1
2
.................................................
2 yn 2 yn 1 yn 2 yn 2 yn 1 yn 2
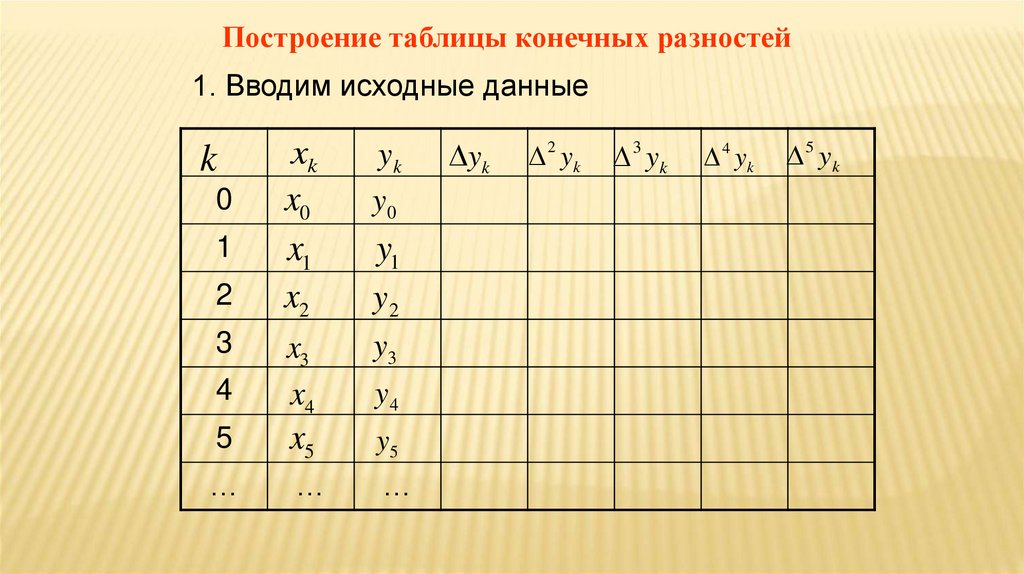
30.
Построение таблицы конечных разностей1. Вводим исходные данные
0
xk
x0
yk
y0
1
x1
2
x2
y1
y2
3
4
x3
x4
y3
y4
5
x5
y5
…
…
…
k
y k
2 yk
3 yk
4 yk
5 yk
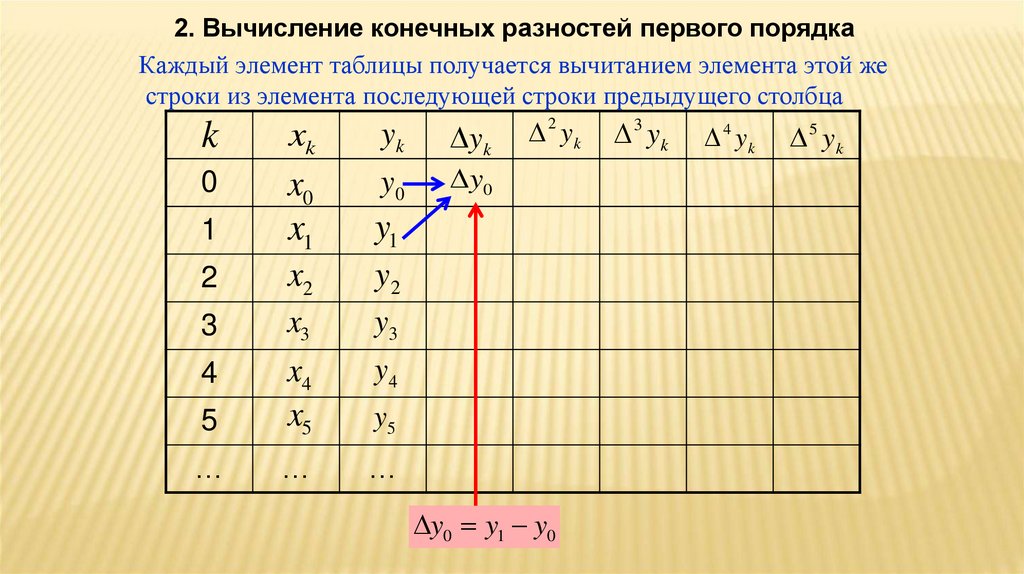
31.
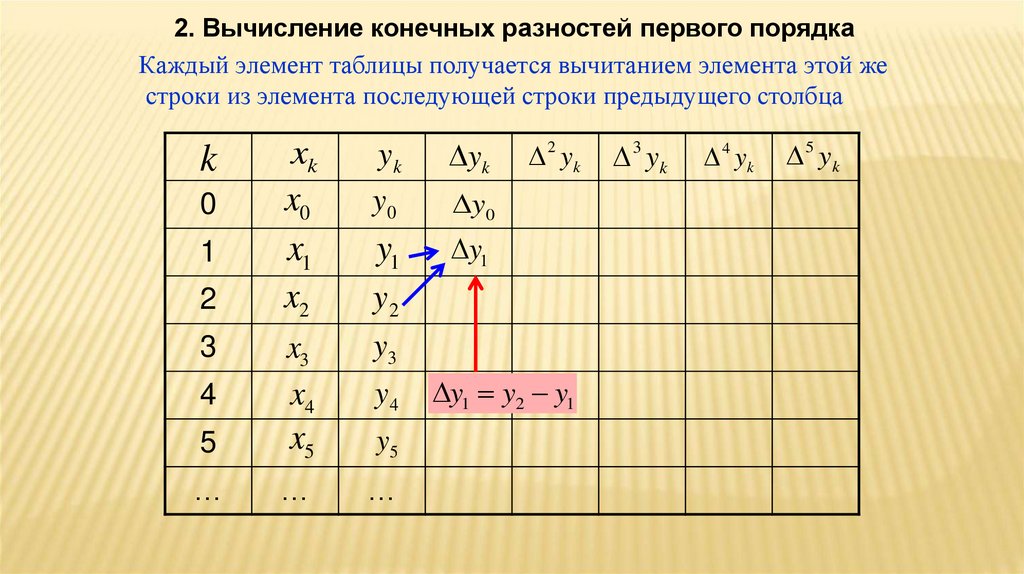
2. Вычисление конечных разностей первого порядкаКаждый элемент таблицы получается вычитанием элемента этой же
строки из элемента последующей строки предыдущего столбца
k
0
xk
x0
yk
y0
1
x1
2
x2
y1
y2
3
x3
4
5
x4
x5
y5
…
…
…
y k
2 yk
y0
y3
y4
y0 y1 y0
3 yk
4 yk
5 yk
32.
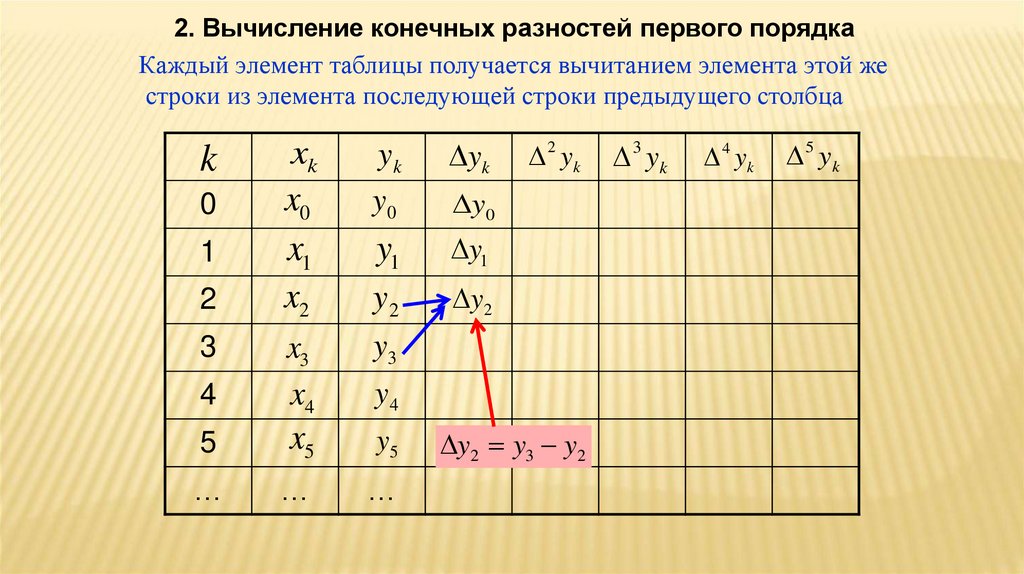
2. Вычисление конечных разностей первого порядкаКаждый элемент таблицы получается вычитанием элемента этой же
строки из элемента последующей строки предыдущего столбца
yk
y0
y k
0
xk
x0
1
x1
y1
2
x2
y1
y2
3
4
x3
x4
y3
y4
5
x5
y5
…
…
…
k
2 yk
y0
y1 y2 y1
3 yk
4 yk
5 yk
33.
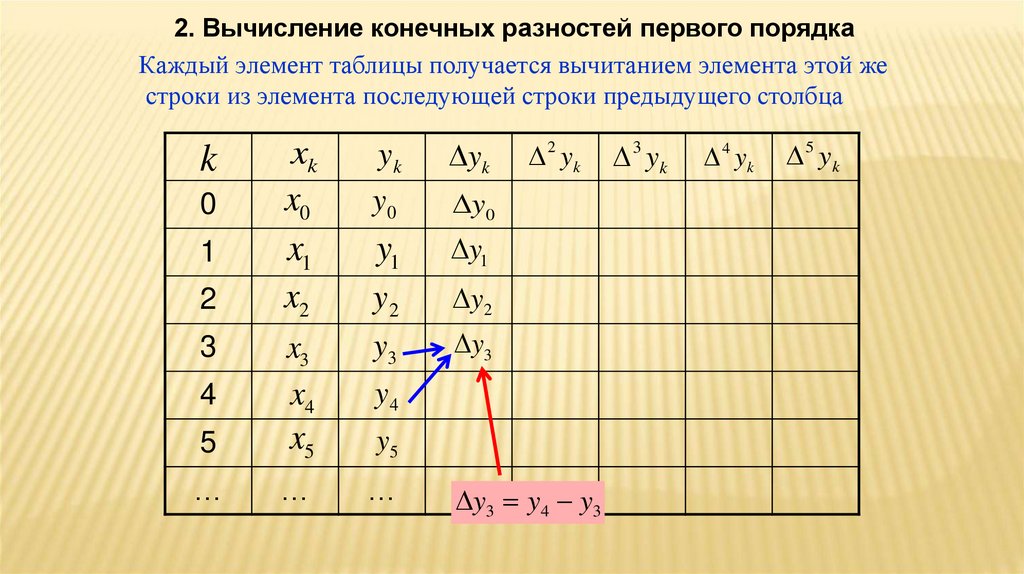
2. Вычисление конечных разностей первого порядкаКаждый элемент таблицы получается вычитанием элемента этой же
строки из элемента последующей строки предыдущего столбца
yk
y0
y k
0
xk
x0
1
x1
y1
2
x2
y1
y2
3
4
x3
x4
y3
y4
5
x5
y5
…
…
…
k
2 yk
y0
y 2
y2 y3 y2
3 yk
4 yk
5 yk
34.
2. Вычисление конечных разностей первого порядкаКаждый элемент таблицы получается вычитанием элемента этой же
строки из элемента последующей строки предыдущего столбца
yk
y0
y k
0
xk
x0
1
x1
y1
2
x2
y1
y2
3
y3
y4
y3
4
x3
x4
5
x5
y5
…
…
…
k
2 yk
y0
y 2
y3 y4 y3
3 yk
4 yk
5 yk
35.
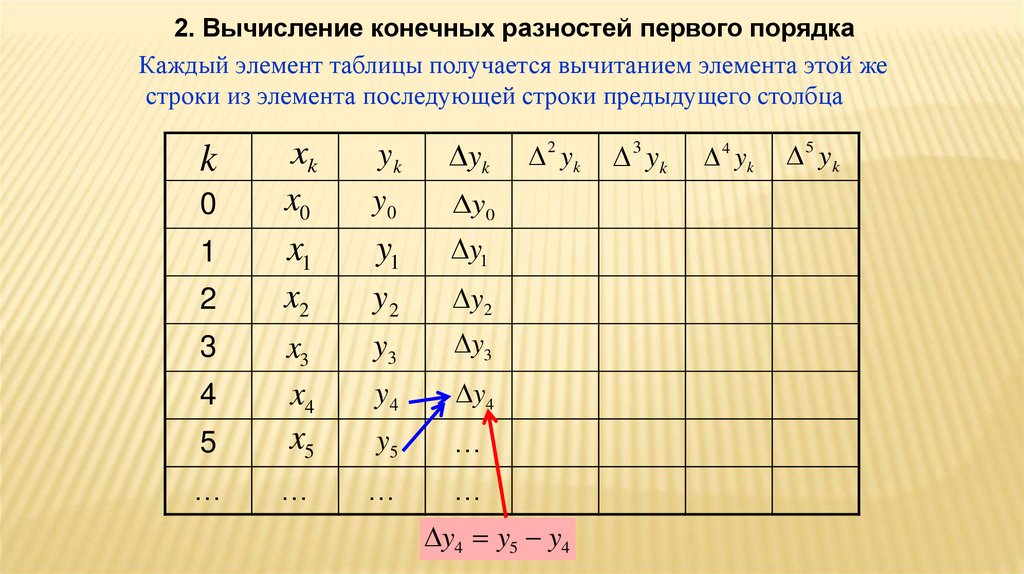
2. Вычисление конечных разностей первого порядкаКаждый элемент таблицы получается вычитанием элемента этой же
строки из элемента последующей строки предыдущего столбца
yk
y0
y k
0
xk
x0
1
x1
y1
2
x2
y1
y2
3
y3
y4
y3
4
x3
x4
5
x5
y5
…
…
…
…
…
k
2 yk
y0
y 2
y 4
y4 y5 y4
3 yk
4 yk
5 yk
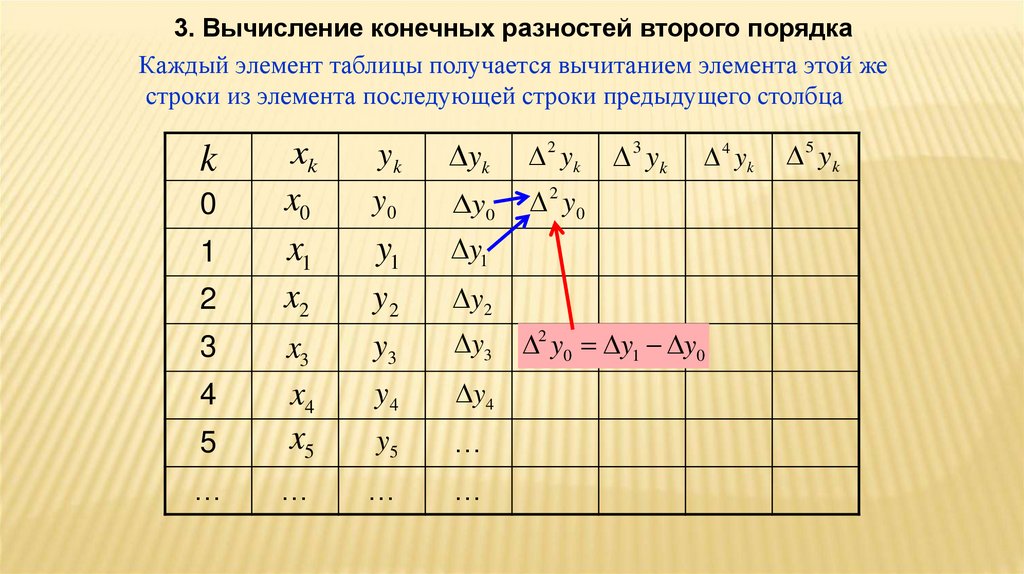
36.
3. Вычисление конечных разностей второго порядкаКаждый элемент таблицы получается вычитанием элемента этой же
строки из элемента последующей строки предыдущего столбца
yk
y0
y k
2 yk
0
xk
x0
y0
2 y0
1
x1
y1
2
x2
y1
y2
3
y3
y4
y3
4
x3
x4
5
x5
y5
…
…
…
…
…
k
3 yk
4 yk
y 2
y 4
2 y0 y1 y0
5 yk
37.
3. Вычисление конечных разностей второго порядкаКаждый элемент таблицы получается вычитанием элемента этой же
строки из элемента последующей строки предыдущего столбца
yk
y0
y k
2 yk
0
xk
x0
y0
2 y0
1
x1
y1
2 y1
2
x2
y1
y2
3
y3
y4
y3
4
x3
x4
5
x5
y5
…
…
…
…
…
k
3 yk
4 yk
y 2
y 4
2 y1 y2 y1
5 yk
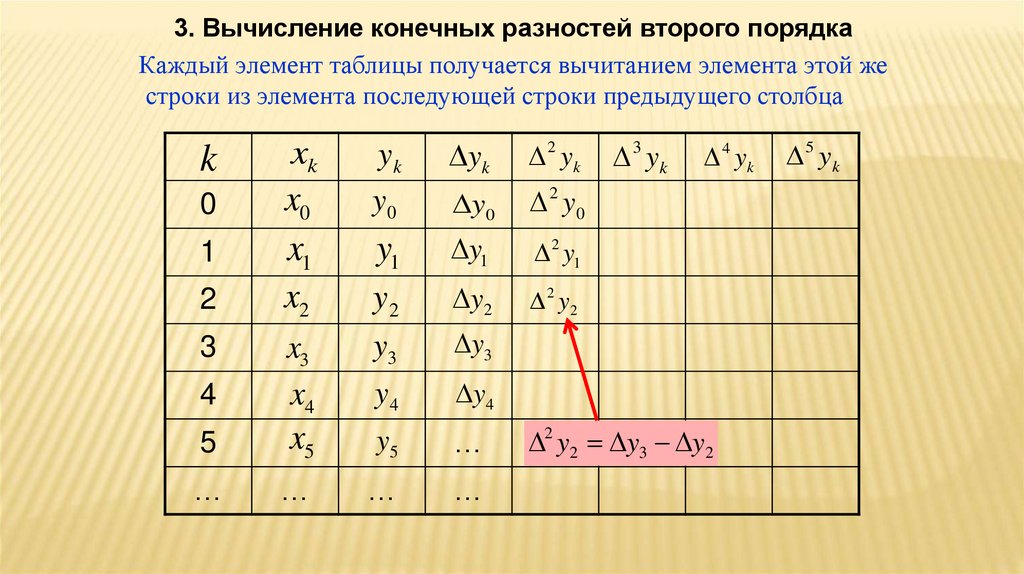
38.
3. Вычисление конечных разностей второго порядкаКаждый элемент таблицы получается вычитанием элемента этой же
строки из элемента последующей строки предыдущего столбца
yk
y0
y k
2 yk
0
xk
x0
y0
2 y0
1
x1
y1
2 y1
2
x2
y1
y2
y 2
2 y2
3
y3
y4
y3
4
x3
x4
5
x5
y5
…
…
…
…
…
k
3 yk
4 yk
y 4
2 y2 y3 y2
5 yk
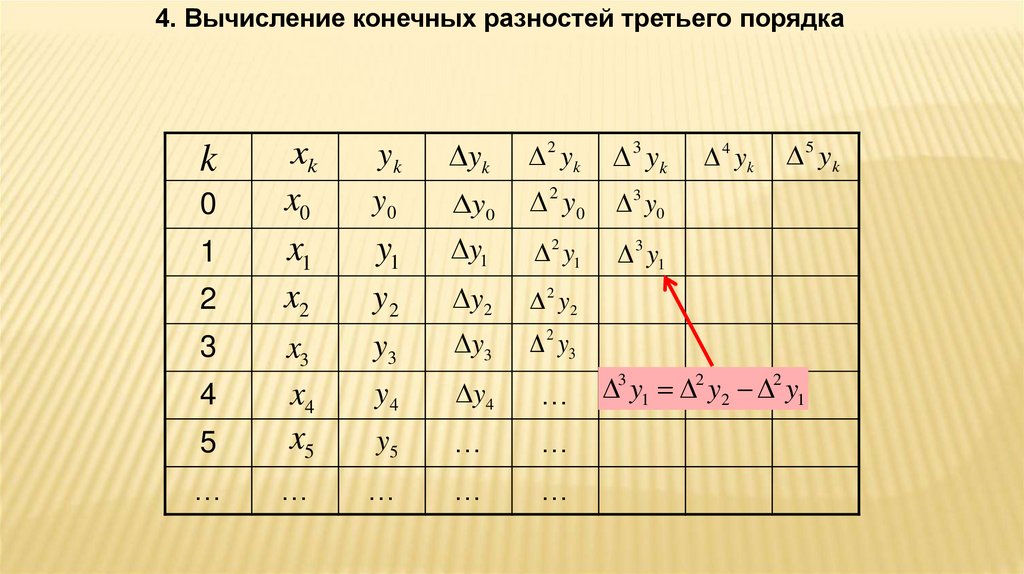
39.
4. Вычисление конечных разностей третьего порядкаyk
y0
y k
2 yk
3 yk
0
xk
x0
y0
2 y0
3 y0
1
x1
y1
2 y1
2
x2
y1
y2
y 2
2 y2
y3
y4
2 y3
4
x3
x4
y3
y 4
…
5
x5
y5
…
…
…
…
…
…
…
k
3
4 yk
5 yk
3 y0 2 y1 2 y0
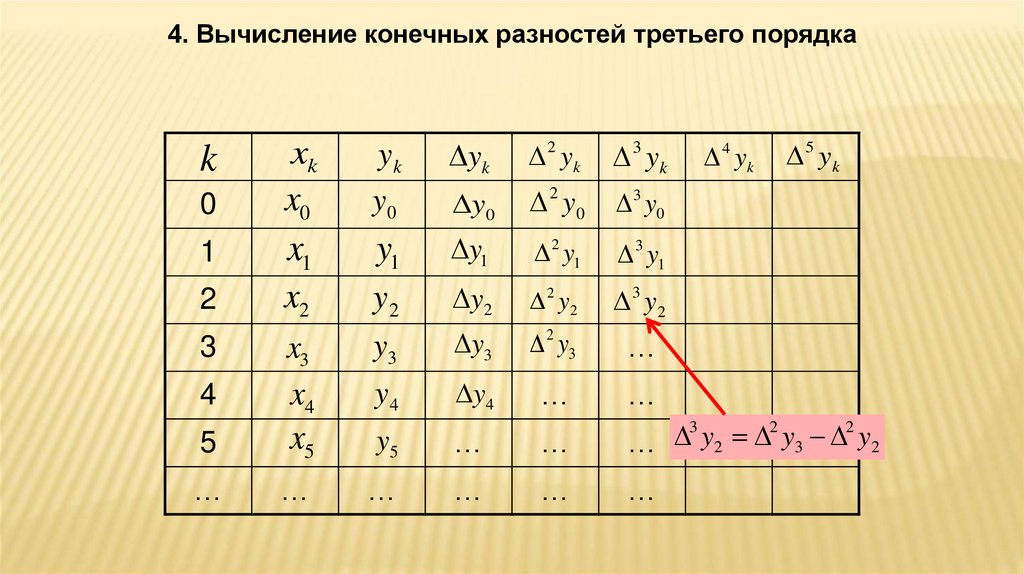
40.
4. Вычисление конечных разностей третьего порядкаyk
y0
y k
2 yk
3 yk
0
xk
x0
y0
2 y0
3 y0
1
x1
y1
2 y1
3 y1
2
x2
y1
y2
y 2
2 y2
y3
y4
2 y3
4
x3
x4
y3
y 4
…
5
x5
y5
…
…
…
…
…
…
…
k
3
4 yk
5 yk
3 y1 2 y2 2 y1
41.
4. Вычисление конечных разностей третьего порядкаyk
y0
y k
2 yk
3 yk
0
xk
x0
y0
2 y0
3 y0
1
x1
y1
2 y1
3 y1
2
x2
y1
y2
y 2
2 y2
3 y2
x3
x4
y3
y4
y3
2 y3
…
y 4
…
…
5
x5
y5
…
…
3
2
2
y
y
y2
2
3
…
…
…
…
…
…
…
k
3
4
4 yk
5 yk
42.
5. Вычисление конечных разностей четвертого порядкаyk
y0
y k
2 yk
3 yk
4 yk
0
xk
x0
y0
2 y0
3 y0
4 y0
1
x1
y1
2 y1
3 y1
2
x2
y1
y2
y 2
2 y2
3 y2
y3
y4
2 y3
4
x3
x4
y3
y 4
…
… 4 y0 3 y1 3 y0
…
5
x5
y5
…
…
…
…
…
…
…
…
…
k
3
5 yk
43.
5. Вычисление конечных разностей четвертого порядкаyk
y0
y k
2 yk
3 yk
4 yk
0
xk
x0
y0
2 y0
3 y0
4 y0
1
x1
y1
2 y1
3 y1
4 y1
2
x2
y1
y2
y 2
2 y2
3 y2
…
y3
y4
2 y3
…
…
4
x3
x4
y3
y 4
…
…
…
5
x5
y5
…
…
…
…
…
…
…
…
…
…
…
k
3
5 yk
4 y1 3 y2 3 y1
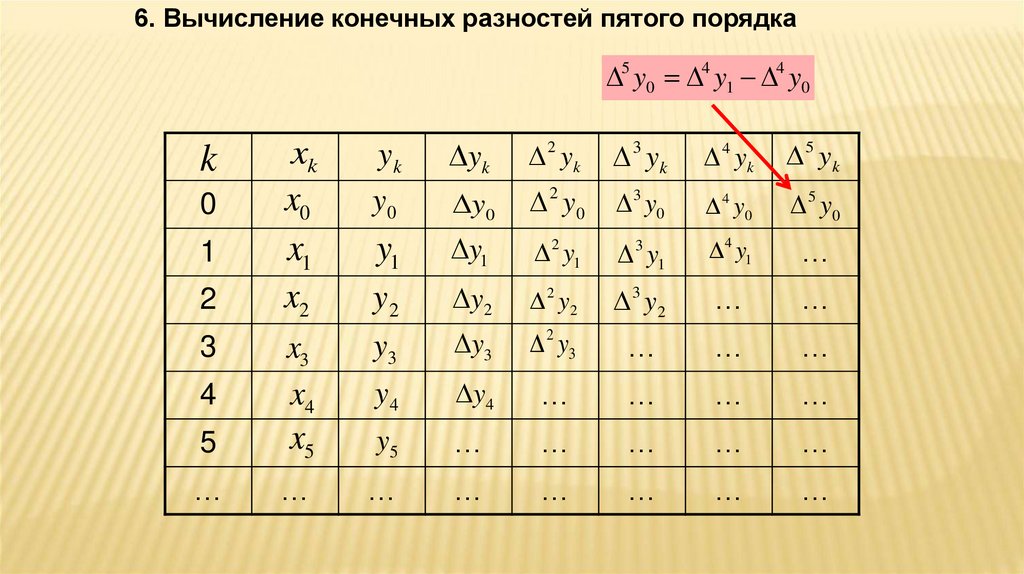
44.
6. Вычисление конечных разностей пятого порядка5 y0 4 y1 4 y0
yk
y0
y k
2 yk
3 yk
4 yk
5 yk
0
xk
x0
y0
2 y0
3 y0
4 y0
5 y0
1
x1
y1
2 y1
3 y1
4 y1
…
2
x2
y1
y2
y 2
2 y2
3 y2
…
…
y3
y4
2 y3
…
…
…
4
x3
x4
y3
y 4
…
…
…
…
5
x5
y5
…
…
…
…
…
…
…
…
…
…
…
…
…
k
3
45.
Интерполяционный полином Ньютонаk y0
Pn ( x) y0 ( x x0 )( x x1 ) ( x xk 1 )
k
k!h
k 1
n
h – шаг интерполяции (расстояние между двумя значениями Х;
k! = 1* 2 * 3 *4*…*n
Погрешность при замене функции полиномом
Ньютона:
n y0
R ( x) ( x x0 )( x x1 )...( x xn 1 )
n!h n
46.
ПримерФункция y f ( x) задана таблицей:
x
y
0
5
1
5
2 3
9 25
Необходимо вычислить значения функции в точках
х=0,3 и х=0,5
Решение
1. Вычисляем конечные разности:
Первого порядка:
y0 y1 y0 5 5 0
y1 y2 y1 9 5 4
47.
Самостоятельная работаЗадание. Найти следующую конечную
разность первого порядка
Варианты
A. 8
ответов:
В. 2
С. 16
D. 6
y0 y1 y0 5 5 0
x
0
1
2
3
y1 y2 y1 9 5 4
y
5
5
9 25
48.
СВЕРИМ ОТВЕТЫ?y0 y1 y0 5 5 0
y1 y2 y1 9 5 4
y2 y3 y2 25 9 16
Номер
0
1
2
3
x
0
1
2
3
y
5
5
9
25
49.
2. Заносим конечные разности первого порядкатаблицу:
y k y k 3 y k
2
k
xk
yk
0
0
5
0
1
1
5
4
2
2
9
16
3
3
25
y0 y1 y0 5 5 0
y1 y2 y1 9 5 4
y2 y3 y2 25 16
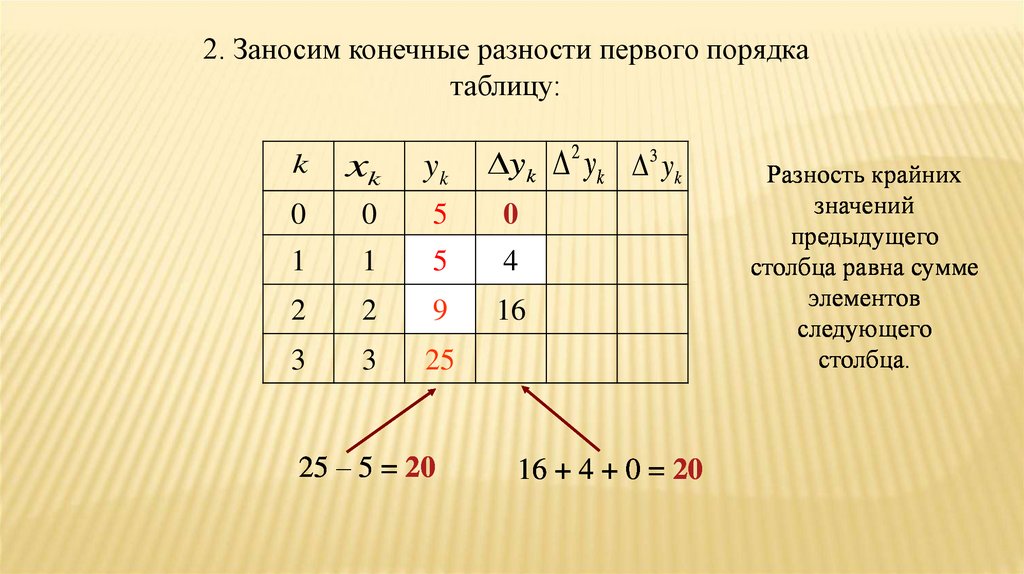
50.
2. Заносим конечные разности первого порядкатаблицу:
y k y k 3 y k
2
k
xk
yk
0
0
5
0
1
1
5
4
2
2
9
16
3
3
25
25 – 5 = 20
16 + 4 + 0 = 20
Разность крайних
значений
предыдущего
столбца равна сумме
элементов
следующего
столбца.
51.
3. Находим конечные разности второго порядка:2 y0 y1 y0 4 0 4
y k y k y k y k
2
k
xk
0
0
5
0
1
1
5
4
2
2
9
16
3
3
25
3
52.
Самостоятельная работаНайдите следующую конечную разность второго порядка.
y k y k 2 y k 3 y k
k
xk
0
0
5
0
1
1
5
4
2
2
9
16
3
3
25
4
2 y0 y1 y0 4 0 4
53.
3. Находим конечные разности второго порядка:y1 y2 y1 16 4 12
2
y k y k 2 y k 3 y k
k
xk
0
0
5
0
1
1
5
4
2
2
9
16
3
3
25
4
2 y0 y1 y0 4 0 4
54.
3. Заносим конечные разности второго порядка:в таблицу:
y k y k 2 y k 3 y k
k
xk
0
0
5
0
4
1
1
5
4
12
2
2
9
16
3
3
25
2 y0 y1 y0 4 0 4
2 y1 y2 y1 16 4 12
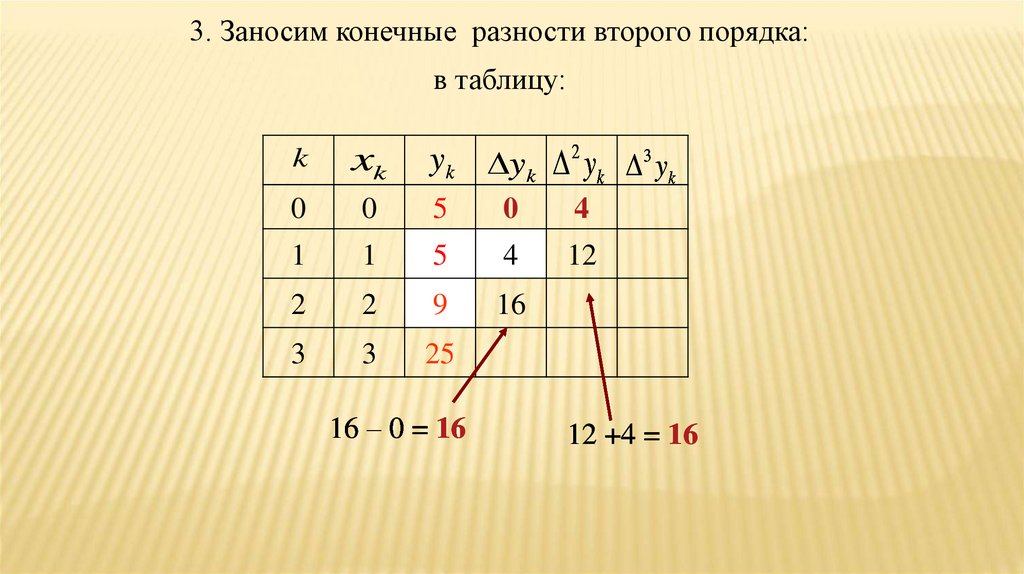
55.
3. Заносим конечные разности второго порядка:в таблицу:
y k y k 2 y k 3 y k
k
xk
0
0
5
0
4
1
1
5
4
12
2
2
9
16
3
3
25
16 – 0 = 16
12 +4 = 16
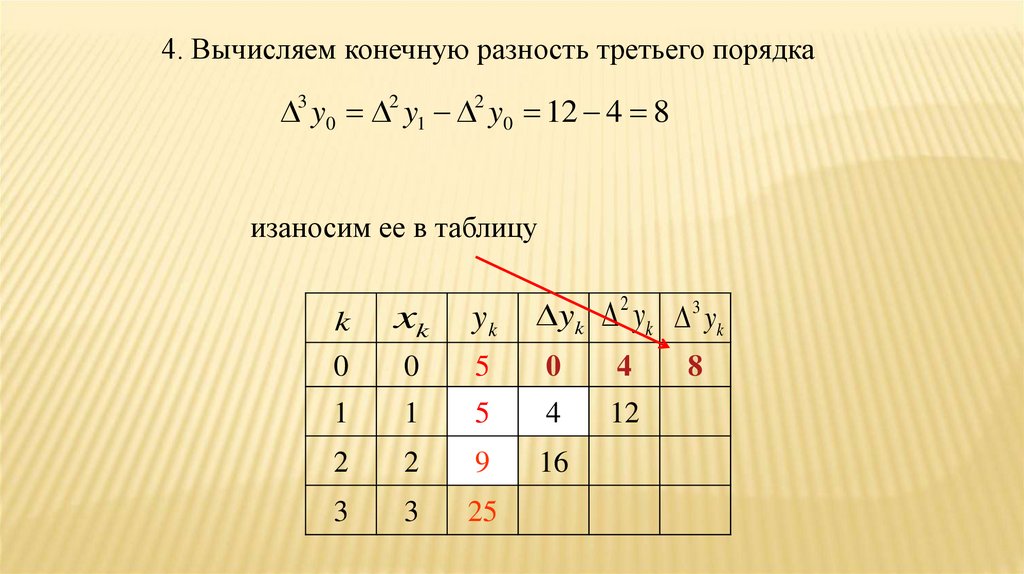
56.
4. Вычисляем конечную разность третьего порядка3 y0 2 y1 2 y0 12 4 8
изаносим ее в таблицу
y k y k 3 y k
2
k
xk
yk
0
0
5
0
4
1
1
5
4
12
2
2
9
16
3
3
25
8
57.
5. Составляеминтерполяционный
полином Ньютона:
y k y k 2 y 3 y
k
k
k
xk
0
0
5
0
4
1
1
5
4
12
2
2
9
16
3
3
25
8
( x 0) 0 ( x 0)( x 1) 4 ( x 0)( x 1)( x 2) 8
2
3
1 1
1
1 2
1
1 2 3
4
4
2
(2)
5 0 2 x( x 1) x( x 1)( x 2) x 3 2 x 2 x 5
3
3
3
P3 ( x) 5
x x0 y0 ( x x0 )( x x1 ) 2 y0 ( x x0 )( x x1 )( x x2 ) 3 y0
Pn ( x) P3 ( x) y0
2
h 1!
h
2!
h3
3!
(1)
58.
6. Вычисляем значения функции, заданной таблицей вточках x 0.3 и x 0.5
Для этого подставляем данные значения в выражение (2):
2
4
2
P3 (0,3) 5 0,3 2 (0,3) (0,3)3 5,056
3
3
2
4
2
P3 (0,5) 5 0,5 2 (0,5) (0,5)3 5,000
3
3
4 3
2
2
P3 ( x) x 2 x x 5
3
3
(2)
59.
Экстраполяция - прогнозированиеОсуществить прогноз значения y при x=4.
4 3
2
2
P3 ( x 4) 4 2 4 4 5
3
3
4 3
2
2
P3 ( x ) x 2 x x 5 (2)
3
3
60.
Экстраполяция - прогнозированиеОсуществить прогноз значения y при x=4.
4 3
2
4
8
2
P3 ( x 4) 4 2 4 4 5 64 32 5
3
3
3
3
4 3
2
2
P3 ( x ) x 2 x x 5 (2)
3
3
61.
Экстраполяция - прогнозированиеОсуществить прогноз значения y при x=4.
4 3
2
4
8
2
P3 ( x 4) 4 2 4 4 5 64 32 5
3
3
3
3
256 8
264 81 187
27
62,3
3
3
3
4 3
2
2
P3 ( x ) x 2 x x 5 (2)
3
3
62.
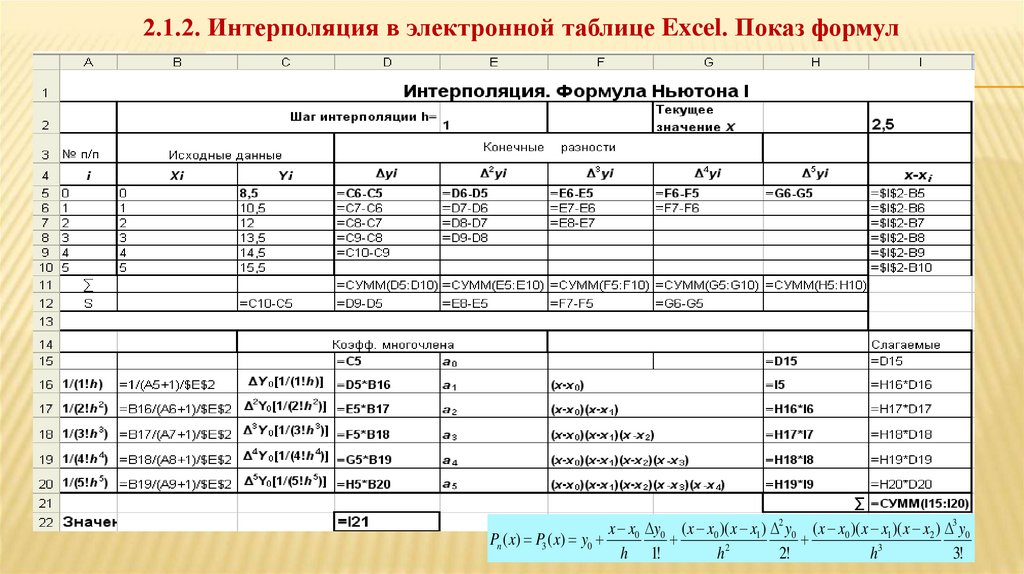
2.1.2. Интерполяция в электронной таблице Excel. Показ формулx x0 y0 ( x x0 )( x x1 ) 2 y0 ( x x0 )( x x1 )( x x2 ) 3 y0
Pn ( x) P3 ( x) y0
h 1!
h2
2!
h3
3!
63.
Интерполяция в электронной таблице Excel. Показ вычисленийx x0 y0 ( x x0 )( x x1 ) 2 y0 ( x x0 )( x x1 )( x x2 ) 3 y0
Pn ( x) P3 ( x) y0
h 1!
h2
2!
h3
3!
64.
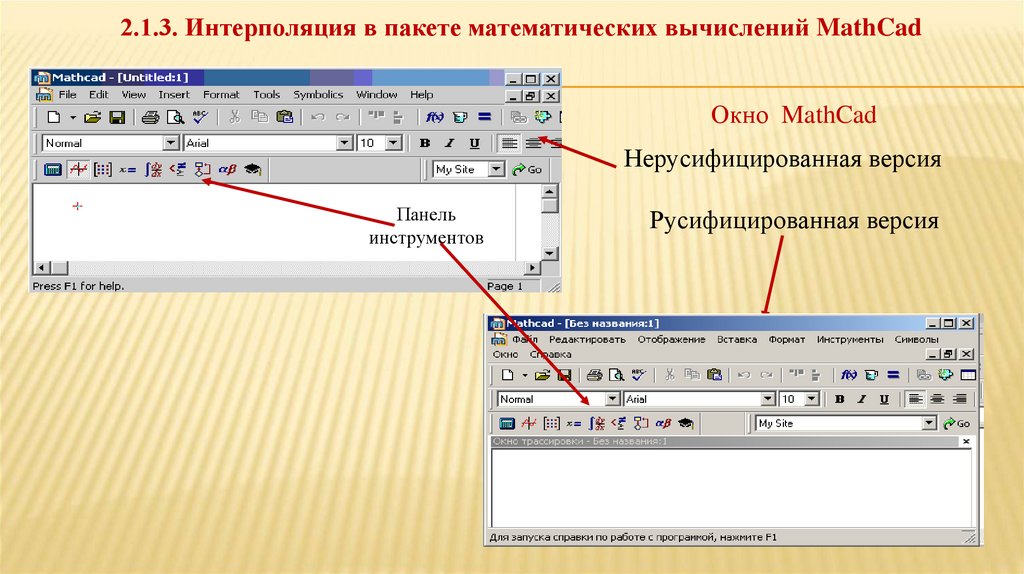
2.1.3. Интерполяция в пакете математических вычислений MathCadОкно MathCad
Нерусифицированная версия
Панель
инструментов
Русифицированная версия
65.
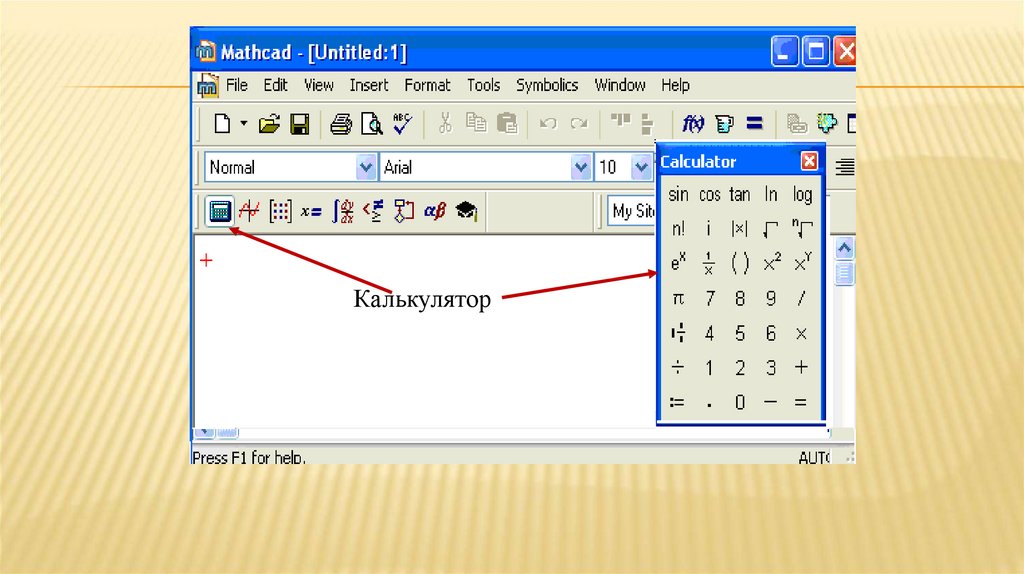
Калькулятор66.
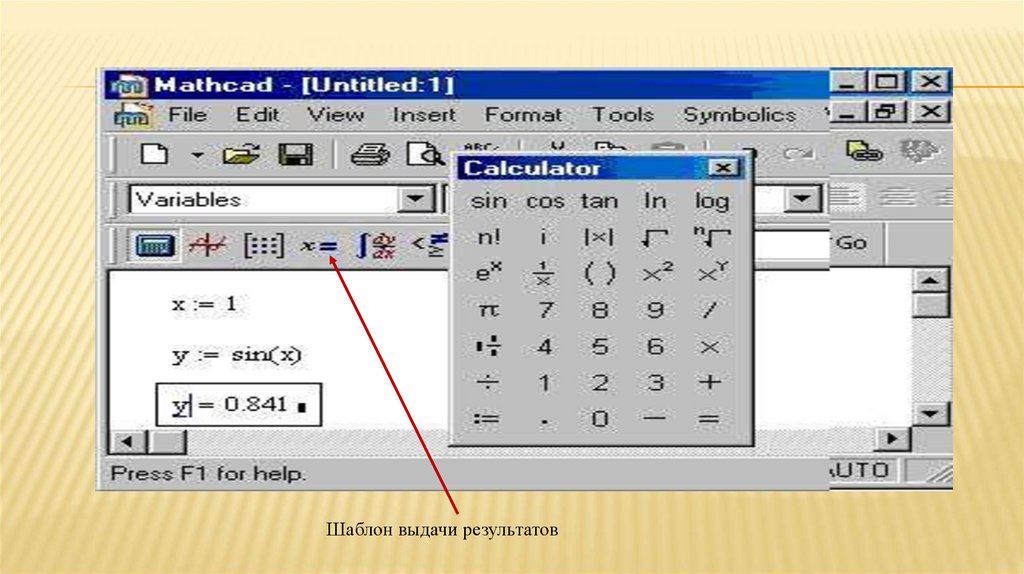
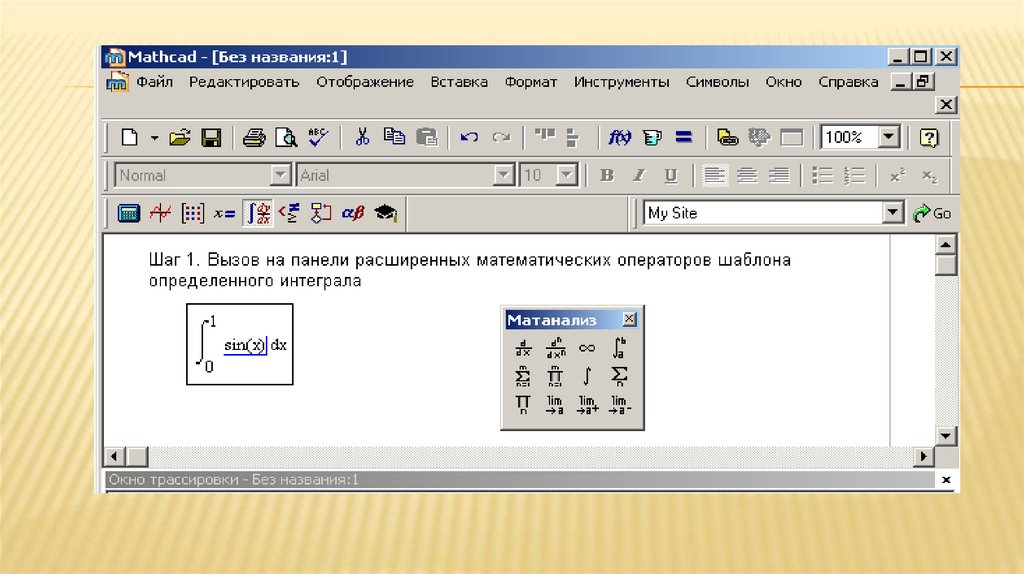
Шаблон выдачи результатов67.
Шаблон матриц68.
69.
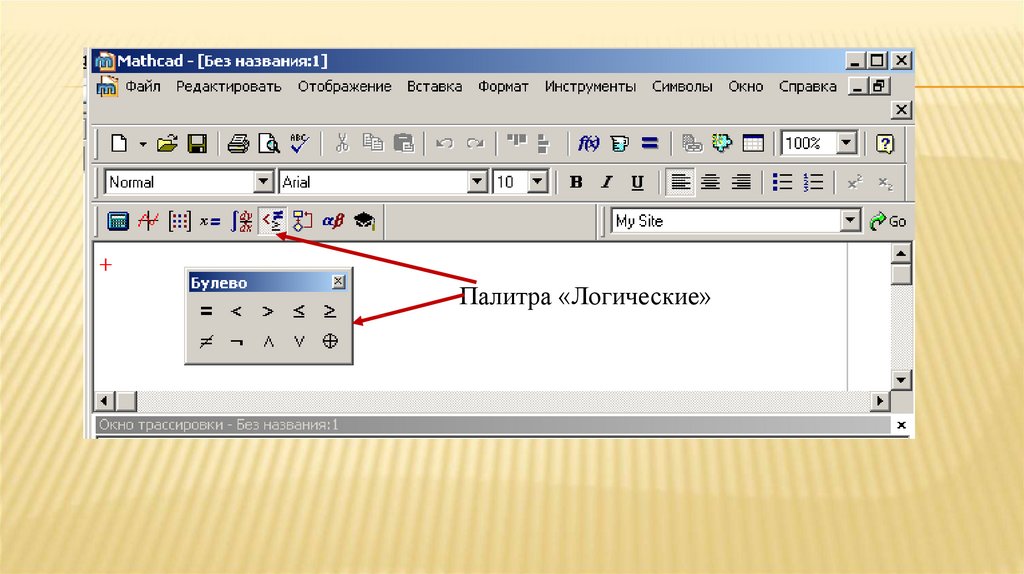
Палитра «Логические»70.
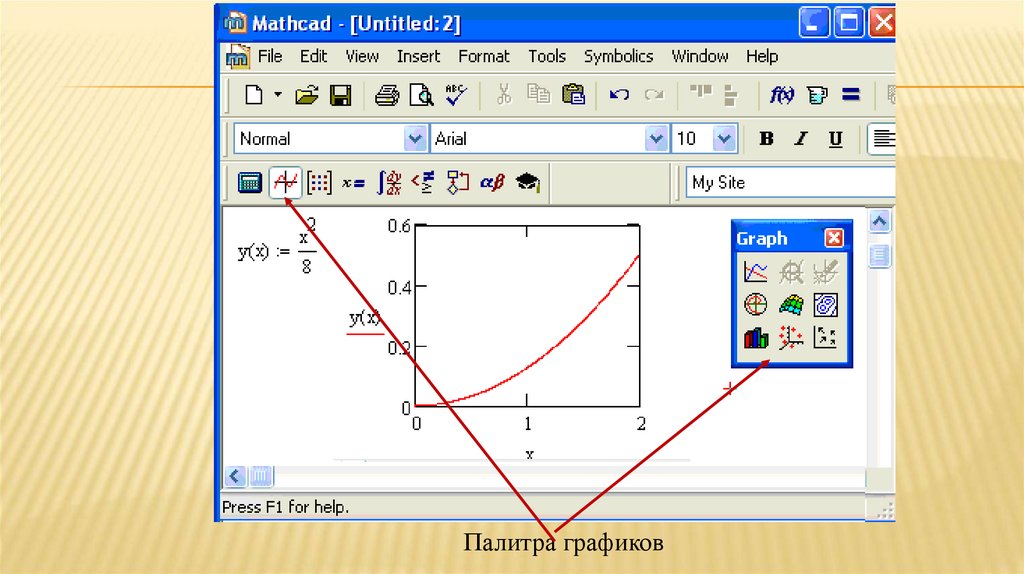
Палитра графиков71.
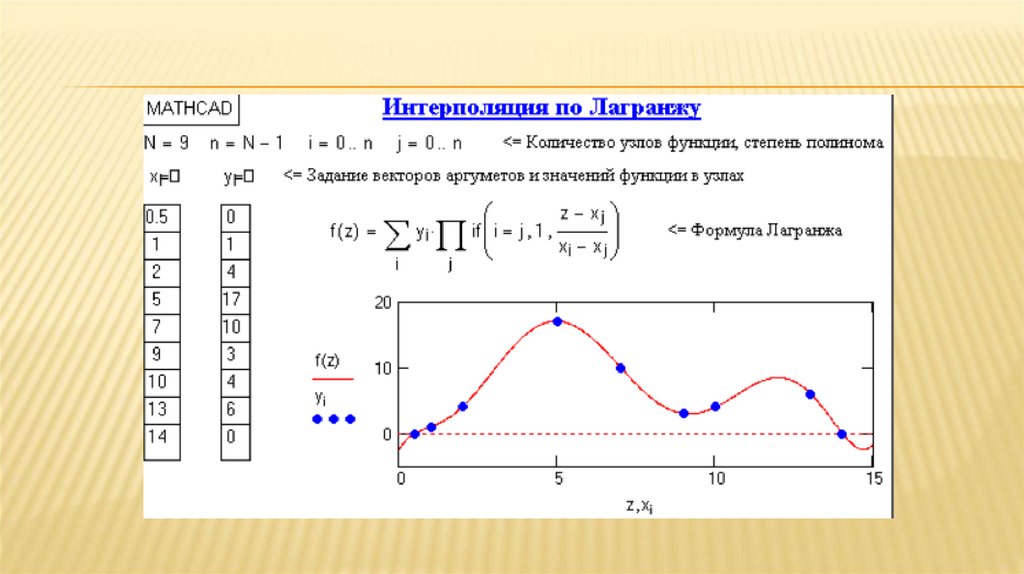
Интерполяция в MathCad72.
73.
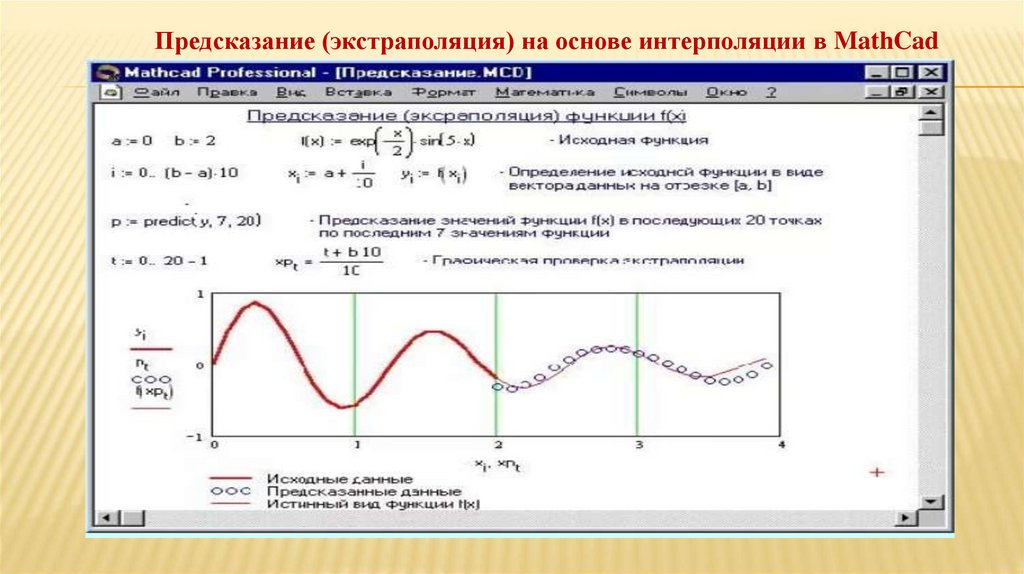
Предсказание (экстраполяция) на основе интерполяции в MathCad74.
2.2. АППРОКСИМАЦИЯ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ.РЕГРЕССИОННЫЕ МОДЕЛИ
75.
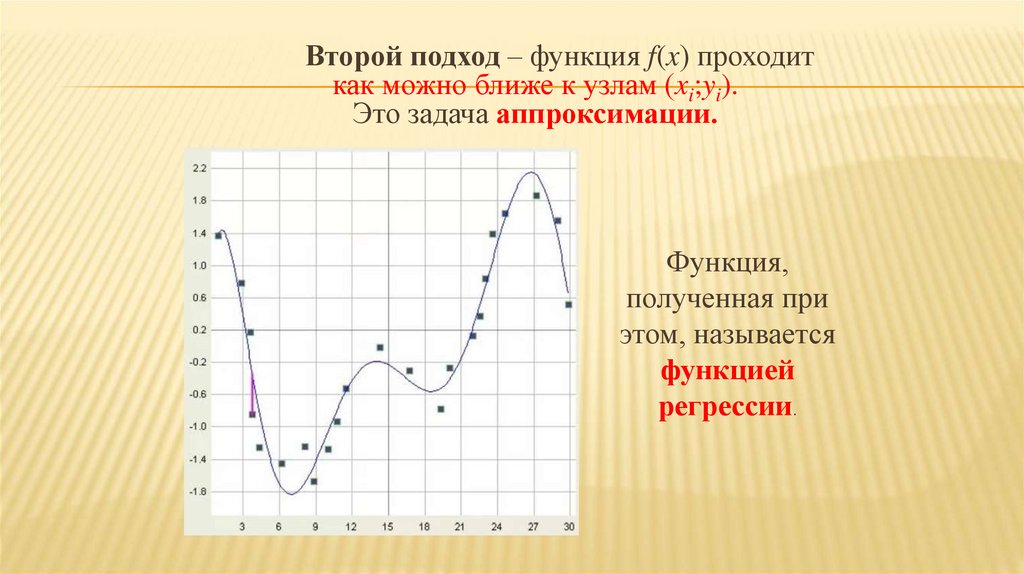
Второй подход – функция f(x) проходиткак можно ближе к узлам (xi;yi).
Это задача аппроксимации.
Функция,
полученная при
этом, называется
функцией
регрессии.
76.
Если связь между переменными х иу линейная, регрессия называется
линейной.
Если переменные связаны нелинейным
образом, регрессия будет нелинейной.
При линейной связи между переменными,
уравнение регрессии имеет вид
y = b0 + b1x.
Коэффициенты b0 и b1 называются
коэффициентами регрессии.
77.
Если рассматривается зависимостьмежду двумя переменными х и у,
регрессия называется парной.
Если существует связь между одной
зависимой переменной у и
несколькими неизвестными
переменными х, говорят о
множественной регрессии, например,
y b0 b1 x1 b2 x2 bn xn
78.
2.2.1. МЕТОД НАИМЕНЬШИХ КВАДРАТОВЭтот метод наиболее часто используется для получения уравнения
регрессии. Предположим, между значениями х и у существует
линейная зависимость
y=b0+b1x.
Нам нужно найти такую функцию
у* = f(x)=b0* +b1* x
которая проходила бы как можно ближе к функции у.
Будем искать такую функцию f(x), для которой величина
n
S yi yi*
2
i 1
была бы минимальной.
Это метод наименьших квадратов.
79.
Итак, ищем минимум функцииn
S yi b b xi
i 1
*
0
*
1
2
Для этого нужно взять частные производные
функции S по а* и по b* ,
S S
* ; *
b0 b1
приравнять их к нулю и решить полученную
систему уравнений.
80.
Получим(1)
Имея уравнение у* = b0* + b1* x и подставляя в него
значения х за будущий период, можно осуществить
прогнозирование.
81.
Обозначим через ei разностьei yi yi* yi b *0 b1 * x
Случайная величина ei называется остатком регрессии в i-м
наблюдении.
Метод наименьших квадратов (МНК)можно
записать в виде:
n
S b0 , b1 e yi b0 b2 xi min
i 1
2
i
2
82.
ПримерИмеются данные о затратах на рекламу
(x, усл. ед.) и объеме реализации продукции (y, усл. ед.).
Таблица 1
xi
2
3
4
5
6
yi
1,4
1,7
1,8
1,7
1,9
Построить выборочное уравнение линейной парной
регрессии для выборки из табл. 1.
Определить прогноз объема продаж при затратах на
рекламу х = 7 у.е.
83.
Сведем вычисления в табл. 2Таблица 2
i
x
y
1
2
3
4
5
Сумма
2
3
4
5
6
20
1,4
1,7
1,8
1,7
1,9
8,5
xy
Таблица 1
xi
2
3
4
5
6
yi 1,4 1,7 1,8 1,7 1,9
x2
y*
ei
e2
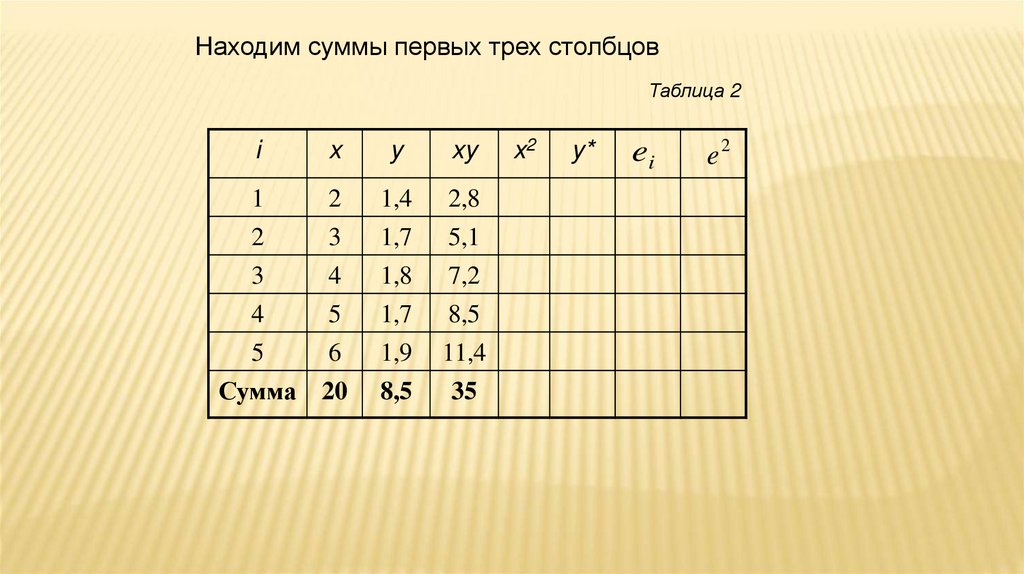
84.
Находим суммы первых трех столбцовТаблица 2
i
x
y
xy
1
2
2
3
1,4
1,7
2,8
5,1
3
4
1,8
7,2
4
5
5
6
1,7
1,9
8,5
11,4
Сумма 20
8,5
35
x2
y*
ei
e2
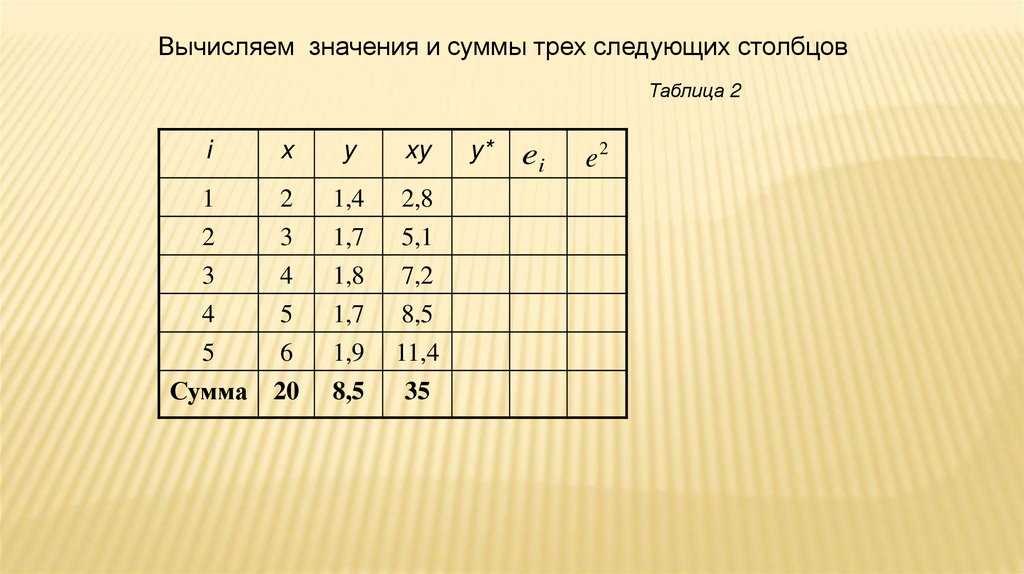
85.
Вычисляем значения и суммы трех следующих столбцовТаблица 2
i
x
y
xy
1
2
2
3
1,4
1,7
2,8
5,1
3
4
1,8
7,2
4
5
5
6
1,7
1,9
8,5
11,4
Сумма
20
8,5
35
y*
ei
e2
86.
b1n
n
n
1
1
1
Находим коэффициенты регрессии по системе (1)
n x i y i xi y i
n xi2 xi
1
1
n
n
2
5 35 20 8,5 175 170 5
0,1.
2
450 400 50
5 90 20
b0
n
n
1
1
yi b1 xi
n
i
x
y
xy
x2
1
2
2
3
1,4
1,7
2,8
5,1
4
9
3
4
5
4
5
6
1,8
1,7
1,9
7,2 16
8,5 25
11,4 36
Сумма 20
8,5
35
90
y*
ei
8,5 0,1 20 6,5
1,3.
5
5
e2
87.
Таким образом, уравнение регрессии имеет вид:y* b0 b1 x 1,3 0,1 x.
Величина коэффициента b1
показывает, что с увеличением
расходов на рекламу на 1 усл. ед.
объем продаж увеличится в среднем
на 0,1 усл. ед.
Пример 1. Имеются данные о затратах
на рекламу (x, усл. ед.) и объеме
реализации продукции (y, усл. ед.).
(2)
88.
ГРАФИК РЕГРЕССИИ89.
По уравнению регрессии (2) находим приближенные(теоретические) значения y*:
y * ( x 2) 1.3 0.1 2 1.5
y * ( x 3) 1.3 0.1 3 1.6
y * ( x 4) 1.3 0.1 4 1.7
y * ( x 5) 1.3 0.1 5 1.8
y * ( x 6) 1.3 0.1 6 1.9
Таблица 2
i
x
y
xy
x2
1
2
1,4
2,8
4
2
3
1,7
5,1
9
1,6
3
4
1,8
7,2
16
1,7
4
5
1,7
8,5
25
1,8
5
6
1,9
11,4
36
1,9
Сумма
20
8,5
35
90
y*
ei
1,5
y* b0 b1 x 1,3 0,1 x. (2)
e2
90.
Вычисляем остатки регрессии:e1 y1 y *1 1.4 1.5 0.1
e2 y2 y *2 1.7 1.6 0.1
e4 y4 y *4 1.7 1.8 0.1
e3 y3 y *3 1.8 1.7 0.1
e5 y5 y *5 1.9 1.9 0
Таблица 2
i
x
y
xy
x2
y*
ei
e2
1
2
2
3
1,4
1,7
2,8
5,1
4
9
1,5
1,6
-0,1
0,1
0,01
0,01
3
4
4
5
1,8
1,7
7,2
8,5
16
25
1,7
1,8
0,1
-0,1
0,01
0,01
5
Сумма
6
20
1,9
8,5
11,4
35
36
90
1,9
0
0
0,04
91.
Рассчитаем объем продажпри х = 7
y* b0 b1 x 1,3 0,1 x.
у* = 1,3+0,1х =1,3 +0,1*7 = 2 (у.е).
92.
САМОСТОЯТЕЛЬНАЯ РАБОТАЗадание.
При установлении взаимосвязи
между уровнем инфляции (х) и ценой на
некоторый товар (y) получено уравнение
регрессии
y* = 3х -4
Осуществите прогнозирование
цены на товар при значении инфляции 10.
А. 26.
В. 30
С. 40
D. 37.
93.
САМОСТОЯТЕЛЬНАЯ РАБОТАЗадание.
При обработке статистических
данных получены коэффициенты
линейной регрессии:
b0* = 3,5; b1* = -0,8.
Осуществите прогноз
исследуемого процесса для Х= 20.
94.
Регрессионный анализ в Excel осуществляется:- в Пакете анализа,
- графически,
- а также функциями:
ЛИНЕЙН, ТЕНДЕНЦИЯ,
ЛГРФПРИБЛ, РОСТ,
ПРЕДСКАЗ, ОТРЕЗОК,
НАКЛОН, СТОШУХ и другими.
95.
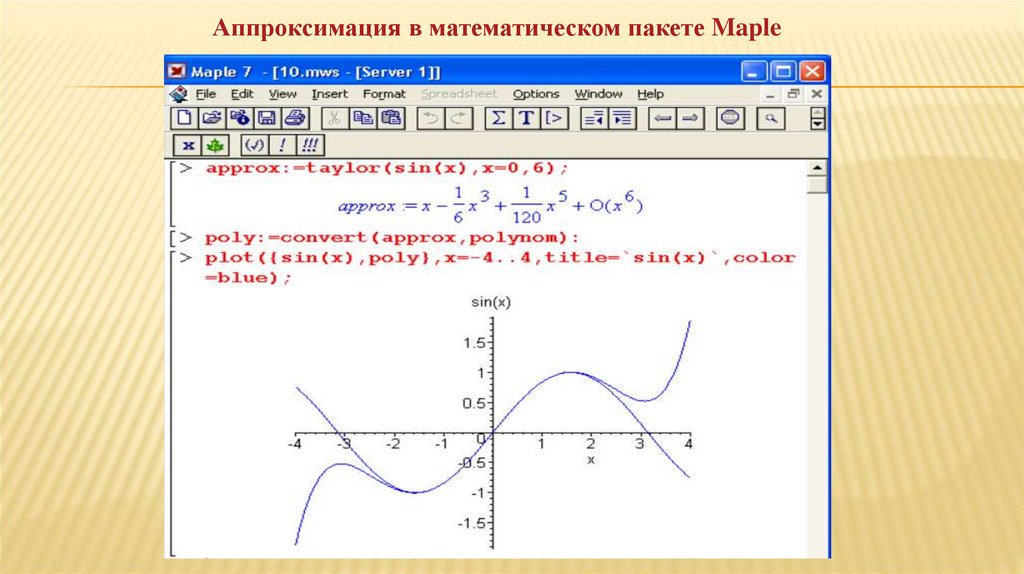
Аппроксимация в математическом пакете Maple96.
ИНДИВИДУАЛЬНАЯ РАБОТАОпределите уравнение регрессии
и осуществите прогнозирование
согласно индивидуального задания 1
Контрольной работы
97.
2.2.3. НЕЛИНЕЙНАЯ РЕГРЕССИЯНелинейные регрессии делятся на два класса:
• регрессии, нелинейные относительно включенных в анализ
объясняющих переменных, но линейные по оцениваемым
параметрам,
• регрессии, нелинейные по оцениваемым параметрам.
Регрессии, нелинейные по объясняющим переменным:
• полиномы разных степеней у = а + b1• х + b2• х2 + b3• х3 + ;
• равносторонняя гипербола
b
у=а+
x
+ ;
98.
НЕЛИНЕЙНАЯ РЕГРЕССИЯРегрессии, нелинейные по оцениваемым параметрам:
• степенная у = а • хb• ;
• показательная у = а • bх • ;
• экспоненциальная у = еa+bx .
Построение уравнения регрессии сводится к оценке
ее параметров.
Для оценки параметров регрессий, линейных по
параметрам, используют метод наименьших квадратов
(МНК)
99.
2.2.4. МНОЖЕСТВЕННАЯ РЕГРЕССИЯМножественная регрессия - уравнение связи переменной у
с несколькими независимыми переменными:
y=f(x1,x2,...,хp),
где
у - зависимая переменная (результативный признак);
x1, x2, ..., хp - независимые переменные (факторы).
Для оценки параметров уравнения
множественной регрессии применяют
метод наименьших квадратов (МНК).
100.
МНОЖЕСТВЕННАЯ РЕГРЕССИЯДля построения уравнения множественной
регрессии чаще используются следующие функции:
• линейная - у = а +b1•x1+b2 –х2 +…+bp•xр+ ;
• степенная -y a x1b1 xb22 ... xbpp ε;
• экспонента -y
a b1 x1 b2 x2 ... bp x p
e
1
;
y • гипербола a b1 x1 b2 x 2 ... b p x p ε




































































 Математика
Математика Информатика
Информатика








