Квадратні рівняння. Розв’язування неповних квадратних рівнянь

1.

Математика – це
пізнавально,
корисно і, зрештою,
просто цікаво...
Герберт Уельс

2. Квадратні рівняння. Розв’язування неповних квадратних рівнянь

3. 1. Рівняння – це ...

а) вираз, що містить невідомі числа;
б) вираз, що містить невідомі букви;
в) рівність, що містить невідомі
числа, позначені буквами;
г) рівність, що містить невідомі
числа.

4. 2. Виберіть серед наведених неправильне твердження:

а) у будь-якій частині рівняння можна звести
подібні доданки або розкрити дужки, якщо вони
є;
б) обидві частини рівняння можна помножити
або поділити на одне й те саме число, відмінне
від нуля;
в) будь-який член рівняння можна перенести з
однієї частини рівняння в іншу, змінивши його
знак на протилежний;
г) обидві частини рівняння можна помножити
або поділити на одне й те саме число.

5. 3. Два рівняння називають рівносильними, якщо...

а) кожне з них не має коренів;
б) кожне з них має корінь, що
дорівнює нулю;
в) кожне з них має ті ж самі корені;
г) кожне з них має ті ж самі корені
або обидва не мають розв’язків.

6. 4. Розв’язати рівняння означає...

а) знайти його корені;
б) звести рівняння до вигляду ax=b;
в) знайти його корені або показати,
що їх немає;
г) розкрити дужки, звести подібні
доданки.

7. 5. Лінійне рівняння – це рівняння виду...

8. 6. Рівняння першого степеня називають рівняння виду ax = b, якщо...

а) a = 0;
б) b = 0;
в) а ≠ 0;
г) x = 0.

9. Для чого вивчати квадратні рівняння?

У математиці, фізиці,
економіці,практичній діяльності
людини трапляються задачі, що
приводять до рівнянь, в які
змінна входить у другому
степені.

10. Наприклад

• Задача. Площа прямокутної ділянки
дорівнює 600м². Довжина ділянки на 10
м більша від ширини. Знайти ширину
ділянки.

11. Квадратні рівняння

Квадратним рівнянням називають
рівняння виду ах² +bх + с = 0, де х
– змінна, а, b, с – деякі числа,
причому а≠0.
Числа а, b, с називають коефіцієнтами
квадратного рівняння:
а – перший коефіцієнт;
b – другий коефіцієнт;
с – вільний член.

12. Зведені квадратні рівняння

Квадратне рівняння, перший
коефіцієнт якого дорівнює 1,
називають зведеним.
Наприклад.
х² + 5х – 37 = 0 – є зведеним;
5х² - 2х – 4 = 0 - не є зведеним.

13. Неповні квадратні рівняння

Якщо в квадратному рівнянні
ах² + bх + с = 0 хоча б один з
коефіцієнтів b або с дорівнює
нулю, то таке рівняння
називають неповним
квадратним рівнянням.
Наприклад. -8х² = 0; 5х² - 3 = 0;
4х² + 5х = 0; х² - 7х = 0.

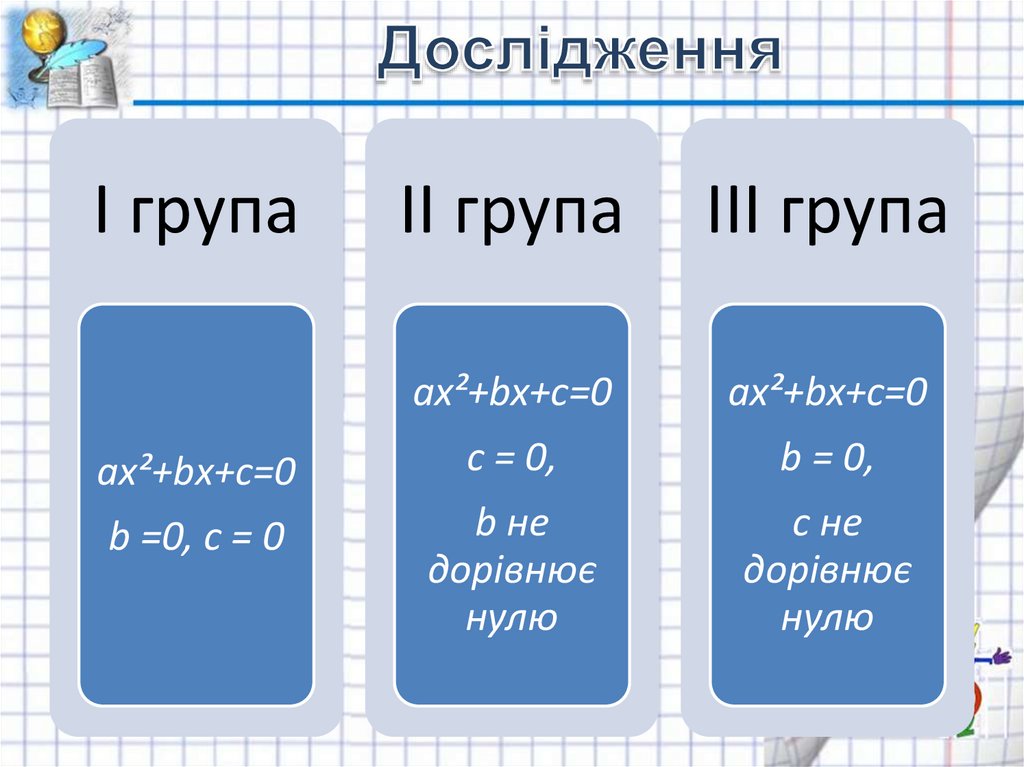
14. Дослідження

І група
ІІ група
ІІІ група
ах²+bх+с=0
ах²+bх+с=0
ах²+bх+с=0
с = 0,
b = 0,
b =0, с = 0
b не
дорівнює
нулю
c не
дорівнює
нулю

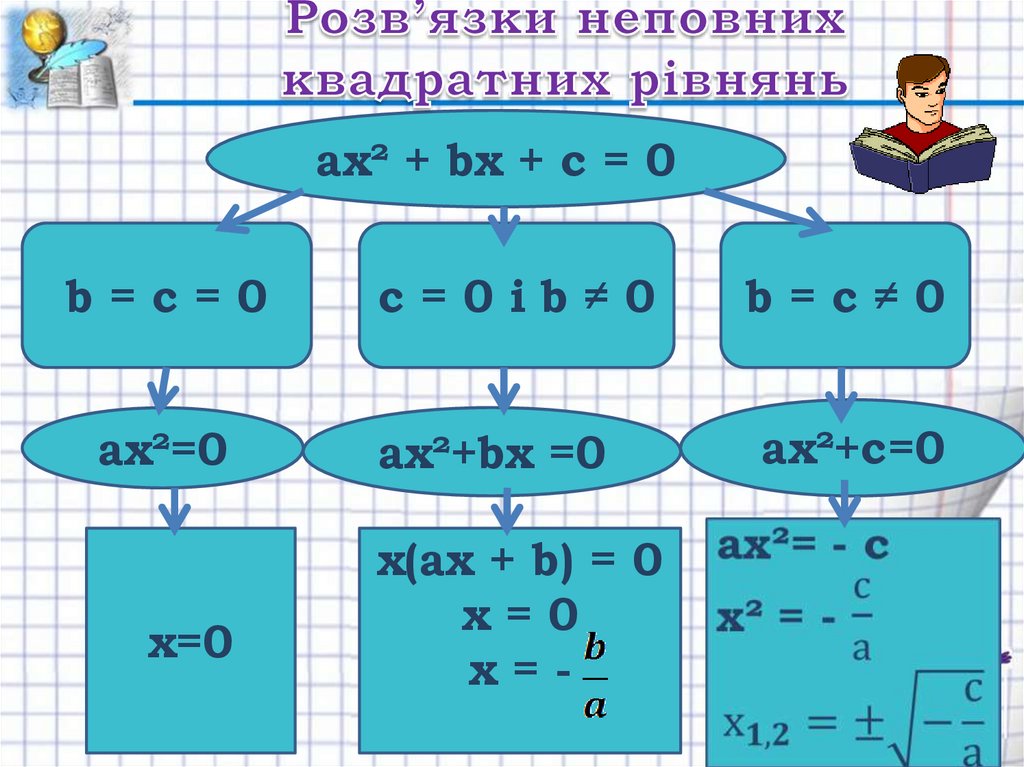
15. Розв’язки неповних квадратних рівнянь

ах² + bх + с = 0
b=с=0
с=0іb≠0
b=с≠0
ах²=0
ах²+bx =0
ах²+c=0
х=0
x(ax + b) = 0
х=0
х=-

16.

Як ви
думаєте?
Які з рівнянь є
квадратними?
1) х² - 2х + 3 = 0;
2) х² - 3х³ = 0;
3) х² + 1/х² = 5;
4) 7х – х² = 0;
5) 4х – 5= 2х + 7;
6) 1 – 5х² = 0.
Відповідь: 1), 4), 6).

17.

Запишіть коефіцієнти
а, b і c кожного
квадратного рівняння:
1) 2х² + 3х – 5 = 0;
2) 3х² + 9 = 0;
3) 3х - х² + 7 = 0;
4) 5х² = 0;
5) 8х - х² =0;
6) 2 + 4х - х² = 0.

18. Відповідь:

1) а = 2, b = 3, с = -5;
2) а = 3, b = 0, с = 9;
3) а = -1, b = 3, с = 7;
4) а = 5, b = 0, с = 0;
5) а = -1, b = 8, с = 0;
6) а = -1, b = 4, с = 2;

19.

Складіть квадратне
рівняння, коефіцієнти
якого дорівнюють:
a) а = -1; b = 4; с = 0;
b) а = -6; b = 0; с = 0;
c) а = 8; b = 0; с = 23;

20. Відповідь:

a) -х² + 4х = 0;
b) -6х² = 0;
c) 8х² + 23 = 0;

21. Фізкультхвилинка

Трава - низенька-низенька, (присісти)
Дерева - високі-високі (потягнутися)
Вітер дерева колише, гойдає, (нахили
тулуба)
То вправо, то вліво хитає,
То вперед, то назад, то вниз пригинає.
Птахи летять, відлітають, (помахати
руками, як крилами)
А учні тихенько за парти сідають
І геометрію далі вивчають.

22. Розв’язки неповних квадратних рівнянь

ах² + bх + с = 0
b=с=0
с=0іb≠0
b=с≠0
ах²=0
ах²+bx =0
ах²+c=0
х=0
x(ax + b) = 0
х=0
х=-

23. Самостійна робота

І група
ІІ група
ІІІ група
•(3х – 1)(х + 4) = − 4;
2
•2(х − 2) = (х − 3)(х + 3);

24. Домашнє завдання

• Опрацювати п.18.
• Виконати вправи №593, 595, 597 і 602.
• Вправа № 604(1) - додатково

25. Підсумок уроку

Д – досвід (Що робили? Що пам’ятаєте?)
Р – рефлексія (Які відчуття, реакція?)
І – інформація (Яку інформацію
одержали, які висновки зробили?)
Д – дії (Як ви будете діяти в
майбутньому?)