Похожие презентации:
Элементы теории поля
1.
Математика 2Элементы теории поля
Лектор:
доцент отделения математики и информатики
Имас Ольга Николаевна
2.
Связь между интегралами двух типовd xdy ds xoy cos ds
d xdz ds xoz cos ds
Тогда
d ydz ds yoz cos ds
Pdydz Qdxdz Rdxdy P cos Q cos R cos ds
S
S
где cos , cos , cos – направляющие косинусы вектора нормали к
поверхности
N {cos ;cos ;cos }
3.
Пусть задано векторное полеF Pi Q j Rk
N {cos ;cos ;cos }
N
Тогда
F , N ds P cos Q cos R cos ds
F
dS
Механически
Тогда
F , N ds F cos F , N ds
- объем цилиндра площадью dS и высотой F cos(F,N)
ОПР 6
поверхностный интеграл II типа выражает поток векторного поля F через
поверхность S
П F , N ds Pdydz Qdxdz Rdxdy
пропустить 10 клеточек
S
S
4.
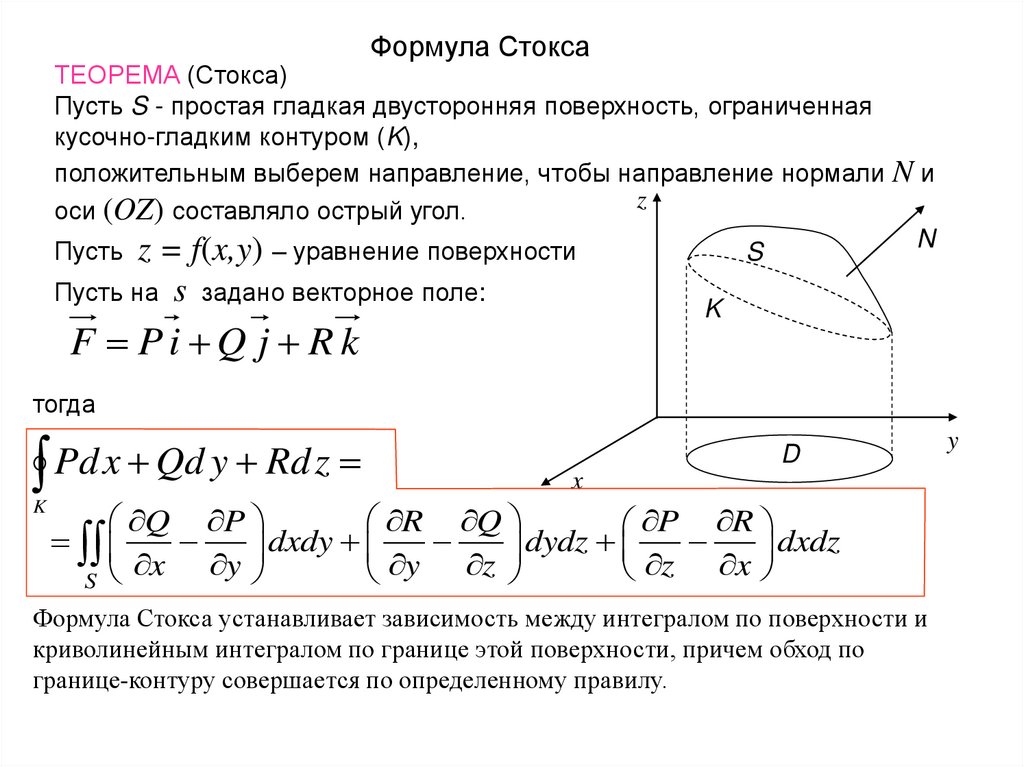
Формула СтоксаТЕОРЕМА (Стокса)
Пусть S - простая гладкая двусторонняя поверхность, ограниченная
кусочно-гладким контуром (K),
положительным выберем направление, чтобы направление нормали N и
z
оси (OZ) составляло острый угол.
N
Пусть z = f(x,y) – уравнение поверхности
S
Пусть на s задано векторное поле:
K
F Pi Q j Rk
тогда
Pd x Qd y Rd z
K
D
x
Q P
R Q
P R
dxdy
dydz
dxdz
x y
z x
y z
S
Формула Стокса устанавливает зависимость между интегралом по поверхности и
криволинейным интегралом по границе этой поверхности, причем обход по
границе-контуру совершается по определенному правилу.
y
5.
ОПР 7Вектор B, определяемый проекциями
R Q
P R
Q P
Bx
By
Bz
y z
z x
x y
называется вихрем или ротором векторной функции F P i Q j R k
и обозначается
i j k
rot F
x y z
P Q R
Тогда формулу Стокса можно записать:
Циркуляция вектора вдоль контура некоторой поверхности
равна потоку вихря через эту поверхность
F d s n, rotF ds
K
s
6.
Замечание 1. Если S параллельна одной из координатных плоскостей,мы получим формулу Грина, как частный случай формулы Стокса
Замечание 2. В случае выполнения условия полного дифференциала
P'y= Q'x
вихрь равен нулю.
пропустить 20 клеточек
P'z= R'x
Q'z= R'y
7.
(вспомним)Формула Остроградского - Гаусса
s2
ТЕОРЕМА
Пусть тело V ограничено кусочно-гладкими поверхностями,
в области V определены функции
s3
P(x,y,z), Q(x,y,z), R(x,y,z)
вместе со своими частными производными.
Тогда
s1
P Q R
x y z dxdydz Pdydz Qdxdz Rdxdy
V
S
пропустить 10 клеточек
Таким образом формулы Грина, Стокса и Остроградского-Гаусса выражают
интеграл, распространенный на некоторый геометрический образ через
интеграл, взятый по границе этого образа.
Грина – по двумерному пространству
Стокса – по двумерному криволинейному пространству
Остроградского-Гаусса – по трехмерному пространству
V
8.
ОПР 8Выражение
P Q R
x y z
называется дивергенцией вектора
F Pi Q j Rk
(расходимость вектора)
P Q R
div F
x y z
– скаляр
Тогда формула Остроградского – Гаусса может быть записана:
div F dv F , N ds
V
пропустить 30 клеточек
S
9.
Специальные поляОПР 9. Векторное поле F называется потенциальным, если существует
скалярная величина U, для которой F служит градиентом U.
grad U F
Условие потенциальности поля.
Для того, чтобы поле F было потенциальным, необходимо и достаточно, чтобы
во всей рассматриваемой области выполнялись равенства:
Fz Fy
y
z
то есть чтобы
Fx Fz
z
x
Fy Fx
x
y
rot F 0
Т.о. потенциальное поле является безвихривым
пропустить 10 клеточек
10.
ОПР 10. Векторное поле F называется соленоидальным (трубчатым), еслисуществует векторная величина B, для которой F служит вихрем.
F rot B
то есть чтобы
Bz By
Fx
y
z
Bx Bz
Fy
z
x
By Bx
Fz
x
y
ТЕОРЕМА Условие соленоидальности поля.
Для того, чтобы поле F было соленоидальным, необходимо и достаточно,
чтобы во всей рассматриваемой области выполнялось равенство:
divF 0
Если
rot F 0
и
divF 0
то поле F называется полем общего вида.
ТЕОРЕМА .
Любое поле можно представить в виде суммы потенциального и
соленоидального полей.
11.
ОПР 11. Скалярное поле U называется гармоническим, если оно удовлетворяетуравнению Лапласа.
2
2
2
U
U
U
2U U 2 2 2 0
x y z
Операторы и ∆ называются
i
j k
x
y
z
2
2
2
2 2 2
x y z
- оператор Гамильтона
- оператор Лапласа
ТЕОРЕМА Условие гармонического поля.
Для того, чтобы поле U было гармоническим, необходимо и достаточно,
чтобы оно было потенциальным и соленоидальным одновременно,
т.е. если F grad U , то
rot F 0
divF 0










 Математика
Математика








