Похожие презентации:
Матрицы. Логическая структура стека
1. МАТРИЦЫ
2.
Пусть задан произвольный n-мерный массивB i1 : k1 , i2 : k2 , ..., in : kn
Адрес произвольного элемента:
B j1 , j2 , ..., jn
ADDR B j1, j2 , ..., jn ADDR B i1, i2 , ..., in
n
n
m 1
m 1
l * im Dm l * jm Dm
3. Величина Dm:
при отображении строками :Dm km 1 im 1 1 * Dm 1 ,
m n 1,...,1 Dn 1,
при отображении столбцами :
Dm km 1 im 1 1 * Dm 1 ,
m 2,..., n D1 1.
4. Пример
АMATR
ADDR(MATR(2,4,1))
ADDR(MATR(2,4,1))-102
3
2
4
1
3
6
5
l * i1D1 i2 D2 i3 D3
l1D1 , l2 D2 и i3 D3
30
10
2
INTEG
MATR(2:3,4:6,1:5)
2
5.
MATR(2:3,4:6,1:5)Dm km 1 im 1 1 * Dm 1 , m n 1,...,1 Dn 1
D3=1
D2=(5-1+1)*1=5
D1=(6-4+1)*5=15
l * i1D1 i2 D2 i3 D3 102.
2*(2*15+4*5+1*1)
6.
Пусть начальный адрес массива MATR=1000.Тогда его элемент с индексами 2, 5, 4 будет
располагаться по адресу :
ADDR(MATR(2,5,4))=ADDR(MATR(2,4,1))-
102+30*2+10*5+2*4=1000-102+118=1016.
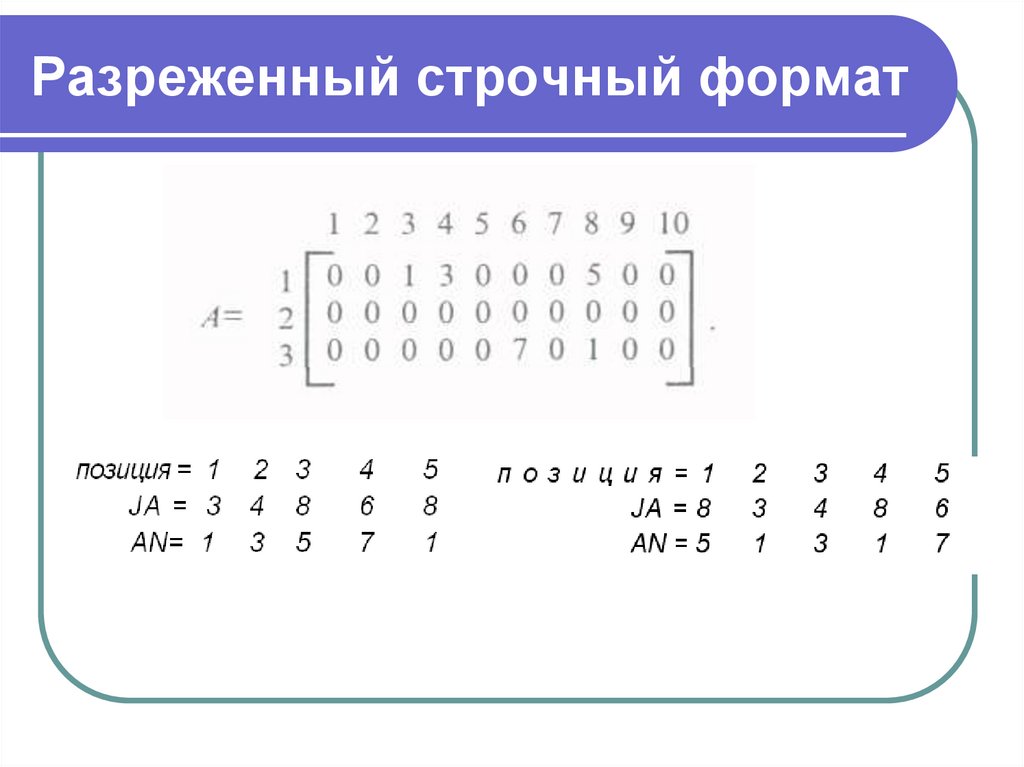
7. Разреженный строчный формат
8. Сложение разреженных векторов с использованием расширенного вещественного накопителя
9. Сложение разреженных векторов с использованием расширенного вещественного накопителя
10. Сложение разреженных векторов с использованием расширенного целого массива указателей
Скалярное умножение двух разреженных векторовс использованием массива указателей
11. Диагональная схема хранения ленточных матриц
Здесь - полуширина, а 2 +1 – ширина ленты.Лентой матрицы А называется множество
элементов, для которых i-j .
Верхняя полулента состоит из элементов,
находящихся в верхней части ленты, т.е. таких, что
0<i-j ;
Массив имеет размеры n*( +1).
12. Диагональная схема хранения ленточных матриц
12
3
А
4
5
6
7
1 2 3 4
1 0 0 0
0 2 8 9
0 8 3 0
0 9 0 4
0 0 0 10
0 0 0 0
0 0 0 0
5 6 7
0 0 0
0 0 0
0 0 0
10 0 0 ;
5 11 12
11 6 0
12 0 7
0 0 1
0 0 2
0 8 3
AN I , J 9 0 4
0 10 5
0 11 6
12 0 7
13. Профильная схема хранения симметричных матриц
Для каждой строки iсимметричной
матрицы А
положим
i i jmin i
Схема Дженнингса
1
2
3
А
4
5
6
7
1 2 3 4
1 0 0 0
0 2 8 9
0 8 3 0
0 9 0 4
0 0 0 10
0 0 0 0
0 0 0 0
5 6 7
0 0 0
0 0 0
0 0 0
10 0 0
5 11 12
11 6 0
12 0 7
14. Профильная схема хранения симметричных матриц
Оболочка матрицы А – это множество элементов, для которых
a ij
0 i j i
В строке i оболочке принадлежат все элементы со
столбцовыми индексами от j min i до i-1, всего i
элементов.
Диагональные элементы не входят в оболочку.
Профиль матрицы А определяется как число
элементов в оболочке:
profile A i
i
15. Профильная схема хранения симметричных матриц
ПозицияAN
IA
= 1 2 3 4 5 6 7 8 9 10 11 12 13 14
= 1 2 8 3 9 0 4 10 5 11 6 12 0 7
= 1 2 4 7 9 11 14
1
2
3
А
4
5
6
7
1 2 3 4
1 0 0 0
0 2 8 9
0 8 3 0
0 9 0 4
0 0 0 10
0 0 0 0
0 0 0 0
5 6 7
0 0 0
0 0 0
0 0 0
10 0 0
5 11 12
11 6 0
12 0 7
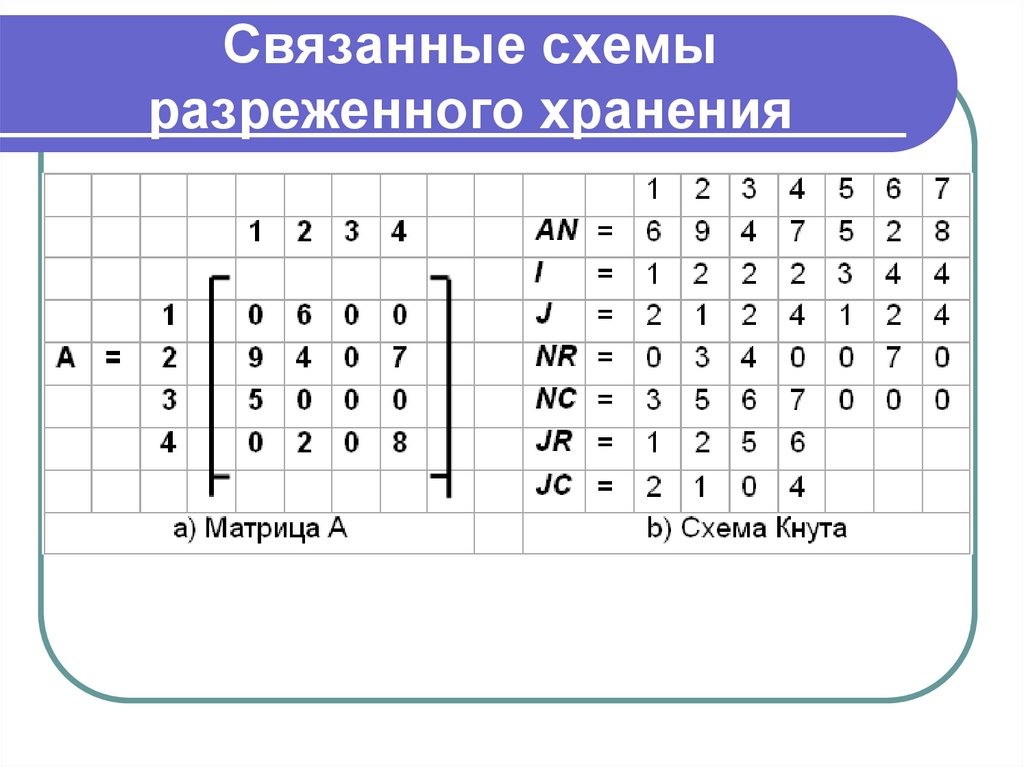
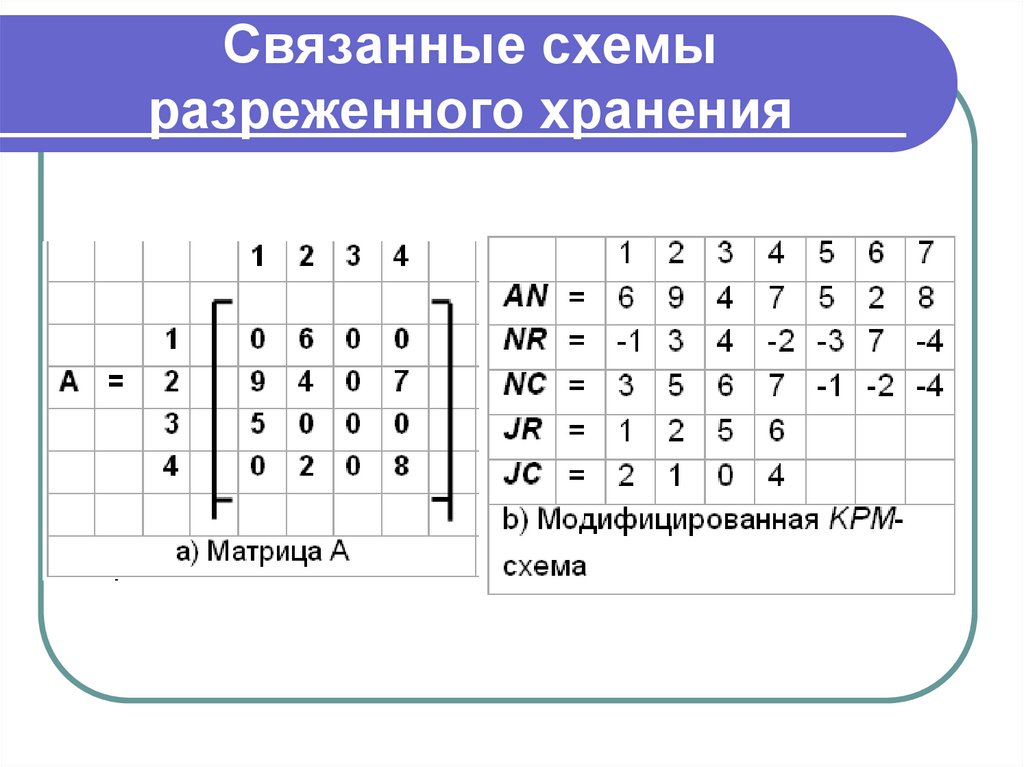
16. Связанные схемы разреженного хранения
17. Связанные схемы разреженного хранения
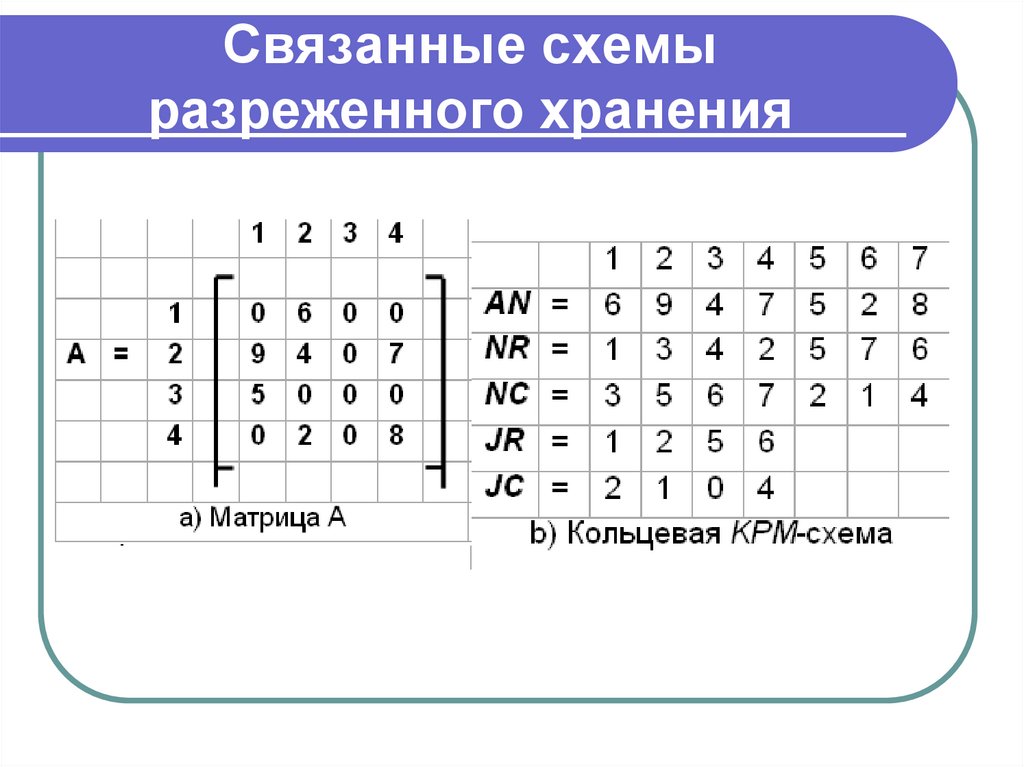
18. Связанные схемы разреженного хранения
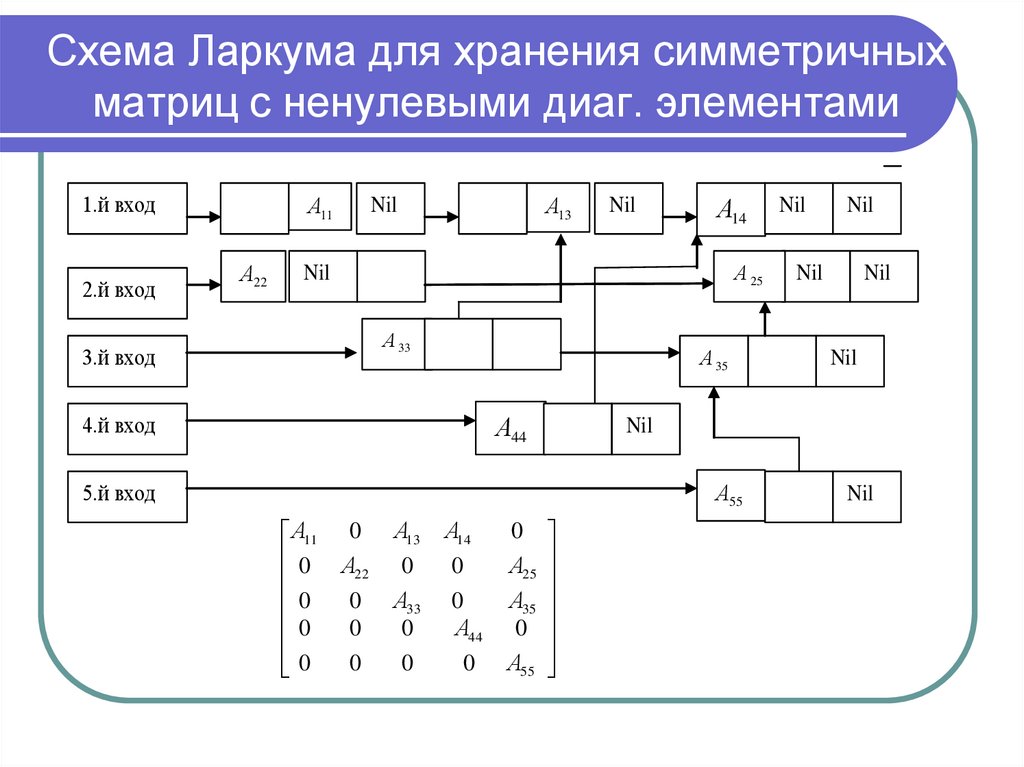
19. Схема Ларкума для хранения симметричных матриц с ненулевыми диаг. элементами
А110
0
0
0
0
А22
0
0
0
А13
0
А33
0
0
А14
0
0
А44
0
0
А25
А35
0
А55
20. Схема Ларкума для хранения симметричных матриц с ненулевыми диаг. элементами
1.й вход2.й вход
А11
А22
А13
Nil
Nil
А14
А 25
Nil
А 33
3.й вход
А 35
А44
4.й вход
5.й вход
0
А22
0
0
0
А13
0
А33
0
0
А14
0
0
А44
0
0
А25
А35
0
А55
Nil
Nil
Nil
Nil
Nil
А55
А11
0
0
0
0
Nil
Nil
21. ДАННЫЕ ДИНАМИЧЕСКОЙ СТРУКТУРЫ
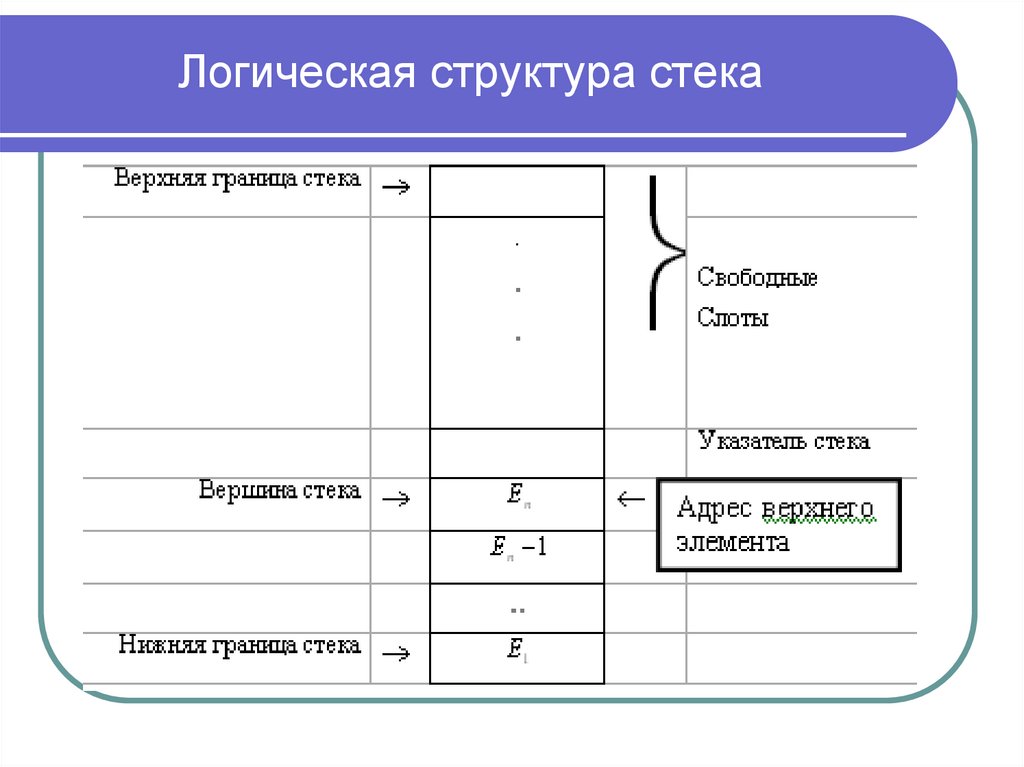
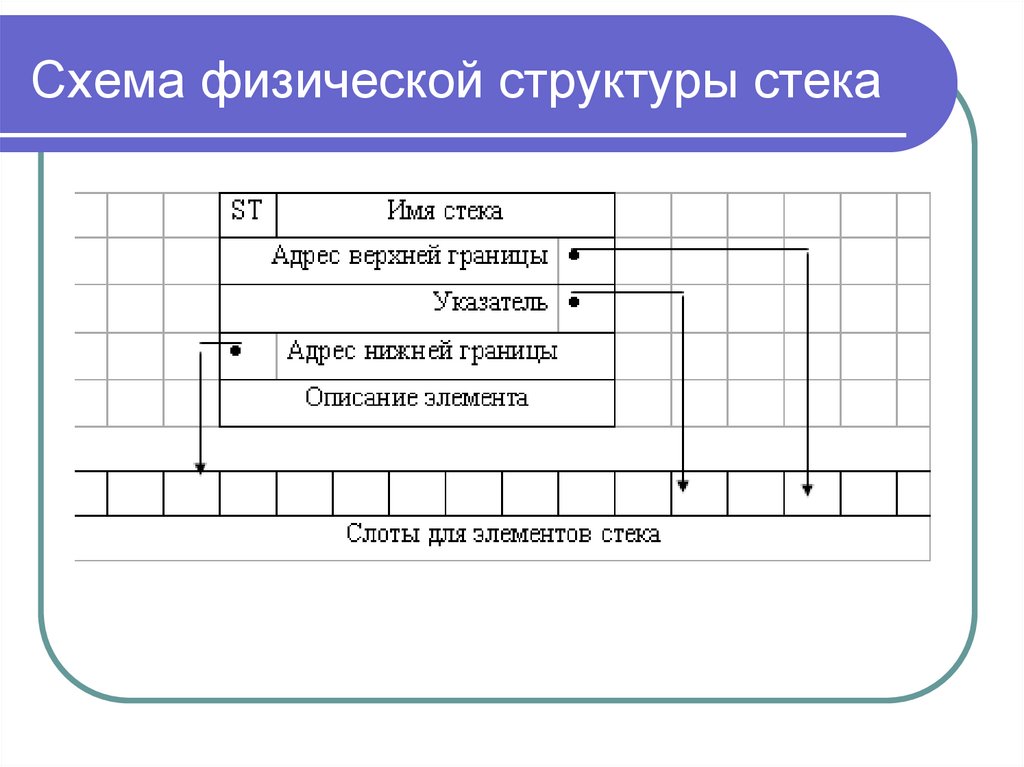
Списком называется линейно-упорядоченнаяпоследовательность элементов данных Е(1),
Е(2),..., Е(n)
последовательный список - последовательное
расположение элементов списка
динамически связанный список упорядоченность элементов задается с помощью
специальных указателей
Стек (список LIFO — Last In First Out)















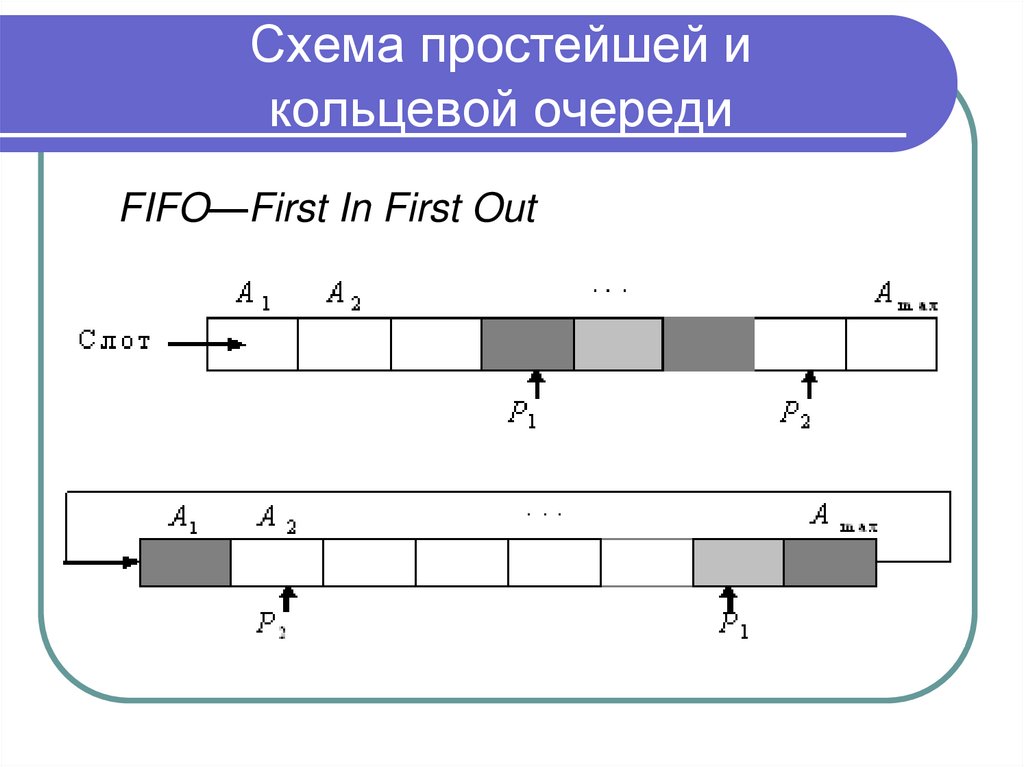
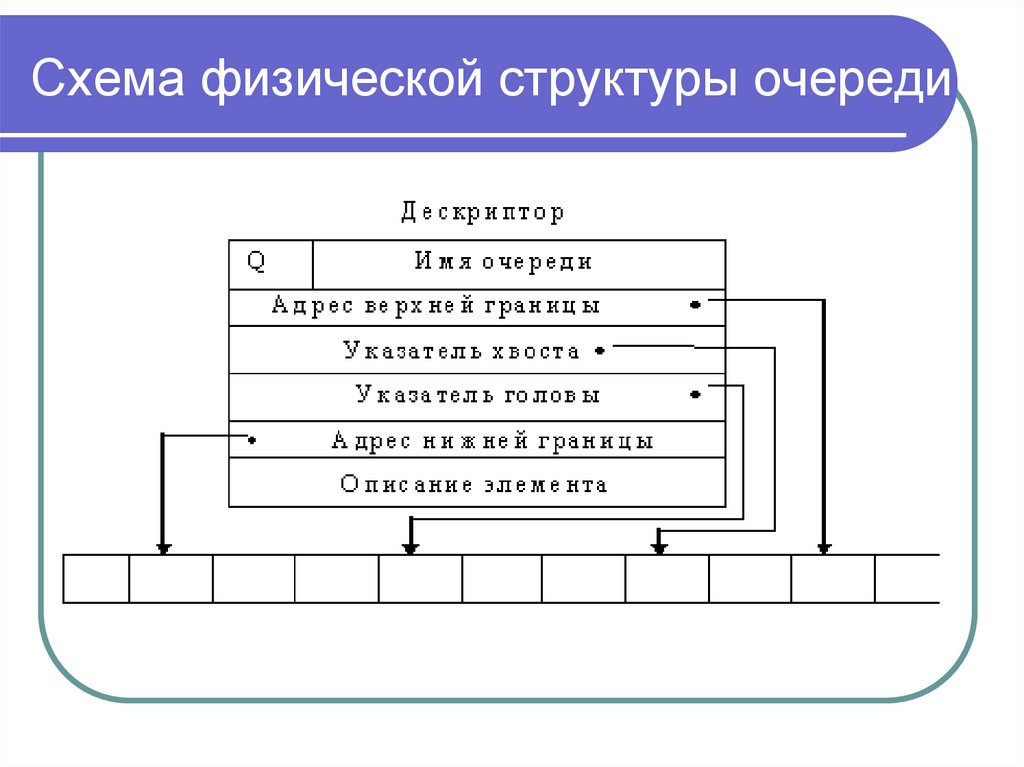
 Программирование
Программирование








