Похожие презентации:
Дискретная случайная величина
1.
Дискретная случайнаявеличина
Арбузова Елизавета
ТЛБО-01-21
2.
• Определение 1. Случайной величиной называется переменнаявеличина, которая в зависимости от исхода испытания случайно
принимает одно из множества возможных значений.
• Определение 2. Случайная величина, принимающая различные
значения, которые можно записать в виде последовательности,
называется дискретной случайной величиной.
• Определение 3. Две случайные величины называются
независимыми, если закон распределения одной из них не
меняется от того, какие возможные значения приняла другая
величина. В противном случае случайные величины называются
зависимыми.
3.
Числовые характеристикидискретной случайной величины
1. Математическое ожидание
• Математическим ожиданием дискретной случайной вел
ичины называется сумма произведений значений этой случ
айной величины на соответствующие вероятности:
• Математическое ожидание –
это среднее значение данной случайной величины, центр
ее распределения. Из определения следует, что M(X) −
величина неслучайная, постоянная.
4.
Задача*Случайная величина Х задана законом распределения.
Найти математическое ожидание.
Х
1
2
3
P
0,3
0,5
0,2
5.
Решение*Вычислим ее математическое
ожидание:
M(X) = 1∙0,3+2∙0,5+3∙0,2=0,3+1+0,6=1,9.
Ответ: M(X)=1,9.
6.
2. ДисперсияОпределение 1. Разность называется отклонением случайной величины Х от ее
математического ожидания.
Теорема. Математическое ожидание отклонения случайной величины от ее
математического ожидания равно нулю.
Определение 2. Дисперсией случайной величины называется математическое
ожидание квадрата отклонения этой случайной величины от ее
математического ожидания:
Если случайная величина Х − дискретная, то
Средним квадратическим отклонением случайной величины называется
квадратный корень из дисперсии:
7.
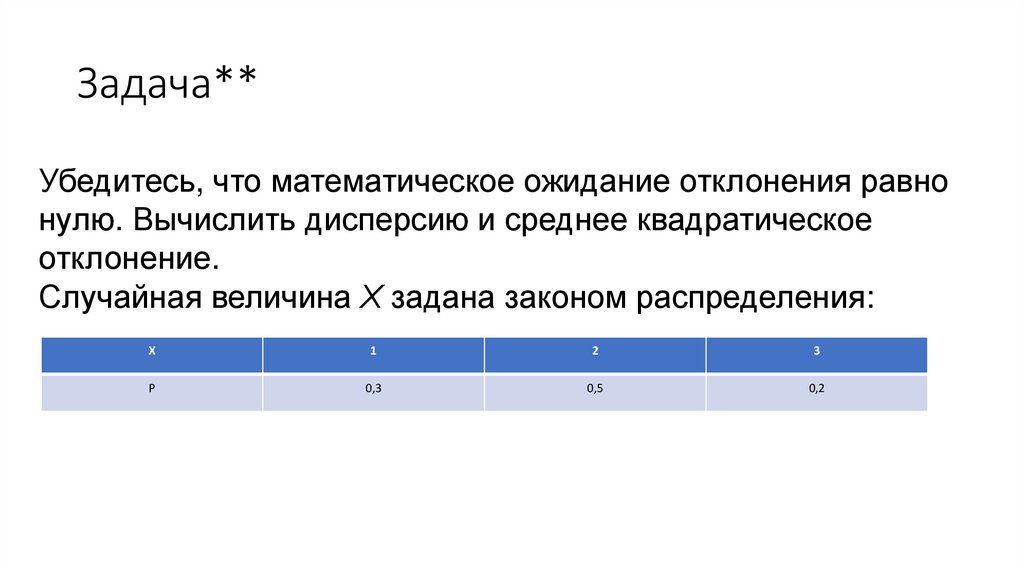
Задача**Убедитесь, что математическое ожидание отклонения равно
нулю. Вычислить дисперсию и среднее квадратическое
отклонение.
Случайная величина Х задана законом распределения:
Х
1
2
3
P
0,3
0,5
0,2
8.
Решение**Вычислим ее математическое ожидание:
• M(X) = 1∙0,3+2∙0,5+3∙0,2=0,3+1+0,6=1,9.
Для этого составим закон распределения случайной величины Х−M(Х): из всех
значений Х вычтем M(X)=1,9.
Х−M(Х)
−0,9
0,1
1,1
P
0,3
0,5
0,2
M(X-M(X))=−0,9∙0,3+0,1∙0,5+1,1∙0,2=−0,27+0,05+0,22=−0,27+0,27=0.
Вычислим дисперсию и среднее квадратическое отклонение:
D(X)=(−0,9)2∙0,3+(0,1)2∙0,5+(1,1)2∙0,2=0,243+0,005+0,242=0,49;
Ответ: M(X-M(X))=0 , D(X)=0,49 ,
9.
• Формула для вычисления дисперсии. Дисперсия случайнойвеличины равна разности между математическим ожиданием
квадрата этой величины и квадратом ее математического
ожидания.
10.
ПримерНайдем дисперсию случайной величины Х.
Случайная величина Х задана законом распределения:
Х
1
2
3
P
0,3
0,5
0,2
Вычислим ее математическое ожидание
M(X) = 1∙0,3+2∙0,5+3∙0,2=0,3+1+0,6=1,9.
M(X2) = 12∙0,3+22∙0,5+32∙0,2 = 1∙0,3+4∙0,5+9∙0,2 = 4,1.
D(X) = M(X2) − M2(X) = 4,1−1,92 = 4,1−3,61= 0,49.
Ответ: D(X) =0,49.
11.
Задача***Закон распределения дискретной случайной величины X имеет вид:
xi
-2
-1
0
1
2
pi
0,2
0,1
0,2
p4
p5
Найти вероятности p4 , p5 и дисперсию D(X) , если математическое
ожидание M(X)= 0,1
12.
Решение***• Случайная величина X может принимать только пять значений, соответствующие события образуют
полную группу, поэтому:
p1+p2+p3+p4+p5=1
0,2+0,1+0,2+p4+p5=1
p4+p5=0,5
• По определению математического ожидания:
M(X)=x1p1+x2p2+x3p3+x4p4+x5p5
0,1=-2*0,2-1*0,1+0*0,2+p4+2*p5
р4+2*р5=0,6
• Вероятности p4 и p5 найдем из решения системы:
p4+p5=0,5
p4+2*p5=0,6 => p5=0,1, p4=0,4
13.
Для нахождения дисперсии заполнимвспомогательную расчетную таблицу:
xi
-2
-1
0
1
2
Суммы:
pi
0,2
0,1
0,2
0,4
0,1
1
4
1
0
1
4
0,8
0,1
0
0,4
0,4
2
xi
pi*xi
2
D(X)=M(X2)-(M(X))2 = Σ xI2 *pI -(0,1)2=1,7-0,01=1,69
Ответ: р4 =0,4 , p5=0,1 , D(X)=1,69.
1,7












 Математика
Математика








