Математические основы нейронных сетей

1.

Сибирский государственный индустриальный университет
Интеллектуальные
системы и технологии
Бабичева Н.Б.
Новокузнецк

2.

Список литературы
1 Станкевич, Л. А. Интеллектуальные системы и технологии : учебник и практикум. – Москва
: Издательство Юрайт, 2019. – 397 с. – ISBN 978-5-534-02126-4. – URL: https://www.biblioonline.ru/bcode/433370 (дата обращения: 17.03.2020);
2 Доррер, Г. А. Методы и системы принятия решений : учебное пособие. – Красноярск : СФУ,
2016.
–
210
с.
–
ISBN
978-5-7638-3489-5.
–
URL:
http://biblioclub.ru/index.php?page=book&id=497093 (дата обращения: 17.03.2020);
3 Галушкин, А.И. Нейронные сети: основы теории : учебное пособие. – Москва : Горячая
линия - Телеком, 2012. – 496 c. – ISBN 978-5-9912-0082-0. – URL:
http://www.studentlibrary.ru/book/ISBN9785991200820.html (дата обращения: 17.03.2020);
4 Ясницкий, Л.Н. Интеллектуальные системы : учебник. – Москва : Лаборатория знаний,
2016.
–
224
c.
–
ISBN
978-5-00101-417-1.
–
URL:
http://www.studentlibrary.ru/book/ISBN9785001014171.html (дата обращения: 17.03.2020);
5 Рашка, С. Python и машинное обучение: крайне необходимое пособие по новейшей
предсказательной аналитике, обязательное для более глубокого понимания методологии
машинного обучения : практическое пособие. – Москва : ДМК-пресс, 2017. – 418 c. – ISBN
978-5-97060-409-0. – URL: http://www.studentlibrary.ru/book/ISBN9785970604090.html (дата
обращения: 17.03.2020).

3.

Раздел 2.Основы нейронных сетей
2.1 Математические основы нейронных сетей

4.

Математические основы
нейронных сетей
В этой лекции мы дадим краткий обзор предварительных сведений,
требующихся для того, чтобы дальше перейти непосредственно к
нейронным сетям. А именно, мы рассмотрим:
• основы теории вероятностей, теорему Байеса и вероятностный подход к
машинному обучению;
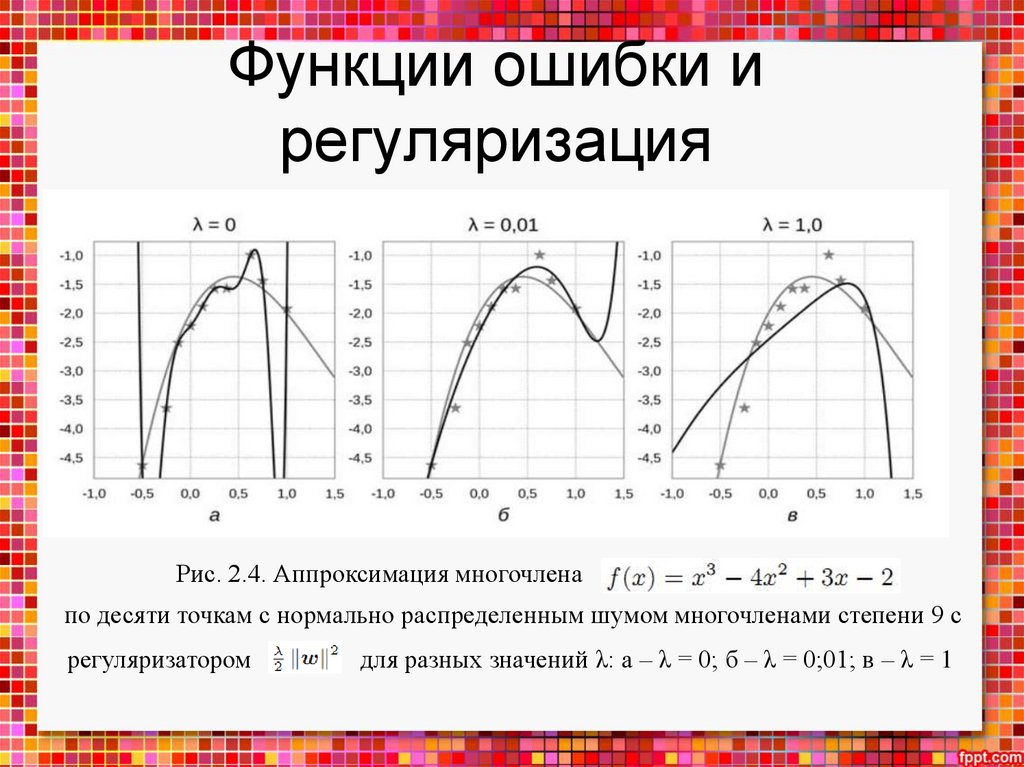
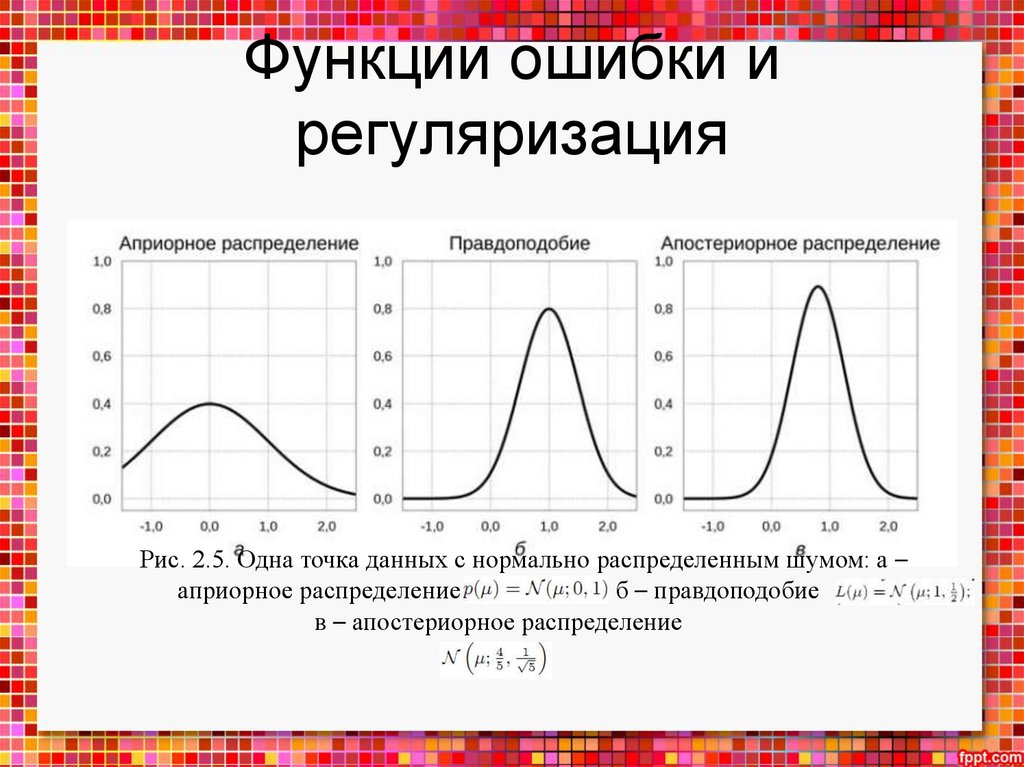
• функции ошибки в машинном обучении и регуляризацию;
• различие между регрессией и классификацией, функции ошибки для
классификации;
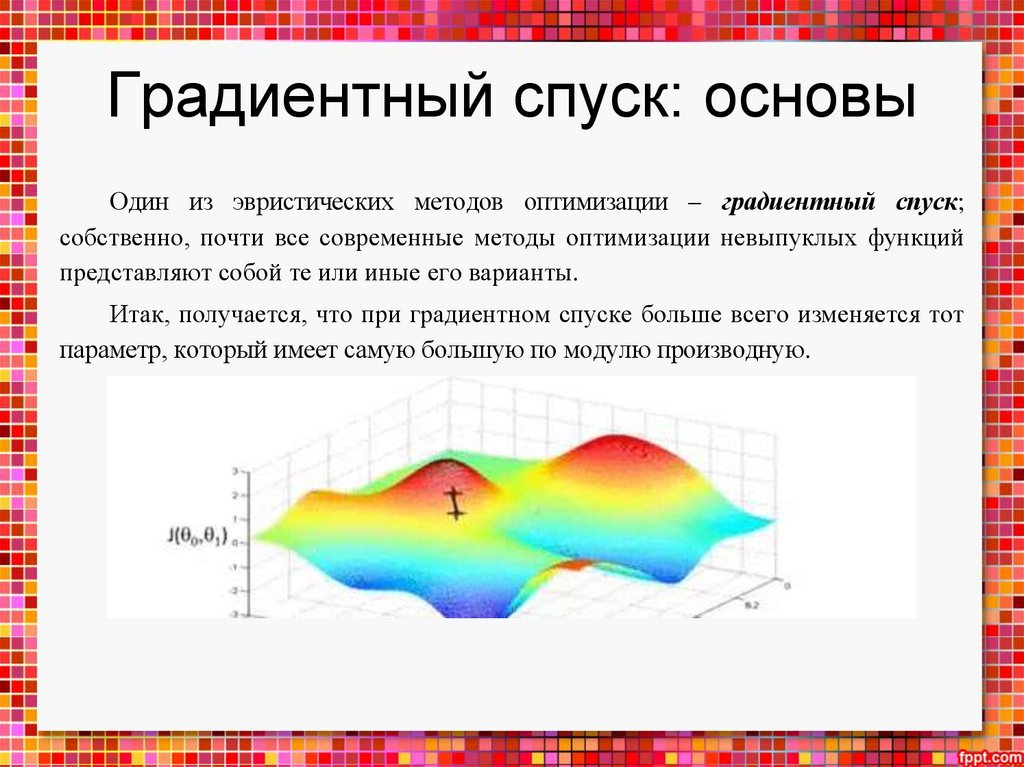
• главный метод оптимизации в нейронных сетях – градиентный спуск;
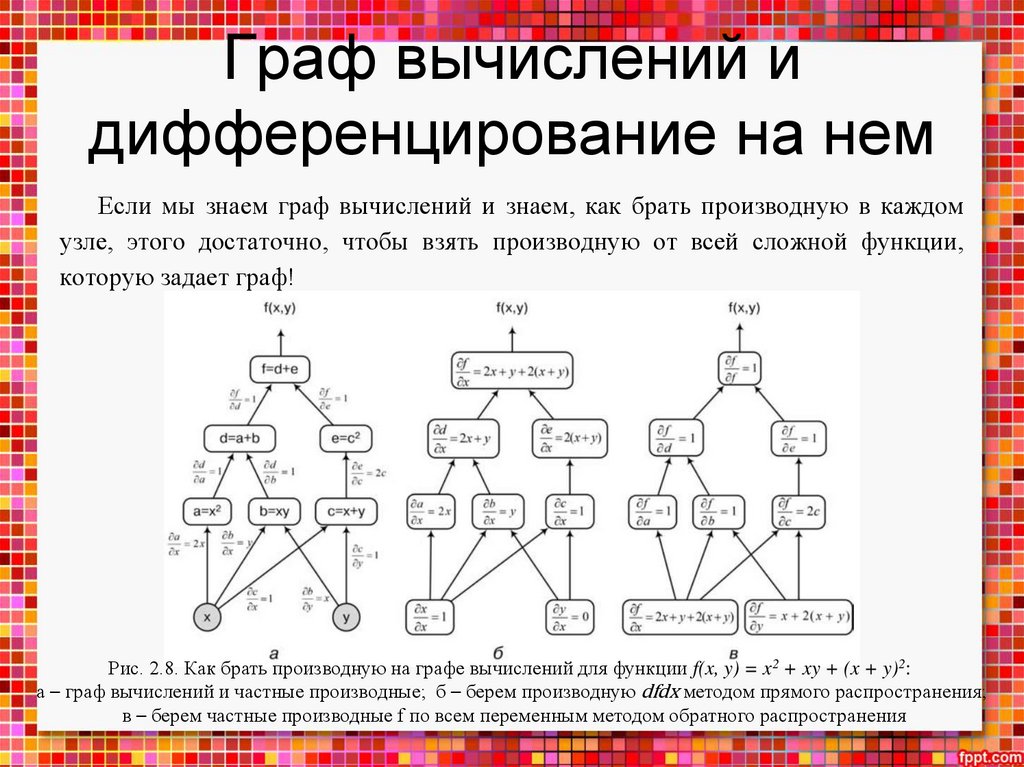
• конструкцию графа вычислений и алгоритмы дифференцирования на
нем.

5.

Математические основы
нейронных сетей
Николенко С., Кадурин А.,
Архангельская Е. Глубокое
обучение. — СПб.: Питер,
2018. — 480 с.:

6.

Теорема Байеса
Прежде всего, машинное обучение – это наука о том, как на
основании данных делать выводы, откуда эти данные взялись, и
предсказания, какие данные встретятся нам в будущем.
Важно, что делать точные выводы невозможно: процессы,
приводящие к порождению данных, слишком сложны даже в самых
простых случаях. Наши модели всегда, неизбежно будут содержать
некоторую долю неопределенности; а математическое описание
неопределенности и операций с неопределенными величинами дает как
раз теория вероятностей.

7.

Теорема Байеса
когда на теорию вероятностей начали смотреть как на теорию меры,
был сделан один из важнейших шагов к формализации первой:
аксиоматика Колмогорова поразительно похожа на аксиомы теории
меры, и этот единый взгляд позволил сильно развить теорию
вероятностей как науку
Колмогоров, Андрей Николаевич (1903–1987) – советский математик, один
из величайших математиков XX века. Колмогоров – буквально создатель
всей современной теории вероятностей; он первым сформулировал
аксиоматику теории вероятностей, основанную на теории меры, и доказал
ряд основополагающих результатов. В искусственный интеллект Колмогоров
верил; в статье он писал, что «принципиальная возможность создания
полноценных живых существ, построенных полностью на дискретных
(цифровых) механизмах переработки информации и управления, не
противоречит принципам материалистической диалектики».

8.

Теорема Байеса
Для дальнейшего нам вполне достаточно понимать, что:
бывают дискретные случайные величины с конечным или счетным
набором исходов; каждому из своих исходов они присваивают
неотрицательную вероятность, и вероятности исходов в сумме дают
единицу; классический и фактически единственный пример здесь –
бросание кубика;

9.

Теорема Байеса
бывают одномерные непрерывные случайные величины, у которых
набор исходов представляет собой вещественную прямую R; тогда
вероятности отдельных исходов превращаются в функцию
распределения F(a) = p(x < a) и ее производную (в этом месте может
быть много сложностей, но практически всегда в наших примерах
функция F будет непрерывно дифференцируемой), плотность
распределения: