Методы и средства передачи информации. Лекция 7. Часть 1

1.

Лекция №7
по курсу
«Методы и средства передачи информации ч.1»
Лектор: д.т.н., Оцоков Шамиль Алиевич,
email: [email protected]
Москва, 2022

2.

Теория групп
G, , g1 G, g 2 G
1) g1 g 2 G
2) g1 ( g 2 g 3 ) ( g1 g 2 ) g 3
3) e, g e e g g
4) g , g 1 , g g 1 g 1 g e

3.

Теория групп
Примеры конечных групп
Множество целых чисел {0,…4} co сложением по модулю 5: (Z5,+)
(0,1,2,3,4) (1+2) mod 5 = (2 + 1) mod 5

4.

Группа подстановок
Пусть n = 3, тогда множество состоит из следующих
постановок

5.

Группа подстановок
1
a1
1
1
a2
1
2
2
3
3
2
3
3
2
1
a3
2
1
a4
2
2
1
3
3
2
3
3
1
1
a5
3
1
a6
3
2
1
3
2
2
2
3
1
H1 = { a1, a2} – является подгруппой
порядка 2
H2 = { a1, a4, а5 } - является подгруппой
порядка 3

6.

Группа подстановок
1
a2
1
1
a3
2
2 3
3 2
2 3
1 3
1 2 3 1 2 3 1 2 3
a5
a2 a3
1 3 2 2 1 3 3 1 2
1 -> 2,
2 ->3
1 ->3
a3* e = a3
e = a1
a2 * x = e x- должен существовать
1 2 3 1 2 3 1 2 3
a2 x
1
3
2
1
3
2
1
2
3
x a2

7.

Группа подстановок
ai * aj = aj * ai (не всегда) – некоммутативная (не абелевая)
Упражнение 1.
Найти обратную к подстановку к элементу a2.
Упражнение 2.
Показать, что множество перестановок с так введенной операцией
умножения является группой. Эта группа обозначается S3.

8.

Группа подстановок

9.

Группа подстановок

10.

Группа подстановок

11.

Группа подстановок

12.

Группа подстановок

13.

Группа подстановок

14.

Подгруппа

15.

Подгруппа
Подгруппа.
H – подмножество G , которое само является группой
H = {e}
(Z,+) – является группой.
Подгруппы?
2Z – множество четных чисел
(2Z,+) является подгруппой (Z,+)
k принадлежит H
k+k тоже принадлежит H
k 2k, 3k, …, -k, -2k,…
k – наименьшее натур число
a принадлежит H
a = q*k + r, r< k
r = a – q*k r принадлежит H
r=0

16.

Подгруппа
Упражнение 3.
Найти подгруппы H1 , H2 порядка 2 и 3 в S3.
Упражнение 4.
Найти порядок элемента a3.
Порядок элемента x – это такое число n
xn = e
x*x*x…*x = e
x+x+x+…x = e
Мультипликативная группа (если групповая операция умножения)
Аддитивная группа (если групповая операция сложение)
a3 n = a1

17.

Подгруппа
n=2
ord(a3) = 2
1 2 3
a3
2 1 3
1 2 3 1 2 3 1 2 3
a1
a3 a3
2 1 3 2 1 3 1 2 3

18.

Подгруппа
Упражнение 5.
Построить левый смежный класс по подгруппе H1 в S3.
H1 = { a1, a2}
g = a3
a3 H1 = { g*a1, g* a2 } = {a3 * a1, a3 * a2 } = {a3, a4 }
1
a2
1
1
a3
2
2 3
3 2
2 3
1 3
1 2 3 1 2 3 1 2 3
a4
a3 a2
2 1 3 1 3 2 2 3 1

19.

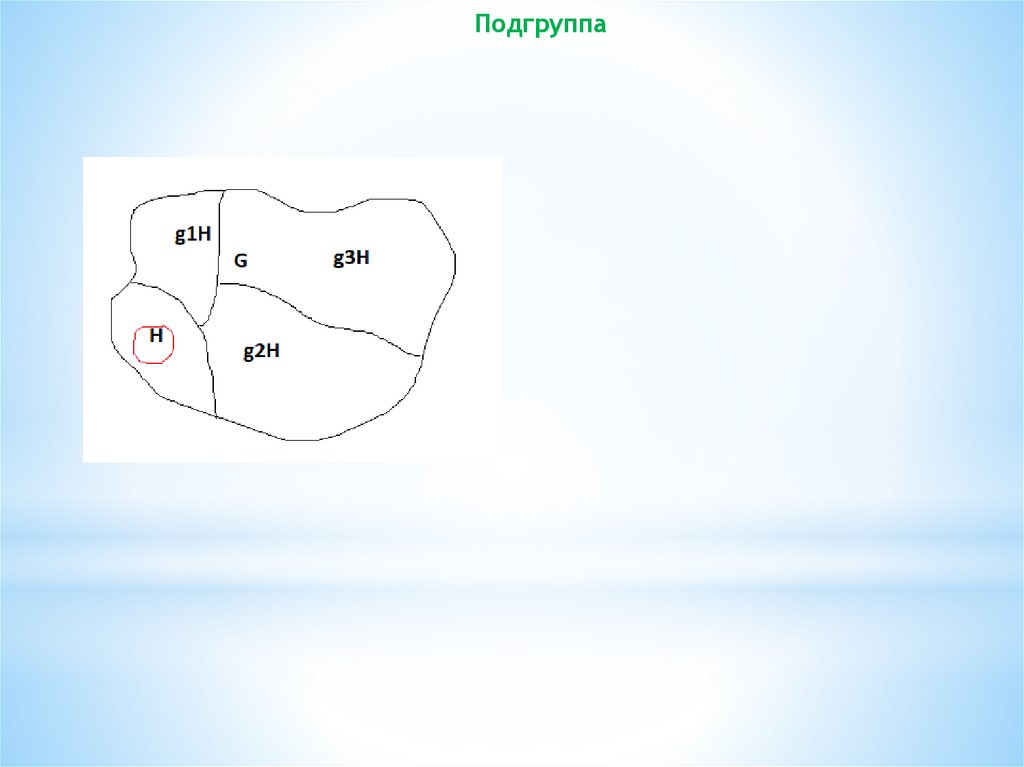
Подгруппа
2 варианта :
Либо совпадают, либо не пересекаются.
Предположим, что существует
x – общий элемент принадлежащий обоим классом
g1H, g2H
x = g1* hk
x = g2 * hl
->
g1*h = g2 * hl
g1 = g2 * hl * (hk ^-1)
hl и h принадл H
hl * (hk^-1) тоже принадлежит H
hl * (hk^-1) = hz принадлежит H
g1 = g2 * hz
g1 H = {g1*h1, g1*h2, g1*h3, …, g1*hn }
g2 H = {g2 * h1, g2 * h2, g2 * h3, …, g2 * hn }

20.

Подгруппа
g1 принадлежит классу g2H
g1* h1, g1* h2, g1* h3,… =
тоже будут принадлежать классу g2H
g1H лежит в классе g2H
g1*hk = g2*hl
g2 = g1*hk*hl^(-1)
g2H лежит в классе g1H
->
g1H = g2H

21.

Подгруппа
Индекс подгруппы H в G = 4
[G:H] = 4
gH = {g*h1, g*h2, g*h3, …, g*hn}
Допустим, что это верно
g* h2 = g* h5
g-1* g* h2 = g-1 * g* h5
h2 = h5
H = { h1, h2, h3, …, hn }

22.

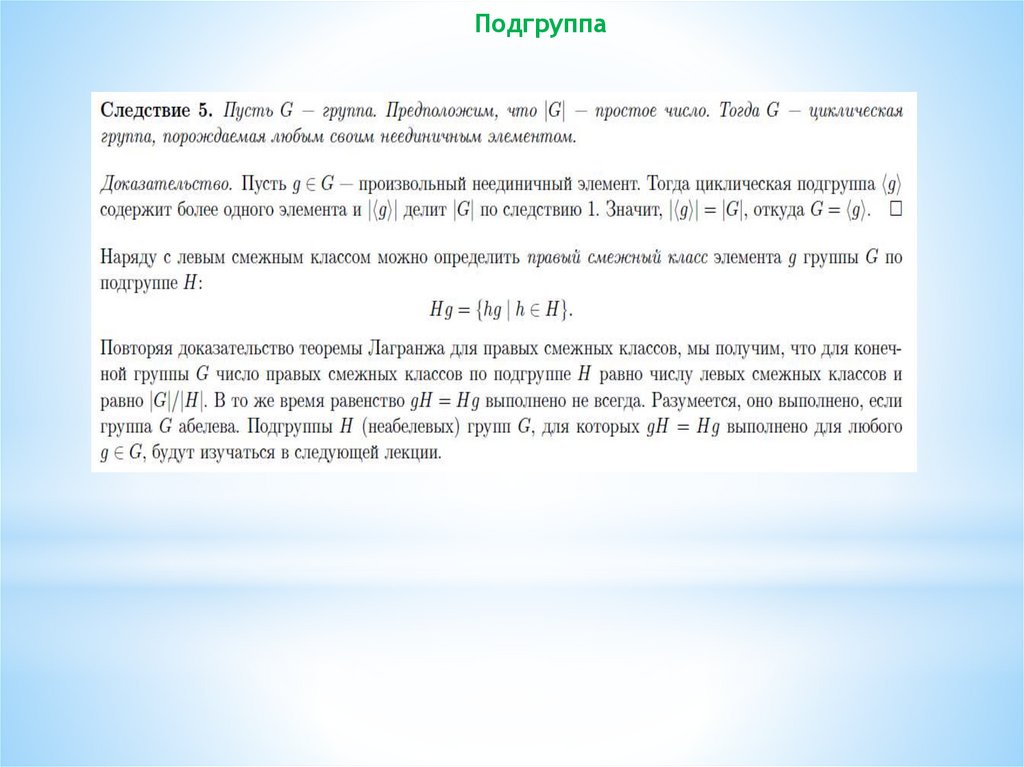
Подгруппа
Порядок группы G = Порядок группы H * индекс [G:H]

23.

Подгруппа

24.

Подгруппа
g
ord(g) - наименьшая степень
gn = e
gord(g) = e по определению порядка элемента
H = { g, g2, g3, … gord(g)-1, e } ord(g)> 3
Допусти g2 = g3
g2 * (g-2) = (g-2 ) g3
e=g
ord g = 1

25.

Подгруппа
Почему H – подгруппа?
gk * gl = g (k+l)
k+l = q*ord(g) + r, r< ord(g)
g (k+l) = g(q*ord(g) + r) = = g (q*ord(g)) * gr = e * gr

26.

Подгруппа
Zp \ 0 – все элементы из Zp без нуля

27.

Подгруппа

28.

Подгруппа

29.

Подгруппа

30.

Подгруппа

31.

Подгруппа
Упражнение 6.
Найти нормальные подгруппы в S3.