Похожие презентации:
Бінарні дерева
1. Бінарні дерева
12.04.2023Всякая вещь есть форма проявления
беспредельного разнообразия.
Козьма Прутков
2. Поняття бінарного дерева
Бінарне дерево - упорядковане дерево степені 2.Властивості:
може бути порожнім;
будь-який вузол може мати другого (правого)
сина за відсутності першого (лівого).
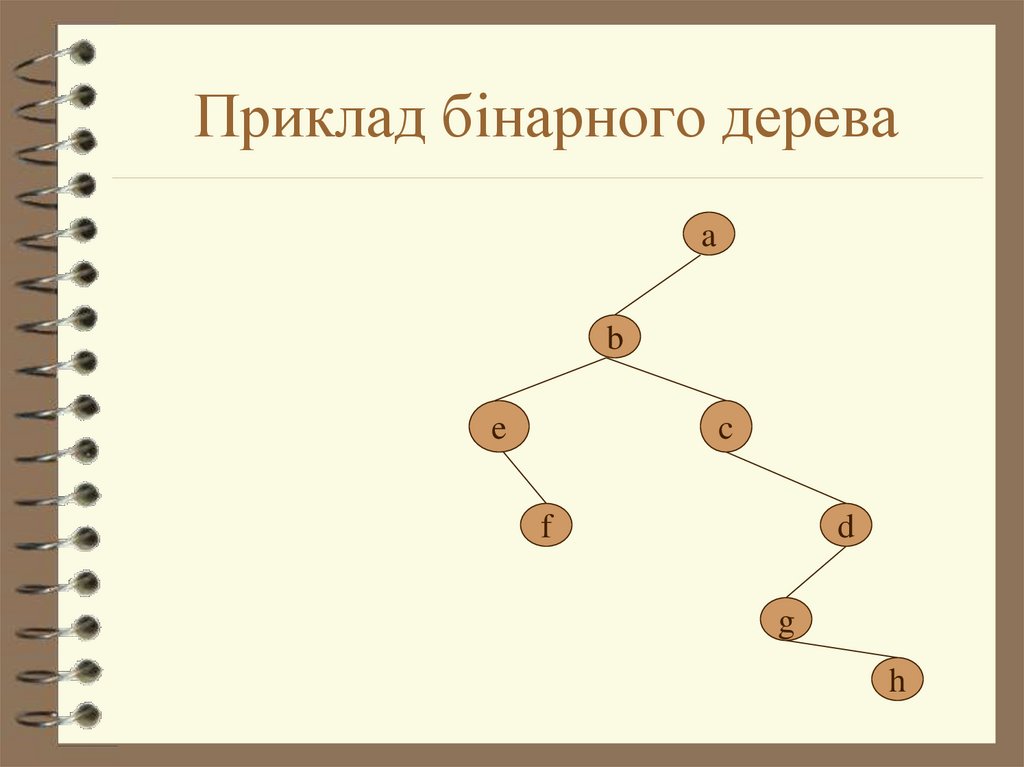
3. Приклад бінарного дерева
ab
e
c
f
d
g
h
4. Зберігання бінарних дерев
Бінарнідерева
звичайним деревам.
зберігаються
аналогічно
При розміщенні в стандартній формі:
typedef struct BTN {int dat;
BTN *lt, *rt;
} BINTRN, *BINTRP;
5. Представлення бінарним деревом
Використовують деякі “традиційні” способипредставлення звичайних дерев (довільної
степені)
бінарними
деревами.
Можна
представляти й послідовності дерев.
Існує взаємно однозначна відповідність між
скінченними
послідовностями
звичайних
впорядкованих дерев та бінарними деревами.
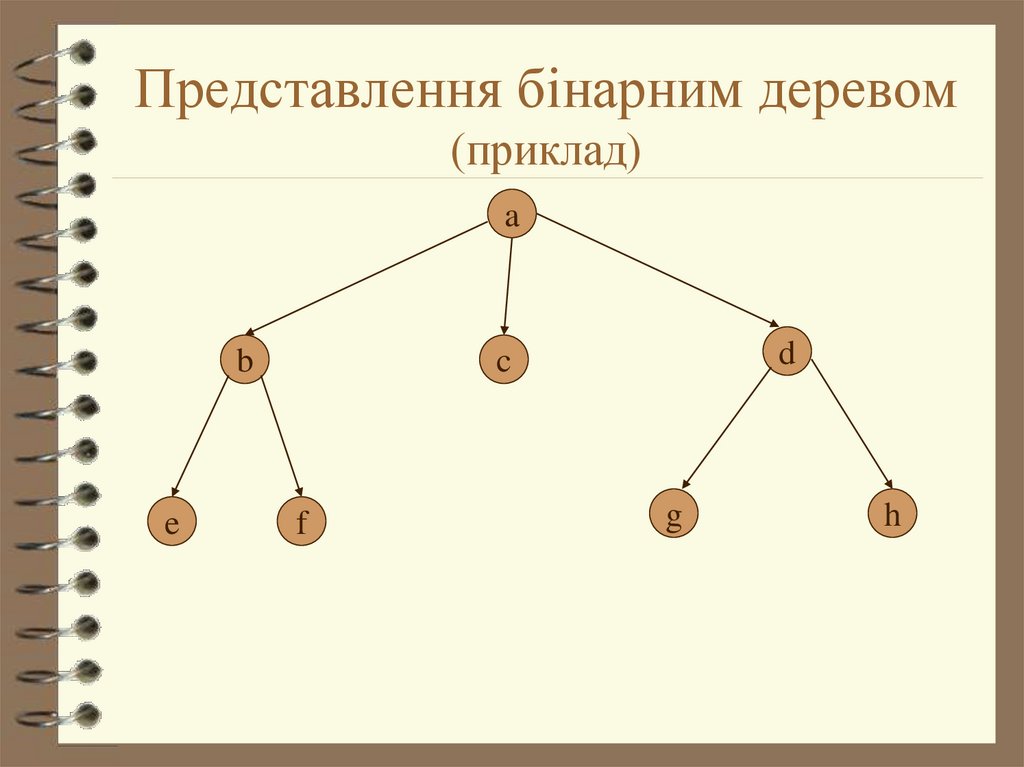
6. Представлення бінарним деревом (приклад)
ab
e
d
c
f
g
h
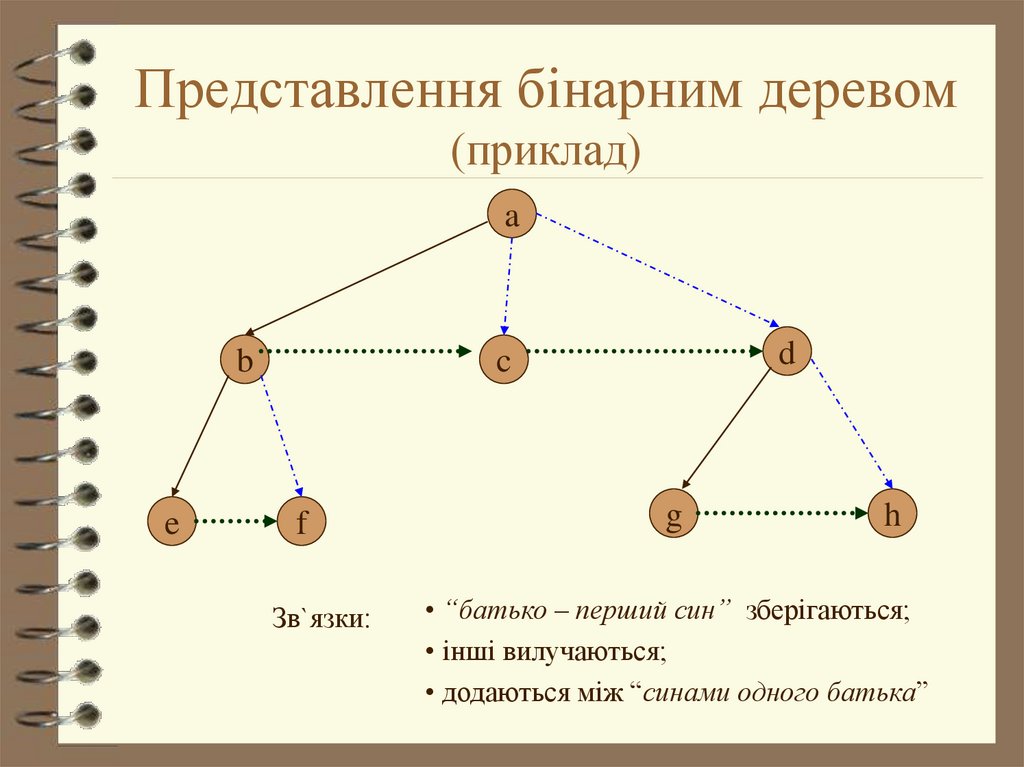
7. Представлення бінарним деревом (приклад)
ab
e
d
c
f
Зв`язки:
g
h
• “батько – перший син” зберігаються;
• інші вилучаються;
• додаються між “синами одного батька”
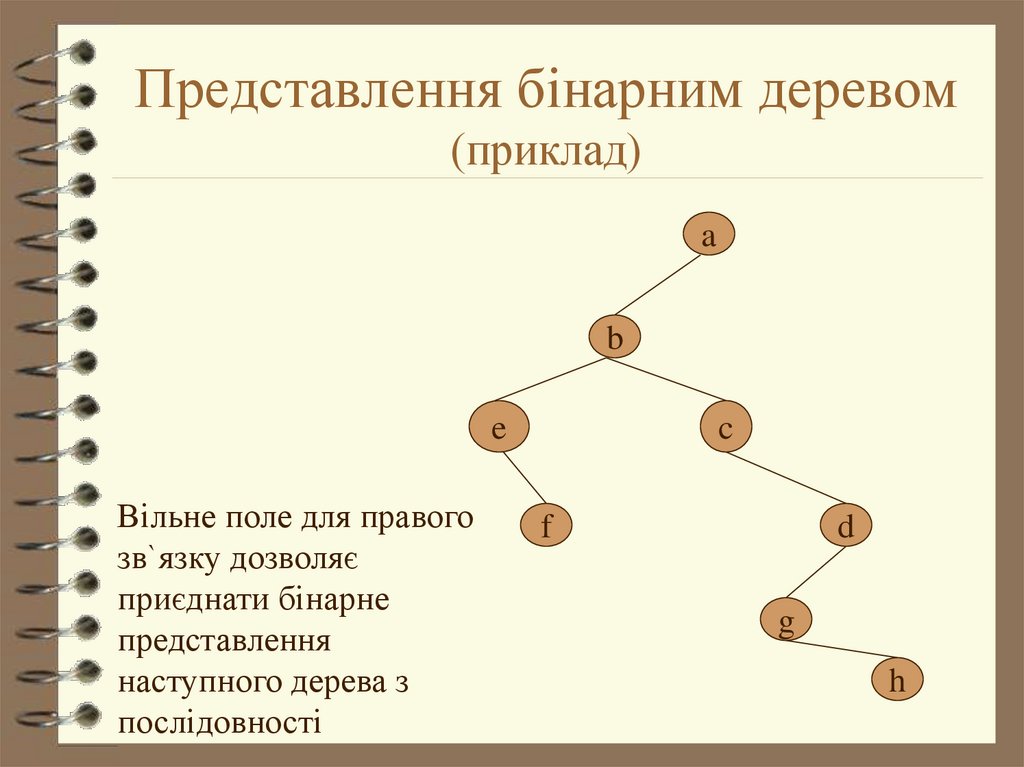
8. Представлення бінарним деревом (приклад)
ab
e
Вільне поле для правого
зв`язку дозволяє
приєднати бінарне
представлення
наступного дерева з
послідовності
c
f
d
g
h
9. Представлення бінарним деревом
Запишемо функцію, що створює відповіднебінарне дерево для послідовності з n≤3 дерев
степені 3.
Типи даних:
const int m = 3;
typedef struct TrNd {int dat;
TrNd *s[m];} TrNde, *TrNdp;
typedef struct BTN {int dat;
BTN *lt, *rt;
} BINTRN, *BINTRP;
10. Представлення бінарним деревом
//перехід від послідовності ≤3 дерев до бінарногоBINTRP beta(TrNdp p, TrNdp q, TrNdp r){
BINTRP t;
if (p) { t = new BINTRN; t->dat = p->dat;
t->lt = beta(p->s[0], p->s[1], p->s[2]);
t->rt = beta(q, r, NULL);}
else t = NULL;
return t;
}
11. Проходження бінарних дерев
Систематичний перегляд всіх вузлів дерева упевному порядку:
Прямий порядок;
Обернений порядок;
Симетричний порядок:
– проходимо у симетричному порядку ліве
піддерево;
– проходимо корінь;
– проходимо у симетричному порядку праве
піддерево.
12. Симетричний порядок
– проходимо у симетричномупорядку ліве піддерево;
– проходимо корінь;
b
– проходимо у
e
симетричному
порядку праве
f
піддерево.
a
c
d
g
<e, f, b, c, g, h, d, a>
h
13. Симетричний порядок
//дерево подано в стандартній форміvoid symord(BINTRP p){
if (p) {
symord(p->lt);
cout << p->dat << “, “; //обробка вузла
symord(p->rt);
}
}
14. Приклад
Побудуємо бінарне дерево з максимальносиметричною структурою для заданої кількості
вузлів. Роздрукуємо відмітки вузлів згідно
симетричного порядку.
Правило рівномірного розподілу n вузлів
можна визначити рекурсивно:
перший вузол – корінь дерева;
створюємо ліве піддерево з кількістю вузлів
nleft = n div 2 ;
створюємо праве піддерево з кількістю вузлів
nright = n – nleft – 1 .
Pr_1
15. Створення симетричного бінарного дерева
BINTRP build(int nn){BINTRP p; int dd, nleft, nright;
if (!nn) return NULL; //порожнє дерево
nleft = nn /2; //кількість вузлів у лівому
nright = nn - nleft - 1; //кількість вузлів у правому
cout << "Enter node data: "; cin >> dd; cout << endl;
p = new BINTRN; p->dat = dd; //створюємо корінь
p->lt = build(nleft); //будуємо ліве
p->rt = build(nright); //будуємо праве
return p;}
16. Спеціальні способи зберігання
Прошите дерево будується з бінарного деревашляхом заміни NULL-покажчиків:
NULL-покажчик на лівого сина замінюється
покажчиком на попередній вузол у симетричному
порядку;
NULL-покажчик на правого сина - покажчиком
на наступний вузол у тому ж порядку;
щоб відрізнити “нитки” від звичайних
покажчиків, використовують два додаткових поля
в кожному вузлі прошитого бінарного дерева;
прив`язка до порядку обходу.
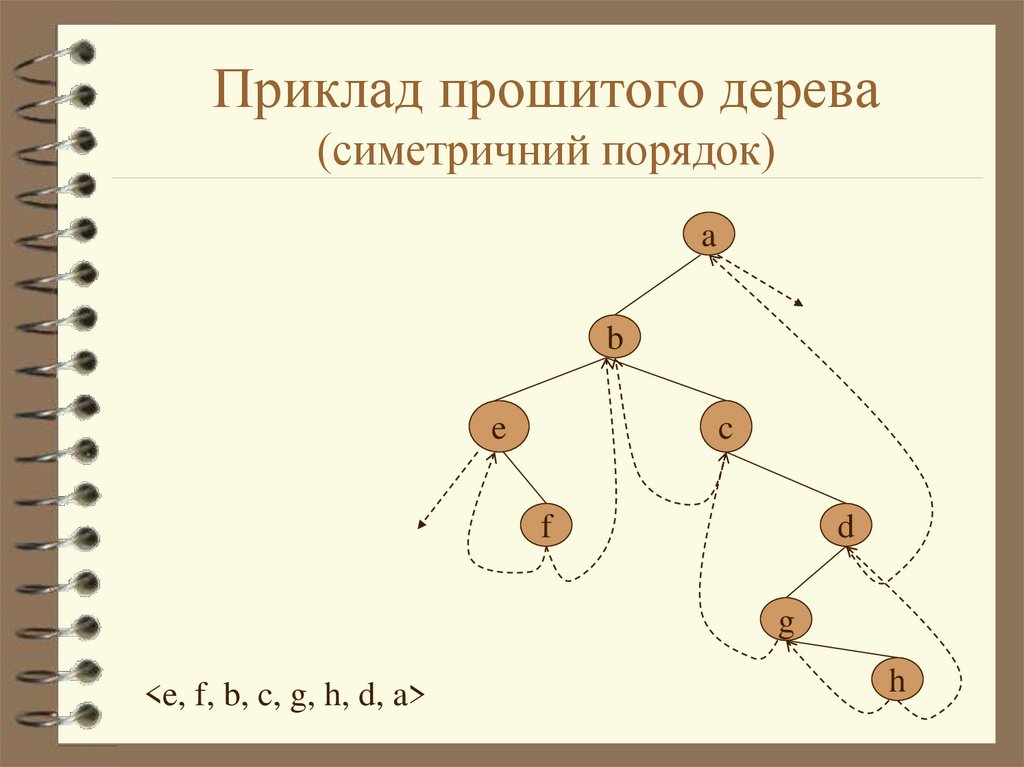
17. Приклад прошитого дерева (симетричний порядок)
ab
e
c
f
d
g
<e, f, b, c, g, h, d, a>
h
18. Прошиті дерева (симетричний порядок)
Структура вузла та покажчик визначаються:typedef struct TH {int dat;
TH *lt, *rt;
bool li, ri;
} THN , * THP;
Якщо p->li то p->lt - показує на лівого сина,
інакше на попередній вузол у симетричному
порядку. Аналогічно p->rt - показує на правого
сина, або на наступний вузол (залежить від
p->ri ).
Pr_2
19. Проходження прошитого дерева (симетричний порядок)
void symm(THP p){while (p->li) p = p->lt;
while (p) {
cout << p->dat << ", "; p = suc(p);}
}
THP suc(THP p){
THP q=p->rt;
if (p->ri)
while (q->li) q = q->lt;
return q;}
20. Побудова прошитого дерева (симетричний порядок)
//створення прошитого дерева//за звичайним бінарним деревом
THP buildh(BINTRP p){
return (p ? buildo(p, NULL, NULL) : NULL);
}
21. Побудова прошитого дерева (симетричний порядок)
THP buildo(BINTRP p, THP sl, THP sr){THP t;
t = new TH;
t->dat = p->dat;
if ((t->li = (p->lt != NULL)))
t->lt = buildo(p->lt, sl, t);
else t->lt = sl;
if ((t->ri = (p->rt != NULL)))
t->rt = buildo(p->rt, t, sr);
else t->rt = sr;
return t;}
22. Послідовні способи зберігання
Можливе також зберігання організоване вмасиві структур з розміщенням вузлів дерева в
прямому порядку.
Лівий син вузла p, якщо він існує, завжди
розміщується поряд з p, а місцезнаходження
правого сина вказується певним значенням в
структурі (r). Наявність чи відсутність лівого
сина фіксується в структурі логічним полем (isl).
23. Послідовні способи зберігання (представлення)
Потрібні типи даних та змінні:const int M=100;
struct {int dat; unsigned int r;
bool isl;} BTR[M];
int n;
// n – кількість вузлів у дереві
// M – обмеження на кількість вузлів у дереві
// isl – ознака існування лівого сина
// r – вказує на розташування правого сина
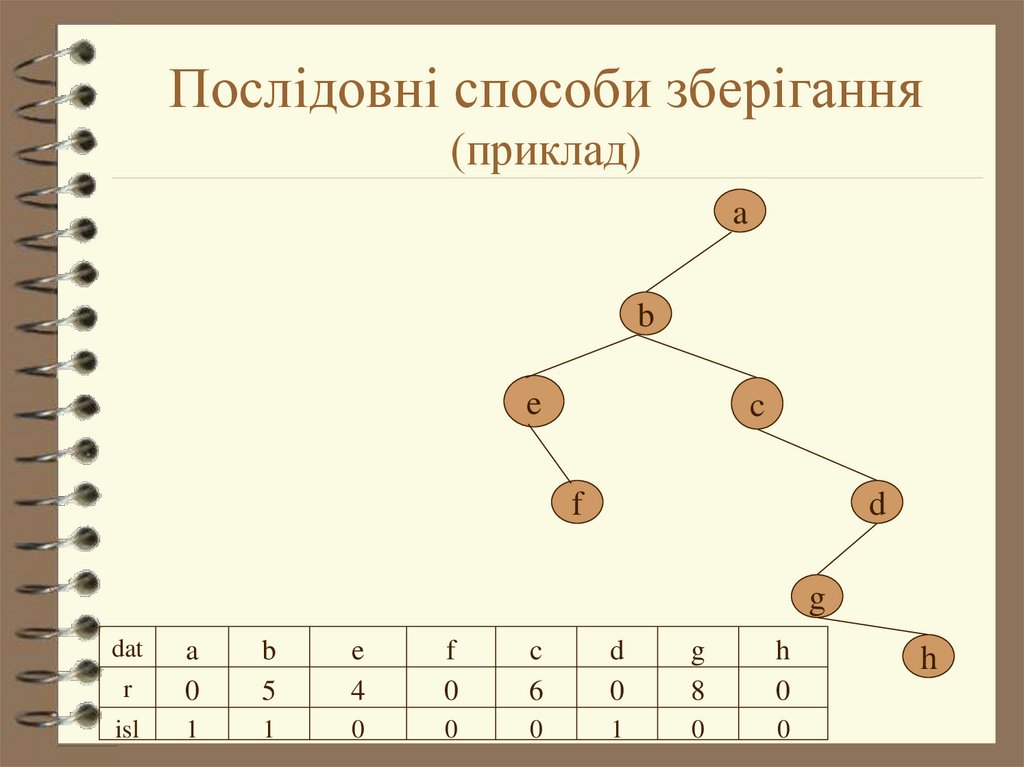
24. Послідовні способи зберігання (приклад)
ab
e
c
f
d
g
dat
r
a
0
b
5
e
4
f
0
c
6
d
0
g
8
h
0
isl
1
1
0
0
0
1
0
0
h
25. Послідовні способи зберігання (дії)
Для вузла з індексом i (0≤i≤n) визначення вузла jз певною умовою (за його відсутністю – j=-1):
лівого сина - j = (BTR[i].isl ? i+1 : -1);
правого сина - j = BTR[i].r-1;
наступного вузла у прямому порядку
j = ((i<n-1) ? i+1 : -1);
попереднього вузла у прямому порядку j = i-1;
батька - if (i) { j = i-1; if (!BTR[j].isl)
while (BTR[j].r != i+1) j--;
}else j = -1;
26. Зауваження
У розглянутих прикладах обмежились лишенайбільш
принциповими
способами
представлення бінарних дерев та здійснення
обробки даних, що представлені деревом.
“Прошивка” бінарного дерева залежить від
обраного способу обходу й спрощує подальші
дії, що основані на цьому способі обходу.
Повністю
аналогічним
чином
можна
організувати обхід “прошитого” дерева у
відповідному порядку, починаючи з останнього.
27. Підсумки
Внаслідок важливості бінарних дерев, окреморозглянули основні підходи до їх представлення
а також здійснення основних дій.
Розглянули
можливість
представлення
“звичайних” дерев, а також їх послідовностей,
бінарними деревами.
28. Поради
Обирати(у разі можливості) найбільш
адекватний спосіб представлення бінарних дерев,
виходячи насамперед з наступних потрібних дій.
Розібратися з термінологією.
Розібратися як з рекурсивними, так й з
нерекурсивними способами здійснення обробки
даних представлених бінарними деревами.
29. Задачі
Написати функції для визначення у бінарномудереві, яке подане у стандартній формі
– висоти;
– кількості листів;
– кількості вузлів;
– вузла з заданим значенням;
– значення найбільшого елемента у вузлах.
Написати функцію для звільнення всіх ділянок
пам`яті, зайнятих вузлами бінарного дерева,
поданого у стандартній формі.
Написати функцію, що будує копію бін. дерева.
30. Задачі
Написатинерекурсивну
функцію
для
визначення кількості вузлів у прошитому дереві.
Написати
нерекурсивні
функції
для
проходження прошитого дерева в симетричному
порядку, починаючи з останнього.
Написати
нерекурсивну
функцію
(з
використанням стека) для друкування вузлів
бінарного дерева, поданого у стандартній формі,
при його проходженні:
– в симетричному порядку;
– в оберненому порядку.
























 Математика
Математика Информатика
Информатика








