Спектральний аналіз. Ряд та інтеграл Фур’є

1.

Київський національний університет
імені Тараса Шевченка
Спектральний аналіз
професор Вижва Зоя Олександрівна

2. Література

• 1.Блейхут Р. Быстрые алгоритмы цифровой обработки
сигналов. М., 1989.
• 2.Бат М. Спектральный анализ в геофизике. М., 1979.
• 3.Залманзон Л.А. Преобразования Фурье, Уолша, Хаара и их
применение в управлении, связи других областях. М., 1989.
• 4. Харкевич А.А. Спектры и анализ. М. , 5 изд., 2009.
• 5. Ядренко М.И. Спектральная теория случайных полей. - К.,
“Вища школа”,- 1980,- 208 с.
• 6. Вижва З.О. Статистичне моделювання випадкових
процесів та полів. Монографія, - К.: ВГЛ “Обрії”, - 2011.
• 7.Бендат Дж., Пирсол А. Прикладной анализ случайных
данных. М. ,1989.
• 8.Марал С.Л. Цифровой спектральный анализ и его
приложение. М. 1990.

3. Лекція 1. Ряд та інтеграл Фур ’ є

Означення . Функція f(t) називається періодичною з
періодом Т, якщо:
f (t ) f (t nT ), n Z .
•1. Ряд Фур’є в дійснозначній формі
t
f t c0 ck cos (2k k ),
T
(1)
k 1
де ск –амплітуда синусоїдального коливання, k
початкова фаза.
f t c0
k 1
t
t
(ak cos 2k bk sin 2k ), (2)
T
T
Де
2
2
ak ck cos k , bk ck sin k , ck ak bk ,
bk
tg k .
ak (3)

4. Коефіцієнти Фур’є

2
ak
T
T /2
T /2
T /2
t
2
t
f t cos 2k d t , bk f t sin 2k d t.
T
T T /2
T
1
c0
T
N
f t c0
k 1
(4)
T /2
f t
dt
T /2
t
t (5)
(ak cos 2k bk sin 2k ),
T
T
•2. Ряд Фур’є в комплексній формі
f t
k
t
Ck exp (i 2k ),
T
2Ck ck exp( i k ) ak ibk ,2 Ck ck , C0 c0 .
(6)
(7)

5. Комплексні амплітуди

1
Ck
T
T /2
T /2
t
f t exp( i 2k ) d t .
T
(8)
Підставимо (8) в (6):
1
f t
T
t
exp (i 2k )
T
k
w1 dw;
1
f t
2
T /2
t
f t exp( i 2k ) d t ,
T
2
w1
T
•Кругова частота
T ;
T /2
k
2 w,
T
(10)
w- поточна частота
(11)
exp ( iwt ) dw f t
(9)
exp( iwt ) d t ,

6. Інтеграл Фур ’ є

1
f t
2
S (w) exp ( iwt ) dw ,
(12)
Інтеграл Фур ’ є в комплексній формі
•де
S w
f t
exp( iwt ) d t ,
(13)
Спектр, або обернене перетворення Фур ’ є .
1
dС S ( w)dw.
комплексна амплітуда кожного коливання
(14)

7. Лекція 2. Спектри: означення та класифікація

Якщо розглянути ряд Фур’є в формі (1) та записати в вигляді:
(15)
f t c0
c
k
cos (kw1t k ),
k 1
де w1 - основна частота (10):
2
w1 ,
то сукупність величин { ck } називається спектром
амплітуд, а
T
сукупність величин {φk} називається спектром фаз.
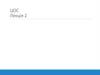
Спектр періодичної функції:
1.Лінійчатий (дискретний);
2.Гармонічний.
Дискретний спектр є і в неперіодичної функції: накладення
двох синусів з частотами w1 та
w1
2

8. .

9. Спектр неперіодичної функції

Інтеграл Фур ’ є ( лекція 1)
1
f t
2
S (w) exp ( iwt ) dw ,
(12)
Підінтегральна функція є коливання з нескінченно малою
амплітудою dC:
1
(16)
S ( w)exp ( iwt )dw dС exp ( iwt ).
Звідси S(w) - не безпосередньо амплітуда, а так звана
спектральна щільність:
S ( w) dС / dw.
(17)
Модуль цієї величини називають просто спектром:
Ф( w) S ( w) .
(18)

10. Теореми про спектри

1. Спектр суми функцій дорівнює сумі їх спектрів:
S1 w S2 w
[ f t f t ] exp( iwt ) d t,
1
2
(19)
2. Спектр похідної від функції f‘(t)= df/dt :
S(1) w f ' t r exp( iwt ) d t ,
2
проінтегруємо частинами:
Для n-ї похідної:
(22)
Отже:
S(1) w f t exp( iwt ) | iw f t exp( iwt ) d t ,
S(1) w iwS w .
S( n ) w ( iw)n S w .
(20)
(21)

11. Теореми про спектри

3. Спектр інтеграла від функції:
t
S( 1) w
exp( iwt )( f
d )dt(23)
,
проінтегруємо частинами і отримаємо:
(24)
S( 1) w (1/ iw) S
при умові:
w ,
4. Спектр функції з запізненням:
f t
d t 0.
t
після заміни
S змінної
w t1=t-τ
exp(отримаємо:
iwt ) f t
S w exp( iwt ) S w .
(25)
d t ,(26)

12. Теореми про спектри

Якщо перейти від комплексних спектрів до модулів, то
S ( w) Ф ( w) Ф( w).
(27)
5. Транспозиція спектрів
на Ω:
S w
f t exp( i ( w )t ) d t ,
(28)
Отже, такий спектр відповідає функції:
f t f t exp( i t ) ,
(29)
6. Спектр добутку функцій f1(t), f1(t) дорівнює згортці спектрів:
f t f t exp( iwt ) d t S S w d ,
1
2
1
2
(30)

13. Теореми про спектри

6. Спектр згортки функцій f1(t), f1(t) дорівнює добутку спектрів:
f (t ) f1 f 2 t d .
(31)
S w exp( iwt ) d t f1 f 2 t d
f1 d f 2 t exp( iwt ) d t
після заміни змінних
tмаємо:
exp( iw ) f1 d f 2 exp( iw ) d S1 w S2 w .
(32)

14. Лекція 3. Поточний спектр

Означення. Поточним спектром називається функція не тільки від
частоти, але і від часу:
(1)
t
(2)
St
Приклад.
w f ( )exp( iw ) d .
t
St w f ( )exp( iw ) d .
(3)
0
t
f t sin t.
St w sin t exp( iw ) d
0
w
[1 exp( iwt )(cos t i sin t )].
w

15. .

Нехай tn=nT/2=n π /Ω (T=2
1
St w
π/ Ω), тоді
1
w
sin n
, при парному n;
2
2
w
1
1
St w
1
w
cos n
,
2
2
w
1
при непарному n.

16.

17. Миттєвий спектр

Означення. Миттєвим спектром називається функція не тільки від
частоти, але і від часу:
(4)
t
(5)
вагова
S функція:
w, t
Т
f ( ) exp((6) iw )(7)d .
t
(8)
t Т
Sr w, t r ( t ) f ( )exp( iw ) d .
0
r x ( x Т ) ( x).
0, x 0,
x
1, x 0.
r x exp(ax) ( x).

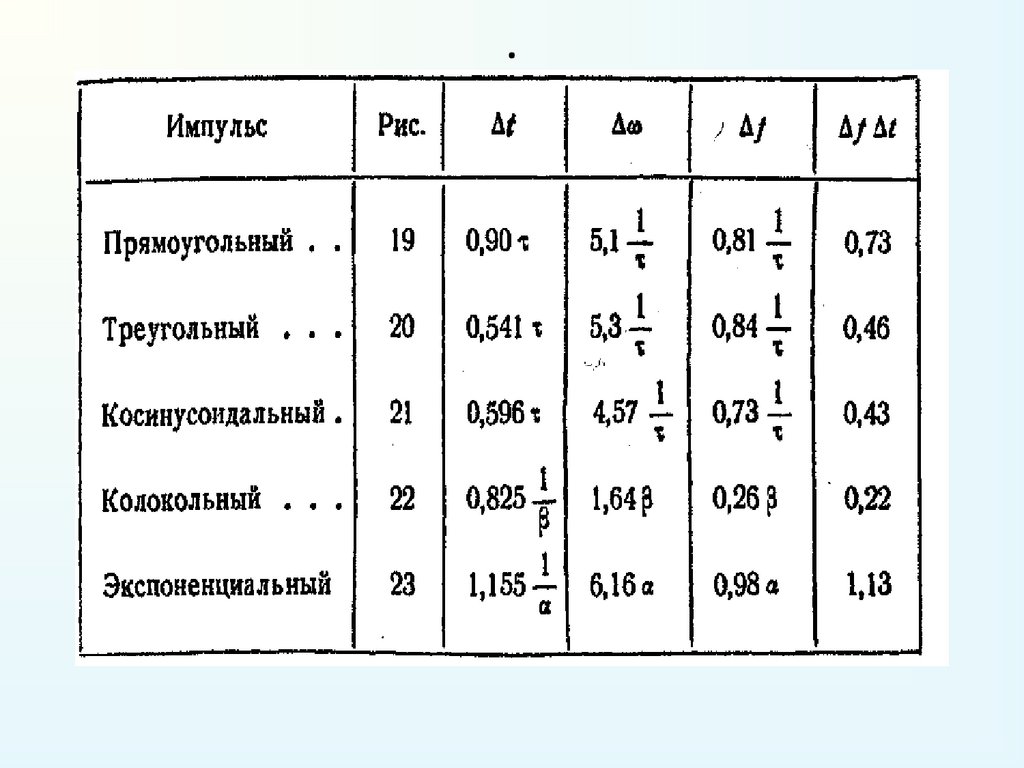
18. Лекція 4. Спектри деяких імпульсів

0, t 0
1
(t ) , t 0 ,
2
1, t 0 .
1. Одинична функція:
(1)
Дельта- функція, або функція одиничного імпульсу:
Спектр:
S w
d
t
(t ) ,
dt
(2)
t
exp( iwt ) d t exp( iw ).
(3)

19. .

2. Прямокутний імпульс:
0 , t / 2
f (t ) h , / 2 t / 2 ,
0, t / 2 .
Спектр:
2
S1 w h
q=hτ.
2
(4)
sin w
2.
exp( iwt ) d t q
(5)
w
2 де

20. .

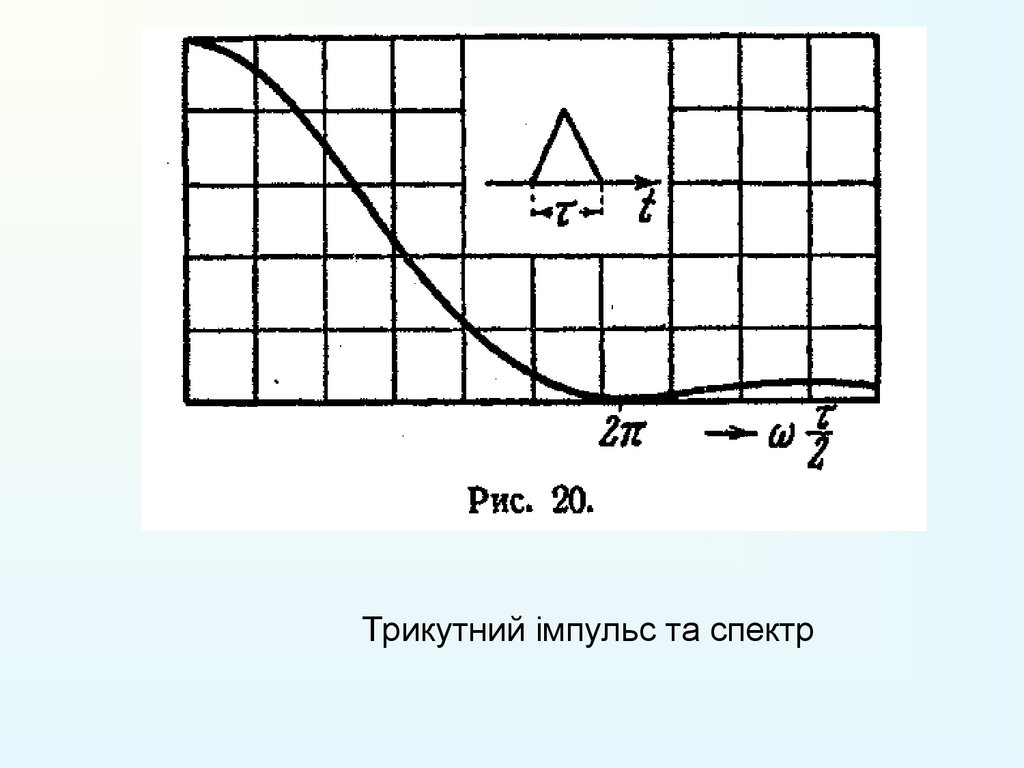
3. Трикутний імпульс:
Спектр:
де q= hτ /2.
.
(6)
0 , t / 2;
h(1 2t ) , / 2 t 0;
f (t ) (7)
h(1 2t ), 0 t / 2 ;
0, t / 2 .
0
2t
S1 w h (1 ) exp( iwt ) d t
2
1 cos w
2t
2.
h (1 ) exp( iwt ) d t q
1 2
0
(w )
2 2
2

21. .

4. Косинусоїдальний імпульс:
0 , t / 2
t
f (t ) h cos , / 2 t / 2 ,
(9)
0, t / 2 .
Спектр:
де q=2hτ/π.
cos w
t
2 .
S w h cos exp( iwt ) d t q
2 2
( w )
2
2
2
(8)

22. .

5. Дзвінковий імпульс:
Спектр:
(10)
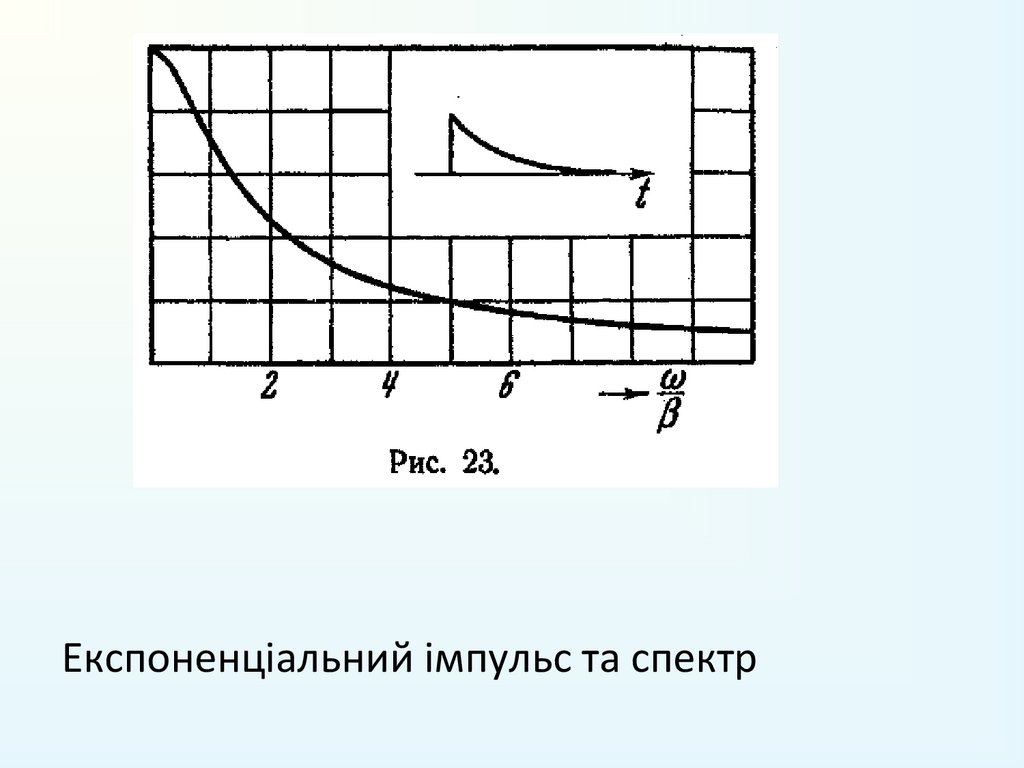
6. Експоненціальний імпульс:
(11)
f(12)
(t ) exp(
(13)
Спектр:
2 t 2 ).
S w exp( t ) exp( iwt ) d t
exp( w2 / 4 2 ).
2 2
f (t ) exp( t ) 0 (t ).
1
S w exp( ( iw)t ) d t
.
iw
0

23. .

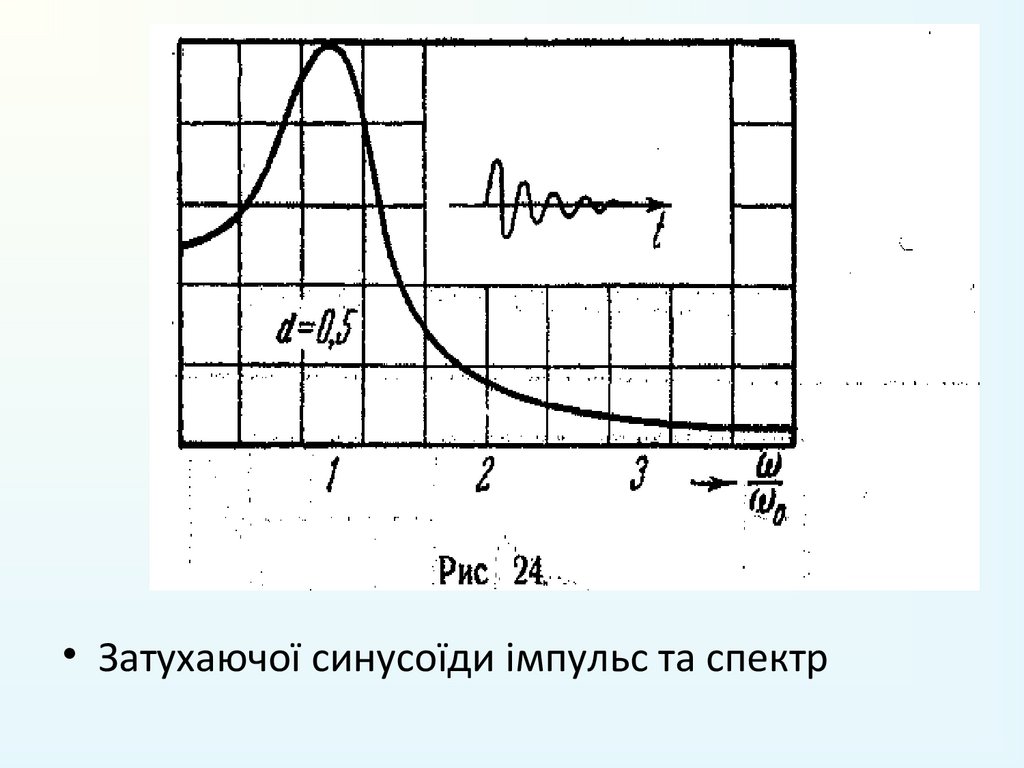
7. Затухаючої синусоїди імпульс:
(14)
Спектр:
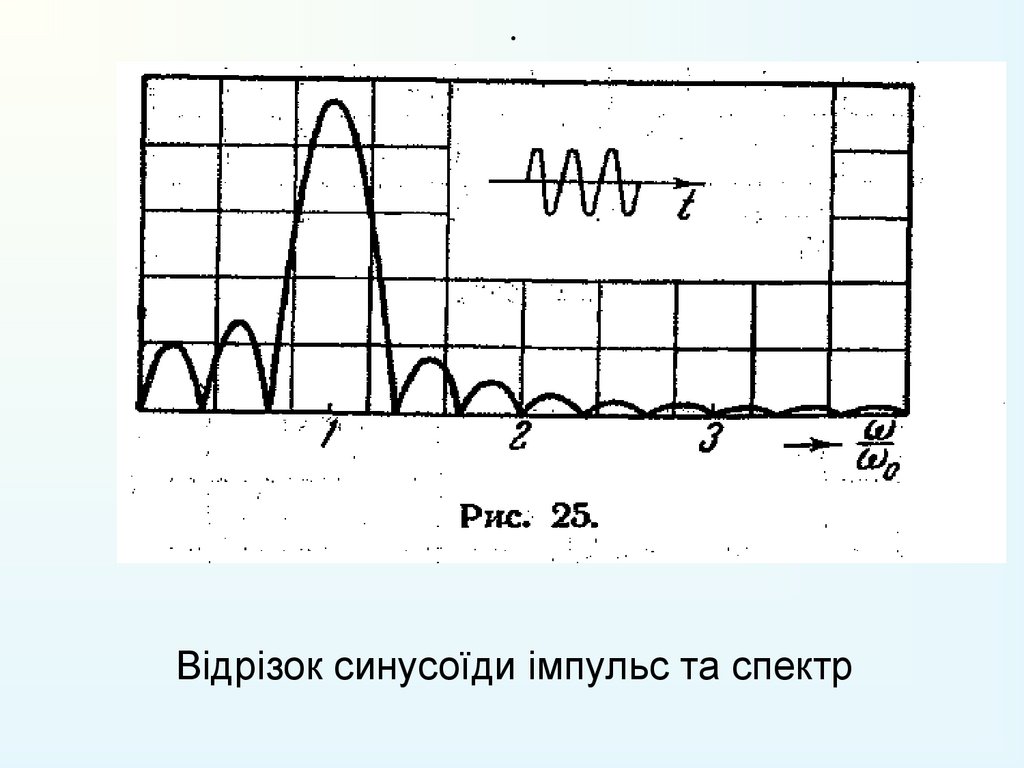
(15) 8. Відрізок синусоїди імпульс :
f (t ) exp((16)
t ) sin w1t 0 (t ).
w1
S w exp( ( iw)t )sin w1t d t 2 2
.
2
w w1 2i w
0
Спектр:
(17)
0 , t nT / 2
f (t ) sin w0t , nT / 2 t nT / 2 ,
0, t nT / 2 .
nT /2
2iw0
w
n
S w sin w0t exp( iwt ) d t 2 2 ( 1) sin n .
w0 w
w0
nT /2

24. .

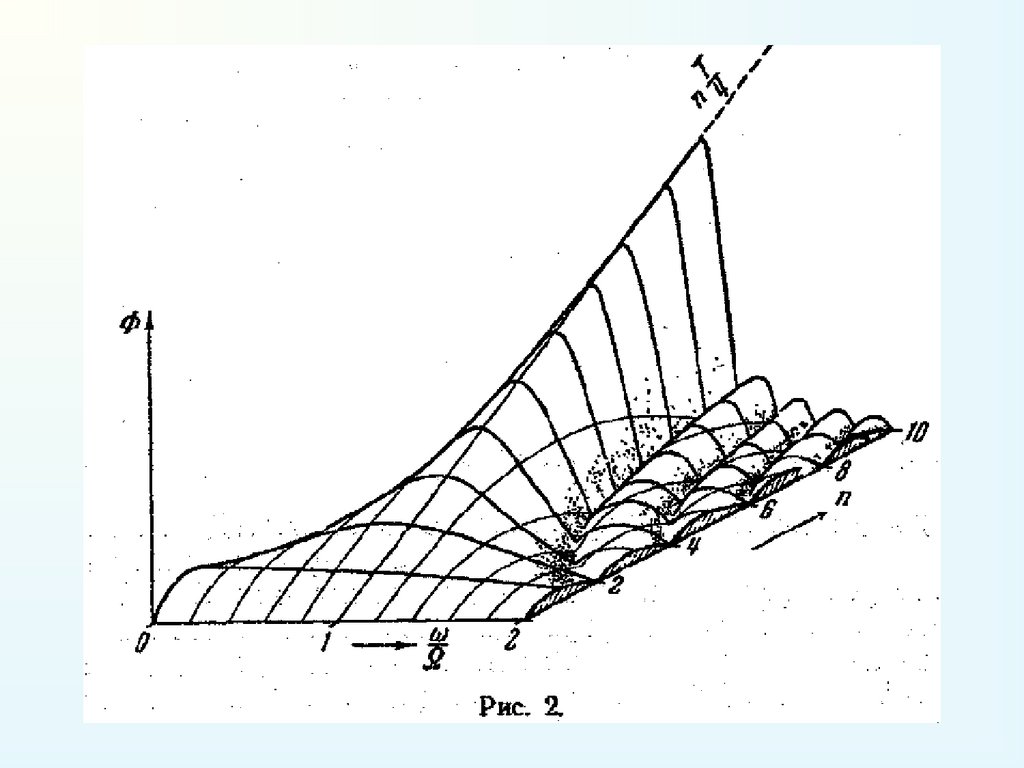
Прямокутний імпульс та спектр

25. .

Трикутний імпульс та спектр

26. .

Косинусоїдальний імпульс та спектр

27. .

Дзвінковий імпульс та спектр

28. .

Експоненціальний імпульс та спектр

29. .

• Затухаючої синусоїди імпульс та спектр

30. .

Відрізок синусоїди імпульс та спектр

31. Лекція 5. Зв’язок між довжиною імпульса та шириною спектра

Нехай для функції f(x) із спектром S(w) змінимо масштаб
часу в а разів і знайдемо спектр функції а f(а x) :
(1)
w
СпектрSдляwпрямокутного
імпульсу:
а
f аt exp( iwt ) d t S .
a
а (3) де
(2) Перший нуль
спектра буде:
,
Δf – ширина спектра, Δ t - довжина імпульса .
Тоді
(4)
sin w
S1 w q
t
t
w
2 f
2
2
f t 1.
2
w
2

32. .

Спектр для трикутного імпульсу:
Перший нуль спектра буде:
1 cos w
2.
S ( w) q
1 2
(w )
2 2
(5)
t
2 f
2
2
(6)
де Δf – ширина спектра, Δ t - довжина імпульса .
f t 2.
Тоді
,
(7)

33. .

Спектр для косинусоїдального імпульсу:
cos w
2 .
S w q
2 2
( w )
2
(8)
Перший нуль спектра буде:
t
2 f
1.5
2
(9)
де Δf – ширина спектра, Δ t - довжина імпульса .
f t 1.5.
Тоді
,
(10)

34. .

Експоненціальний імпульс:
f (t ) exp( t ) 0 (t ).
Спектр :
1
S w
.
iw
(11)
(12)
Означення. Довжиною імпульса Δ t називається відрізок часу,
де зосереджена більша частина енергії імпульса, тобто:
t0
t
2
t0
t
2
Якщо t0=0, то:
f
2
t dt
t
2
0
f
2
t dt At ,
f 2 t dt f 2 t dt.
0
(13)

35. .

де
At f 2 t dt
(14)
- величина, яка пропорційна повній енергії імпульса ;
η – відносна доля повної енергії імпульса, яка спостерігається
за час Δ t ;
Означення. Ширина спектра визначається із:
w
0
Ф 2 w dw Ф 2 w dw Aw .
(15)
0
Зауважимо, що за теоремою Рейлі:
Aw At ,
(13)

36. .

37. Лекція 6. Зв’язок між спектрами та характеристикою лінійної системи

Нехай задана деяка лінійна система, яка описується
звичайним диференціальним рівнянням n-го порядку з
постійними коефіцієнтами:
(1)
Застосуємоn до обох частин
n 1 перетворення Фур’є :
d y
d y
dy
аn n аn 1 n 1 ... а1
а0 y x (t ).
dt
dt
dt
та , врахувавши формулу (22) лекції 2:
отримаємо:
(2)
S w де
f t- відповідні
exp( iwtспектри
) d t. для функцій x(t)
та y(t)
S( n ) w ( iw) n S w ,
[аn (iw)n аn 1 (iw) n 1 ... а1iw а0 ]S y S x ,
Sx , S y

38. .

Введемо позначення для полінома в дужках:
аn (iw) n аn 1 (iw) n 1 ... а1iw а0 Z ( w), (3)
Тоді рівняння (2) запишеться у вигляді:
Z ( w) S y S x ,
Звідси отримаємо:
Sx
Sy
,
Z ( w)
(4)
де застосуємо до лівої та правої частин обернене перетворення
Фур’є та отримаємо:
1
y t
2
Sx
exp(iwt ) d w.
Z ( w)
(5)
Ця формула дає розв'язок рівняння (1) методом інтеграла Фур’є.

39. .

Введемо наступне позначення :
1
K ( w)
,
Означення. Величина К(w) виражає відношення
Z ( wкомплексних
)
(6)
амплітуд на виході та на вході системи при синусоїдальному
режимі та називається комплексною частотною характеристикою.
Тоді рівняння (4) запишеться у вигляді (7) Тепер
розглянемо імпульсне збудження системи . Нехай на вході
( w) S x .
системи подається одиничний імпульс δ(t)S :y K(8)
При цьому на виході буде спостерігатися відгук системи на
такого роду дію, який позначимо:
x t (t ) .
(9)
Означення. Функція g(t) називається часовою характеристикою
системи.
y t g (t ) .

40. .

Для одиничного імпульса δ(t) спектр дорівнює
тоді в цьому випадку із (7) слідує:
S y K ( w).
Тоді маємо:
1
g t
2
а також
S x 1,
(10)
K (w) exp(iwt ) d w.
(11)
K w g (t ) exp( iwt ) d t.
(12)
Отже, комплексна частотна характеристика лінійної
системи є спектром часової характеристики системи.

41. Приклад

Нехай задано електричний ланцюжок, який складається
із опору R, індуктивності L та ємності С в послідовному зєднанні.
Диференціальне рівняння такого ланцюжка має вигляд:
(13)
di
1
L Ri
i d t e(t ).
Позначимоα:
dt
C
1
Тоді рівняння U
(16) прийме
вигляд:
i
d
t,
C
(14)
де
2
dU
dU
2
2
2
w
U
w
0
0 e(t ),
2
dt
dt
R
1
2
2 ; w0
.
L
LC

42. .

В даному випадку
w0 2
K ( w) 2
.
2
w0 w 2 iw
(15)
Часову характеристику системи отримаємо, як розв'язок
рівняння :
2
d g
dg
2
2
2
w0 g w0 (t ),
2
dt
dt
Звідки:
де
w0 2
g (t )
exp( t ) sin w1t ,
w1
w12 w0 2 2 .
Отже, вираз (16) є спектром функції (17).
(16)

43. Функції з обмеженим спектром

Теорема. Будь-яку функцію f(x), яка складається із частот від
0 до fс , можна передавати з будь-якою точністю за
допомогою чисел, які слідують один за одним через 1/ fс
секунд.
Доведення. Розкладемо функцію f(x) в ряд особливого
вигляду. Відомо, що функцію f(x) можна подати у вигляді
інтегралу Фур'є:
1
f t
S ( w)exp ( iwt ) dw ,
(1)
2
S w
f t exp( iwt ) d t ,
де
Оскільки функція f(x) - з обмеженим спектром . то
1
f t
2
бо S(w)=0 при w>wc.
wc
S (w)exp ( iwt ) dw ,
wc
(2)
(3)

44. .

Оскільки S(w) визначена на проміжку (-wc, wc), то її
можна розкласти в ряд Фур'є за частотами таким способом:
(4)
w
S w Dk exp (ik
k
wc
),
де 2wc грає роль періода за частотою.
Коефіцієнти ряда (4) визначаються за формулою:
1
Dk
2wc
Підставимо
1
f t
2
wc
w
S w exp( ik ) d w .
wc
wc
(5)
(4) в (3) і отримаємо:
wc
[
wc k
w
Dk exp (ik )]exp ( iwt ) dw ,
wc
(6)

45. .

або, змінивши порядок дій, маємо:
1
f t
2
k
wc
Dk
wc
exp iw(t k ) dw ,
wc
(6)
Звідки після інтегрування знаходимо:
1
f t
k
sin(t k
)
wc
Dk
,
(7)
(t k
)
wc
Порівняємо (5) і (7). Як видно,
Dk f ( k ) t f ( k t ),
wc
wc
(8)

46. .

Підставивши в (7) знайдене значення Dk із (8) і міняючи знаки
під знаком суми, маємо:
(9)
sin(t k t )
f t f (k t )
,
(t спектром
k t ) може бути
з обмеженим
Отже, функціяk f(x)
представлена рядом (9) , коефіцієнти якого є відліками
значень функції, які взято через інтервал:
(10)
1
t відліків
(теореми
.
теореми
wc 2 f c
Це – формулювання
Котельникова-Шеннона).

47. Лекція 7. Багатовимірні ряди та перетворення Фур’є

•1. Двовимірний ряд Фур’є отримуємо з
одновимірного
f x a0
(a
k
cos k x bk sin k x ),
(1)
k 1
коли величини ak , bk , f ( x) будемо вважати функціями , для
яких y ≠const, тобто:
f x, y a0 ( y )
[a ( y) cos k x b
k
k
( y ) sin k x],
(2)
де фукнкції ak ( y ), bk ( y ) , f ( x, y ) також можна розкласти в ряд
Фур’є по у, відповідно (1),тоді результуюча формула наступна.
k 1

48. .

Розклад функції в двовимірний ряд Фур’є
f x, y
k 0
[a
kn
cos k x cos n y bkn sin k x sin n y
n 0
ckn cos k x sin n y d kn sin k x cos n y ],
(3)
де величини akn , bkn , ckn , d kn - сonst.
f ( x, y ) по сферичним функціям
Розклад функції
f ,
n 0
k 0
[ An ( k ) cos k Bn ( k ) sin k ]Pn ( k ) (cos ),
(4)
де ε –довгота,
δ –( k доповнення
широти до 90 градусів,
(k )
)
(k )
An , Вn
P
величини
- сonst, а фукнкція n (cos ) - відповідний
поліном Лежандра першого роду степеня n і порядка k.

49. .

Тривимірне перетворення Фур’є
S (k x , k y , w)
f x, y, t exp [ i(k x k y wt )]dxdydt ,
x
y
(5)
1
f x, y , t
(2 )3
S (k , k , w)exp [ i(k x k y wt )]dk dk
x
y
x
y
x
y
dw .
де величини k x , k y - хвильові числа по двом просторовим
напрямкам x та у.
Часткові перетворення Фур’є
Часово-частотне:
S x, y , w
f x, y, t exp( iwt ) d t ,
(6)
Просторовохвильочислове: S k x , k y , t f x, y, t exp[ i (k x x k y y )]dxdy, (7)

50. Розклад функції в тривимірний ряд по сферичним функціям (спектральний розклад) .

Нехай ( x ), x R3, - однорідне ізотропне випадкове
поле в 3-D просторі. Це означає, що:
1) E ( x ) const (далі робимо припущення, що E ( x ) 0 )
2) E ( x ) ( y ) B( x y )
, де B( ) - кореляційна функція
випадкового поля ( x ) , де ρ - відстань між точками x та y R3.
Таке випадкове поле допускає спектральний розклад :
(r , , (8)
)
m
l
l
l
с
P
(cos
)
[
(
r
)cos
l
m ,l m
m ,1
m , 2 ( r )sin l ]
m 0 l 0
-
(r ) , k 1, 2
де r , , - сферичні координати (r- глибина),
послідовності випадкових процесів, які задовольняють умови:
1) ml , k (r ) 0 ; 2) ml , k ( r ) ml , k ( r ) ll mm kk bm ( r ) ,
(9)
де bm (r ) - спектральні коефіцієнти, а с - константи.
m ,l
l
m, k

51. .

Спектральні коефіцієнти можна обчислити так:
J m2 1 ( r )
bm (r ) (10)2
r
0
2
f ( )d , f ( )
sin B( )d .
0
де B( ) - кореляційна функція випадкового поля ( x ) , f(λ) – його
спектральна щільність, а Jk (x) – функція Бесселя першого роду
порядка k.
Модель поля в тривимірному просторі
N
m
l
l
l
N (r , , ) (11)
c
P
(cos
)
(
r
)cos
l
ml m
m , 2 ( r )sin l , N
m,1
m 0 l 0
Оцінка середньоквадратичного наближення поля моделлю:
(12)
5 r спектральної
2
де
моменти
( r , , ) N ( r , , ) 2 3 ,
2N
щільності. K
3 = 3 f d , K K (a) const.
3
0

52. Лекція 8. Розклад функції в двовимірний ряд (спектральний розклад) .

( x ),
xR2, - однорідне ізотропне випадкове поле в
Нехай
2-D просторі. Це означає, що:
1) E ( x ) const (далі робимо припущення, що E ( x ) )0
2) E ( x ) ( y ) B( x y )
, деB( ) - кореляційна функція
випадкового поля ( x ), де ρ - відстань між точками таx Ry2.
Таке випадкове поле допускає спектральний розклад :
(1)
(r , ) k 1k (r )cos k 2k (r )sin k ,
1, k 0;
k
де 2, k 0,
k 0
- полярні координати, l l
k (r ) J k ( r ) Z k (d ) , l 1, 2
r , випадкових процесів, які задовольняють
послідовності
умови:
0
(2)
l
l
l
l
k
1)-
k (r ) 0 ; коефіцієнти,
2) k (r ) kа (Jr )(x)
–l функція
k bm ( r )Бесселя
,
де
спектральні
першого
k
bm (r ) k.
роду порядка

53. .

Спектральні коефіцієнти можна обчислити так:
2
bk (r )
B (2 r sin )
cos 2 k d . k 1, 2,...
(3)
0
де B( )- кореляційна функція випадкового поля ( x ) .
Модель поля в двовимірному просторі
N
(r , ) k 1k (r ) cos k 2k ( r )sin k , N .
(4)
k 0
Оцінка середньоквадратичного наближення поля моделлю:
(r , ) N (r , )
2
1 1
2
r 1 r 2
N 2
K
(5)
i
=
де i 0 f d , i 1, 2; K K (a) const-.моменти спектральної
щільності випадкового поля ( x ) , яка визначається через B( ) :
f ( ) x J 0 ( x) B ( x)dx
0

54. Розклад функції на циліндрі з обмеженим спектром в двовимірний ряд .

Нехай дійснозначні випадкові поля (t, ), де t R=(- , ),
0,2 , з нульовим математичним сподіванням, періодичні з
періодом 2 за змінною та ізотропні за змінною Це означає, що:
де
(t , 1 ) функція
( s, 2 )випадкового
B(t , s, поля
),
1 2 (t, ).
- кореляційна
В(t,s, )
Таке випадкове поле допускає спектральний розклад :
(6)
1
(t , ) 0 (t ) k (t ) cos k k (t ) sin k ,
де послідовності
процесів, які задовольняють умови:
2 випадкових
k 1
(7)
де
r
bk(t,s)
спектральні
rкоефіцієнти.
(
t
)
(
s
)
k
r
k bk ( t , s),
(t ) ( s) b (t , s),
k
r
k
k

55. .

Спектральні коефіцієнти можна обчислити так:
1
bk (t , s) B (t , s, ) cos k d .
(3)
де В(t,s, ) - кореляційна функція випадкового поля (t, )
Модель поля в двовимірному просторі
n
sin c t
.
1 n M n
n
c .
N ,M (t , ) 0 k cos k k sin k
c k 1 c
c
n N 2
c t n
(4)
c
N
Оцінка середньоквадратичного наближення поля моделлю:
M
2
bm (0) K k
m М 1
де
M 2 (k 1)
,
k
M (k 1)
K k max B ( k ) (t s, 1 2 )
0 2
M ,
k 2
(5)
, k – індекс класу функцій Dk

56. Розклад функції на сфері з обмеженим спектром в двовимірний ряд .

Нехай дійснозначні випадкові поля (t, u), де t (- , ), u Sn, де
Sn – одинична сфера в n-вимірному евклідовому просторі Rn
Це означає, що:
(t , u ) ( s, ) B (t s, cos u, ).
де
B (t , s, cos u, ) - кореляційна функція випадкового поля (t, u),.
Таке випадкове поле допускає спектральний розклад :
(t , u )
m 0
h ( m ,n )
l
l
(
t
)
S
m m (u ),
l 1
(6)
l
l'
m' l '
випадкових
(
t
)
(
s
)
, s ,задовольняють умови:
де послідовності
процесів,
m
m'
m l bm t які
(7)
де bk(t,s) - спектральні коефіцієнти.

57. .

Спектральні коефіцієнти можна обчислити так:
n 2
n 3
2
n 1 1
2 2
2
bm (t , s )
C
n 2
2
m
B(t , s, x)C
m
( x) (1 x )
dx.
(1) 1
де В(t,s,x) - кореляційна функція випадкового поля (t,u)
Модель поля
r
sin
c
t
M h ( m,n )
N
r
c
N , M (t , 1 , , n 1 , ) S ml ( 1 , , n 1 , ) ml
.
c r
m 0 l 1
r N
c t
c
(8)
.
(9)
Оцінка середньоквадратичного наближення поля моделлю:
2
85576 p 4 1 p 2 (2 N 3) p M 1 (1 2 N ) p M 2
1
2
81675
(1 p)
де p (0,1).
(10)

58. Розклад однорідних за часом однорідних ізотропних випадкових полів за просторовими координатами в двовимірному просторі .

(t , , )
k
sin t
N
N ,M (t , r , ) =
k = N
k
t
k
m, j
,r
k
M
k
k
0,1 , r 2 m =1 m ,1 , r cos m m ,2 , r sin m ,
k
q
j m (k q )
E m,i
, r p, j
, r i p b m
,r
~
bm (t s, r )

59. .

Спектральні коефіцієнти можна обчислити так:
b m (t s, r ) =
e
i (t s )u
0
J m 2 (r ) (du , d ).
(13)
де (u , ) - просторово-часовим спектр випадкового поля (t , , )
Оцінка середньоквадратичного наближення поля моделлю:
2
2 1
8
2
E (t , r , ) N ,M (t , r , )
0 ,
r 1 r 2 2
M 2
(2 N 1)
де
k =
k
du, d ,
0
(14)

60. Лекція 8. Способи обчислення спектрів

• 1. Прямий спосіб
• 2. Непрямий спосіб
• 3. Швидке перетворення Фур’є
1. Прямий спосіб обчислення спектрів (метод періодограм)
Коефіцієнти Фур’є:
1 N
2k
a w a k f (v) cos (
v),
(1)
N k 1
N
1 N
2k
b w b k f (v) sin (
v),
(2)
N k 1
N
амплітудний спектр:
2
2
S ( w)(3) a ( w) b ( w)
1/2
.

61. .

енергетичний спектр:
2
(4)
S ( w) a 2 ( w) b 2 ( w).
фазовий спектр:
(5)
tgФ( w) b( w) / а( w).
Періодограма:
(6)
S ( w)
T
2
2
2
a ( w) b ( w)
.
T
де Т – інтервал спостереження .

62. .

2. Непрямий спосіб обчислення спектрів
Кореляційна функція:
C11
1
N
N
f (t ) f (t ) , 0,1, 2,..., m.
(7)
k 1
енергетичний спектр:
E11 w (8)
2 C11 cos w d .
0
енергетичний спектр в дискретній формі:
m 1
(9)
1
l
E11 l [C11 0 2 C11 cos ( ) C11 m cos l ],
m
m
1

63. .

Поправки за апаратуру:
E (l ) I (l ) EI (l ).
(10)
Коефіцієнти згладжування Хемінга-Тьюкі та Ханна:
0,54
0, 46
EI 0
EI 0
EI 1 ,
0,50
0,50
0, 23
0,54
EI l
EI l 1
EI l
0, 25
0,50
(11)
0, 23
EI l 1 ,1 l m 1,
0, 25
0, 46
0,54
EI m
EI m 1
EI m ,
0,50
0,50

64. Лекція 9. Спосіб швидкого перетворення Фур’є

ШПФ більш ефективний, ніж попередні способи обчислення
спектрів . Він виник в середині 1960 р.
Нехай задано дискретний ряд спостережень f(t), t=1,2,…,N,
де N – парне число. Ділимо цей рядна дві частини: відліки з
парними індексами
причому,
y xі непарними,
x , x ,...,
x , t=1, 2, …, N/2.
t
(1)
2t 1
1
3
N 1
zt x2t x2 , x4 ,..., xN .
Запишемо дискретне перетворення Фур’є цих трьох рядів:
(N )
X
(2) n
( N /2)
Y
(3) n
1 N
2n
xt exp ( i
t ),
N t 1
N
2 N /2
4n
yt exp ( i
t ),
N t 1
N

65. .

Z
( N /2)
n
2
N
N /2
t 1
4n
zt exp ( i
t ).
N
(4)
Перетворення Фур’є цих трьох рядів теж пов'язані між
собою:
N /2
1
2n
2n
(N )
X n [ yt exp ( i
)(2t 1) zt exp ( i
)2t ]
N t 1
N
N
2n 1 N /2
4n
1 N /2
4n
exp (i
) yt exp ( i
)t zt exp ( i
)t
N N t 1
N
N t 1
N
1
2n ( N /2) 1 ( N /2)
(5)
exp (i
)Yn Z n .
2
N
2
Замінивши n на n+N/2, знаходимо:
( N /2)
n N /2
Y
( N /2)
n
Y
,Z
( N /2)
n N /2
Z
( N /2)
n
,
(6)

66. .

4n
4n
4n
t
(n N / 2)t
t 2 t ,
N
N
N
(7)
що у випадку цілого t складає показникову функцію без змін.
Внаслідок цього отримаємо:
1
2
1 ( N /2)
( N /2)
X
exp (i )(n N / 2)Yn N /2 Z n N /2
2
N
2
1
2n ( N /2) 1 ( N /2)
exp (i
)Yn Z n .
2
N
2
(N )
n N /2
(8)
1
2nформули
( N /2) (5)1та (8),
( N ) Перепишемо
( N /2)які є основними в ШПФ:
Xn
exp (i
)Yn
Z n , n 0,1, 2,...,( N / 2) 1,
2
N
2
1
2n ( N /2) 1 ( N /2)
(N )
X n N /2 exp (i
)Yn Z n ,
2
N
2
(9)
n N / 2 N / 2, N / 2 1,..., N 1.

67. .

Отже, застосовуючи ШПФ , необхідно вибирати дискретний
ряд спостережень f(t), t=1,2,…,N, де N 2 k , тобто:
k=1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
N=2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096
На практиці N
та k визначають так:
1) Вибираємо повний інтервал аналіза: вибірка із випадкового
процеса;
2) Вибираємо інтервал дискретизації із урахуванням явища
маскування частот;
3) В загальному випадку відношення інтервала аналіза до
інтервала дискретизації може не бути рівним
k , тоді - або
2
добавити об'єм вибірки, або доповнити нулями процес.

68. Лекція 10. Спектри Уолша

• Функції Уолша:
w j ( x) 0, x 0, x 1,
w0 ( x) 1, 0 x 1,
(1)
j
w2 j ( x) w j (2 x) ( 1) w j (2( x 1/ 2)),
w2 j 1 ( x) w j (2 x) ( 1)
j 0,1, 2,...
j 1
w j (2( x 1/ 2)),

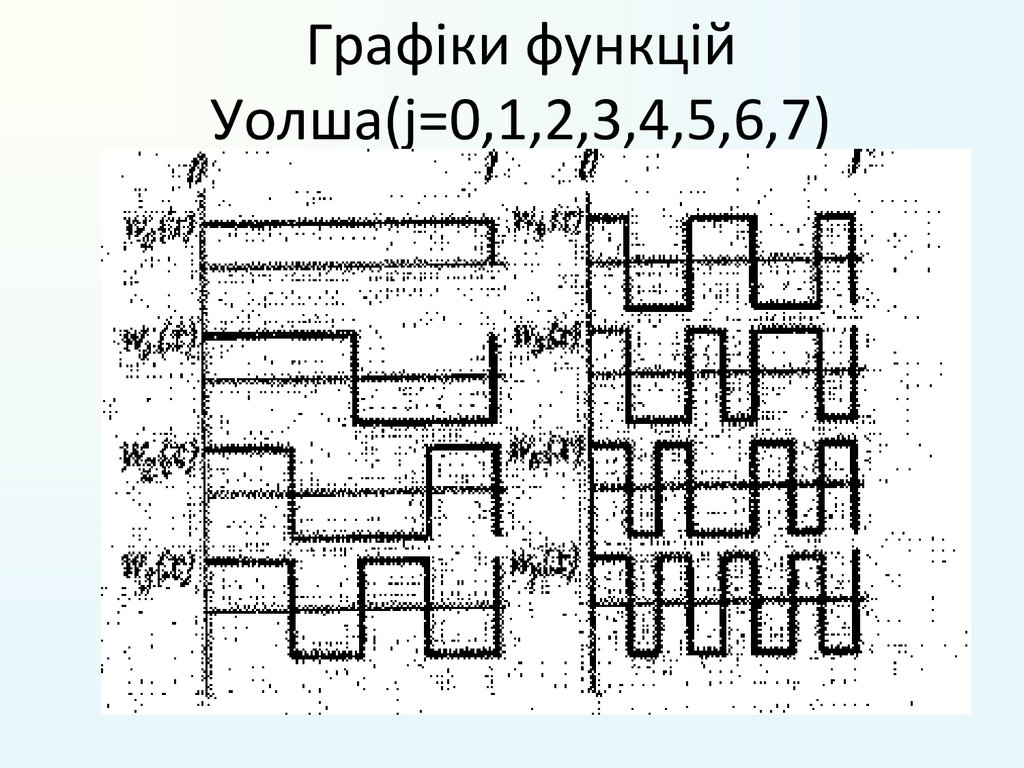
69. Графіки функцій Уолша(j=0,1,2,3,4,5,6,7)

70. Властивості функцій Уолша

• 1) Індекс j дорівнює числу 0-лів в інтервалі
0<x<1 і називається частотою слідування.
2) функції Уолша з парною частотою
симетричні відносно x=1/2
w2 j 1 ( x) sal ( j , x ),
w2 j ( x) cal ( (2)
j , x).
3)
функції Уолша є ортонормована послідовність
функцій
1
1, i (3)j;
w ( x) w ( x) dx
0
i
j
0, i j.

71. .

Формули прямого та оберненого дискретних
скінченних перетворень Уолша
1
S ( j)
N
N 1
f ( xi ) w j ( xi ),
i 0
N 1
f ( xi ) S ( j ) w j ( xi ).
j 0
(4)
(5)

72. .

Формули прямого та оберненого двовимірних
дискретних скінченних перетворень Уолша
1
S (k , l ) 2
N
N 1 N 1
i 0
j 0
N 1 N 1
f ( xi , y j )
l 0
f ( xi , y j ) wk ( xi ) wl ( y j ),
k 0
(6)
S (k , l ) wk ( xi ) wl ( y j ).
(7)