Похожие презентации:
Учет погрешностей при вычислениях. Лекция 1
1. АНИМАЦИОННЫЙ БЛОКБАСТЕР ПО ДИСЦИПЛИНЕ «ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА»
Автор сценария, режиссер, продюсер и т.д.,и т.п.: к.т.н., доцент Горбунов Д.А.
Сопродюссер: не менее важный доцент
Комиссарова Е.М.
Цитата: «Если Вы пришли в магазин и
просите взвесить полкило колбасы, то это не
значит, что Вам взвесят ровно 500 грамм».
Так
возникли
методы
приближенных
вычислений, а также погрешности измерений.
© Казань, 2007
2. ЛЕКЦИЯ 1
УЧЕТ ПОГРЕШНОСТЕЙ ПРИВЫЧИСЛЕНИЯХ
3. КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ
1. Погрешности задачи.2. Погрешность метода.
3. Остаточная погрешность.
4. Начальная погрешность.
5. Погрешность округления.
6. Погрешность действий.
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Определение. Приближенным числом a называется число, незначительно
отличающееся от точного числа A .
Если
a A
, то a
: приближенное число с избытком.
Если
a A
, то a
: приближенное число с недостатком.
Определение. Погрешность a
приближенного числа a : a A a .
Определение. Абсолютная погрешность приближенного числа a : A a a .
4. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Определение. Относительная погрешность приближенного числаa
a
: A A .
Определение. Предельная абсолютная погрешность a : A a a .
Определение. Предельная относительная погрешность
a
:
a
.
Определение. Значащей цифрой приближенного числа называется всякая цифра,
отличная от нуля, и нуль, если он находится между значащими цифрами или
является представителем сохраненного десятичного разряда.
Определение (первое определение верной цифры). Цифра называется
верной цифрой приближенной величины, если абсолютная погрешность
приближенной величины не превосходит единицы десятичного разряда,
выражаемого этой цифры.
Определение (второе определение верной цифры). Если абсолютная
погрешность приближенного числа
разряда, выражаемого
приближенного числа a
n
a
не превышает половины единицы
-й значащей цифрой, то
являются верными.
n
первые значащие цифры
5. ОКРУГЛЕНИЕ ЧИСЕЛ
Чтобы округлить приближенное число a довсе цифры, стоящие справа от
n значащих цифр, отбрасывают
n -й значащей цифры, или заменяют их нулями.
При этом, если первая из отброшенных цифр:
1. Меньше 5, то оставшиеся десятичные знаки сохраняются без изменения.
2. Больше 5, то к последней оставшейся цифре прибавляется единица.
3. Равна 5 и среди остальных отброшенных есть неравные нулю, то последняя
оставшаяся цифра увеличивается на единицу.
4. Равна 5 и все остальные отброшенные цифры равны нулю, то последняя
оставшаяся цифра остается неизменной, если она четная, и увеличивается на
единицу, если она нечетная (правило четной цифры).
ПОГРЕШНОСТЬ АЛГЕБРАИЧЕСКОЙ СУММЫ
Теорема.
Абсолютная
погрешность
алгебраической
суммы
нескольких
приближенных чисел не превышает суммы абсолютных погрешностей этих
чисел.
Следствие. Предельная абсолютная погрешность алгебраической суммы:
u a1 a 2 ... a n
6. ПОГРЕШНОСТЬ ПРОИЗВЕДЕНИЯ
Теорема. Относительная погрешность произведения нескольких приближенныхчисел, отличных от нуля, не превышает суммы относительных погрешностей
этих чисел.
Следствие 1. Предельная относительная погрешность произведения:
u a1 a 2 ... a n
Следствие 2.
u a
u k a
ПОГРЕШНОСТЬ ЧАСТНОГО
Теорема. Относительная погрешность частного не
относительных погрешностей делимого и делителя, т.е.:
превышает
суммы
1 2
ПОГРЕШНОСТЬ СТЕПЕНИ
Теорема. Предельная относительная погрешность
k
-й степени числа x
в
k
раз больше предельной относительной погрешности самого числа:
u k x
ПОГРЕШНОСТЬ КОРНЯ
Теорема. Предельная относительная погрешность корня k -й степени числа x
в k
раз больше предельной относительной погрешности самого числа:
1
u x
k
7. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие основные причины возникновения ошибок существуют?2. Какие погрешности называются погрешностями задачи?
3. Что называется погрешностью метода?
4. Что называется остаточной погрешностью?
5. Что называется начальной погрешностью?
6. С чем связана погрешность округления?
7. Когда возникает погрешность действий?
8. Какие погрешности изучаются в курсе «Численные методы»?
9. Что называется приближенным числом?
10. Что называется погрешностью (ошибкой) приближенного числа?
11. Что называется абсолютной погрешностью приближенного числа?
12. Что называется относительной погрешностью приближенного числа?
13. Что называется предельной абсолютной погрешностью приближенного числа?
14. Что называется предельной относительной погрешностью приближенного числа?
15. Что называется значащей цифрой приближенного числа?
16. Какая цифра называется верной цифрой приближенного числа?
17. Сформулируйте правило округления чисел.
18. Что берется за предельную абсолютную погрешность алгебраической суммы приближенных чисел?
19. Чему равна предельная относительная погрешность приближенных чисел?
20. Чему равна предельная относительная погрешность частного приближенных чисел?
21. Чему равна предельная относительная погрешность корня k-й степени приближенного числа?
22. Чему равна предельная относительная погрешность k-й степени приближенного числа?
8. ЛЕКЦИЯ 2
ОСНОВНЫЕ ЭТАПЫ РЕШЕНИЯНЕЛИНЕЙНЫХ УРАВНЕНИЙ
9. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Определение 1. Нелинейными уравнениями называются уравнения вида:где
f x 0
f x это:
1
1) нелинейная алгебраическая функция (полином) вида:
an x n an 1x n 1 a1x a0 ;
2)
трансцендентная
функция
(тригонометрические,
логарифмические,
экспоненциальные, показательные и другие функции);
3) комбинирование полиномов и трансцендентных функций.
Определение 2. Решением нелинейного уравнения (1) является такое значение
x* , при подстановке которого в исходное уравнение последнее обращается в
тождество, т.е.
f x* 0.
Определение 3. Приближенным решением нелинейного уравнения (1) является
такое значение x** , при подстановке которого в исходное уравнение последнее
выполняется с заданной точностью
малая положительная величина.
**
, т.е. f x , где
- достаточно
10. ОСНОВНЫЕ ЭТАПЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
НЕЛИНЕЙНЫЕУРАВНЕНИЯ
Этап 1. Отделение корней
нелинейных уравнений
На
данном
этапе
для
поиска
приближенного
значения
единственного
корня
на
отрезке
необходимо
применить
любой из
нижеперечисленных методов.
Этап 2. Уточнение корней
нелинейных уравнений
Графический метод
Метод деления
отрезка пополам
Аналитический метод
Метод простых итераций
На данном этапе необходимо исследовать нелинейное
уравнение (1) и выяснить, имеются корни или нет, и,
если
имеются,
то
определить
их
количество
(графический метод). Затем необходимо выявить
интервалы, в каждом из которых должен находиться
единственный корень (аналитический метод).
Метод Ньютона
(метод касательных)
Модифицированный метод
Ньютона
11. ГРАФИЧЕСКИЙ МЕТОД
Если график функции y f x имеет простойy
y f x
аналитический вид, то его можно
непосредственно построить и определить точки
его пересечения с осью OX. Эти точки и будут
являться приближенными значениями корней
нелинейного уравнения (1).
0
Если график функции y f x имеет сложный
аналитический вид, то его можно представить в
x
y
y 2 x .
виде разности двух более простых функций:
f x 1 x 2 x 0. Тогда 1 x 2 x .
(1)
Таким образом, задача решения нелинейного
y 1 x
уравнения (1) сводится к поиску точек пересечения
графиков функций y 1 x и
y 2 x . Эти точки и
будут являться приближенными значениями
корней нелинейного уравнения (1).
0
x
12. ПРИМЕРЫ
Пример 1. Дано нелинейное уравнение:f x e x x 0.
Разбиваем исходный график на два более простых:
e x x.
8
6
4
y=exp(-x)
2
y=x
0
Вывод: исходное уравнение имеет единственный корень.
-2
Пример 2. Дано нелинейное уравнение:
f x e x x 0.
10
Разбиваем исходный график на два более простых:
e x x.
4
Вывод: исходное уравнение корней не имеет.
-2
-2
-1
0
1
2
3
4
5
-4
8
6
y=exp(-x)
2
y=-x
0
-2
-1
0
1
2
3
4
5
-4
-6
Пример 3. Дано нелинейное уравнение:
f x sin 2x x 0.
2
1,5
1
0,5
Разбиваем исходный график на два более простых:
sin 2x x.
-0,5 -1,5 -1,1 -0,7 -0,3 0,1 0,5 0,9 1,3
Вывод: исходное уравнение имеет три корня.
-1,5
0
-1
-2
y=sin(2x)
y=x
13. АНАЛИТИЧЕСКИЙ МЕТОД
Данный метод основывается на следующих теоремах:Теорема 1. Если функция f x непрерывна на отрезке a, b и на концах отрезка
меняет знак ( f a f b 0 ), то на отрезке содержится хотя бы один корень.
Теорема 2. Если функция f x непрерывна на отрезке a, b , на концах отрезка меняет
знак ( f a f b 0 ), а производная f x на отрезке знак сохраняет, то на отрезке
содержится единственный корень.
Теорема 3. Если функция f x является полиномом n степени и на концах отрезка
меняет знак ( f a f b 0 ), то на отрезке содержится нечетное число корней (если
производная f x на отрезке знак сохраняет, то на отрезке содержится единственный
корень). Если функция на отрезке знак сохраняет, то на отрезке содержится четное число
корней или корней нет.
14. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ АНАЛИТИЧЕСКОГО МЕТОДА
y f x имеет на отрезке a, b два пересечения с осью OXФункция
1. Определяются точки, в которых производная f x 0 (точки
2. Выделяются интервалы монотонности функции:
c, d , e ).
a, c , c, d , d , e , e, b .
3. Из этих интервалов выбираются те, на которых функция меняет знак:
4. На интервалах
1 , 2 .
a, c , e, b .
a, c , e, b содержится по одному корню, соответственно 1, 2 , и для
нахождения их приближенного значения можно использовать методы уточнения корней.
y
0 a
y f x
1
c
d
e
2
b
x
15. МЕТОД ДЕЛЕНИЯ ОТРЕЗКА ПОПОЛАМ
Пусть нелинейное уравнение (1) имеет на отрезкеa, b единственный вещественный корень
a,b . Требуется найти его с заданной точностью .
Разбиваем отрезок
a, b пополам точкой x0 (нулевое или начальное приближение (итерация))
и из двух полученных отрезков
т.е.
a, x0 , x0 , b выбираем тот, на котором функция y f x меняет знак,
a, x0 . Разбиваем его пополам точкой
x1 (первое приближение) и получаем отрезок a, x1 .
И т.д. до тех пор, пока модуль разности между последующим приближением
приближением
x1 (т.е. длина отрезка
x2
и предыдущим
x2 , x1 ) не будет превышать заданной точности , т.е.
x2 x1 .
Тогда в качестве приближенного значения корня выбирается последнее приближение
x2 .
x2 , т.е.
16. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ МЕТОДА ДЕЛЕНИЯ ОТРЕЗКА ПОПОЛАМ
yy f x
0
a
x2
x1
x0
b
x
17. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какое уравнение называется нелинейным?2. Что называется решением нелинейного уравнения?
3. Когда возникает задача приближенного решения нелинейных уравнений?
4. Что называется приближенным решением нелинейного уравнения?
5. Назовите основные этапы решения нелинейных уравнений.
6. В чем состоит этап отделения корней нелинейных уравнений?
7. В чем состоит этап уточнения корней нелинейных уравнений?
8. В чем состоит графический метод?
9. В чем состоит аналитический метод?
10. Сформулируйте теорему о существовании хотя бы одного корня нелинейного уравнения
на отрезке.
11. Сформулируйте теорему о существовании единственного корня нелинейного уравнения
на отрезке.
12. В чем состоит метод половинного деления?
18. ЛЕКЦИЯ 3
УТОЧНЕНИЕ КОРНЕЙ НЕЛИНЕЙНЫХУРАВНЕНИЙ
(метод простых итераций)
19. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ ДЛЯ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Пусть нелинейное уравнение (1) имеет на отрезке a, b единственный вещественный кореньa,b . Требуется найти его с заданными точностями , .
2
xn 1 xn , n 0,1,2... 3
1. От нелинейного уравнения (1) переходим к виду:
2. Итерационный процесс:
x x .
3. Теорема 4 (теорема о достаточных условиях сходимости итерационного процесса (3)). Если
функция x определена и дифференцируема на отрезке
a,b , все ее значения принадлежат отрезку
1, x a, b , 4 то итерационный процесс (3) сходится к
и выполняется условие: x
единственному корню нелинейного уравнения (1) независимо от выбора начального приближения
4. Начальное приближение выбирается произвольно из отрезка.
5. Сходящийся итерационный процесс:
xn 1 cf xn xn , n 0,1,2...,
x0 .
5 где значение
неизвестной постоянной
а) если
б) если
c выбирается из соответствующего двустороннего неравенства:
f x 0 x a, b , то 2 f x c 0.
f x 0 x a, b , то 0 c 2 f x .
6. Условия окончания итерационных процессов (3) и (5):
xn 1 xn & f xn 1 .
7. Достоинства метода простых итераций:
а) метод является универсальным, самоисправляющимся и простым для реализации на ЭВМ;
б) метод позволяет находить решение уравнения (1) при любом начальном приближении из отрезка.
8. Недостатки метода простых итераций:
а) если начальное приближение выбрано достаточно далеко от корня, то число итераций возрастает
(метод обладает медленной скоростью сходимости);
б) метод является трудоемким.
20. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ МЕТОДА ПРОСТЫХ ИТЕРАЦИЙ (случай сходящегося итерационного процесса, «лестница»)
yy x
y x
x0
x1
0a
x2
x1
x0
b
x
21. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ МЕТОДА ПРОСТЫХ ИТЕРАЦИЙ (случай сходящегося итерационного процесса, «спираль»)
yy x
x1
x0
0 a x
1
y x
x2 x0 b
x
22. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ МЕТОДА ПРОСТЫХ ИТЕРАЦИЙ (случай расходящегося итерационного процесса)
y xy
y x
x1
x0
0
a
x0
x1
b
x2
x
23. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Сформулируйте постановку задачи метода простых итераций.2. Сформулируйте основную идею метода простых итераций.
3. Запишите итерационную формулу метода простых итераций.
4. Как выбирается начальное приближение в методе простых итераций?
5. Приведите геометрическую интерпретацию метода простых итераций (случай
«лестница»).
6. Приведите геометрическую интерпретацию метода простых итераций (случай
«спираль»).
7. Приведите геометрическую интерпретацию метода простых итераций в случае
расходящегося итерационного процесса.
8. Сформулируйте теорему о достаточных условиях сходимости метода простых итераций.
9. Покажите процесс приведения нелинейного уравнения к виду, допускающему
сходящиеся итерации.
10. Запишите условия окончания итерационного процесса по методу простых итераций.
11. Почему условия окончания итерационного процесса по методу простых итераций
должны выполняться одновременно?
12. Сформулируйте достоинства и недостатки метода простых итераций.
24. ЛЕКЦИЯ 4
УТОЧНЕНИЕ КОРНЕЙ НЕЛИНЕЙНЫХУРАВНЕНИЙ
(метод Ньютона и его модификация)
25. МЕТОД НЬЮТОНА (МЕТОД КАСАТЕЛЬНЫХ) ДЛЯ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Пусть нелинейное уравнение (1) имеет на отрезкеa, b единственный вещественный корень
a,b . При этом, производные f x , f x не равны нулю и сохраняют определенные знаки на
отрезке. Требуется найти его с заданными точностями , .
1. Итерационный процесс:
xn 1 xn
f xn
, n 0,1,2...
f xn
6
2. В качестве начального приближения выбирается один из концов отрезка, в котором выполняется
7
3. Теорема 4. Если f a f b 0 и производные f x , f x не равны нулю и сохраняют
достаточное условие сходимости вида:
f x f x 0
определенные знаки на отрезке, то исходя из начального приближения, удовлетворяющему условию
(7), по формуле (6), можно уточнить корень уравнения (1) с любой степенью точности.
xn 1 xn & f xn 1 .
4. Условия окончания итерационного процесса (6):
5. Достоинства метода Ньютона:
а) метод обладает высокой скоростью сходимости, близкой к квадратичной;
б) метод имеет единую итерационную формулу.
6. Недостатки метода Ньютона:
а) не при любом начальном приближении метод сходится, а лишь при том, в котором выполняется
условие (7) и условие f x0 0.
б) если
f xn 0, то
n
в) если
f xn ,
n
то
f xn
.
f xn n
f xn
0.
f xn n
26. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ МЕТОДА НЬЮТОНА
yy f x
f x0
f x1
f x2
0a
x2
x1
x0 b
x
27. МОДИФИЦИРОВАННЫЙ МЕТОД НЬЮТОНА ДЛЯ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Пусть нелинейное уравнение (1) имеет на отрезкеa, b единственный вещественный корень
a,b . При этом, производные f x , f x не равны нулю и сохраняют определенные знаки на
отрезке. Требуется найти его с заданными точностями , .
1. Предполагается, что производная
f xn
приближения.
2. Итерационный процесс:
xn 1 xn
мало изменяется в окрестности начального
f xn
, n 0,1,2...
f x0
8
3. В качестве начального приближения выбирается один из концов отрезка, в котором выполняется
достаточное условие сходимости вида:
f x f x 0
4. Условия окончания итерационного процесса (8):
7
xn 1 xn & f xn 1 .
5. В отличие от метода Ньютона, в модифицированном методе касательные заменяются на
прямые, параллельные касательной, проведенной из точки
x0 , f x0 .
28. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ МОДИФИЦИРОВАННОГО МЕТОДА НЬЮТОНА
yy f x
f x0
f x1
f x2
0a
x2
x1
x0 b
x
29. ПРИМЕР 4. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.
Постановка задачи.1. Доказать графическим и аналитическим методами существование
единственного корня нелинейного уравнения
f x e x x 0
1
на отрезке
x a,b .
2
2. Построить рабочие формулы по методу простых итераций, методу Ньютона
и модифицированному методу Ньютона, реализующие процесс поиска корня
нелинейного уравнения (1) на отрезке.
30. ПРИМЕР 4. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.
Прежде, чем приступить к построению итерационных формул, нужно убедиться,что нелинейное уравнение (1) имеет на отрезке (2) имеет единственный корень.
1. Графический метод.
2. Аналитический метод.
Представим исходное уравнение в виде:
а) Функция на концах отрезка должна менять знак:
e x.
x
f 1 0, f 0 0;
б) Производная на отрезке должна сохранять знак:
3
2,5
f x e x x.
2
1,5
1
y=exp(x)
0,5
y=-x
f 1 0, f 0 0.
0
-0,5
-1
-0,5
0
0,5
1
-1
-1,5
Вывод: нелинейное уравнение (1) имеет на отрезке (2) единственный корень.
31. ПРИМЕР 4. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.
3. Метод простых итераций.а) Так как
то
f x 0 x 1,0 ,
x0 1 : e x0 x0 e x0 0;
x0 0 : e x0 x0 e x0 0;
2
c 0;
ex 1
б) Выбираем любую точку из отрезка:
x 0 : c 0.5 ;
в) Итерационная формула:
f x e x .
xn 1 xn 0.5 e xn xn , n 0,1,...
г) Выбор начального приближения:
x0 1,0 .
4. Метод Ньютона.
а) Выбор начального приближения:
x0 a b : f x0 f x0 0.
б) Итерационная формула:
e xn xn
xn 1 xn xn
, n 0,1,...
e 1
5. Модифицированный метод Ньютона.
а) Выбор начального приближения:
x0 0;
б) Итерационная формула:
e xn xn
xn 1 xn x0
, n 0,1,...
e 1
32. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Сформулируйте постановку задачи метода Ньютона.2. Запишите рабочую формулу метода Ньютона.
3. В чем состоит геометрический смысл метода Ньютона.
4. Сформулируйте теорему о сходимости метода Ньютона.
5. Запишите достаточное условие сходимости метода Ньютона.
6. Как выбирается начальное приближение в методе Ньютона?
7. В каком случае метод Ньютона является частным случаем метода простых итераций?
8. Сформулируйте достоинства и недостатки метода Ньютона?
9. Сформулируйте постановку задачи модифицированного метода Ньютона.
10. Запишите рабочую формулу модифицированного метода Ньютона.
11. В чем состоит геометрический смысл модифицированного метода Ньютона.
12. Запишите условия окончания метода Ньютона и его модификации.
13. На какие схемы делятся итерационные методы решения нелинейных уравнений?
14. В чем состоят дискретные схемы решения нелинейных уравнений?
15. В чем состоят непрерывные схемы решения нелинейных уравнений?
16. В чем состоит принципиальное отличие непрерывных схем решения нелинейных
уравнений от дискретных?
33. ЛЕКЦИЯ 5
ИТЕРАЦИОННЫЕ МЕТОДЫРЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ
УРАВНЕНИЙ
34. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Определение 4. Системами нелинейных уравнений (СНУ) называются системывида:
f1 x1 , x2 xn 0,
f x , x x 0,
2 1 2
n
f n x1 , x2 xn 0,
если хотя бы одна из функций
fi
(9)
нелинейна. Здесь
неизвестных переменных, а система является порядка
x1 , x2 ,..., xn вектор
n n.
n
Пусть функции f i определены в областях i . Тогда область i
i 1
и будет являться областью, где находится решение системы.
35. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ ДЛЯ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Пусть дана СНУ (9). Требуется решить ее с заданной точностьюx1 1 x1 , , xn
10
x x , , x
n 1
n
n
1. Приведение системы (9) к эквивалентному виду:
2. Итерационный процесс:
.
x1 k 1 1 x1 k , , xn k
11
x k 1 x k , , x k , k 0,1,...
n 1
n
n
3. Выбор начального приближения: x
0
x1 0 , , xn 0 .
4. Достаточные условия сходимости итерационного процесса (11):
i
1, j 1, n
i 1 x j
n
или
n
i
j 1
j
x 1, i 1, n.
5. Условия окончания итерационного процесса (11):
x k 1 x k .
6. Достоинства метода простых итераций: метод является универсальным, самоисправляющимся
и простым для реализации на ЭВМ.
7. Недостатки метода простых итераций:
а) метод обладает медленной скоростью сходимости;
б) метод является трудоемким
n .
2
36. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ ДЛЯ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ ВТОРОГО ПОРЯДКА
Пусть дана СНУ второго порядка:f1 x, y 0,
f 2 x, y 0.
12
Требуется привести ее к виду, допускающему сходящиеся итерации:
x 1 x, y ,
y 2 x, y .
13
1. Достаточные условия сходимости итерационного процесса (13):
1 2
x x 1,
1 2 1.
y
y
2. СЛАУ для определения неизвестных коэффициентов:
3. Сходящийся итерационный процесс:
x k 1 1 x k , y k x k f1 x k , y k f 2 x k , y k ,
f1
f 2
1 x x 0,
f1 f 2 0,
x
x
f
f
1 2 0,
y
y
f
f
1 1 2 0.
y
y
y k 1 2 x k , y k y k f1 x k , y k f 2 x k , y k , k 0,1,...
4. Выбор начального приближения:
14
15
x , y .
0
0
5. Условия окончания итерационного процесса (15):
x k 1 x k & y k 1 y k .
37. МЕТОД НЬЮТОНА И ЕГО МОДИФИКАЦИЯ ДЛЯ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Пусть дана СНУ (9). При этом, функцииf i определены и дифференцируемы в области
и имеют первую производную по каждому из аргументов. Требуется решить систему с заданной
точностью
.
1. Итерационная формула метода Ньютона:
где
f1
x1
k
J x ...
f n
x
1
f1
x2
...
f n
x2
x k 1 x k J 1 x k f x k , k 0,1,...
f1
xn
... ... .
f n
...
xn
...
2. Итерационная формула модифицированного метода Ньютона:
x k 1 x k J 1 x 0 f x k , k 0,1,...
где
f1
x1
0
J x ...
f n
x
1
f1
x2
...
f n
x2
17
f1
xn
... ... .
f n
...
xn
...
3. Выбор начального приближения: x
0
x1 0 , , xn 0 .
4. Условия окончания итерационных процессов (16) и 17):
x k 1 x k .
16
38. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие системы называются нелинейными?2. Запишите постановку задачи по методу простых итераций.
3. Запишите итерационные формулы по методу простых итераций.
4. Как и из какой области выбирается начальное приближения для метода простых
итераций?
5. Запишите достаточные условия сходимости метода простых итераций.
6. Приведите один из способов приведения системы нелинейных уравнений второго
порядка к виду, допускающему сходящиеся итерации.
7. Запишите условия окончания итерационного процесса по методу простых итераций.
8. Приведите достоинства и недостатки метода простых итераций.
9. Запишите постановку задачи по методу Ньютона.
10. Запишите рабочую формулу метода Ньютона.
11. Запишите рабочую формулу модифицированного метода Ньютона.
12. Запишите условия окончания итерационного процесса по методу Ньютона и его
модификации.
39. ЛЕКЦИЯ 6
ИТЕРАЦИОННЫЕ МЕТОДЫРЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
40. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Определение 5. Системами линейных алгебраических уравнений (СЛАУ)называются системы вида:
или в матричном виде:
где
a11 a12
a22
a
A 21
... ...
a
n1 an 2
... a1n
... a2 n
,
... ...
... ann
a11x1 a12 x2 a1n xn
a x a x a x
21 1
22 2
2n n
...
...
...
an1 x1 an 2 x2 ann xn
Ax B,
x1
x
x 2 ,
...
x
n
b1 ,
b2 ,
...
bn ,
18
19
b1
b
B 2 .
...
b
n
Для решения СЛАУ вида (18) или (19) существуют точные методы (метод
Гаусса, метод Крамера, с помощью обратной матрицы и т.д.). Однако, при
большом числе неизвестных применение точных методов решения затруднено.
В этом случае целесообразней использовать приближенные (численные)
методы.
41. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ ДЛЯ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Пусть дана СЛАУ (18) или в матричном виде (19). Требуется решить ее с заданной точностьюПредполагается, что
aii 0, i 1, n (в случае равенства нулю одного или нескольких диагональных
коэффициентов с помощью перестановки уравнений или других эквивалентных преобразований
можно добиться, чтобы они были отличны от нуля).
x1 1 12 x2 13x3 ... 1n xn ,
x x x ... x ,
2
2
21 1
23 3
2n n
.............................................................
xn n n1x1 n 2 x2 ... nn 1xn 1.
1. Приведение системы (18) к эквивалентному виду:
или в матричном виде:
x x,
20
11 12
aij
bi
21 22
где: i , ij , i, j 1, n; ii 0, i 1, n;
aii
aii
...
...
n1 n 2
... 1n
1
... 2 n
2
,
... .
... ...
... nn
n
2. Итерационный процесс:
x k 1 x k , k 0,1,...
3. Выбор начального приближения:
x 0 .
21
.
42. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ ДЛЯ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
4. Теорема 5 (теорема о достаточных условиях сходимости итерационного процесса (21)): еслидля приведенной системы (20) выполнено одно из двух неравенств:
n
ij 1, j 1, n
n
или
i 1
1, i 1, n,
j 1
ij
то итерационный процесс (21) сходится к единственному решению этой системы независимо от выбора
начального приближения.
Следствие: для исходной системы (18) итерационный процесс (21) сходится, если выполнены
неравенства:
n
aii aij , i 1, n (т.е. модули диагональных коэффициентов больше суммы
i j 1
модулей всех остальных коэффициентов, не считая столбца свободных членов).
5. Условия окончания итерационного процесса (11):
x k 1 x k .
6. Достоинства метода простых итераций: метод является универсальным, самоисправляющимся
и простым для реализации на ЭВМ.
7. Недостатки метода простых итераций:
а) метод обладает медленной скоростью сходимости;
б) метод является трудоемким.
43. МЕТОД ЗЕЙДЕЛЯ
Пусть дана СЛАУ (18) или в матричном виде (19). Требуется решить ее с заданной точностьюПредполагается, что
aii 0, i 1, n.
1. Более быструю скорость сходимости метода простых итераций можно обеспечить следующим
образом.
x1 k 1 xi k 1
xi k 1
xi k1 xn k
2. Итерационный процесс:
x1 k 1 1 12 x2 k 13 x3 k ... 1n xn k ,
k 1
k 1
k
k
x2 2 21x1 23 x3 ... 2 n xn ,
22
.............................................................
x k 1 x k 1 x k 1 ... x k 1 .
n
n1 1
n2 2
nn 1 n
n
3. Выбор начального приближения:
x 0 .
4. Условия окончания итерационного процесса (22):
x k 1 x k .
.
44. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие системы называются линейными?2. Какие точные методы СЛАУ Вы знаете?
3. В чем состоит преимущество численных методов перед точными?
4. Сформулируйте постановку задачи для приближенного решения СЛАУ?
5. Приведите процесс приведения СЛАУ к виду, допускающему сходящиеся итерации.
6. Сформулируйте теорему о достаточных условиях сходимости итерационного процесса по
методу простых итераций.
7. Сформулируйте теорему о необходимых и достаточных условиях сходимости
итерационного процесса по методу простых итераций.
8. Каким образом выбирается начальное приближение?
9. В чем состоит идея метода релаксации?
10. Запишите условия окончания итерационных процессов по методам простых итераций,
Зейделя и релаксации.
45. ЛЕКЦИЯ 7
МЕТОДЫ ПРИБЛИЖЕНИЯ ФУНКЦИЙ(первая интерполяционная формула
Ньютона)
46. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Задача интерполяции функций возникает в тех случаях, когда:1) функция задана в виде таблицы узловых точек (Табл.1) и необходимо знать значения
функции для аргументов, расположенных в таблице между узлами
xi , i 0, n,
а также для аргументов,
не принадлежащих таблице;
Табл.1
xi
yi
x0
y0
x1 xn
y1 yn
2) функция задана в виде таблицы и необходимо определить ее аналитическое выражение;
3) известно аналитическое выражение функции, но вследствие его сложного вида, возникает
необходимость представления этой функции в более простом виде (задачи численного
дифференцирования и численного интегрирования).
Построив интерполяционный полином любого порядка можно уплотнить таблицу, вычисляя
значения полинома для аргументов, расположенных в таблице между узловыми точками. Также
можно расширить таблицу как вправо, так и влево, вычисляя значения полинома в точках, не
принадлежащих таблице (задача экстраполяции).
47. ПОСТАНОВКА ЗАДАЧИ ИНТЕРПОЛЯЦИИ И АППРОКСИМАЦИИ ФУНКЦИЙ
Классический подход к численному решению подобных задач заключается в том, чтобы, опираясь на информацию о функции f xпо некоторому алгоритму подобрать аппроксимирующую
функцию F x в определенном смысле «близкую» к f x
связана с критерием согласия:
. Часто процедура аппроксимации
f x , F x min f xi F xi
n
2
i 0
Применяемый на его основе способ аппроксимации называется методом наименьших квадратов.
Для функций, заданных таблично, достаточно распространенным критерием согласия является
критерий Чебышева, который определяет расстояние
между аппроксимируемой и
аппроксимирующей функциями как максимум величины отклонения между ними в узлах сетки:
f x , F x max f xi F xi
Если f x , F x 0
т.е.
f xi F xi yi
а процедуру вычисления значений
сетки, - интерполированием.
f x
0 i n
, то способ аппроксимации называется интерполяцией,
с помощью F x
в точках, не являющихся узлами
48. ПОСТАНОВКА ЗАДАЧИ ИНТЕРПОЛЯЦИИ И АППРОКСИМАЦИИ ФУНКЦИЙ
На отрезке a, b заданыn 1 точки x0 , x1,..., xn
и значения некоторой функции f x
, которые называются узлами интерполяции,
в этих точках:
f x0 y0 , f x1 y1,..., f xn yn
Необходимо построить интерполирующую функцию F x
(25)
, принадлежащую некоторому классу
и принимающую в узлах интерполяции заданные значения (25), т.е.
F xi yi , i 0, n
(26)
Геометрически это означает, что нужно найти кривую y F x определенного типа, проходящую
через заданные точки M i xi , yi . Данная задача является однозначной, если вместо произвольной функции F x
искать полином Pn x степени не менее n
удовлетворяющий условиям (26):
Pn x0 y0 , Pn x1 y1,..., Pn xn yn
Полученную интерполяционную функцию y F x
значений данной функции f x
используют для приближенного вычисления
в точках, отличных от узлов интерполяции. Такая операция
называется интерполированием функции.
49. КОНЕЧНЫЕ РАЗНОСТИ. ОБОБЩЕННАЯ СТЕПЕНЬ.
Пусть задана функция y f x . Обозначим через x hфиксированную величину
приращения аргумента (шаг). Тогда выражение y f x f x x f x
конечной разностью функции y f x
называется первой
. Аналогично определяются конечные разности высших
порядков, которые обозначаются n y n 1 y , n 2,3,...
Символ
оператор ставящий в соответствие функции
y f x
функцию y f x x f x
Основные свойства оператора :
1) U V U V
2) cU c U , c const
3) m n y n m y
Получим:
где m, n Z
(целые неотрицательные числа), причем
f x n x 1 f x
n
0 y y
50. КОНЕЧНЫЕ РАЗНОСТИ. ОБОБЩЕННАЯ СТЕПЕНЬ.
Определение. Обобщенной n-й степенью числа x называется произведение n
сомножителей, первый из которых равен x
, а каждый следующий на h
меньше предыдущего:
n
x x x h x 2h ... x n 1 h
где h const .
Полагают, что x 0 1
. При h 0
обобщенная степень совпадает с обычной:
n
x x n
Вычислим конечные разности для обобщенной степени, полагая
x h
Первая конечная разность: x n h n x n 1
Вторая конечная разность:
2 x h 2n n 1 x
n
n 2
Окончательно получим:
k x hnn n 1 ... n k 1 x
n
n
k x 0 если
k n
n k
, k 1, n
51. ПЕРВАЯ ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА.
Пусть для функции y f xзаданы значения yi f xi
значений независимой переменной
подобрать полином Pn x
xi x0 ih, i 0, n
степени, не выше n
где h
для равноотстоящих значений
- шаг интерполяции. Требуется
, принимающей в точках
xi
значения
Pn xi yi , i 0, n
Будем искать полином в виде
Pn x a0 a1 x x0 a2 x x0 x x1 ...
an x x0 x x1 ... x xn 1
(28)
Используя понятие обобщенной степени, запишем выражение (28) в виде:
1
2
n
(29)
Pn x a0 a1 x x0 a2 x x0 ... an x x0
Определим коэффициенты ai , i 0, n
. Полагая x x0
в выражении (29) получим
Pn x0 y0 a0
Чтобы найти коэффициент a1
, составим первую конечную разность:
1
n 1
Pn x a1h 2a2h x x0 ... nhan x x0
52. ПЕРВАЯ ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА.
Полагаяx x0
Полагая
x x0
Следовательно:
получим Pn x0 y0 a1h
получим
. Следовательно
Pn x0 y0 2!h a2
2
2
k y0
ak
, k 0, n
k !h k
2
, причем:
a1
y0
h
. Следовательно
2 y0
a2
2!h 2
0! 1, 0 y y
Интерполяционный полином Ньютона:
2
y0
n y0
1 y0
2
Pn x y0
x x0 2 x x0 ... n x x0 n
1!h
2!h
n!h
Для практического использования формулы Ньютона введем новую переменную:
Первый интерполяционный полином Ньютона:
q q 1 2
q q 1 ... q n 1 n
Pn x y0 q y0
y0 ...
y0
2!
n!
При
q
x x0
h
(40)
n 1 получим формулу линейного интерполирования:
Pn x y0 q y0
При n 2
получим формулу квадратичного интерполирования:
q q 1 2
Pn x y0 q y0
y0
2!
Первая интерполяционная формула Ньютона предназначена для интерполирования функции
в окрестности начальной точки.
53. КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Что называется конечной разностью?2. Запишите свойства оператора
.
3. Что называется обобщенной степенью числа?
4. Запишите формулу, по которой вычисляется первая конечная разность
n
-й обобщенной
степени.
5. Запишите формулы, по которым вычисляются k
степени, при k n и
k n
-е конечные разности для обобщенной
.
6. В чем суть задачи интерполирования?
7. Что называется интерполированием и экстраполированием функции?
8. Какие интерполяционные формулы используются для равноотстоящих узлов?
9. Запишите первую интерполяционную формулу Ньютона.
10. Для интерполирования в окрестности какой точки используется первая интерполяционная
формула Ньютона?
11. Чему равна погрешность первой интерполяционной формулы Ньютона?
54. ЛЕКЦИЯ 8
МЕТОДЫ ПРИБЛИЖЕНИЯ ФУНКЦИЙ(вторая интерполяционная формула Ньютона,
интерполяционная формула Лагранжа, задача
аппроксимации)
55. ВТОРАЯ ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА
Вторая интерполяционная формула Ньютона применяется для интерполирования вокрестности конечного значения xn .
Пусть для функции y f x заданы значения yi f xi для равноотстоящих
значений независимой переменной
xi x0 ih, i 0, n
Построим полином следующего вида:
Pn x a0 a1 x xn a2 x xn x xn 1 ...
an x xn x xn 1 ... x x1 .
Используя обобщенную степень, получим:
1
2
n
Pn x a0 a1 x xn a2 x xn 1 ... an x x1
Найдем коэффициенты ai из условий:
Pn xi yi , i 0, n
При
x xn
Тогда:
: Pn xn yn a0
i Pn xn i i yn i , i 0, n
k yn k
ak
, k 0, n
k !h k
Вторая интерполяционная формула Ньютона:
yn 1
2 yn 2
Pn x yn
x xn
x xn x xn 1 ...
1!h
2!h 2
n y0
x xn ... x x1 .
n!h n
56. ВТОРАЯ ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА
ОбозначимВТОРАЯ ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА
НЬЮТОНА
x xn
t
, тогда
h
x xn k x xn kh
t k , k 0, n 1.
h
h
Вторая интерполяционная формула Ньютона:
t t 1 2
t t 1 t 2 3
Pn x yn t yn 1
yn 2
yn 3 ...
2!
t t 1 ... t n 1 n
y0 .
n!
3!
Пусть на отрезке a, b задана произвольная система точек xi , i 0, n , в которых
известны значения функции yi f xi , i 0, n т.е. задана следующая таблица:
Табл.2
xi
yi
Построим многочлен
Pn x
x0
y0
x1 xn
y1 yn
таким образом, чтобы
Pn xi yi , i 0, n
57. ВТОРАЯ ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА
ВТОРАЯ ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛАНЬЮТОНАn в виде:
Лагранж предложил строить многочлен степени
Pn x a0 x x1 x xn a1 x x0 x x2 x xn an x x0 x xn 1
Найдем коэффициенты Лагранжа
При
x x0
ai , i 0, n
из условия (32).
: Pn x0 y0 .
Pn x0 a0 x0 x1 x0 x2
Коэффициент
a0
x0 xn y0
вычисляется по следующей формуле:
a0
y0
x0 x1 x0 x2 ... x0 xn
Интерполяционный полином Лагранжа:
Pn x y0
x x1 x xn y x x0 x x2 x xn y x x0 x xn 1
n
x0 x1 x0 xn 1 x1 x0 x1 x2 x0 xn
xn x0 xn xn 1
58. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА
Пример. По заданной системе точекТабл.3
xi
yi
0.524
6
0.5
0.785
4
0.707
1.571
2
1.0
построить интерполяционный полином Лагранжа второго порядка вида:
P2 x a0 x x1 x x2 a1 x x0 x x2 a2 x x0 x x1
Коэффициенты
Лагранжа:
y0
y1
y2
a0
1.824
a1
3.439
a2
1.216
x0 x1 x0 x2
x1 x0 x1 x2
x2 x0 x2 x1
Полином
порядка:
Лагранжа
второго
P2 x 1.824 x x1 x x2 3.439 x x0 x x2
1.216 x x0 x x1 0.4 x 2 1.32 x 0.08.
59. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА
Если таблица 2, для которой построена формула Лагранжа, задана дляравноотстоящих узловых точек xi 1 xi h, i 0, n 1 , то данная формула
x x0
h
1 q 1
упрощается. Обозначим через
x x1 x x0 h x x0
h
h
h
q
. Тогда
Формула Лагранжа запишется так:
Pn q y 0
x xi
q i, i 0, n
h
q 1 q n y
q q 2 q n
q q n 1
yn
1
q0 q1 q0 qn
q1 q0 q1 q2 q1 qn
qn q0 qn qn 1
При n 1 получим формулу линейной интерполяции:
P1 x y0 q y0
Здесь yi yi yi 1, i 1,2,... табличные разности первого порядка.
При n 2 получим формулу квадратичной интерполяции: P2 x y0 q y0 q q 1 2 y0
2
Здесь 2 yi yi 1 yi , i 1,2,... табличные разности второго порядка.
Первая интерполяционная формула Ньютона:
q q 1 q n 1 n
q q 1 2
Pn q y0 q y0
y0
y0
x x
Если t h n
, то
2!
x xn i
t i, i 0, n
h
n!
Вторая интерполяционная формула Ньютона:
Pn t yn t yn 1
t t 1 2
t t 1 ... t n 1 n
yn 2 ...
y0
2!
n!
60. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ (ЗАДАЧА АППРОКСИМАЦИИ)
По данным эксперимента (таблица 4) необходимо построить приближеннофункцию, отображающую зависимость ее от x, в виде многочлена с тем
расчетом, чтобы сумма квадратов отклонений построенной функции от
экспериментальной в узловых точках была бы минимальной. Будем строить
искомую функцию в виде многочлена
f x an xn an 1xn 1 a1x a0
Формула Лагранжа запишется так:
Табл.4
xi
yi
x0
y0
x1 xm
y1 ym
Определим коэффициенты ai , i 0, n . Введем функцию
m
min S min i2
i 0
Здесь
узловых точках
i f xi yi
xi , i 0, m
m
S i2
i 0
и определим
отклонение функции от экспериментальной в
. СЛАУ
m
m
m
m
2
n
m
1
a
x
a
x
a
x
a
0 i1 i 2
i n yi ;
i 0
i 0
i 0
i 0
m
m
m
m
2
n 1
xi a0 xi a1 xi an xi yi ;
i 0
i 0
i 0
i 0
...
m
m
m
m n
n 1
2n
n
x
a
x
a
x
a
i 1
i n xi yi .
i 0
i
0
i 0
i 0
i 0
61. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ (ЗАДАЧА АППРОКСИМАЦИИ)
Пример. По заданной системе точек (таблица 3) из примера 7 построитьаппроксимационные многочлены первого P1 x a1x a0 и второго порядка
P2 x a2 x2 a1x a0 методом наименьших квадратов.
Построение многочлена первого порядка.
1.
2.
3.
2
xi 2.88;
i 0
2
xi 3.358;
2
i 0
2
yi 2.207;
i 0
2
xi yi 2.388
i 0
3a0 2.88a1 2.207;
2.88a0 3.358a1 2.388.
a0 0.03; a1 0.454.
4. Искомый многочлен первого порядка: P x 0.03x 0.454
1
Построение многочлена второго порядка.
2
2
2
1. xi3 4.504; xi4 6.544; xi2 yi 3.041
i 0
i 0
i 0
3a0 2.88a1 3.358a2 2.207;
2. 2.88a0 3.358a1 4.504a2 2.388;
3.358a 4.504a 6.544a 3.041.
0
1
2
3. a0 0.004; a1 1.146; a2 0.323
4. Искомый многочлен второго порядка:
P2 x 0.323x2 1.146 x 0.004
62. КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Для каких узлов используется вторая интерполяционная формула Ньютона?2. Для интерполирования в окрестности какой точки используется вторая
интерполяционная формула Ньютона?
3. Запишите вид полинома, используемого для получения второй интерполяционной
формулы Ньютона?
4. Чему равны коэффициенты второй интерполяционной формулы Ньютона?
5. Запишите вторую интерполяционную формулу Ньютона.
6. Чему равна погрешность второй интерполяционной формулы Ньютона?
7. Для каких узлов используется интерполяционная формула Лагранжа?
8. Запишите интерполяционную формулу Лагранжа.
9. Чему равна погрешность интерполяционной формулы Лагранжа?
10. В каких случаях возникает задача аппроксимации?
11. В чем суть метода наименьших квадратов?
12. В каких случаях возникает задача аппроксимации экспоненциальными функциями?
63. ЛЕКЦИЯ 9
ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ(формулы численного дифференцирования,
основанные на первой интерполяционной формуле
Ньютона и на интерполяционной формуле
Лагранжа)
64. ПОСТАНОВКА ЗАДАЧИ
При решении практических задач часто требуется найти производныеразличных порядков от функций, заданных таблицей, или функций, имеющих
сложный аналитический вид. В этих случаях прибегают к приближенному
дифференцированию.
Для этого на отрезке a, b функцию y f x
F x
заменяют интерполирующей функцией
(чаще всего интерполирующим полиномом Pn x ), затем полагают
f x F x
Y F x
при a x b
. Близость друг к другу ординат двух кривых y f x и
на отрезке a, b еще не гарантирует близости на этом отрезке их
производных
f x
и
F x
, т.е. малого расхождения угловых коэффициентов
касательных к рассматриваемым кривым при одинаковых значениях аргумента.
65. ФОРМУЛЫ ПРИБЛИЖЕННОГО ДИФФЕРЕНЦИРОВАНИЯ, ОСНОВАННЫЕ НА ПЕРВОЙ ИНТЕРПОЛЯЦИОННОЙ ФОРМУЛЕ НЬЮТОНА
Пусть на отрезке a, b заданы равноотстоящие точкиxi x0 ih, i 0, n
где h
b a
n
,и
известны значения функции в этих точках yi f xi , i 0, n . Требуется найти
производные f x , f x ,... на отрезке a, b .
Если воспользоваться первой интерполяционной формулой Ньютона, то получим:
q q 1 2
q q 1 q 2 3
y x Pn x y0 q y0
y0
y0
2!
где q
x x0
h
q q 1 q 2 q 3 4
y0
4!
q q 1
3!
q n 1
n!
n y0 ,
.
Аналогично:
1 2
6q 2 18q 11 4
3
y x 2 y0 q 1 y0
y0
12
h
Если подсчитать производные в узлах интерполяции при
1
1
1
1
y x y0 2 y0 3 y0 4 y0
h
2
3
4
x x0 , q 0
, получим:
66. ФОРМУЛЫ ЧИСЛЕННОГО ДИФФЕРЕНЦИРОВАНИЯ ДЛЯ РАВНООТСТОЯЩИХ ТОЧЕК, ОСНОВАННЫЕ НА ИНТЕРПОЛЯЦИОННОЙ ФОРМУЛЕ ЛАГРАНЖА
Пусть даны равноотстоящие точкиxi , i 0, n
такие, что xi x0 ih , и известны
значения функции в этих точках: yi f xi , i 0, n . Для данной системы узлов
yi f xi
построим интерполяционный полином Лагранжа:
x x0 ... x xi 1 x xi 1 ... x xn
xi x0 ... xi xi 1 xi xi 1 ... xi xn
i 0
n
n 1 x yi
,
x
x
x
i 0
i
n 1 i
n
Ln x yi
где n 1 x x x0 ... x xi ... x xn
Для Ln x справедливо соотношение:
Ln xi yi
67. ФОРМУЛЫ ЧИСЛЕННОГО ДИФФЕРЕНЦИРОВАНИЯ ДЛЯ РАВНООТСТОЯЩИХ ТОЧЕК, ОСНОВАННЫЕ НА ИНТЕРПОЛЯЦИОННОЙ ФОРМУЛЕ ЛАГРАНЖА
Введем новую переменную:q
x x0
h
, тогда:
n 1 x h n 1 q q 1 ... q n h n 1q n 1
n 1 xi xi x0 ... xi xi 1 xi xi 1 ... xi xn
hn i i 1 ...1 1 ... n i 1
Получим:
n i
h n i ! n i !
n i
1 yi q n 1
Ln x
q i
i 0 i ! n i !
n
Заменив функцию y x интерполяционным полиномом Лагранжа Ln x и,
учитывая, что dLn x dLn x dq 1 dLn x из соотношения (35) получим:
dx
dq
dx
h
dq
n i
n 1
1 n 1 yi d q
y x Ln x
h i 0 i ! n i ! dq q i
Аналогично можно найти
y x
и т.д.
68. КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Когда применяется численное дифференцирование?2. Какая задача является менее точной: задача интерполирования или задача численного
дифференцирования?
3. Какие формулы используются для получения формул численного дифференцирования?
4. Как определяется погрешность производной функций?
5. Запишите формулу численного нахождения первой производной, основанную на
первой интерполяционной формуле Ньютона.
6. Какую погрешность имеет формула численного дифференцирования, полученная из
первой интерполяционной формулы Ньютона?
7. Запишите формулу численного нахождения второй производной, основанную на
первой интерполяционной формуле Ньютона.
8. Для каких узлов применяются формулы численного дифференцирования, основанные
на интерполяционной формуле Лагранжа?
9.
Запишите
формулу
численного
дифференцирования,
основанную
на
интерполяционной формуле Лагранжа.
10. Чему равна погрешность формулы численного дифференцирования, основанной на
интерполяционной формуле Лагранжа?
69. ЛЕКЦИЯ 10
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ(квадратурная формула Ньютона-Котеса,
частные случаи формулы Ньютона-Котеса
(формула трапеций, формула Симпсона))
70. КВАДРАТУРНАЯ ФОРМУЛА НЬЮТОНА-КОТЕСА
Формула Ньютона-Лейбница:b
f x dx F b F a
a
Однако, во многих случаях первообразная F x не может быть найдена с
помощью элементарных средств или являться слишком сложной; вследствие этого
вычисление определенного интеграла по формуле (36) может быть затруднено
или быть практически не выполнимым. Поэтому важное значение приобретают
численные методы вычисления определенных интегралов, использующих ряд
значений подынтегральной функции в точках
xi a, b , i 0, n
Определение. Численное вычисление однократного интеграла называется
механической квадратурой, двойного интеграла – механической кубатурой.
Соответствующие формулы называются квадратурными и кубатурными
формулами.
71. КВАДРАТУРНАЯ ФОРМУЛА НЬЮТОНА-КОТЕСА
Рассмотрим один из способов вычисления однократных интегралов.Приближенная квадратурная формула:
b
b
b
xn n
n
a
a
a
x0 i 0
i 0
f x dx ydx Ln x dx ai x yi dx Ai yi
Выведем явные выражения для коэффициентов
Введем обозначения:
q
x x0
h
Ai
, q n 1 q q 1 q n . Тогда
1 n i q n 1 y dx n A y
ii
i
i
!
n
i
!
q
i
i
0
i 0
x0
xn n
n i
n 1
1
q
dx
, где Ai
i
!
n
i
!
q
i
x0
xn
Коэффициенты Котеса:
n i n n 1
1 1
q
Hi
dq, i 0, n
n i ! n i ! 0 q i
Квадратурная формула Ньютона-Котеса:
b
n
a
i 0
ydx b a H i yi
72. ЧАСТНЫЕ СЛУЧАИ КВАДРАТУРНОЙ ФОРМУЛЫ НЬЮТОНА-КОТЕСА
ФОРМУЛА ТРАПЕЦИЙПри n 1 :
1
1
H 0 q 1 dq
2
0
;
1
1
H1 qdq
2
0
x1
h
; ydx 2 y0 y1 - формула трапеций.
x0
Рассмотрим общий случай, когда отрезок a, b произвольной длины.
xn 1, xn
Разделим отрезок на n равных частей: x0 , x1 , x1, x2 , …
и к каждому из них применим формулу трапеций:
b
x1
x2
xn
a
x0
x1
xn 1
ydx ydx ydx ... ydx
h
h
h
y0 y1 y1 y2 ... yn 1 yn
2
2
2
y
y
h 0 y1 y2 ... yn 1 n ,
2
2
где h
При
b a
n
n 2
. Формула (40) называется общей формулой трапеций.
: H 16 ; H 32 ; H 16
0
1
2
f x dx
b
a
h
y0 4 y1 y2
3
- формула Симпсона (формула парабол).
73. КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Что называется механической квадратурой?2. Что называется механической кубатурой?
3. Как называются формулы для приближенного вычисления однократных интегралов?
4. Запишите коэффициенты Котеса.
5. Запишите квадратурную формулу Ньютона-Котеса.
6. Сформулируйте свойства коэффициентов Котеса.
7. Назовите основные частные случаи формулы Ньютона-Котеса.
8. Запишите формулу трапеций.
9. Запишите квадратурную формулу Симпсона.
10. Запишите общую формулу трапеций.
11. Чему равна погрешность формулы трапеций?
12. Чему равна погрешность квадратурной формулы Симпсона?
74. ЛЕКЦИЯ 11
ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕФУНКЦИЙ
(квадратурная формула Гаусса)
75.
КВАДРАТУРНАЯ ФОРМУЛА ГАУССАОпределение. Полиномы вида
n
1 dn 2
x
1
2,...
, n 0,1,
2n n! dx n
Pn x
называются полиномами Лежандра.
Полиномы Лежандра обладают следующими свойствами:
1) Pn 1 1, Pn 1 1 n , n 0,1,
2,...
1
;
2) Pn x Qk x dx 0 , где
Qk x
- любой полином степени
3) полином Лежандра
Pn x
имеет
k
, меньшей
1
n
различных и действительных
корней, которые расположены на интервале
1,1 .
Свойство 2 называется свойством ортогональности полиномов Лежандра.
n
;
76.
КВАДРАТУРНАЯ ФОРМУЛА ГАУССАРассмотрим функцию
, заданную на отрезке 1,1 . Поставим задачу:
y f x
как нужно подобрать точки t1, t2 ,..., tn и коэффициенты
квадратурная формула
1
n
1
i 1
A1, A2 ,..., An
, чтобы
f t dt Ai f ti
была точной для всех полиномов
f t
наивысшей возможной степени
Так как в распоряжении имеется 2n постоянных ti
степени 2n 1 определяется
2n
и
Ai , i 1, n
, а полином
коэффициентами. Полагая, что
1
n
1
i 1
k
k
t dt Aiti , k 0,2n 1
и
2 n 1
f t Ck t
k 0
(41)
k
,
будем иметь:
1
1 2 n 1
2 n 1
1
2 n 1
n
n
2 n 1
1
1 k 0
k 0
1
k 0
i 1
i 1
k 0
k
k
k
k
f t dt Ck t dt Ck t dt Ck Aiti Ai Ck ti
n
Ai f ti .
i 1
N
.
77.
КВАДРАТУРНАЯ ФОРМУЛА ГАУССАУчитывая соотношения:
1 1 k 1
k 1 1
2
t
k
, если k четное;
t
dt
k 1
k 1
k
1
1
0, если k нечетное,
1
1
заключаем, что для решения задачи достаточно определить
системы
2n
уравнений:
n
Ai 2;
i 1
n
Aiti 0;
i
1
...
n
2
Aiti2 n 2
;
2n 1
i 1
n
Aiti2 n 1 0.
i 1
Система (42) – нелинейная, состоящая из
ti
и
Ai
из
(42)
2n
уравнений с 2n неизвестными ti
и Ai , i 1, n . Определитель этой системы является определителем Вандермонда:
ti t j 0
i j
Формула (41), где ti - нули полиномов Лежандра
Pn t
и Ai , i 1, n определяются
из системы (42), называется квадратурной формулой Гаусса.
78.
КВАДРАТУРНАЯ ФОРМУЛА ГАУССАНеудобство применения квадратурной формулы Гаусса состоит в том, что
абсциссы точек ti и коэффициенты
Ai
- в общем случае иррациональные
числа. Этот недостаток отчасти искупается ее высокой точностью при
сравнительно малом числе ординат.
b
Для вычисления однократного интеграла f x dx по квадратурной формуле
a
Гаусса делают замену:
x
Тогда:
где
ti
b
b a b a
t
2
2
1
b a
b a n
b a b a
b a b a
Ai f
ti
f x dx 2 f 2 2 t dt 2
2
2
i 1
a
1
нули полинома Лежандра, i 1, n .
Соотношение (43) – квадратурная формула Гаусса для вычисления
однократного интеграла.
(43)
79. КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Дайте определение полинома Лежандра.2. Запишите свойства полинома Лежандра.
3. Какое свойство называется свойством ортогональности полинома Лежандра?
4. Запишите квадратурную формулу Гаусса.
5. Для какого отрезка интегрирования применяется квадратурная формула Гаусса?
6. Из какой системы определяются коэффициенты Ai , t i ?
7. В чем состоит неудобство применения квадратурной формулы Гаусса?
8. Какая замена делается для вычисления двойного интеграла по квадратурной формуле
Гаусса на произвольном отрезке?
9. Запишите квадратурную формулу Гаусса для произвольного интеграла.
10. Чем являются коэффициенты
ti
в квадратурной формуле Гаусса?
80. ЛЕКЦИЯ 12
ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕФУНКЦИЙ
(приближенное вычисление несобственных
интегралов)
81.
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ НЕСОБСТВЕННЫХИНТЕГРАЛОВ
b
Определение. Интеграл f x dx называется собственным, если:
a
1) Промежуток интегрирования a, b конечен;
2) Подынтегральная функция f x непрерывна на a, b .
В противном случае, интеграл называется несобственным.
I. Несобственный интеграл
f x dx
(44)
a
Определение. Интеграл (44) называется сходящимся, если существует
конечный предел
b
lim f ( x)dx
b a
. Если предел
интеграл (44) называется расходящимся.
b
lim f ( x)dx
b a
, не существует, то
82.
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ НЕСОБСТВЕННЫХИНТЕГРАЛОВ
Вычисление сходящегося несобственного интеграла с заданной точностью
b
a
a
b
f x dx f x dx f x dx
Тогда:
(46)
f x dx S
a
II. Допустим, что отрезок a, b конечен, а функция f ( x) имеет конечное число
точек разрыва на отрезке. Если
c
внутренняя точка отрезка, то полагают:
b
c 1
f
x
dx
lim
f
x
dx
f
x
dx
0
1
a
c 2
a
0
b
(49)
2
и в случае существования этого предела интеграл называют сходящимся, в
противном случае – расходящимся.
:
83. КУБАТУРНЫЕ ФОРМУЛЫ ТИПА СИМПСОНА
zz f x, y
0
a
x
b
B
y
A
D
84.
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ДВОЙНЫХИНТЕГРАЛОВ
Так как двойной интеграл вычисляется через повторный, то при приближенном
вычислении
двойного
интеграла
можно
использовать,
например,
квадратурную формулу Симпсона.
1) Вычислим f x, y dxdy , где область D - это прямоугольник вида:
D
D a x A, b y B
Каждый отрезок a, A , b, B
разобьем пополам точками
x0 a, x1 a h, x2 a 2h A;
где
А а
h
2
B b
, k
2
.
y0 b, y1 b k , y2 b 2k B,
Расписав двойной интеграл через повторный, и применив два раза квадратурную
формулу Симпсона, получим кубатурную формулу Симпсона:
f x, y dxdy dx f x, y dy
D
A
B
a
b
A
A
k A A
f x, y0 dx 4 f x, y1 dx f x, y 2 dx dx
3 a a
a
a
hk
f x0 , y0 4 f x1 , y0 f x2 , y0 4 f x0 , y1 4 f x1 , y1 f x2 , y1 f x0 , y 2 4 f x1 , y 2 f x2 , y 2 .
9
(50)
85.
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ДВОЙНЫХИНТЕГРАЛОВ
2) Отрезок a, A разобьем на
2n
равных частей. Выбирая шаги
h
четное число прямоугольников.
равных частей, отрезок b, B - на
A a
2n
и
k
B b
2m
2m
делим прямоугольник на
Обобщенная кубатурная формула Симпсона:
f x, y dxdy
D
hk 2n 2m
ji fij
9 i 0 j 0
3) Если D является произвольной криволинейной областью, то строится
прямоугольник D содержащий область D
, причем стороны прямоугольника
D
параллельны осям координат.
Рассматривается вспомогательная функция
f x, y , если x, y D;
f * x, y
0, если x, y D / D.
*
Тогда f x, y dxdy f x, y dxdy
D
D
и, применяя к последнему интегралу обобщенную кубатурную формулу Симпсона,
получим приближенное значение двойного интеграла по произвольной
криволинейной области.
86. КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Какой интеграл называется сходящимся?2. Дайте определение сходящегося несобственного интеграла с бесконечным интервалом
интегрирования.
3. Как вычисляется несобственный интеграл с бесконечным интервалом интегрирования?
4. Дайте определение сходящегося несобственного интеграла, если подынтегральная
функция имеет разрыв на конечном отрезке интегрирования.
5. Как вычисляется несобственный интеграл, если подынтегральная функция имеет
разрыв на конечном отрезке интегрирования?
6. Как называется формула, применяемая для приближенного вычисления двойного
интеграла?
7. Как выбирается шаг для приближенного вычисления двойного интеграла?
8. Запишите кубатурную формулу Симпсона.
9. Запишите обобщенную кубатурную формулу Симпсона.
10. Запишите кубатурную формулу Симпсона для произвольной криволинейной области.
87. ЛЕКЦИЯ 13
ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ И СИСТЕМ
(методы Эйлера, Рунге-Кутта и Адамса)
88.
ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ОБЫКНОВЕННЫХДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ И СИСТЕМ
Методы решения обыкновенных дифференциальных уравнений:
1) аналитические методы;
2) приближенные методы.
Решить дифференциальное уравнение
y f x, y
(50)
численным методом означает, что для заданной последовательности аргументов
x0 , x1, x2 , . . ., xn
y F x
и числа y0 y x0 , не определяя аналитического вида функции
, нужно найти значения y1, y2 , . . . , yn
, удовлетворяющие условиям:
F x0 y0 , yk F xk , k 1, n
89.
МЕТОД ЭЙЛЕРАПусть дано дифференциальное уравнение (50) с начальным условием (задача
Коши) y0 y x0 и выполняются условия существования и единственности
решения.
Теорема Пиккара. Если в уравнении (50) f x, y непрерывна в
функция
D x0 a x x0 a; y0 b y y0 b и удовлетворяет в D
прямоугольнике
условию Липшица:
f x, y1 f x, y2 N y1 y2
- константа Липшица, то существует единственное решение y y x ,
y x0 y0 где
x0 H x x0 H уравнения (50), удовлетворяющее условию
где N
b 1
H min a, ,
M N
, M max f x, y .
D
Рабочая формула метода Эйлера:
yi 1 yi h f xi , yi , i = 0, n
(52)
Метод Эйлера может быть применен к решению систем обыкновенных
дифференциальных уравнений.
Достоинством метода Эйлера является его простота и высокая скорость поиска
решения (одношаговый метод). Недостатками метода Эйлера является малая
точность и систематическое накопление ошибок.
90.
МЕТОД РУНГЕ-КУТТА ЧЕТВЕРТОГО ПОРЯДКАМетод Рунге-Кутта имеет высокую точность, но не высокую скорость поиска
решения (многошаговый метод).
Рассмотрим числа:
k1i hf xi , yi ;
k
h
k2i hf xi , yi 1i ;
2
2
k
h
k3i hf xi , yi 2i ;
2
2
k4i hf xi h, yi k3i .
Рабочая формула метода Рунге-Кутта четвертого порядка имеет вид:
yi 1 yi
1
k1i 2k2i 2k3i k4i
6
Метод Рунге-Кутта обладает значительной точностью, и, несмотря на свою
трудоемкость,
широко
используется
при
численном
решении
дифференциальный уравнений и систем.
91.
МЕТОД АДАМСАЭкстраполяционная формула Адамса:
1
5
3
yi 1 yi hyi hyi 1 2 hyi 2 3 hyi 3
2
12
8
Для начала итерационного процесса нужно знать начальные значения
зная которые находят
y0 , y1 , y2 , y3
y0 , y1, y2 , y3
,
и составляют таблицу конечных разностей:
hy0 , hy1 , hy2 , 2 hy0 , 2 hy1 , 3 hy0
Для работы на ЭВМ формулу Адамса применяют в раскрытом виде. Так как
yi 1 yi yi 1;
2 yi 2 yi 2 yi 1 yi 2 ;
3 yi 3 yi 3 yi 1 3 yi 2 yi 3 ,
то:
h
55 yi 59 yi 1 37 yi 2 9 yi 3 ;
24
xi 1 xi h.
yi 1 yi
Метод Адамса легко распространяется на системы дифференциальных уравнений.
Погрешность метода Адамса имеет тот же порядок, что и метод Рунге-Кутта.
92. КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Какие уравнения называются обыкновенными дифференциальными уравнениями?2. Когда возникает задача приближенного решения обыкновенных дифференциальных
уравнений и систем?
3. Какие методы приближенного решения обыкновенных дифференциальных уравнений Вы
знаете?
4. Сформулируйте постановку задачи для метода Эйлера.
5. Как выбирается шаг в методе Эйлера?
6. Запишите формулу Эйлера.
7. Какую погрешность имеет метод Эйлера?
8. Назовите достоинства и недостатки метода Эйлера.
9. Сформулируйте постановку задачи для метода Рунге-Кутта четвертого порядка точности.
10. Запишите итерационную формулу метода Рунге-Кутта четвертого порядка точности.
11. Какую погрешность имеет формула Рунге-Кутта четвертого порядка точности?
12. Запишите итерационную формулу метода Рунге-Кутта второго порядка точности. Какова ее
погрешность?
13. Как определяется правильность выбора шага в методе Рунге-Кутта?
14. Назовите достоинства и недостатки метода Рунге-Кутта.
15. Запишите экстраполляционную формулу Адамса.
16. Как выбирается шаг в методе Адамса?
17. Какую погрешность имеет метод Адамса?
93. ЛЕКЦИЯ 14
КРАЕВЫЕ ЗАДАЧИ ДЛЯДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ВТОРОГО
ПОРЯДКА
(метод прогонки)
94.
ПОСТАНОВКА ЗАДАЧИРассмотрим простейшую двухточечную краевую задачу.
Пример. Найти функцию y y x удовлетворяющую дифференциальному
уравнению второго порядка вида:
y f x, y, y
и принимающую при
x a и x b a b
Пример. Найти такое решение
(57)
заданные значения
y a A; y b B
y y x
.
дифференциального уравнения (57)
чтобы производные имели заданное значение y a A1; y b B1 .
Пример. Найти решение дифференциального уравнения (57),
удовлетворяющего условиям:
y a A, y b B1
.
Пример. Найти решение дифференциального уравнения (57),
удовлетворяющего условиям:
y a A1, y b B .
95.
КОНЕЧНО-РАЗНОСТНАЯ СХЕМАДано дифференциальное уравнение (57) с краевыми условиями:
0 y a 1 y a A;
0 y b 1 y b B,
Линейное дифференциальное уравнение:
y p x y q x y f x
(58)
с краевыми условиями:
0 y a 1 y a A,
0 y b 1 y b B,
где
02 12 0, 02 12 0
.
(59)
96.
КОНЕЧНО-РАЗНОСТНАЯ СХЕМАУравнение (58) заменим конечно-разностными уравнениями:
yi 1 2 yi yi 1
yi 1 yi 1
p
qi yi fi
i
2h
h2
,
i 1, n 1
(60)
Конечно-разностные уравнение:
y1 y0
1 y0 A;
h
y yn 1
0 n
1 yn B.
h
0
Запишем систему (58) в канонической форме:
yi 1 2 hpi yi 2h2qi 4 yi 1 2 hpi 2h2 fi
2h2qi 4
2 hpi 2h 2 fi
yi 1 yi
yi 1
2 hpi
2 hpi 2 hpi
Введем обозначения:
Получим:
yi 1 mi yi ri yi 1 i
,
,
i 1, n 1
2h2qi 4
2 hpi
2h 2 f i
mi
, ri
, i
.
2 hpi
2 hpi
2 hpi
,
i 1, n 1
.
i 1, n 1
97.
КОНЕЧНО-РАЗНОСТНАЯ СХЕМАБудем искать
yi
в виде:
(61)
yi ci (di yi 1 )
где коэффициенты
требуется определить. Выразим
ci , di
yi 1 ci 1 di 1 yi
и подставим в исходную систему (54):
yi 1 mi yi ri ci 1 (di 1 yi ) i
Выразим из последнего соотношения
d0
Ah
0
yi
:
yi
i yi 1 ri ci 1di 1
1
i rici 1di 1 yi 1
mi ri ci 1
mi ri ci 1
Тогда
ci
Найдем
с0 , d 0
y0 c0 (d0 y1 )
1
; di i ri ci 1di 1
mi ri ci 1
,
i 1, n 1
из первого краевого условия. Выражая
, получим:
c0
0
h 1 0
,
d0
Ah
0
.
y0
Ah 0 y1
h 1 0
и сравнивая с
98.
КОНЕЧНО-РАЗНОСТНАЯ СХЕМАПрямой ход вычислений:
1. Вычисляют значения
2. Находят
.
.
с0 , d 0
3. Вычисляют
mi , ri , i , i 1, n 1
ci , d i
,
i 1, n 1
.
Обратный ход вычислений:
1. Решают систему из двух уравнений относительно
yn
и
yn 1
:
yn 1 cn 1 dn 1 yn
x0 ,..., xn
0
yn cn 1 (d n 1 yn )
1 yn B
h
Bh 0cn 1d n 1
0 1 cn 1 h 1
и получают
yn
.
2. Вычисляют
yi ci di yi 1 , i n 1,0
начиная с
3. Сравнивают полученное в п.2 со значением
Получим значения
y0 ,..., yn
yn 1
y0
и далее до
Ah 0 y1
h 1 0
y0
.
.
искомой функции в узловых точках
x0 ,..., xn
.
99. КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Сформулируйте краевую задачу для дифференциальных уравнений второго порядка.2. К решению какой системы сводится краевая задача для дифференциального уравнения
второго порядка?
3. Какие методы применяются для приближенного решения краевой задачи для
дифференциального уравнения второго порядка?
4. Запишите конечно-разностное уравнение для дифференциального уравнения второго
порядка.
5. Из скольких частей состоит метод прогонки и как они называются?
6. Для чего служит прямой ход метода прогонки?
7. Для чего служит обратный ход метода прогонки?
8. Из какого краевого условия находят коэффициенты
C0 , d0
9. Из какого краевого условия находят коэффициенты
yn
10. Запишите формулу оценки погрешности метода прогонки.
?
?
100. ЛЕКЦИЯ 15
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХЗАДАЧ ДЛЯ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
(классификация дифференциальных
уравнений с частными производными)
101.
КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ СЧАСТНЫМИ ПРОИЗВОДНЫМИ
Рассмотрим приближенные методы решения задач в общем случае для
дифференциальных уравнений в частных производных второго порядка с
двумя независимыми переменными:
F x, y, u, u x , u y , u xx , u xy , u yy 0
где
x, y
, независимые переменные;
u x , u y , u xx , u xy , u yy
u ( x, y )
(62)
- искомая функция;
- первые и вторые частные производные по аргументам
Решением уравнения (62) называется функция
u u x, y
x , y.
, обращающая это
это уравнение в тождество. График решения представляет собой поверхность в
пространстве V3
.
102.
КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ СЧАСТНЫМИ ПРОИЗВОДНЫМИ
Определение. Уравнение (62) называется вполне линейным, если оно является
уравнением первой степени относительно искомой функции и всех ее
производных и не содержит их произведений:
Au xx 2 Bu xy Cu yy Ku x Lu y Mu x, y F x, y
где коэффициенты
могут зависеть только от
A, B, C, K , L, M
Если коэффициенты
A, B, C, K , L, M
не зависят от
x, y
(63)
x, y
.
т.е. являются
постоянными, то уравнение (63) называется линейным дифференциальным
уравнением второго порядка с постоянными коэффициентами.
Пусть
дискриминант уравнения.
A B
AC B 2
B C
103.
КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ СЧАСТНЫМИ ПРОИЗВОДНЫМИ
В зависимости от знака
линейное дифференциальное уравнение (63)
относится к одному из следующих типов:
0
- эллиптический тип;
0
- параболический тип;
0
- гиперболический тип;
не сохраняет постоянного знака в данной области – смешанный тип.
Тип линейного дифференциального уравнения (63) сохраняется при любом
невырожденном преобразовании
x, y
x, y
С
линейным дифференциальным
дифференциальное уравнение
уравнением
(63)
связано
обыкновенное
A dy 2 Bdxdy C dx 0
2
2
которое называется характеристическим уравнением для дифференциального
уравнения (63).
104.
КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ СЧАСТНЫМИ ПРОИЗВОДНЫМИ
Решения характеристического уравнения (63) называются характеристиками
уравнения (63).
1. Канонический вид уравнения гиперболического типа:
u , u , u , u f ,
2. Канонический вид уравнения параболического типа:
u , u , u , u f ,
3. Канонический вид уравнения эллиптического типа:
x, y i x, y C1;
x, y i x, y C2 .
4. Канонический вид уравнения эллиптического типа:
u u , u , u , u f ,
Выражение
u u u
называется оператором Лапласа.
105. КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Какое дифференциальное уравнение с частными производными называется вполнелинейным?
2. Запишите вид вполне линейного дифференциального уравнения.
3. Как определяется тип дифференциального уравнения с частными производными?
4. Сохраняется ли тип дифференциального уравнения при любом невырожденном
преобразовании координат?
5. Запишите характеристическое уравнение для вполне линейного дифференциального
уравнения в частных производных.
6. Запишите канонический вид дифференциального уравнения гиперболического типа.
7. Запишите канонический вид дифференциального уравнения параболического типа.
8. Запишите канонический вид дифференциального уравнения эллиптического типа.
9. Запишите уравнение Лапласа и уравнение Пуассона.
10. Запишите первую основную конечно-разностную форму оператора Лапласа.
106. ЛЕКЦИЯ 16
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХЗАДАЧ ДЛЯ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
(решение задачи Дирихле методом сеток)
107.
РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ МЕТОДОМ СЕТОКИдея метода сеток (метода конечных разностей) для приближенного решения
краевых задач для двумерных дифференциальных уравнений заключается в
следующем:
1) в плоской области
D , в которой разыскивается решение, строится
сеточная область Dh , состоящая из одинаковых ячеек, и приближающая
данную область D ;
2) заданное дифференциальное уравнение заменяется в узлах построенной сетки
соответствующим конечно-разностным уравнением;
3) на основании граничных условий устанавливаются значения искомого
решения в граничных узлах области
Dh
.
108.
РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ МЕТОДОМ СЕТОКВыбор сеточной области производится в зависимости от конкретной задачи, но
во всех случаях контур h сеточной области
Dh
следует выбирать так, чтобы
он как можно лучше аппроксимировал контур заданной области D .
Рассмотрим применение метода сеток для построения решения задачи Дирихле:
2u 2u
0 x, y D
x 2 y 2
(64)
u x, y x, y
Выбрав шаг
h
, строим квадратную сетку
xi x0 ih, y j y0 jh, i, j 0, 1, 2,...
с таким расчетом, чтобы узлы
D
xi , y j сетки S h или принадлежали области
, или отстояли от ее границы на расстоянии, меньшем чем
h
.
109.
РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ МЕТОДОМ СЕТОКОпределение. Узлы сетки S h называются соседними, если они удалены друг
от друга в направлении оси OX или OY на расстоянии, равное шагу сетки h .
Ah сетки S h называется внутренним, если он принадлежит
Определение.
Узел D , а все 4 соседним с ним узла - множеству S h ; в противном случае
области
он называется граничным.
Определение. Граничный узел сетки S h называется узлом первого рода
Bh , если
он имеет соседний внутренний узел этой сетки; в противном случае граничный
узел называется узлом второго рода Ch .
Внутренние узлы Ah и граничные узлы первого рода Bh сетки S h называются
расчетными точками. Граничные узлы второго рода Ch в вычислениях не
участвуют и могут быть изъяты из сетки.
Множество расчетных точек сетки S h
должно быть «связное», т.е. любые две
расчетные точки можно соединить цепочкой узлов, каждые два смежных элемента
которой являются соседними узлами.
110.
РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ МЕТОДОМ СЕТОКЗначение искомой функции u u x, y в точках xi , y j обозначим
Для каждой внутренней точки xi , y j сетки
uij u xi , y j
.
Sh
заменим дифференциальное уравнение (64) конечно-разностным уравнением
uij
В граничных узлах первого рода
1
ui 1 j ui 1 j uij 1 uij 1
4
Bh
сетки
Sh
(65)
полагаем:
u Bh u B B
где B - ближайшая к
Bh
точка границы .
Система (65) является неоднородной линейной системой. Система (65) всегда
совместна и имеет единственное решение.
Если число узлов сетки велико, то решение системы (65) затруднено. Кроме
того, значения искомой функции в граничных узлах выбрано грубо. Это
заставляет для решения системы прибегать к итерационным методам с
одновременным исправлением граничных значений.
111. КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Какие узлы называются соседними?2. Дайте определение внутренних и граничных узлов.
3. Дайте определение граничных узлов первого и второго рода.
4. Какие узлы сетки называются расчетными точками?
5. Какая функция называется гармонической функцией?
6. Сформулируйте принцип максимума.
7. Как выбирается начальное приближение в граничных узлах первого рода?
8. Как выбирается начальное приближение во внутренних узлах сетки?
9. Запишите итерационные формулы для внутренних узлов.
10. Запишите итерационные формулы для граничных узлов.
11. Запишите условие окончания итерационного процесса.
112. ЛЕКЦИЯ 17
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХЗАДАЧ ДЛЯ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
(метод сеток для уравнений
параболического и гиперболического типа)
113.
МЕТОД СЕТОК ДЛЯ УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПАУравнение теплопроводности для однородного стержня длиной
где u u x, t - температура;
2
u
2 u
a
t
x 2
t
0 x l
:
(66)
- время.
Распределение температуры в начальный момент времени
t 0
:
u x,0 f x
Законы изменения температуры в зависимости от времени на концах стержня
x 0, x l :
u 0, t t
,
u l, t t
Требуется найти распределение температуры
0 x l
в любой момент времени
t
u u x, t
вдоль стержня длиной
. Решим эту задачу методом сеток.
114.
МЕТОД СЕТОК ДЛЯ УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПАРассмотрим пространственно-временную систему координат
В полуполосе
t 0, 0 x l
построим прямоугольную сетку
x, t (Рис.10.4).
x ih, i 0, n, t jk , j 0,1,2,...
t
D
O
l
X
Рис. 10.4
Рис.
10.4
Конечно-разностное уравнение:
uij 1 uij
h2
ui 1 j 2uij ui 1 j
После преобразований получим:
h2
uij 1 ui 1 j 1 2 uij ui 1 j
(68)
(69)
Из формулы (69) видно, что для подсчета значения искомой функции
u x, t
в узловых точках j 1 -го слоя используются уже известные значения этой
функции в трех соседних узловых точках
j
-го слоя.
115.
МЕТОД СЕТОК ДЛЯ УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПАИсходя из начального слоя
t 0
, значения функции u x, t определяются из
начального условия u xi ,0 f xi , i 0, n , и, используя значения функции в
граничных узловых точках, определяемые граничными условиями
u 0, t j t j
,
,
u l, t j t j
по формуле (69) последовательно вычисляются
u xi , ti , u xi , t 2 ,..., i 0, n.
Определение. Конечно-разностная схема называется устойчивой, если малые
погрешности, допущенные в процессе решения, затухают или остаются малыми
при неограниченном увеличении номера текущего слоя. В противном случае
конечно-разностная схема называется неустойчивой.
h
Из рассмотренной конечно-разностной схемы («явной схемы») ясно, что шаги
и
k
неодинаковы и выбор шага
h
накладывает ограничения на выбор шага k .
116.
«Неявная схема»Конечно-разностная схема:
uij 1 uij
h2 S
ui 1 j 1 2uij 1 ui 1 j 1
h2
.
(71)
Для решения СЛАУ (71) применяется метод прогонки.
Суть метода прогонки состоит в том, что сначала вычисляются значения
ui 0 fi
. В прямом ходе на очередном
( j 1)
-м временном слое вычисляются
вспомогательные функции
1
;
2 S
b1 j 1 j 1 Su1 j ;
a1 j 1
aij 1
1
;
2 S ai 1 j 1
bij 1 ai 1 j 1bi 1 j 1 Suij , i 2, n.
В обратном ходе вычисляются значения искомой функции на
слое по формуле
( j 1)
uij 1 aij 1(bij 1 ui 1 j 1 )
Величина
u0 j 1 j 1
является значением искомой функции в точке
- в точке ( x0 , t j 1) .
unj 1 j 1
( xn , t j 1)
,а
117.
МЕТОД СЕТОК ДЛЯ УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПАУравнение свободных колебаний однородной ограниченной струны:
2
2u
2 u
a
t 2
x 2
при начальных условиях:
(72)
u x,0 f x ,
u t x,0 F x , 0 x l
(73)
u 0, t 1 t ,
(74)
и краевых условиях:
u l , t 2 t , 0 t .
Конечно-разностное уравнение:
uij 1 2uij uij 1
При k
h
a
k2
a2
ui 1 j 2uij ui 1 j
h2
(75)
уравнение (75) упрощается и принимает вид:
uij 1 uij 1 ui 1 j ui 1 j
откуда:
uij 1 ui 1 j ui 1 j uij 1, j 0,1,...
(76)
118.
МЕТОД СЕТОК ДЛЯ УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПАИз уравнения (76) видно, что для получения значений
используются значения
u x, t
u x, t
в j 1 -м слое
в двух предыдущих слоях j -м и j 1 -м
(Рис.10.6). Для начала вычислений по формуле (76) необходимо знать
значения u x, t в двух слоях
j 0, j 1.
i, j 1
h
i 1, j
k
k
h
i, j
i 1, j
i, j 1
Рис.10.6.
Начальные условия (73) задают значения u x, t лишь на нулевом слое
j 0
Используя начальные условия (73) ut ( x,0) F ( x) , можно определить значения
u x, t на слое с номером j 1 . Для этого запишем соотношение (74) в
конечно-разностном виде:
ui , 1 ui 0 kFi
ui , 1 ui 0
. Зная значения
Fi
, где
Fi F xi
k
u x, t на слое j 1
. Отсюда находим
, можно начать вычисления.
Краевые условия (74) используются для получения значений
u 0 j , u nj .
.
119. КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Приведите пример дифференциального уравнения параболического типа.2. Как выбираются шаги по оси OX и оси OY для уравнения параболического типа?
3. Дайте определение устойчивой конечно-разностной схемы.
4. При каких значениях конечно-разностная схема будет устойчивой?
5. Чему равна погрешность метода сеток для уравнения параболического типа при
различных значениях ?
6. Запишите итерационную формулу метода сеток для дифференциального уравнения
параболического типа.
7. Изобразите схему метода сеток для дифференциального уравнения параболического
типа.
8. Приведите пример уравнения гиперболического типа.
9. Запишите итерационную формулу метода сеток для дифференциального уравнения
гиперболического типа.
10. Изобразите схему метода сеток для дифференциального уравнения гиперболического
типа.









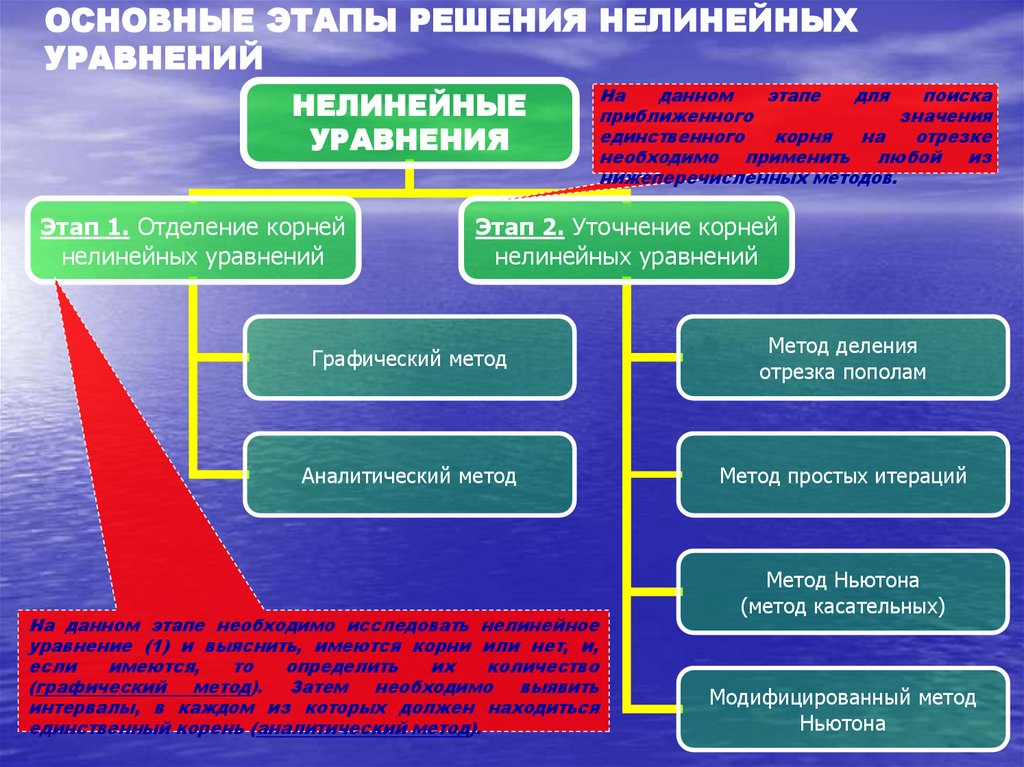
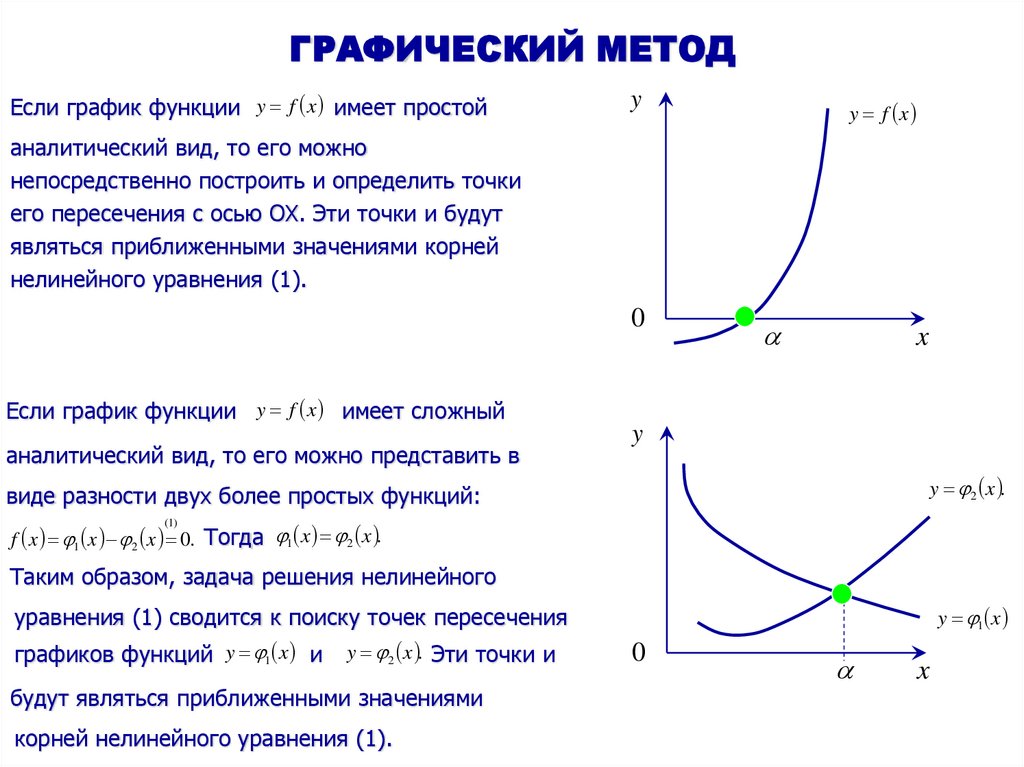


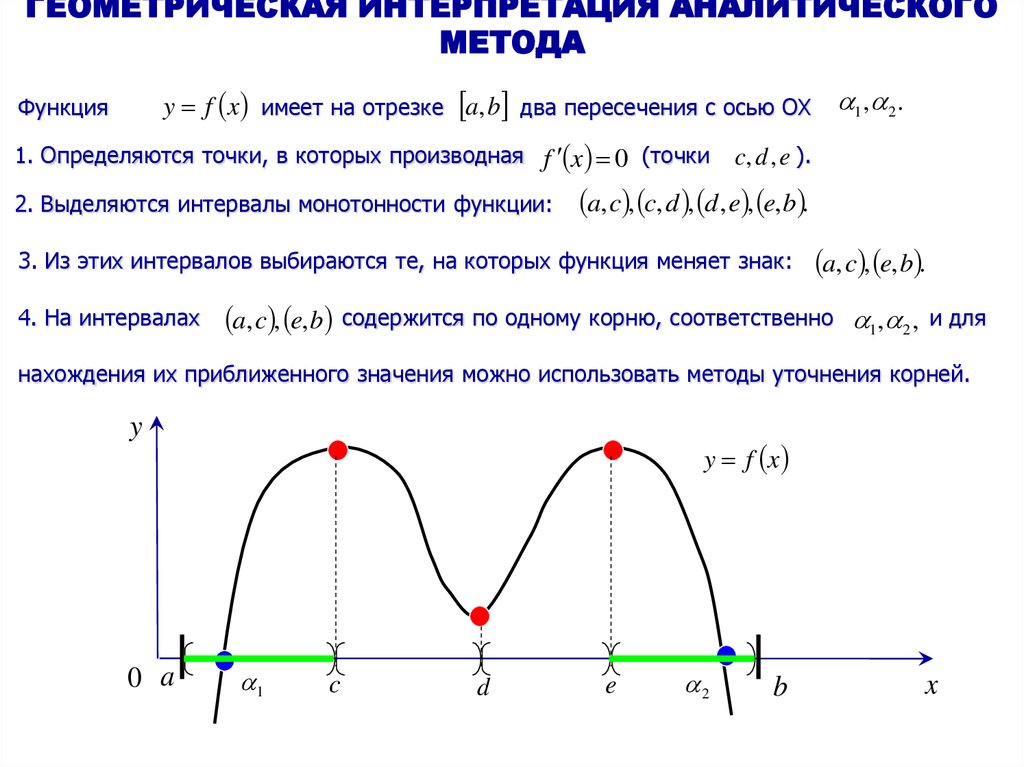

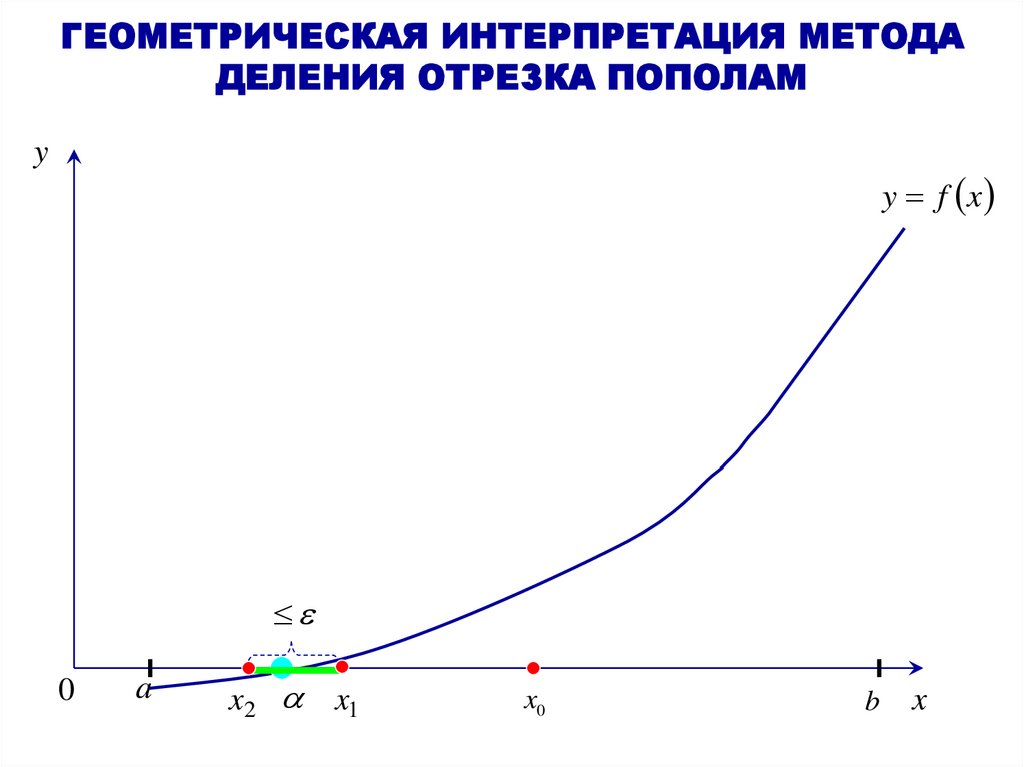




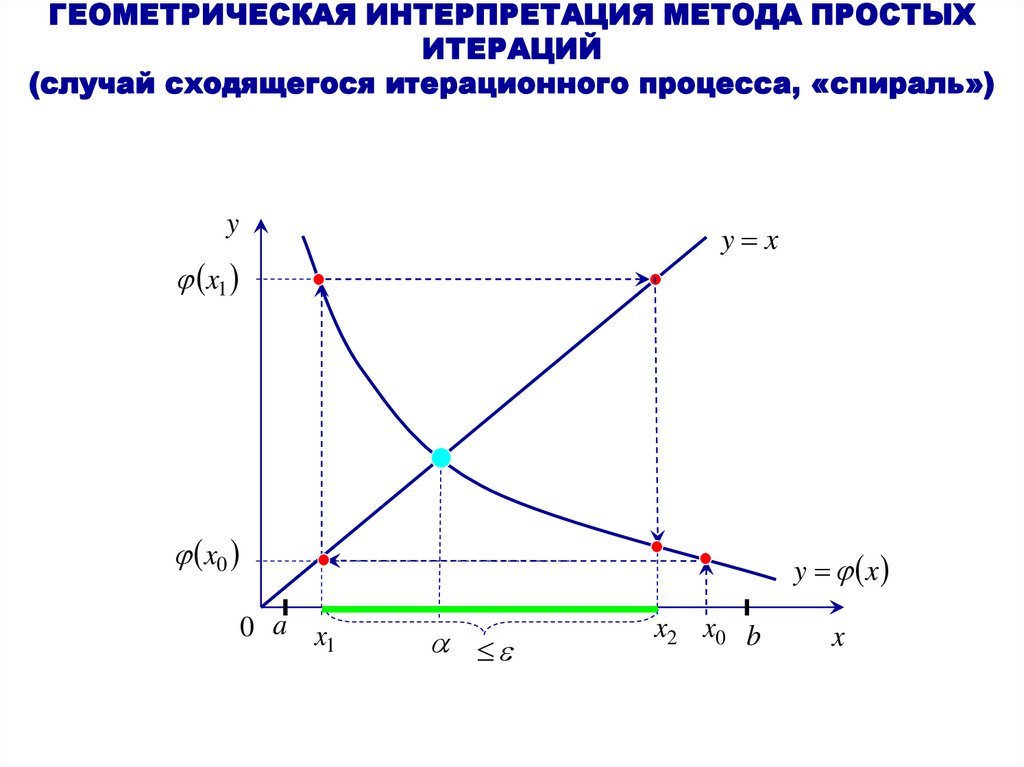
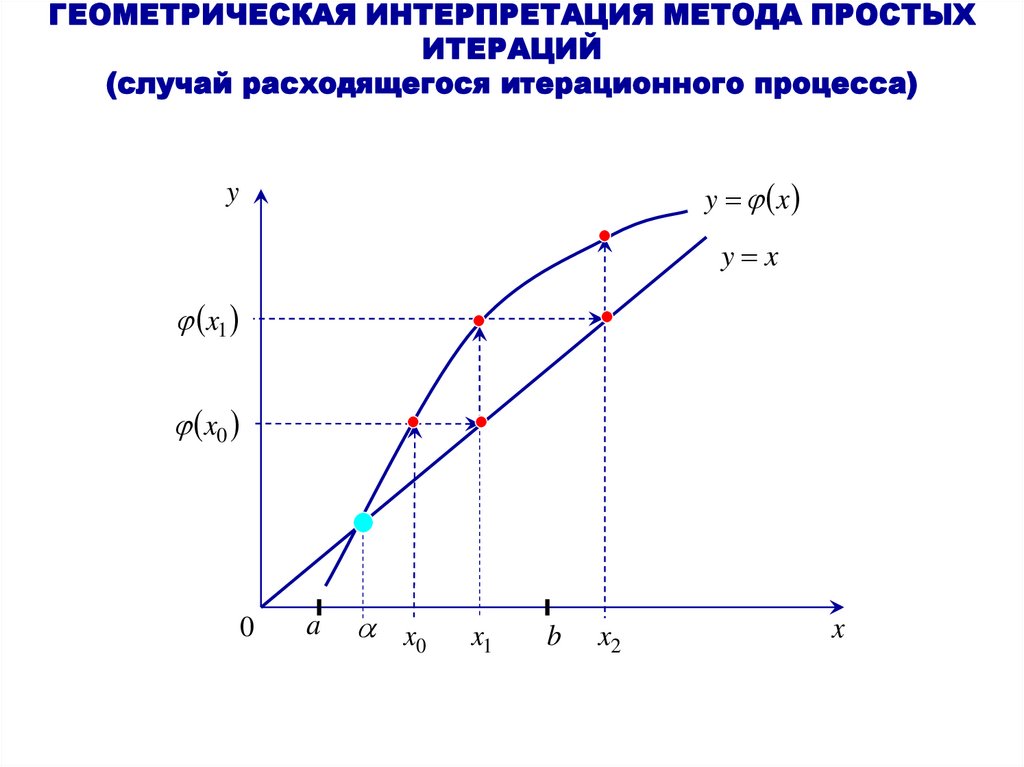



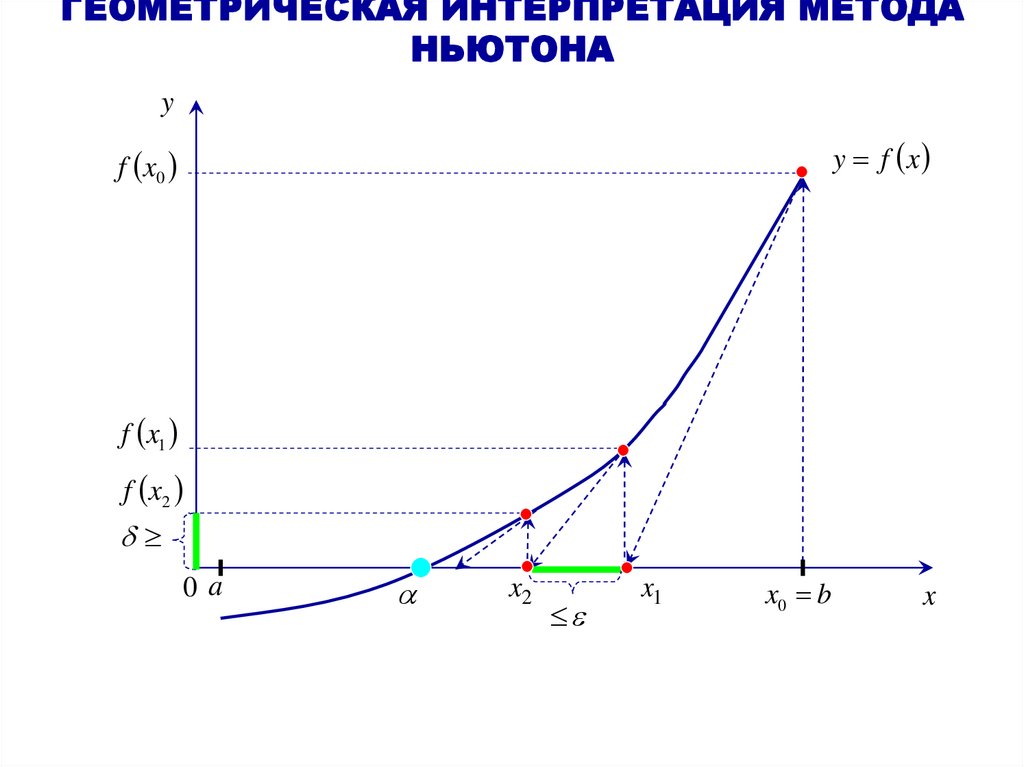

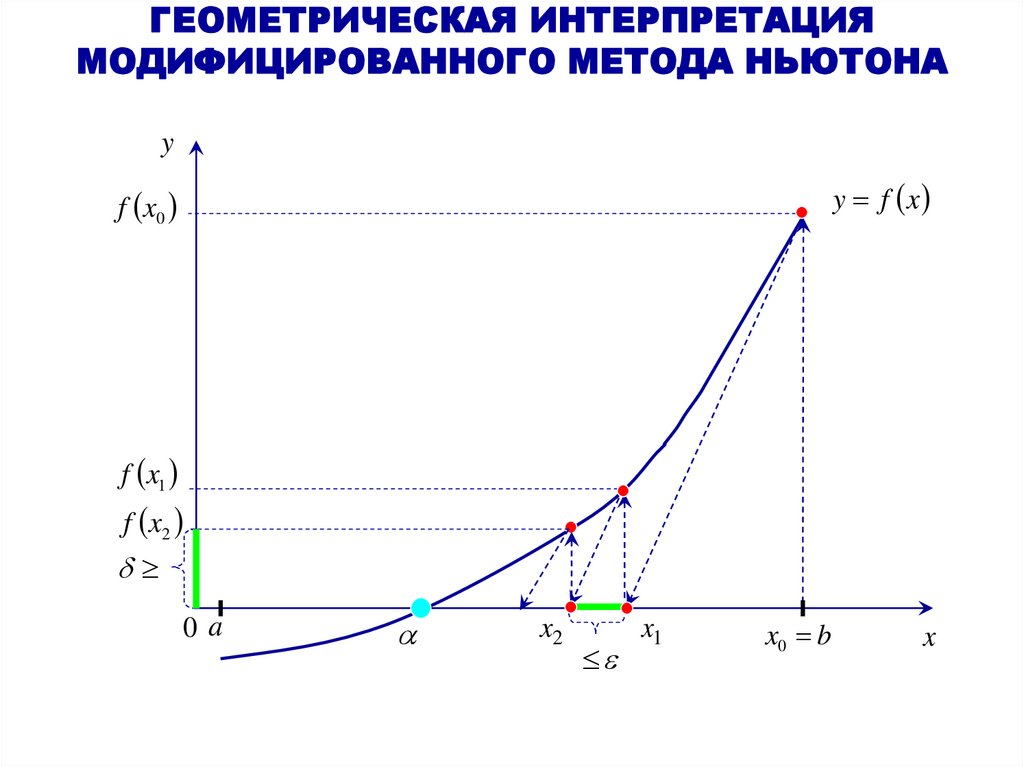



























































































 Математика
Математика








