Геометрическая интерпретация метода простых итераций

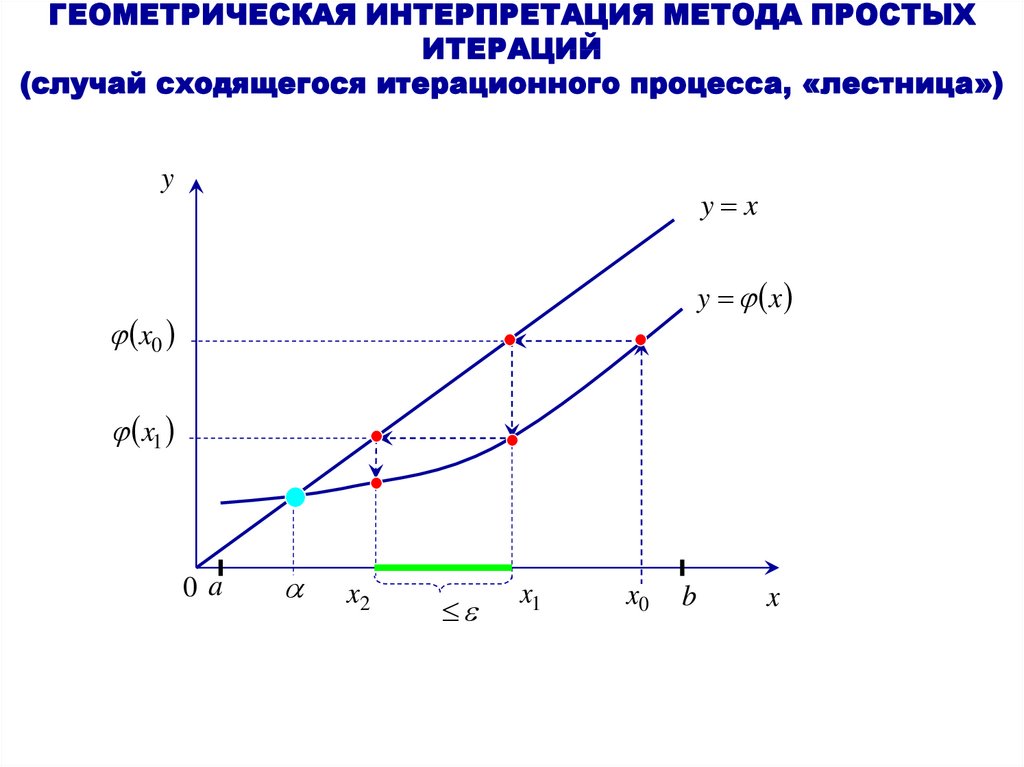
1. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ МЕТОДА ПРОСТЫХ ИТЕРАЦИЙ (случай сходящегося итерационного процесса, «лестница»)

y
y x
y x
x0
x1
0a
x2
x1
x0
b
x

2. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ ДЛЯ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

Пусть дана СНУ (9). Требуется решить ее с заданной точностью
x1 1 x1 , , xn
10
x x , , x
n 1
n
n
1. Приведение системы (9) к эквивалентному виду:
2. Итерационный процесс:
.
x1 k 1 1 x1 k , , xn k
11
x k 1 x k , , x k , k 0,1,...
n 1
n
n
3. Выбор начального приближения: x
0
x1 0 , , xn 0 .
4. Достаточные условия сходимости итерационного процесса (11):
n
i 1
i
1, j 1, n
x j
или
n
j 1
i
1, i 1, n.
x j
5. Условия окончания итерационного процесса (11):
x k 1 x k .
6. Достоинства метода простых итераций: метод является универсальным, самоисправляющимся
и простым для реализации на ЭВМ.
7. Недостатки метода простых итераций:
а) метод обладает медленной скоростью сходимости;
б) метод является трудоемким
n .
2

3. ПЕРВАЯ ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА.

Полагая
x x0
Полагая
x x0
Следовательно:
получим Pn x0 y0 a1h
получим
. Следовательно
Pn x0 y0 2!h a2
2
2
k y0
ak
, k 0, n
k !h k
2
, причем:
a1
y0
h
. Следовательно
2 y0
a2
2!h 2
0! 1, 0 y y
Интерполяционный полином Ньютона:
2
y0
n y0
1 y0
2
Pn x y0
x x0 2 x x0 ... n x x0 n
1!h
2!h
n!h
Для практического использования формулы Ньютона введем новую переменную:
Первый интерполяционный полином Ньютона:
q q 1 2
q q 1 ... q n 1 n
Pn x y0 q y0
y0 ...
y0
2!
n!
При
q
x x0
h
(40)
n 1 получим формулу линейного интерполирования:
Pn x y0 q y0
При n 2
получим формулу квадратичного интерполирования:
q q 1 2
Pn x y0 q y0
y0
2!
Первая интерполяционная формула Ньютона предназначена для интерполирования функции
в окрестности начальной точки.

4. ЛЕКЦИЯ 9

ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ
(формулы численного дифференцирования,
основанные на первой интерполяционной формуле
Ньютона и на интерполяционной формуле
Лагранжа)

5. §6.1. Постановка вопроса.

, заданной таблично, или, в силу сложности аналитического выражения функции
При решении практических задач часто требуется найти производные указанных порядков от
функции y f ( x) , заданной таблично, или, в силу сложности аналитического выражения функции
y f ( x), непосредственное ее дифференцирование затруднено. В этих случаях прибегают к
приближенному дифференцированию.
Для этого на отрезке a, b функцию y f ( x) заменяют интерполирующей функцией F x (чаще
всего интерполирующим полиномом Pn ( x)), затем полагают f ( x) F ( x) при a x b
.
Аналогично поступают при нахождении производных высших порядков от функции
y f ( x) .
Если для интерполирующей функции известна погрешность
то погрешность производной
R x f x F x
r x f x F x R x ,
т.е. погрешность производной интерполирующей функции равна производной от погрешности
этой функции. То же справедливо для производных высших порядков.
Приближенное дифференцирование является менее точной операцией, чем интерполирование.
Близость друг к другу ординат двух кривых y f x и Y F x на отрезке
a, b
еще не
гарантирует близости на этом отрезке их производных f x и F x , то есть малого
расхождения угловых коэффициентов касательных к рассматриваемым кривым при одинаковых
значениях аргумента.

6. §6.2. Формулы приближенного дифференцирования, основанные на первой интерполяционной формуле Ньютона.

b a
Пусть на отрезке a, b заданы равноотстоящие точки xi : xi x0 ih, i 0, n, h
,и
n
известны значения функции в этих точках yi f xi , i 0, n. Требуется найти производные
f x , f x ,... на отрезке a, b (заранее известно, что эти производные существуют).
Заменим функцию y f x интерполяционным полиномом Ньютона, построенным для узлов
xi , i 0, n воспользовавшись первой интерполяционной формулой Ньютона:
q q 1 2
q q 1 q 2 3
y0
y0
2!
3!
q q 1 q n 1 n
q q 1 q 2 q 3 4
y0
y0 ,
4!
n!
y x Pn x y0 q y0
где q
(6.1)
x x0
.
h
Произведя перемножение биномов и приведя подобные, получим:
q2 q 2
q3 3q 2 2q 3
q 4 6q3 11q 2 6q 4
y x y0 q y0
y0
y0
y0
2!
3!
4!
(6.2)
Так как
dy dy dq 1 dy
,
dx dq dx h dq
то
y x
1 2
6q 2 18q 11 4
3
y
q
1
y
y0
0
0
h 2
12
.
(6.4)

7.

Таким образом можно вычислить производную любого порядка.
При нахождении производных f x , f x ,... в фиксированной точке x
следует брать ближайшее к x
в качестве x0
табличное значение аргумента.
Формулы (6.3) и (6.4) упрощаются, если нужно подсчитать производные в узлах
интерполяции. Полагая x x0, q 0, получаем:
y x
1
1
1
1
y0 2 y0 3 y0 4 y0
h
2
3
4
y x
1 2
11
y0 3 y0 4 y0
2
h
12
(6.5)
(6.6)
Пусть Pn x - интерполяционный полином Ньютона, содержащий конечные разности
y0 , 2 y0 ,..., n y0 и Rn x f x Pn x , тогда Rn x f x Pn x .
Но Rn x hn 1
q q 1 ... q n n 1
y
. Тогда, если y x C n 2 , то
n 1 !
dRn dq
hn
Rn x
dq dx n 1 !
n 1
n 1
dy
d
y
q q 1 ... q n q q 1 ... q n
.
dq
dq
(6.7)

8.

Полагая
dy
n 1
dq
- ограниченной и учитывая, что
d
q q 1 ... q n
dq
1 n! ,
n
q 0
получаем при x x0, q 0 :
h n n! n 1
h n n 1
n
Rn x0 1
y 1
y
n 1
n 1 !
(6.8)
n
Так как y
n 1
сложно определить, то при малом шаге h принято считать y
n 1
n 1 y0
n 1 .
h
Тогда (6.8) примет вид:
hn n 1 y0 1 n 1 y0
Rn x0 1
n 1 hn 1
h
n 1
n
n
Аналогично находится Rn x0 и так далее.
Формулы приближенного дифференцирования аналогичным образом можно получить,
используя вторую интерполяционную формулу Ньютона.
(6.9)

9. §6.3. Формулы численного дифференцирования для равноотстоящих точек, основанные на интерполяционной формуле Лагранжа.

Пусть даны равноотстоящие точки xi , i 0, n такие, что xi x0 ih, i 0, n, и известны значения
функции в этих точках yi f xi , i 0, n , и известны значения функции в этих точках
yi f xi , i 0, n .
Для данной системы узлов yi f xi построим интерполяционный полином Лагранжа:
n
Ln x yi
i 0
x x0 ... x xi 1 x xi 1 ... x xn n n 1 x yi ,
xi x0 ... xi xi 1 xi xi 1 ... xi xn
i 0 x xi n 1 xi
(6.10)
где n 1 x x x0 ... x xi ... x xn .
Для Ln x справедливо соотношение
Введем новую переменную q
Ln xi yi .
x x0
, тогда
h
n 1 x hn 1 q q 1 ... q n hn 1q
n 1
n 1 xi xi x0 ... xi xi 1 xi xi 1 ... xi xn
h n i i 1 ...1 1 ... n i 1
Подставив (6.11), (6.12) в (6.10), получим:
n i
h n i ! n i !
(6.11)
(6.12)

10.

1 yi q n 1
Ln x
i
!
n
i
!
q i
i 0
n
n i
(6.13)
Заменив функцию y x интерполяционным полиномом Лагранжа Ln x , и, учитывая, что
dLn x dLn x dq 1 dLn x из соотношения (6.13) получим:
dx
dq
dx h
dq
n i
n 1
1 n 1 yi d q
(6.14)
y x Ln x
h i 0 i ! n i ! dq q i
Аналогично можно найти y x и так далее.
Для оценки погрешности
rn x y x L x Rn x воспользуемся формулой погрешности
интерполяционной формулы Лагранжа:
y
Rn x y x Ln x
x
n 1 ! n 1 ,
n 1
где - промежуточное значение между x и узлами интерполяции x0 , x1 ,..., xn .
Предположим, что y x C
n 2
, тогда
n 1
dy x
1
n 1
rn x Rn x
y n 1 x n 1 x
dx
n 1 !
Учитывая соотношение (6.12) и предполагая
dy
n 1
dx
(6.15) получим оценку погрешности в узлах интерполяции:
rn xi 1
n i
hn
(6.15)
- ограниченной, из соотношения (6.15)
i ! n i ! n 1
y
n 1 !

11. ЛЕКЦИЯ 10

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
(квадратурная формула Ньютона-Котеса,
частные случаи формулы Ньютона-Котеса
(формула трапеций, формула Симпсона))

12. §7.1. Квадратурная формула Ньютона-Котеса.

Если функция f x непрерывна на отрезке a, b и известна ее первообразная F x , то
определенный интеграл от этой функции в пределах от a до b может быть вычислен по формуле
Ньютона-Лейбница:
b
f x dx F b F a
(7.1)
a
Однако, во многих случаях первообразная F x не может быть найдена с помощью
элементарных средств или является слишком сложной; вследствие этого вычисление
определенного интеграла по формуле (7.1) может быть затруднено или быть практически
невыполнимым. Кроме того, подынтегральная функция f x часто задается таблично и тогда само
понятие первообразной теряет смысл. Поэтому, важное значение приобретают численные методы
вычисления определенных интегралов, использующие ряд значений подынтегральной функции в
точках xi a, b , где i 0, n .
Определение 7.1.
Численное вычисление однократного интеграла называется механической квадратурой,
двойного интеграла - механической кубатурой. Соответствующие формулы называются
квадратурными и кубатурными формулами.
Рассмотрим один из способов вычисления определенных интегралов.
Если воспользоваться, например, интерполяционным полиномом Лагранжа, то, заменяя

13.

функцию f x полиномом Ln x , получим равенство
b
b
a
a
f x dx L x dx R f ,
n
где Rn f - ошибка этой интерполяционной формулы.
b
Требуется вычислить интеграл
(7.2)
n
b a
, разобьем отрезок
n
x0 a , xi x0 ih , i 1, n 1 , xn b ,
ydx, где y f x . Выбрав шаг
a
a, b на n равных частей с помощью равноотстоящих точек
yi f xi , i 0, n . Заменим подынтегральную функцию
y f x
h
интерполяционным полиномом
n
Лагранжа Ln x ai x yi и получим приближенную квадратурную формулу
i 0
b
b
b
xn n
a
a
x0 i 0
f x dx ydx Ln x dx
a
? n
ai x yi dx Ai yi
i 0
,
(7.3)
где Ai - некоторые постоянные коэффициенты.
Выведем явные выражения для коэффициентов Ai формулы (7.3). Многочлен Лагранжа
n
Ln x ai x yi имеет коэффициенты
i 0
x x0 x x1
ai x
xi x0 xi x1
x xi 1 x xi 1 x xn , i 0, n.
xi xi 1 xi xi 1 xi xn
x x0
n 1
и q q q 1
h
многочлен Лагранжа запишем в виде:
Введем обозначения
q
q n
n 1
1
q
Ln x
yi
i
!
n
i
!
q
i
i 0
n
n i
и с учетом этих обозначений
(7.4)

14.

Заменяя в (7.3) функцию f x полиномом Ln x по формуле (7.4), получим:
1 q n 1 y dx n A y
i
i i,
x
i 0 i ! n i ! q i
i 0
n i
xn n
0
n 1
1
q
Ai
dx .
i ! n i ! q i
x
xn
где
n i
0
Так как q
иметь:
dx
x x0
и dq
, то сделав замену переменных в определенном интеграле, будем
h
h
n n 1
1
q
Ai h
dq, i 0, n
i ! n i ! 0 q i
n i
Так как Ai b a H i , где коэффициенты
n n 1
1 1
q
Hi
dq, i 0, n
n i ! n i ! 0 q i
n i
(7.5)
называются коэффициентами Котеса, то можно записать следующую квадратурную формулу:
b
n
a
i 0
ydx b a H i yi
Формула (7.6) называется квадратурной формулой Ньютона-Котеса.
Нетрудно проверить, что для коэффициентов Котеса справедливы соотношения:
n
1) H i 1 ;
i 0
2) H i H n i .
(7.6)

15. §7.2. Частные случаи квадратурной формулы Ньютона-Котеса.

7.2.1. Формула трапеций.
а) Пусть отрезок
a, b
достаточно мал. Положим h b a . Тогда по формуле (7.5) при n 1
вычислим:
1
H 0 q 1 dq
0
1
H1 qdq
0
x1
h
ydx 2 y
0
1
,
2
1
,
2
y1 .
(7.7)
x0
Полученная формула (7.7) называется формулой трапеций для приближенного вычисления
определенного интеграла (Рис.7.1).
y
y f x
R
y0
y1
h
0
x0
Рис.7.1
Погрешность квадратурной формулы (7.7)Рис.7.1
равна:
x1
x

16.

x1
h
h3
R ydx y0 y1 y , где x0 , x1 .
2
12
x0
(7.8)
Если y 0 то формула (7.7) дает значение интеграла с избытком, если y 0
- то с недостатком.
б) Рассмотрим общий случай, когда отрезок a, b произвольной длины.
Разделим отрезок a, b на n равных частей x0 , x1 , x1 , x2 , …, xn 1 , xn и к каждому из них
применим формулу трапеций. Получим:
b
x1
x2
xn
x0
x1
xn 1
ydx ydx ydx ...
a
ydx
h
h
h
y0 y1 y1 y2 ... yn 1 yn
2
2
2
y
y
h 0 y1 y2 ... yn 1 n ,
2
2
где
h
(7.9)
b a .
n
Формула (7.9) называется общей формулой трапеций. Для нее справедлива оценка
погрешности:
h3 n
nh3
b a h2 y
R y i
y
,
12 i 1
12
12
1 n
где i xi 1, xi , y y i , a, b .
n i 1
(7.10)

17. 7.2.2. Квадратурная формула Симпсона.

а) По формуле (7.5) при n 2 вычислим коэффициенты Котеса:
2
1 1
1
H 0 q 1 q 2 dq ,
2 20
6
2
1 1
2
H1 q q 2 dq ,
2 10
3
2
1 1
1
H 2 q q 1 dq .
2 20
6
Так как x2 x0 2h , то квадратурная формула для вычисления интеграла примет вид
x2
h
ydx 3 y
0
4 y1 y2
(7.11)
x0
Формула (7.11) называется квадратурной формулой Симпсона. Геометрическая
интерпретация формулы состоит в том, что происходит замена данной кривой y f x параболой
y L2 x , проходящей через три точки M 0 x0 , y0 , M1 x1, y1 , M 2 x2 , y2 (Рис.7.2).

18.

y f x
y
M1
y L2 x
R
R
M2
M0
y2
y1
y0
h
0
x0
h
x1
x2
x
Рис.7.2
Погрешность квадратурной формулы Симпсона равна:
R
x2
x0
ydx
h
h5 IV
y
4
y
y
y , где x0 , x2 .
0
1
2
3
90
(7.12)
Квадратурная формула Симпсона является точной для полиномов второй и третьей степени.
б) Общая формула Симпсона.
Пусть n 2m - четное число, и yi f xi - значения функции y f x для равноотстоящих
b a
точек xi x0 ih с шагом h
, i 0,2m .
2m
Применяя квадратурную формулу Симпсона (7.11) к каждому сдвоенному промежутку
x0 , x2 , x2 , x4 , … x2m 2 , x2m
длины 2h , будем иметь:

19.

b
x2
x4
x2 m
x0
x2
x2 m 2
ydx ydx ydx ...
a
ydx
h
h
y0 4 y1 y2 y2 4 y3 y4 ...
3
3
h
y2 m 2 4 y2 m 1 y2 m .
3
Отсюда получим общую квадратурную формулу Симпсона:
b
ydx
a
h
y0 y2 m 4 y1 y3 ... y2 m 1 2 y2 y4 ... y2 m 2
3
(7.13)
Остаточный член формулы (7.13) равен:
h5 m IV
R y k .
90 k 1
В силу непрерывности y IV x на отрезке a, b найдется точка a, b , такая, что
1 m IV
y y k .
m k 1
IV
Поэтому будем иметь:
mh5 IV
b a h y IV
R
y
,
90
180
4
где a, b .
(7.14)

20. §7.3. Квадратурная формула Гаусса.

21. ЛЕКЦИЯ 11

ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ
ФУНКЦИЙ
(приближенное вычисление несобственных
интегралов)

22. §7.4. Приближенное вычисление несобственных интегралов.

Определение 7.3.
Интеграл
b
f x dx
(7.22)
a
называется собственным, если
1.
промежуток интегрирования a, b конечен;
2.
подынтегральная функция f x непрерывна на a, b .
В противном случае, интеграл (7.22) называется несобственным.
а) Рассмотрим приближенное вычисление несобственного интеграла
f x dx
(7.23)
a
с бесконечным промежутком интегрирования, где функция f x непрерывна при a x .
Определение 7.4.
Интеграл (7.23) называется сходящимся (Рис.7.3), если существует конечный предел
b
lim f ( x)dx
b
a
(7.24)

23.

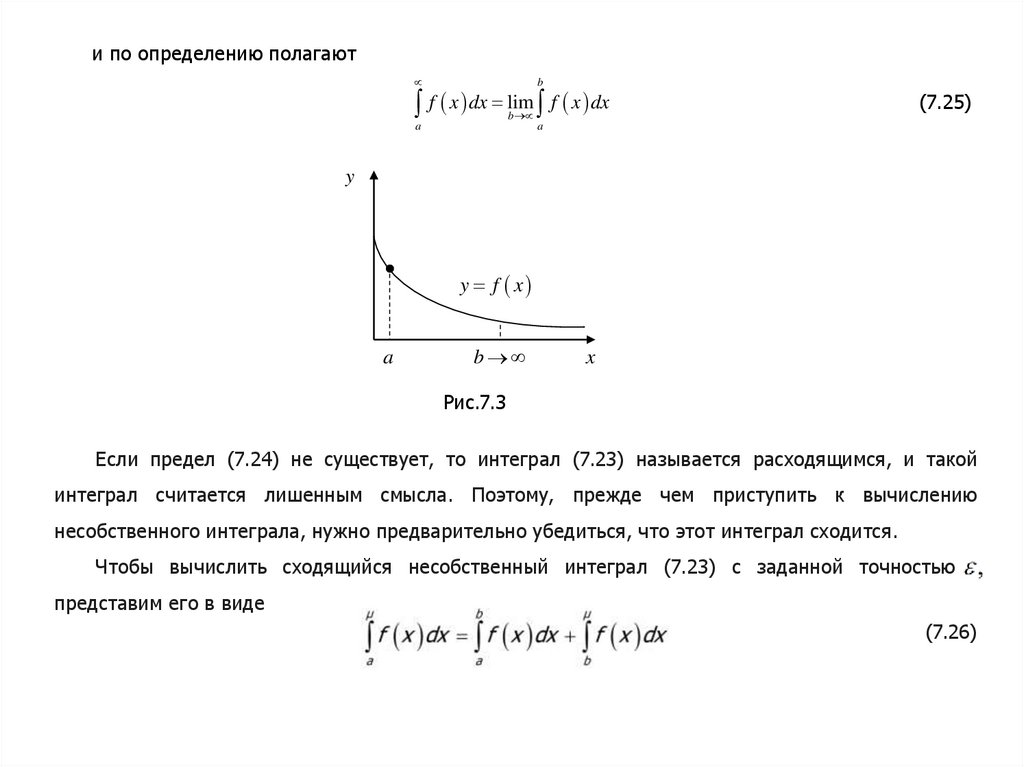
и по определению полагают
b
f x dx lim f x dx
b
a
(7.25)
a
y
y f x
a
b
Текст слайда
x
Рис.7.3
Если предел (7.24) не существует, то интеграл (7.23) называется расходящимся, и такой
интеграл считается лишенным смысла. Поэтому, прежде чем приступить к вычислению
несобственного интеграла, нужно предварительно убедиться, что этот интеграл сходится.
Чтобы вычислить сходящийся несобственный интеграл (7.23) с заданной точностью ,
представим его в виде
(7.26)

24.

В силу сходимости интеграла число b можно выбрать столь большим, чтобы имело место
неравенство
(7.27)
Собственный интеграл
можно вычислить по одной из квадратурных формул.
Пусть S - приближенное значение этого интеграла с точностью до
, т.е.
(7.28)
Из формул (7.26) - (7.28) имеем
,,
т.е. поставленная задача решена.
б) Допустим теперь, что отрезок [a,b] конечен, а функция f(x) имеет конечное число точек
разрыва на [a,b]. Эти точки назовем «особыми» и обозначим
. Такими особыми
точками могут быть или один из концов отрезка, или оба конца отрезка, либо одна или
несколько точек внутри отрезка.
Так как промежуток интегрирования можно разбить на частичные промежутки с
единственной точкой разрыва подынтегральной функции, то достаточно разобрать лишь
случай, когда на [a,b] имеется единственная точка разрыва c функции y=f(x), причем второго
рода.

25.

Если c есть внутренняя точка отрезка [a,b], то по определению полагают:
(7.29)
и в случае существования этого предела интеграл называют сходящимся, в противном
случае – расходящимся.
Аналогично определяется сходимость несобственного интеграла, если точка разрыва
c подынтегральной функции f(x) совпадает с одним из концов промежутка интегрирования.
Для приближенного вычисления с заданной точностью
интеграла (7.29), где точка разрыва
сходящегося несобственного
, выбирают положительные числа
и
столь
малыми, чтобы имело место неравенство:
Текст слайда
….......
Затем
по
интегралы
с точностью
известным
квадратурным
формулам
, с точностью до
, т.е.
вычисляют
. Тогда
определенные
с

26.

Если точка разрыва c подынтегральной функции y=f(x) является концевой для промежутка
интегрирования [a,b], то методика вычисления очевидным образом видоизменяется.
§7.5. Кубатурные формулы типа Симпсона.
Рассмотрим один из методов приближенного вычисления двойного интеграла.
Так как двойной интеграл вычисляется через повторный, то при приближенном
вычислении двойного интеграла используется квадратурная формула Симпсона.
1) Вычислим
, где область D – это прямоугольник вида:
Каждый отрезок [a,A], [b,B] разобьем пополам точками
где
Получим девять точек с координатами
(Рис.7.4).

27.

Рис.7.4
Расписав двойной интеграл через повторный и применив два раза квадратурную формулу
Симпсона, получим:
(7.30)
Формула (7.30) называется кубатурной формулой Симпсона.
Текст слайда

28.

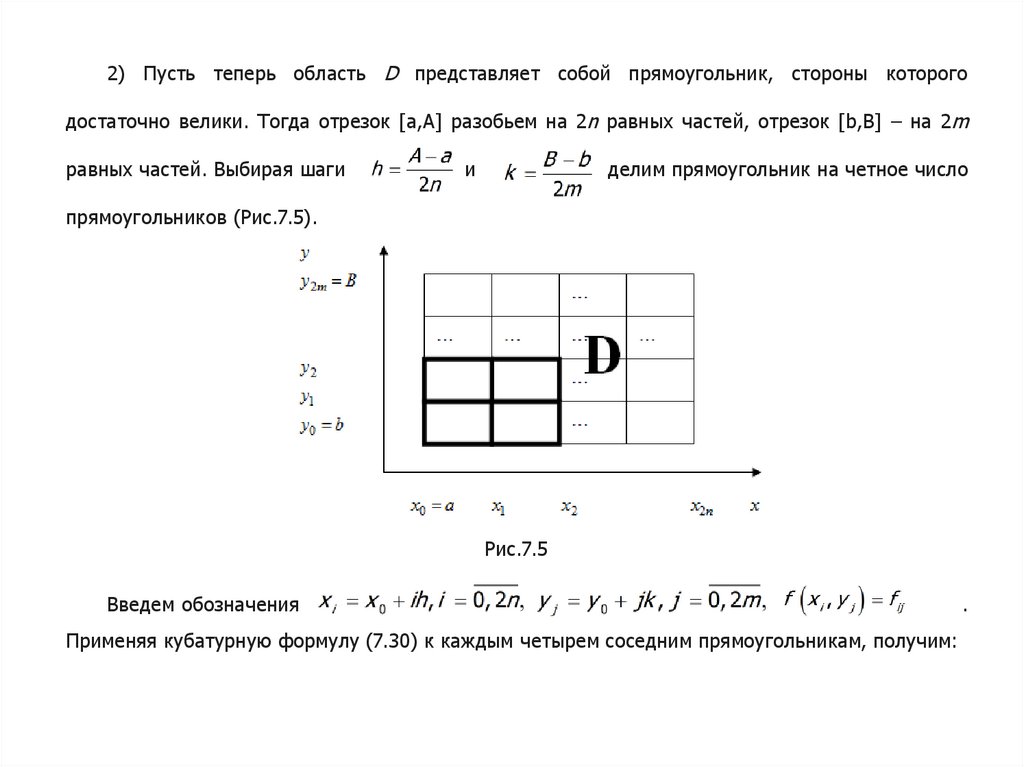
2) Пусть теперь область D представляет собой прямоугольник, стороны которого
достаточно велики. Тогда отрезок [a,A] разобьем на 2n равных частей, отрезок [b,B] – на 2m
равных частей. Выбирая шаги
и
, делим прямоугольник на четное число
прямоугольников (Рис.7.5).
Рис.7.5
Введем обозначения
Применяя кубатурную формулу (7.30) к каждым четырем соседним прямоугольникам, получим:
.

29.

Приведя подобные, получим:
(7.31)
где коэффициенты
являются соответствующими элементами матрицы
.
3) Если область D – произвольная криволинейная область, то строится прямоугольник
содержащий область D, причем стороны прямоугольника
(Рис.7.6).
,
параллельны осям координат

30.

Рис.7.6
Рассматривается вспомогательная функция
.
Тогда
и, применяя к последнему интегралу общую
кубатурную формулу Симпсона (7.31), получим приближенное значение двойного интеграла
по произвольной области

31. КУБАТУРНЫЕ ФОРМУЛЫ ТИПА СИМПСОНА

z
z f x, y
0
a
x
b
B
y
A
D

32. ЛЕКЦИЯ 12

ПРИБЛИЖНОЕ ИНТЕГРИРОВАНИЕ
ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ И СИСТЕМ
(методы Эйлера, Рунге-Кутта и Адамса)

33.

Дифференциальные
уравнения
являются
основным
математическим
инструментом
моделирования и анализа разнообразных явлений и процессов в науке и технике.
Методы их решения подразделяются на два класса:
аналитические методы, в которых решение получается в виде аналитических функций;
численные (приближенные) методы, где искомые интегральные кривые получают в виде
таблиц их численных значений.
Применение аналитических методов позволяет исследовать полученные решения методами
математического анализа и сделать соответствующие выводы о свойствах моделируемого
явления или процесса. К сожалению, с помощью таких методов можно решать достаточно
ограниченный круг реальных задач. Численные методы позволяют получить с определенной
точностью приближенное решение практически любой задачи.
Решить дифференциальное уравнение
(7.1)
численным методом означает, что для заданной последовательности аргументов
и
y=F(x), найти значения
числа
, не определяя аналитического вида функции
, удовлетворяющие условиям:

34.

Рассмотрим три наиболее распространенных при решении практических задач численных
метода интегрирования Эйлера, Рунге-Кутта и Адамса.
§8.1. Метод Эйлера.
Этот метод является сравнительно грубым и применяется в основном для ориентировочных
расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда
других численных методов.
Пусть дано дифференциальное уравнение с начальными условиями (задача Коши)
(7.2)
и выполняются условия существования и единственности решения.
Теорема Пиккара (теорема о существовании и единственности решения задачи Коши).
Если
в
уравнении
(7.1)
функция
f(x,y)
непрерывна
в
прямоугольнике
и удовлетворяет в D условию Липшица
где N - константа Липшица, то существует единственное решение
уравнения (7.1), удовлетворяющее условию
в D.

35.

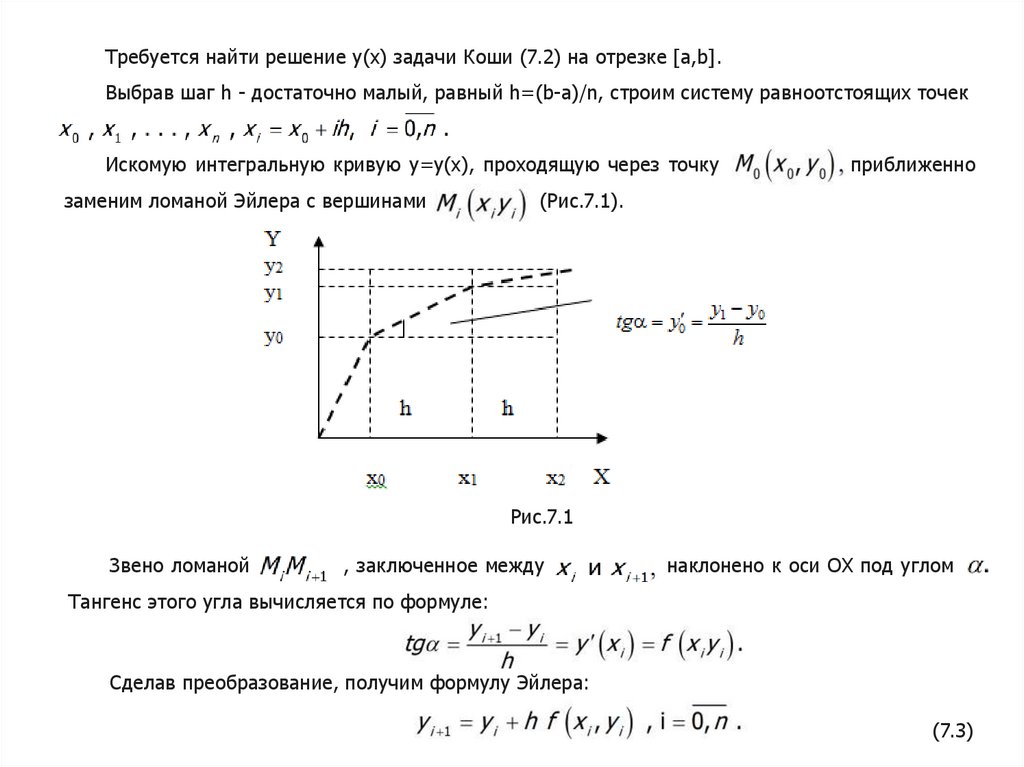
Требуется найти решение y(x) задачи Коши (7.2) на отрезке [a,b].
Выбрав шаг h - достаточно малый, равный h=(b-a)/n, строим систему равноотстоящих точек
Искомую интегральную кривую y=y(x), проходящую через точку
заменим ломаной Эйлера с вершинами
приближенно
(Рис.7.1).
Рис.7.1
Звено ломаной
, заключенное между
наклонено к оси ОХ под углом .
Тангенс этого угла вычисляется по формуле:
Сделав преобразование, получим формулу Эйлера:
(7.3)

36.

Вычисление значений
осуществляется с использованием формулы (7.3)
следующим образом. По заданным начальным условиям
полагая i=0 в выражении
(7.3) вычисляется значение
(7.4)
Далее определяя значение аргумента x по формуле
значение
и полагая в формуле (7.3)
, используя найденное
вычисляем следующее приближенное значение
интегральной кривой , как
(7.5)
Поступая аналогичным образом при
определяем все остальные значения
том числе последнее значение
в
которое соответствует значению
аргумента
Таким образом, соединяя на координатной плоскости точки
отрезками прямых в качестве приближенного представления искомой интегральной кривой
y=F(x), получаем ломанную линию с вершинами в точках
Метод Эйлера может быть применен к решению систем дифференциальных уравнений.
Пусть задана система двух уравнений первого порядка

37.

(7.6)
с начальными условиями
Необходимо найти решение этой задачи Коши. Проводя аналогичные рассуждения, получаем
расчетные формулы вида:
(7.7)
где h - шаг интегрирования.
При расчетах полагается, что
схемы
(7.7)
получается
приближенное
В результате применения расчетной
представление
интегральных
кривых
в форме двух ломаных Эйлера, построенных по полученным таблицам
Запишем разложение
в ряд Тейлора:
(7.8)

38.

Учитывая формулы (7.3) и (7.8), получим
(7.9)
Соотношение (7.9) может быть использовано для выбора шага h. Как правило, шаг h
выбирают таким образом, чтобы
, где
- заданная точность.
Достоинством метода Эйлера является его простота и высокая скорость поиска решения.
Недостатком метода Эйлера является малая точность.
§8.2. Метод Рунге-Кутта.
Данный метод является одним из наиболее распространенных численных методов
интегрирования обыкновенных дифференциальных уравнений. По сравнению с описанным
выше методом Эйлера метод Рунге-Кутта имеет более высокую точность, но невысокую
скорость поиска решения, так как метод относится к классу многошаговых методов.