Комплексные числа

1.

Комплексные
числа
Работа ученика 11 «Б» класса
Алиева Парвина Натиговича
Руководитель проекта
Сим Татьяна Александровна
Учитель математики

2.

Введение
Решая квадратные уравнения, школьники иногда встречаются с
проблемой отрицательного значения дискриминанта. Из школьного
курса математики известно, что квадратное уравнение с
отрицательным дискриминантом корней не имеет.
Однако, как оказалось, способ все же есть. Нет решений только в
действительных числах, на самом же деле, найти корни любого
квадратного уравнения представляется возможным в случае
применения знаний о комплексных числах. Открытие комплексных
чисел стало важным шагом в развитии математики. Алгебра
комплексных чисел используется при точном прогнозировании
многочисленных процессов современной науки и техники.
В своем проекте я хочу рассказать о комплексных числах, так как
данная тема актуальна из-за того, что их описания нет в школьном
курсе математики, а многим современным новаторским индустриям в
перспективе окажутся необходимы знания комплексных чисел.

3.

Цель: познакомиться с комплексными числами
и их применением в математике.
Задачи:
Изучить историю возникновения комплексных чисел;
Раскрыть суть комплексного числа;
Проанализировать
действия
над
комплексными
числами;
Разработать памятку «Комплексные числа».

4.

Проблема: отсутствие темы комплексных чисел в школьной
программе и неспособность школьников решения квадратных
уравнений с отрицательным значением дискриминанта.
Объект исследования: разнообразные формы комплексного
числа и действия над ними.
Предмет исследования: комплексные числа.
Гипотеза: изучение раздела о комплексных числах позволит
увеличить уровень математической грамотности и в
перспективе внедрить свои знания в область
Проектный продукт: Памятка «Комплексные числа».
Методы исследования: анализ литературных источников,
обобщение результатов.

5.

Рафаэль Бомбелли

6.

Иоганн Гаусс

7.

Джероламо Кардано

8.

Леонард Эйлер

9.

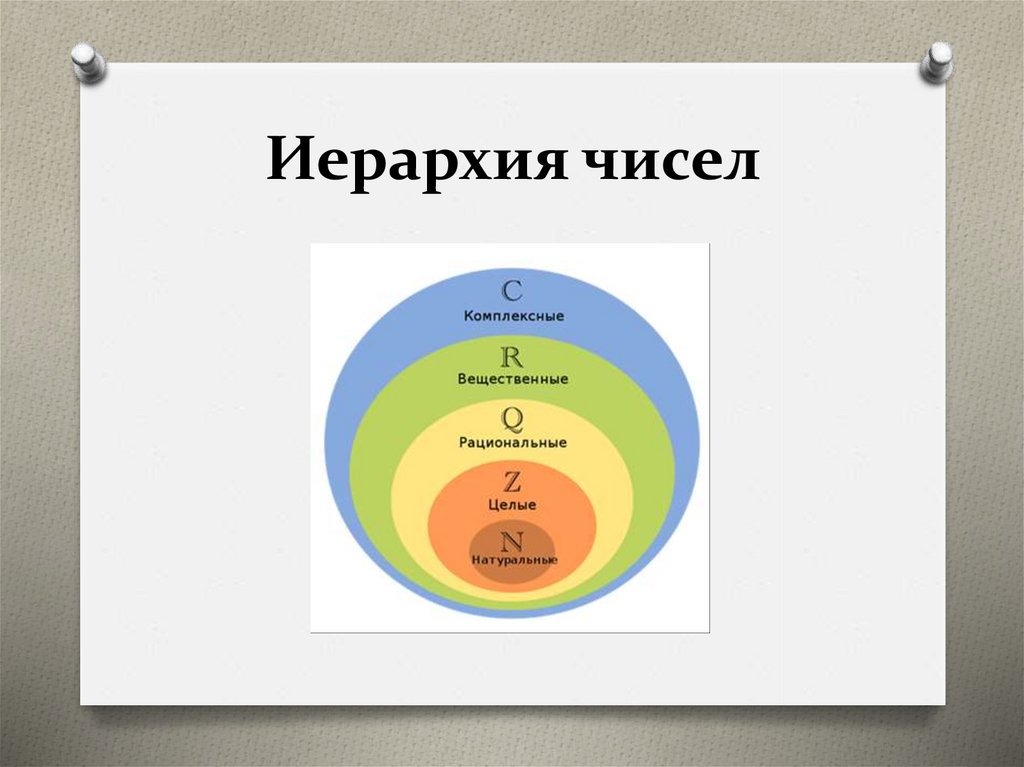
Иерархия чисел

10.

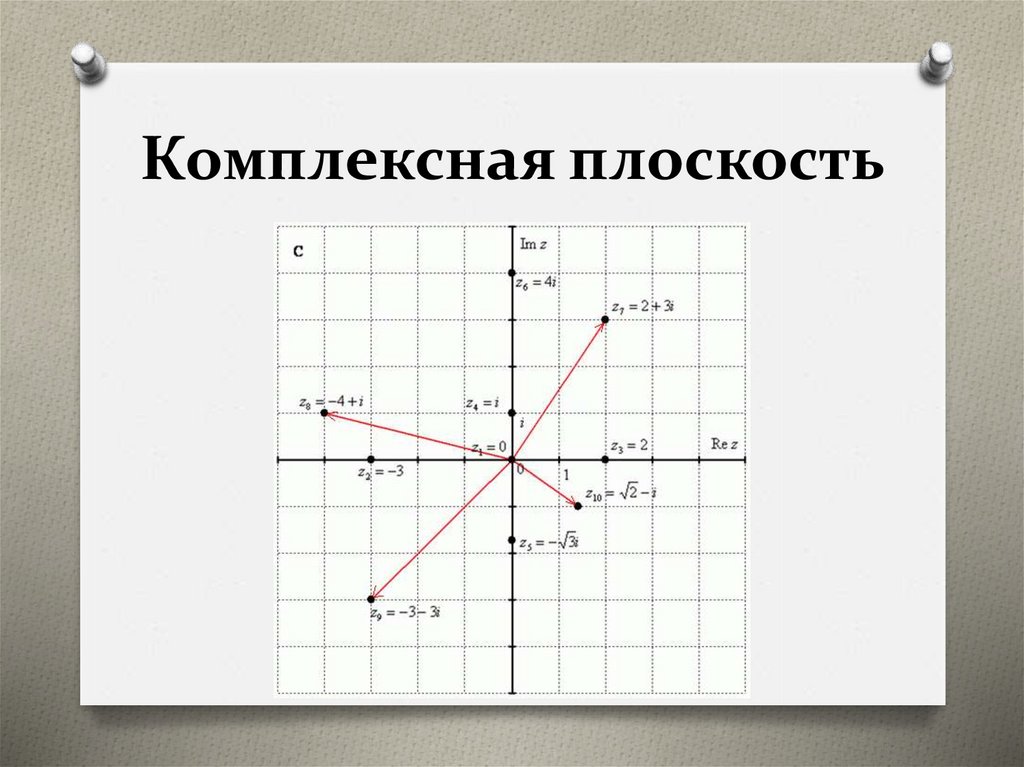
Комплексная плоскость

11.

Сложение и вычитание
Сложение и вычитание двух комплексных
чисел выполняются аналогично сложению и
вычитанию соответствующих им радиусвекторов на комплексной плоскости, т.е. если
даны два комплексных числа