Комплексные числа

1.

Комплексные числа
ПТПИТ им. Б.Г. Изгагина
Разработка преподавателя
математики
Гуляевой Е.Ю.

2. Множество каких чисел представлено на оси ?

3.

Компания действительных чисел очень пёстрая – здесь и целые числа, и
дроби, и иррациональные числа. При этом каждой точке числовой прямой
обязательно соответствует некоторое действительное число.

4.

Понятие комплексного числа
Х+А=В - недостаточно положительных
Х+5=2чисел
А·Х + В=0 (А≠0) – разрешимы на
множестве рациональных чисел
Х²=2 или Х³=5 - корни - иррациональные
числа
Решение квадратных уравнений

5. Решение квадратных уравнений

А · Х² + В ·Х + С = 0
При D < 0 действительных корней нет
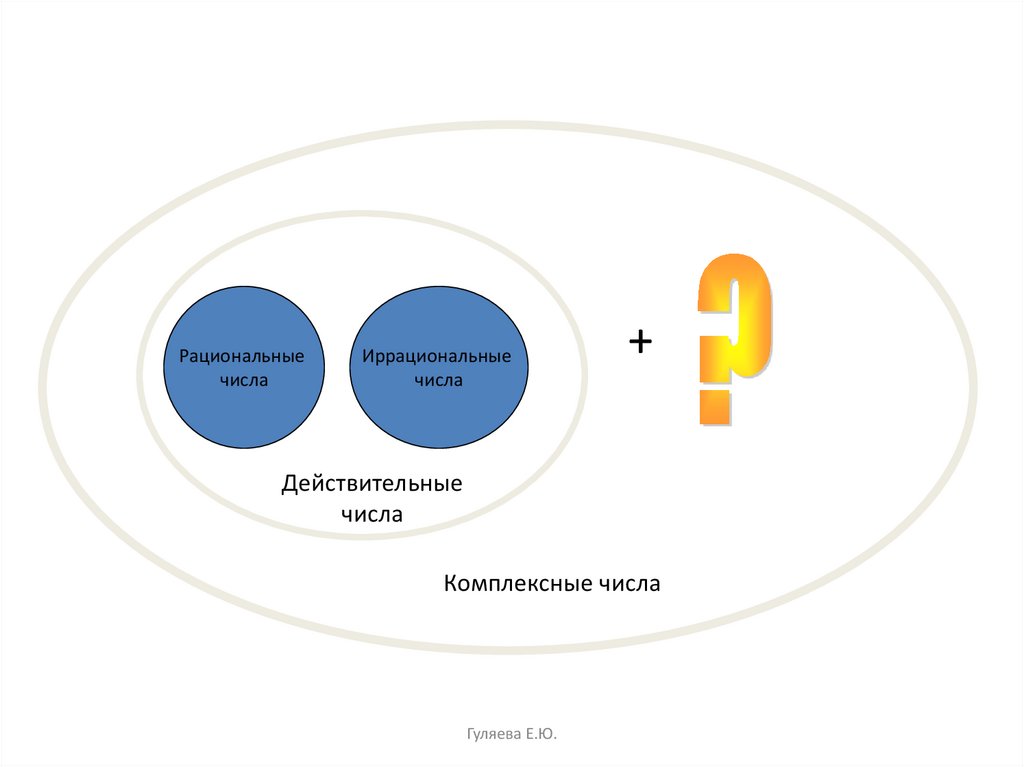
Рациональные
числа
Иррациональные
числа
Действительные
числа
+

6.

Рациональные
числа
Иррациональные
числа
+
Действительные
числа
Комплексные числа
Гуляева Е.Ю.

7.

Не пытайтесь представить комплексное
число «в жизни» – это всё равно, что
пытаться представить четвертое
измерение в нашем трехмерном
пространстве.

8.

9.

10. Комплексное число имеет вид:

а и b– действительные числа,
i – так называемая мнимая
единица.
Алгебраическая форма комплексного числа.

11. z = a + bi

Действительная часть (ReZ)
Мнимая часть (ImZ)

12. Геометрическая интерпретация комплексного числа

Мнимая ось
Действительная ось
Комплексная плоскость С
Гуляева Е.Ю.

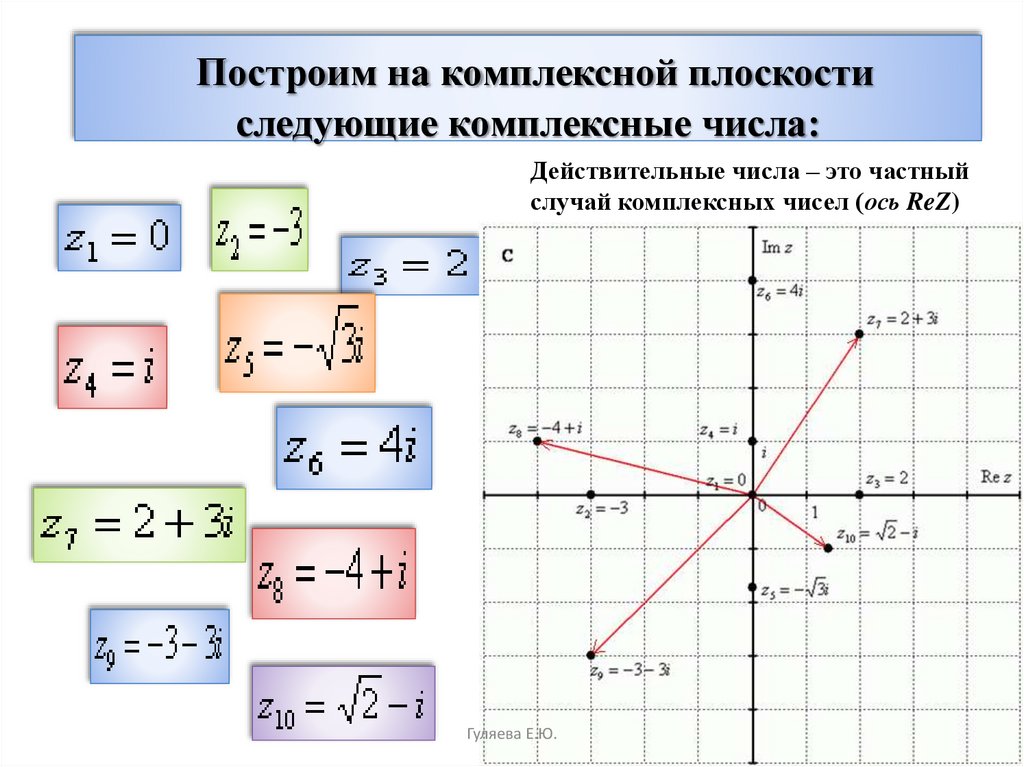
13. Построим на комплексной плоскости следующие комплексные числа:

Действительные числа – это частный
случай комплексных чисел (ось ReZ)
Гуляева Е.Ю.

14.

Действия с комплексными числами

15. Сложение комплексных чисел

Геометрическая форма
Алгебраическая форма
Сумма
(A+Вi) + (C+Di)=
(A+C)+(B+D)i
Пример. Сложить два комплексных
числа:
Гуляева Е.Ю.

16. Геометрическое изображение разности комплексных чисел

Вычитание – операция,
обратная сложению:
Z+ Z2 = Z1
Z= Z1 - Z2 –разность
Пример. Найти разность
комплексных чисел , если:
Гуляева Е.Ю.

17. Умножение комплексных чисел

Пример. Найти произведение комплексных чисел:
Раскроем скобки по правилу умножения многочленов:
Гуляева Е.Ю.

18. Деление комплексных чисел

Пример. Найти частное комплексных чисел:
Деление чисел осуществляется методом умножения
знаменателя и числителя на сопряженное знаменателю
выражение.

19. Домашнее задание

• Изучить
презентацию и
составить конспект
• Найти сумму,
разность,
произведение и
частное двух
комплексных чисел:
Гуляева Е.Ю.