Похожие презентации:
Дедуктивные теории. Глава 5
1.
Глава 5ДЕДУКТИВНЫЕ ТЕОРИИ
1
2.
ДЕДУКЦИЯ, ИНДУКЦИЯДедукция ( deductic – выведение ) - форма мышления, когда
заключение выводится логическим путем из некоторых посылок.
Индукция ( inductio – наведение ) - форма мышления, когда от
некоторых фактов или истинных высказываний переходят к гипотезе
(общему утверждению).
Дедуктивные рассуждения.
1. Все люди смертны. Сократ – человек. Следовательно, Сократ
смертен.
2. 5 > 3, 3 > 1, следовательно, 5 > 1.
Примеры индуктивных рассуждений.
у 2 х 1 прямая
1. График функции
, следовательно, графиком
у х 2 прямая
для y = k x + b является прямая.
n
2. Пусть р = 2 2 + 1. При n = 0, 1, 2, 3, 4 получим, что р равно 3, 5, 17,
257, 65537 и все они простые числа, предполагаем, что все числа р
простые (гипотеза Ферма). Эйлер показал, что для
n=5
р = 4 294 967 297
и делится на 641. Следовательно, предположение Ферма не верно.
2
3.
ЗАДАНИЕ ДЕДУКТИВНОЙ ТЕОРИИДедуктивная теория заданна если:
1) задан алфавит;
2) заданы правила образования формул; Ф - множество формул;
из Ф выделено дедуктивным способом подмножество Т, элементы
которого называются теоремами.
Т можно задать:
I. а) Из Ф выделяется подмножество А, элементы которого называются
аксиомами – заданы аксиомы;
б) задается конечное число правил выводов.
Эта теория называется формальной аксиоматической теорией (ФАТ).
Аксиомы не доказываются не потому, что могут не доказываться,
а потому, что не могут быть доказаны.
II.
III.
а) Заданы аксиомы;
б) правила вывода считаются известными.
Это полуформальная аксиоматическая теория (ПАТ).
а) Аксиом нет;
б) задается конечное число правил выводов.
Такую теорию называют теорией естественного вывода (ТЕВ).
3
4.
СВОЙСТВА ДЕДУКТИВНЫХ ТЕОРИЙФ
Т
Дедуктивные теории, в которых множество теорем Т = Ф, называются
противоречивыми, в противном случае – непротиворечивыми.
Свойство
полноты
дедуктивной
теории
характеризует
достаточность теорем для каких-то целей. В зависимости от целей
вводятся различные понятия полноты.
Независимость аксиом. Аксиома А k называется независимой, если
А k нельзя доказать из остальных аксиом. Система аксиом называется
независимой, если каждая из них независима от остальных.
Разрешимость теории. Дедуктивная теория наз-ся разрешимой,
если существует метод, позволяющий для произвольной формулы А за
конечное число действий выяснить, является А теоремой или нет.
4
5.
ПОЛУФОРМАЛЬНАЯАКСИОМАТИЧЕСКАЯ ТЕОРИЯ
5
6.
ПОЛУФОРМАЛЬНАЯ АКСИОМАТИЧЕСКАЯ ТЕОРИЯ - ГЕОМЕТРИЯГеометрия Евклида (330 – 275 гг. до н.э.) «Начала».
Аксиоматика Гильберта:
1. Задано три различных множества:
а) элементы 1-го множества называются
точками и обозначаются через А,В,С,...;
б) элементы 2-го называются прямыми и
обозначаются через а, b,с,...;
в) элементы 3-го множества
обозначаются через , , ,....
называются
плоскостями
и
На множестве точек, прямых и плоскостей введены отношения,
обозначаемые словом «лежат», «между» и «конгруэнтно».
6
7.
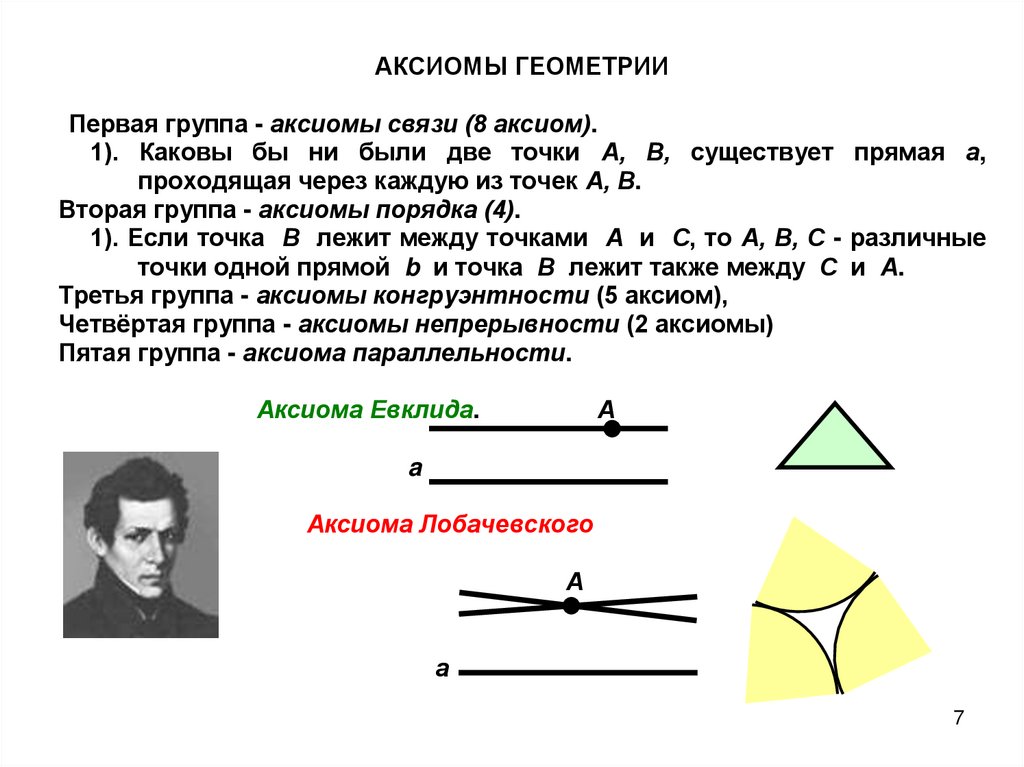
АКСИОМЫ ГЕОМЕТРИИПервая группа - аксиомы связи (8 аксиом).
1). Каковы бы ни были две точки А, В, существует прямая а,
проходящая через каждую из точек А, В.
Вторая группа - аксиомы порядка (4).
1). Если точка В лежит между точками А и С, то А, В, С - различные
точки одной прямой b и точка В лежит также между С и А.
Третья группа - аксиомы конгруэнтности (5 аксиом),
Четвёртая группа - аксиомы непрерывности (2 аксиомы)
Пятая группа - аксиома параллельности.
Аксиома Евклида.
А
a
Аксиома Лобачевского
А
а
7
8.
ФОРМАЛЬНАЯАКСИОМАТИЧЕСКАЯ
ТЕОРИЯ
(ИСЧИСЛЕНИЕ
ГИЛЬБЕРТОВСКОГО ТИПА)
8
9.
ФОРМАЛЬНАЯ АКСИОМАТИЧЕСКАЯ ТЕОРИЯ (ФАТ)ФАТ задана если заданы:
1. Алфавит теории.
2. Формулы.
3. Аксиомы.
4. Конечное число правил вывода R1, R2,..., Rn, согласно каждому из
которых
некоторая
формула,
именуемая
непосредственным
следствием, непосредственно выводима из некоторого конечного
множества формул, называемых посылками.
Вывод в ФАТ - последовательность A 1 , A 2 ,...,A n формул, такая, что
A i аксиома
для каждого i (1 i n): A i
A i непоср. следствие
Формула А теории B наз-ся теоремой теории B, если вывод в B, в
котором последней формулой является A.
Формула А - следствие множества формул G тогда и только тогда,
когда существует такая последовательность формул A 1 , A 2 ,..., A n , что
A i аксиома
A n = A и A i A i непоср. следствие
Тогда пишем: G├A
A формула из G
i
Элементы G – гипотезы.
├А
«формула А является теоремой».
9
10.
СВОЙСТВА ВЫВОДИМОСТИ1. Если G F и если G ├ A , то F ├ A.
2. G ├ A когда в G конечное подмножество Н такое, что Н ├ А.
3. Пусть G ├ A и формула В из G, выводима из F, тогда F ├ A.
3* . Если A ├ B и B ├ C, то А ├ C.
4. Если G , A ├ B и G ├ A , то G ├ B.
10
11.
ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ ( ТЕОРИЯ L )1. Символы L : , , ) , (, А 1 , А 2 , А 3 , ...
2. Формулы L :
1) все буквы А 1 , А 2 , А 3,... суть формулы;
2) если А и В формулы, то ( А ) и ( А В ) тоже формулы;
3) выражение теории L является формулой только тогда, когда
это следует из 1) и 2).
Будем считать, что: А & В ( ( А ( В ))), А В (( А ) В ),…
3. Аксиомы L. Для формул А, В и С теории L, следующие формулы
суть аксиомы L:
А1: А ( B А );
A2: ( А ( B C )) (( А B ) ( А C ));
A3: ( B А ) (( B А ) B ).
4. Правило вывода теории L : modus ponens (МР):
В есть непосредственное следствие А и А В.
МР означает: А , А В В .
11
12.
НЕКОТОРЫЕ ТЕОРЕМЫ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙЛемма 1. Для формулы А теории L формула А А является
теоремой этой теории L .
Теорема (теорема дедукции). Если Г - множество формул, А, В формулы и Г , А ├ В, то Г ├ А В. В частности, если А ├ В, то ├ А В.
Следствие 1. A B, B C ├ A C.
Следствие 2. A ( B C ), B ├ A C.
Лемма 2. Для формул А, В следующие формулы являются
теоремами в L:
а) B B;
б) B B;
в) A ( A B );
г) ( В A ) ( A B );
д) ( A B ) ( B A );
е) A ( B ( A B ));
ж) ( A B ) (( A B ) B ).
12
13.
ДВА ОПРЕДЕЛЕНИЯ НЕПРОТИВОРЕЧИВОСТИПервое определение. Дедуктивная теория наз-ся противоречивой,
если Т = Ф и непротиворечивой если Т Ф .
Второе определение. Дедуктивная теория наз-ся противоречивой,
если формула А такая, что ├ A и ├ A ; если такой формулы не , то
теория наз-ся непротиворечивой.
Теорема 5.2. Для теорий, содержащих исчисление высказываний,
приведенные определения (не) противоречивости эквивалентны.
13
14.
ДОКАЗУЕМЫЕ ПРАВИЛА ВЫВОДА В LПравило modus ponens:
A, A B
B
теорема дедукции:
G, A ├ B; G
A B
;
Правила:
перевертывания: G, A ├ B; G, B ;
A
удаления &:
A& B
A& B
A, B
&,
& ; введения &:
&,
A
B
A& B
введения :
A
A
,
; сведения к нелепости: А├ В, А├ В .
A B
B A
А
A, B
&;
B& A
доказательства разбором случаев: А ├ С, В ├ С, А В ;
С
14
15.
СВОЙСТВА ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙНепротиворечивость
Теорема. Исчисление высказываний непротиворечиво, т.е. не
формулы А такой, чтобы А и А были ее теоремами.
Теория L полна в широком смысле, если в ней доказуема каждая
формула, являющаяся тавтологией.
Ф
╞А ├А
Теория L полна в узком смысле, если присоединение к ее аксиомам
какой-нибудь, не выводимой в ней формулы, приводит к
противоречивой теории.
В
А1, А2, А3 Т
Теорема (о полноте). Если формула А теории L является
тавтологией, то она является теоремой теории L.
15
16.
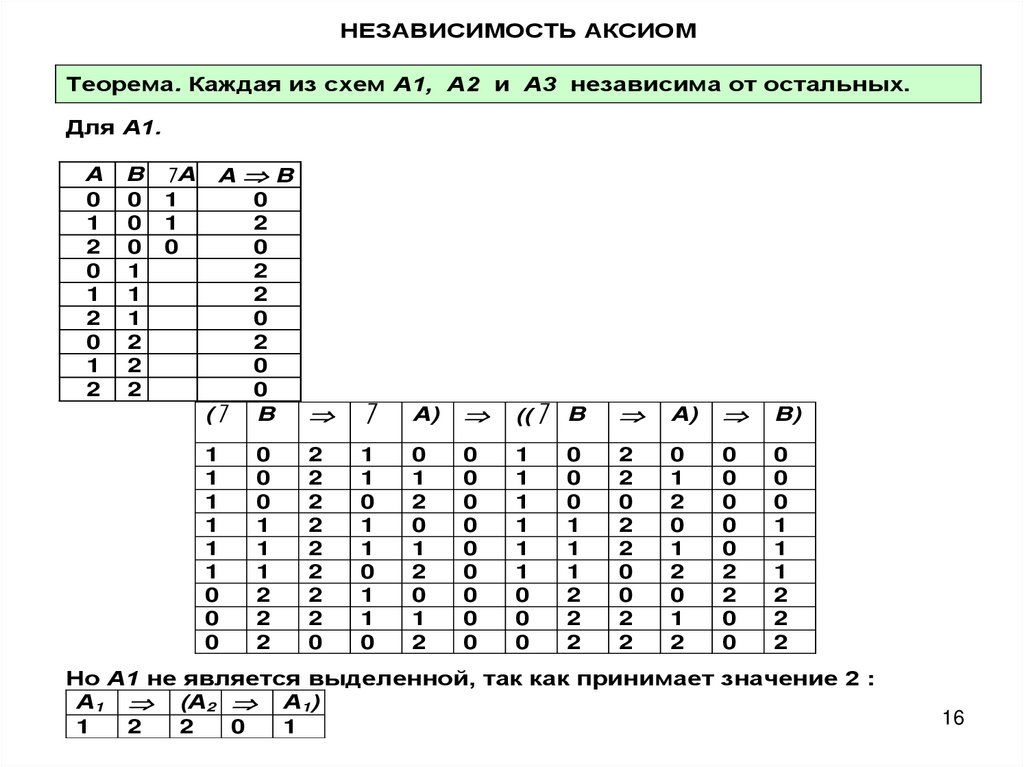
НЕЗАВИСИМОСТЬ АКСИОМТеорема. Каждая из схем А1, А2 и А3 независима от остальных.
Для А1.
A
0
1
2
0
1
2
0
1
2
B
0
0
0
1
1
1
2
2
2
A
1
1
0
A B
0
2
0
2
2
0
2
0
0
(
B
A)
((
B
A)
B)
1
1
1
1
1
1
0
0
0
1
1
0
1
1
0
1
1
0
0
1
2
0
1
2
0
1
2
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
0
0
0
0
0
0
1
1
1
2
2
2
2
2
0
2
2
0
0
2
2
0
1
2
0
1
2
0
1
2
0
0
0
0
0
2
2
0
0
0
0
0
1
1
1
2
2
2
0
0
0
1
1
1
2
2
2
2
2
2
2
2
2
2
2
0
Но А1 не является выделенной, так как принимает значение 2 :
А1 (А2 А1)
1
2
2
0
1
16
17.
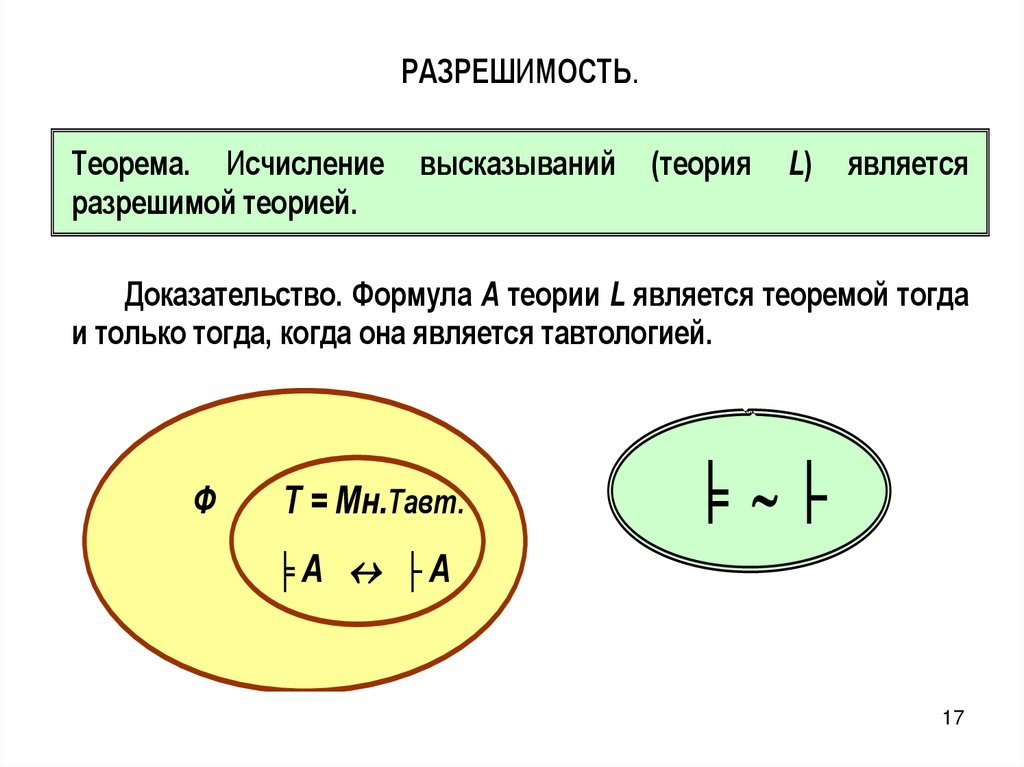
РАЗРЕШИМОСТЬ.Теорема. Исчисление
разрешимой теорией.
высказываний
(теория
L)
является
Доказательство. Формула А теории L является теоремой тогда
и только тогда, когда она является тавтологией.
Ф
Т = Мн.Тавт.
╞ ├
╞А ├А
17
18.
ТЕОРИИ ПЕРВОГО ПОРЯДКА1. Символы: , - пропозициональные связки;
,
( , ) , - знаки пунктуации;
х 1 , х 2 ,... - счетное множество предметных переменных;
а 1 , a 2 ,... - конечное (возможно и пустое) или счетное множество
предметных констант;
A ik ( i , k 0) - непустое, конечное или счетное мн-во предикатных
букв;
f ik ( i, k 1 ) - конечное (возможно и пустое) или счетное мн-во
функциональных букв;
x i , x i ( i 1 ) - кванторы.
Сигнатура – набор из трех множеств = Сnst, Fn, Pr , где
Сnst - множество постоянных (констант);
Fn - множество функциональных букв;
Pr - множество предикатных букв.
2. Формулы теории первого порядка - формулы логики предикатов.
18
19.
ТЕОРИИ ПЕРВОГО ПОРЯДКА ( ТЕОРИИ К )3. Аксиомы теории К:
Логические аксиомы: для формул А, В, C имеем аксиомы:
А1: A ( B A );
A2: ( A ( B C )) (( A B ) ( A C ));
A3: ( B A ) (( B A ) B );
A4: xi A ( x I ) A ( t ),
здесь t терм теории К, свободный для xi в А ( x i );
A5: xi ( A B ) ( A xi B ), если А не содержит свободных
вхождений xi.
Собственные аксиомы у каждой теории свои.
4. Правила вывода:
1) modus ponens: А , А B ├ В;
2) правило обобщения ( Gen ): А ├ xi А.
19
20.
АРИФМЕТИКАСистема аксиом ( Дедекинд, Пеано ):
Р 1 : 0 - есть натуральное число;
Р 2 : для натурального числа х другое натуральное число,
обозначаемое х’ и называемое непосредственно следующим за х;
Р 3 : 0 х’ для натурального числа х;
Р 4 : если х’ = у’, то х = у;
Р 5 : если U есть свойство, которым, быть может, обладают одни и
не обладают другие натуральные числа, и если:
1) натуральное число 0 обладает свойством U и
2) для натурального числа х из того, что х обладает свойством U
следует, что и натуральное число х’ обладает свойством U,
то свойством U обладают
математической индукции).
все
натуральные
числа
(принцип
20
21.
ФОРМАЛЬНАЯ АРИФМЕТИКА ( ТЕОРИЯ S )S - теория 1 - го порядка, имеющая символы: A 12 , a 1 , f 11, f 12 , f 22 ,
,
, , ) , ( , , x 1 , x 2 ,..., x 1 , x 2 ,..., x 1 ,…, x 2 ,…
A 12 ( t , s ) через t = s,
a1
f 11 ( t )
f 12 ( t , s ) через t + s,
через t’,
через 0,
f 22 ( t , s ) через t s ( - знак умножения).
Собственные аксиомы формальной арифметики:
S1: x1 = x2 (( x1 = x3 ) ( x2 = x3 ));
S2: x1 = x2 x1‘ = x2‘ ;
S3: 0 x1‘;
S4: x1‘ = x2‘ x1 = x2;
S5: x1 + 0 = x1;
S6: x1 + x2‘ = ( x1 + x2 )’;
S7: x1 0 = 0;
S8: x1 x2‘ = x1 x2 + x1;
S9: A ( 0 ) ( xi ( A ( x I ) A ( x I ’ )) xi A ( xi )),
где А(xi) - произвольная формула теории S.
Правила вывода: МР и Gen.
21
22.
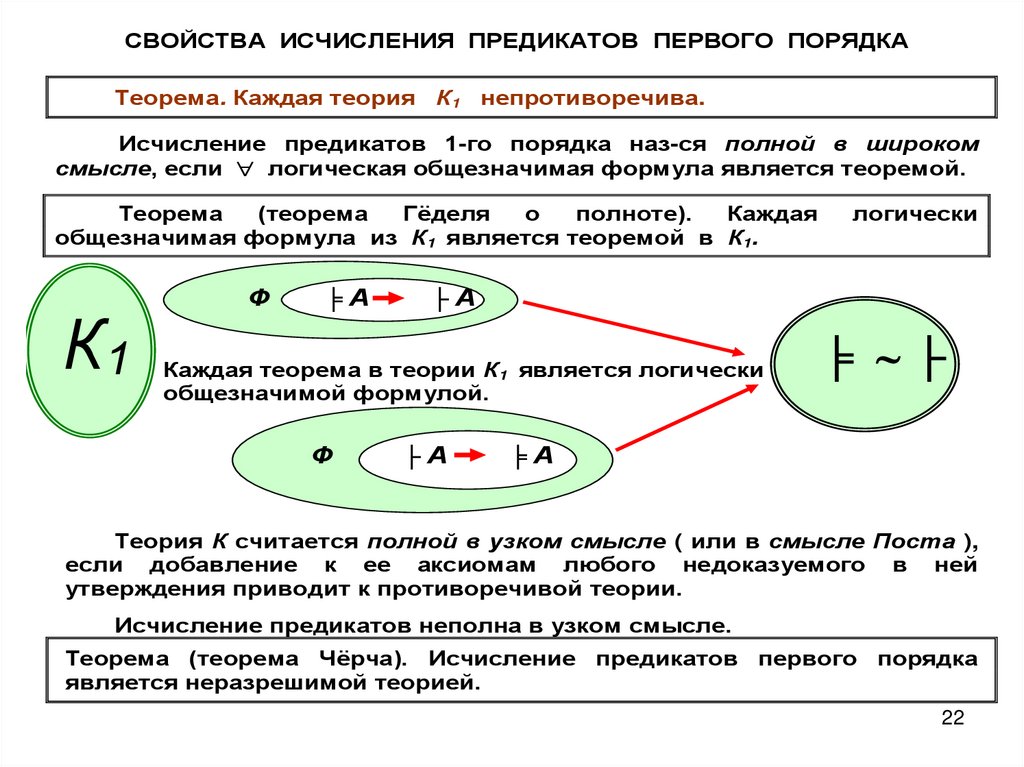
СВОЙСТВА ИСЧИСЛЕНИЯ ПРЕДИКАТОВ ПЕРВОГО ПОРЯДКАТеорема. Каждая теория
К1
непротиворечива.
Исчисление предикатов 1-го порядка наз-ся полной в широком
смысле, если логическая общезначимая формула является теоремой.
Теорема
(теорема
Гёделя
о
полноте).
Каждая
общезначимая формула из К1 является теоремой в К1.
К1
Ф
╞А
├А
Каждая теорема в теории К1 является логически
общезначимой формулой.
Ф
логически
├А
╞ ├
╞А
Теория К считается полной в узком смысле ( или в смысле Поста ),
если добавление к ее аксиомам любого недоказуемого в ней
утверждения приводит к противоречивой теории.
Исчисление предикатов неполна в узком смысле.
Теорема (теорема Чёрча). Исчисление предикатов первого порядка
является неразрешимой теорией.
22
23.
СВОЙСТВА ТЕОРИЙ ПЕРВОГО ПОРЯДКАПервая теорема Геделя утверждает, что каждая ФАТ К , содержащая
формальную арифметику такова, что если К непротиворечива, то К
существенно неполна.
Вторая теорема Геделя. Если теория К , содержащая арифметику,
непротиворечива, то непротиворечивость ее нельзя доказать
средствами самой теории К.
Аксиоматический метод позволяет:
1) систематизировать научный материал;
2) обеспечить определенную организацию научного знания;
3)
исследовать
структуру
различных
теорий
и
взаимоотношение;
4) обеспечить необходимую строгость рассуждений.
их
Д. Гильберт: "Под знаком аксиоматического метода математика
проявляет свою руководящую роль в науке вообще".
23
24.
ПОИСК КОНТРПРИМЕРАПусть дана формула W логики высказываний, которая возможно
не является тавтологией, следовательно, может быть существуют
означивание переменных, при которых она ложна. Как это выяснить?
Естественно посмотреть на структуру формулы W.
Если W имеет вид:
А B,
то надо найти значения переменных, при которых А = И, а B = Л.
Если W имеет вид:
А B,
то надо найти значения переменных, при которых А = B = Л.
Если W имеет вид:
А&B, то … .
Тем самым задача поиска контрпримера для формулы
W
сводится к
одной или нескольким аналогичным задачам.
24
25.
СЕКВЕНЦИЯСеквенцией называется выражение вида Г , где Г и — некоторые
конечные множества формул, знак разделяет эти множества формул.
С каждой секвенцией
Г
связывают задачу поиска таких
значений переменных, при которых все формулы из Г истинны, а все
формулы из ложны. Такой набор значений называется контрпримером
Г .
к секвенции
Пусть Г = {A1 , A2 ,…An }, = {B1 , B2 ,…, Bm }. Тогда контрпримеры к
секвенции Г — это контрпримеры к формуле
W = A1 & A2 &…& An B1 B2 … Bm.
то есть те наборы значений, при которых формула W ложна. При этом
конъюнкцию
пустого
истинной,
дизъюнкцию
а
множества
пустого
формул
считаем
множества
тождественно
формул
считаем
тождественно ложной.
25
26.
СВЕДЕНИЕ ЗАДАЧИ ПОИСКА КОНТРПРИМЕРА К ФОРМУЛЕ КЗАДАЧЕ ПОИСКА КОНТРПРИМЕРА К СЕКВЕНЦИИ
Задача поиска контрпримера к формуле В может быть сформулирована как
задача поиска контрпримера к секвенции:
{В}.
а вместо {А}
{В}
Вместо
будем записывать
будем записывать:
В,
А
Пусть в левой и правой частях секвенции встречаются одинаковые
формулы, например, D содержится и слева и справа секвенции. Тогда в
формуле W будет содержаться D D поэтому W является тавтологией
и не может быть ложной, и, следовательно, W не имеет контрпримера.
Пример. Секвенция
А А,В
не имеет контрпримера, так как
формула W = А А В А А В тавтология, а секвенция А В, С
имеет контрпример, так как формула W = А В С
А В С будет
ложна, когда А = И, В = С = Л.
26
27.
ЗАДАНИЕ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ В ВИДЕИСЧИСЛЕНИЯ СЕКВЕНЦИЙ
Исчисление секвенций для высказываний обозначают как систему G’.
1. Символами G’ являются: , &, , , ),( и буквы А1, А2, А3,...
2. Формулы G’ задаются так же, как в логике высказываний.
3. Аксиомы. В G’ аксиомами являются секвенции, в левой и правой
частях которых формулами являются только атомарные формулы, причем
некоторая формула встречается в обеих частях секвенции.
Пример аксиомы: А, В А.
Очевидно, что аксиома не имеет контрпримера.
27
28.
ЗАДАНИЕ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ В ВИДЕИСЧИСЛЕНИЯ СЕКВЕНЦИЙ - ПРАВИЛА
4. Правила вывода задаются в форме:
секвенция
секвенция
или
секвенция
секвенция
секвенция
Верхние секвенции считаются посылками, а нижние - заключениями.
Справа от правил могут записываться связки , &, , , которые
исключаются по этим правилам.
В каждом правиле считается, что нижняя секвенция имеет контрпример
тогда и только тогда, когда хотя бы одна из верхних секвенций имеет
контрпример.
28
29.
ИСЧИСЛЕНИЯ СЕКВЕНЦИЙ - ПРАВИЛАПусть Г и — некоторые конечные множества формул из G’, а А и В
произвольные формулы из G’. Правилами выводов в системе G’
считаются следующие:
а)
Г В,
Г А,
Г А & В,
б)
А, В , Г
А & В, Г
в)
Г А, В ,
Г А В,
г)
В, Г
А, Г
А В, Г
д)
Г , А В,
Г А В,
е)
Г, В
Г А,
А В, Г
ж)
А, Г
Г А ,
з)
Г А,
А, Г
Г, А обозначает Г {A}. Каждое правило применяется для анализа одной из
формул нижней секвенции.
29
30.
ИСЧИСЛЕНИЕ СЕКВЕНЦИЙ – ИСПОЛЬЗОВАНИЕ ПРАВИЛКак пользоваться правилами? Возьмём секвенцию, к которой мы
ищем контрпример. Выбираем в ней последовательно (лексографически)
формулу сначала слева затем справа секвенции, посмотрим на главную
связку и применим соответствующее правило, написав одну или две
секвенции над исходной. Затем к каждой из них снова применим одно из
правил и т. д. Постепенно будет расти «дерево поиска контрпримера»,
причём исходная секвенция будет иметь контрпример тогда и только тогда,
когда одна из верхних секвенций (стоящих в «листьях») этого дерева имеет
контрпример.
Этот процесс обрывается в том случае, если все формулы в
оставшихся секвенциях представляют собой атомы (переменные), тогда ни
одно из наших правил поиска контрпримера не применимо. К этому
моменту всё становится ясным: если в левой и правой части секвенции
есть общий атом (формула, переменная), то к ней нет контрпримера. Если
же левая и правая части секвенции не пересекаются, то контрпример есть.
30
31.
Пример.Для формулы А формула
А А доказуема
в теории
L.
Будет ли
А А - доказуемой в G’ ?
Иначе, имеет ли секвенция
(А А)
По правилу д) получим :
контрпример ?
А А ( Г = , = ),
а эта секвенция является аксиомой и контрпримера не
имеет, следовательно,
А А - доказуема в G’ .
31
32.
Лемма 1 (в теории L). Для формулы А формула А А – теорема в LДоказательство:
1) (А ((А А) А)) ((А (А А)) (А А)) аксиома по А2,
если В=А А и С=А;
2) А ((А А) А)
аксиома по схеме А1, если В=А А;
3) (А (А А)) (А А)
непоср. следствие из 1) и 2) по МР;
4) А (А А)
аксиома по схеме А1 при В=А;
5) А А
непоср. следствие из 3) и 4) по МР.
32
33.
ИСЧИСЛЕНИЕ СЕКВЕНЦИЙ – ПРИМЕР 1Пример 1. Пусть имеем секвенцию:
А (В А)
Используя правило д) получим (здесь Г= { }, ={ }):
А (В А)
Теперь, вновь используем это правил д), но с Г = {А}.
А, В А
В результате получим:
Полученная секвенция является аксиомой и не имеет контрпримера,
следовательно, исходная секвенция выводима. Отметим, что формула
А (В А)
является
тавтологией
и
выводима
в
формальной
аксиоматической системе - теории L. Описанный вывод секвенции
представляют в виде следующего дерева вывода:
A, B A
A (B A)
A (B A)
33
34.
ИСЧИСЛЕНИЕ СЕКВЕНЦИЙ – ПРИМЕР 2(С D) D
Пример 2. Пусть имеем секвенцию:
Используя правило д) получим (здесь Г= { }, ={ }):
С D D
Теперь используя правил е), но с = {D}, получим две секвенции:
С, D
и
D D
Вторая секвенция является аксиомой и не имеет контрпримера, но первая
имеет контрпример: С= D=Л. Тогда исходная секвенция не выводима. Эти
выкладки представляются следующим деревом вывода:
C ,D
D D
C D D
(C D ) D )
Легко видеть, что формула (С D) D не является тавтологией и не
выводима и в формальной аксиоматической системе - теории L.
34
35.
ИСЧИСЛЕНИЕ СЕКВЕНЦИЙ – ПРИМЕР 3Пример 3. Пусть имеем секвенцию
((А В) А) А
Поиск контрпримера (вывода) можно развернуть и в последовательность
секвенций, но запишем в обычном для исчисления секвенции виде,
именно, в виде дерева, как в рассмотренных примерах 1 и 2:
A A, B
A A
A, A B
( A В) А A
(( A В ) А ) A
Здесь обе секвенции А А,В и А А, находящиеся в листьях дерева,
являются аксиомами и не имеют контрпримеров. Следовательно, формула
((А В) А) А является тавтологией и исходная не имеет контрпримера, а
имеет вывод в G’.
35
36.
АЛГОРИТМ ПОИСКА КОНТРПРИМЕРАПоиск контрпримера представим в виде алгоритма, использующего
процедуры поиск (search) и раскрытия формулы (expand).
В процедуре поиск (search) алгоритм просматривает все листья
строящегося дерева вывода слева направо. Для каждого листа, не
являющегося атомарной формулой, вызывается процедура раскрытия
формулы (expand).
Процедура expand строит поддерево, выбирая подходящее правило
вывода, чтобы исключить из неатомарной формулы главную связку.
Алгоритм продолжает работу до тех пор, пока каждый лист станет
атомарной формулой. После того как все листья составлены из секвенций
только с атомарными формулами делается заключение: если все листья
аксиомы, то контрпримера нет и исходная секвенция выводима, иначе
контрпример существует и секвенция не выводима.
36
37.
PROCEDURE SEARCHprocedure search(Г : sequent; var T : tree};
begin
let T be the one-node tree labeled with Г ;
while not all leaves of T are finished do
T0 := T;
for each leaf node of T0
(in lexicographic order of tree addresses) do
if not finished(node.) then
expand(node, T)
endif
endfor
endwhile;
if all leaves are axioms
then
write ('T is a proof of Г ’)
else
write (Г is falsifiable')
endif
end.
37
38.
PROCEDURE EXPANDprocedure expand(node : tree-address; var T : tree);
begin
let A1,...,An B1,...,Bm be the label of node;
let S be the one-node tree labeled with
A1,...,An B1,...,Bm
for i :— 1 to m do
if nonatomic(Ai) then
S := the. new tree obtained from S by
applying to the descendant of Ai
in every nonaxiom leaf of S
the left rule applicable to Ai
endif
endfor;
for i \— I to n do
if nonatomic(Bi) then
S := the new tree obtained from S
by applying to the descendant of Bi
in every nonaxiom leaf of S
the right rule applicable to Bi
endif
endfor;
T := dosubstitution(T,node1 S}
end.
38
39.
ОСНОВНАЯ ТЕОРЕМА ИСЧИСЛЕНИЯ СЕКВЕНЦИЙ ДЛЯ ЛВТеорема 4.11 (корректность и полнота исчисления секвенций).
Секвенция выводима тогда и только тогда, когда она не имеет
контрпримера.
Чем уж так интересно исчисление секвенций? Какая, собственно
говоря, разница — иметь дело с секвенциями или с выводом в
гильбертовском исчислении?
39
40.
ОСНОВНОЕ ПРЕИМУЩЕСТВО ИСЧИСЛЕНИЯ СЕКВЕНЦИЙПринципиальное
различие
Исч.-Гильберта
и
Исч.-Генцена
в
следующем.
Правила вывода в исчислении секвенций таковы, что в их
верхнюю часть входят только подформулы формул, встречающихся в
нижней части. Поэтому в выводе какой-то секвенции не может
встретиться ничего нового, чего не было в самой секвенции.
В гильбертовском исчислении это не так: мы можем вывести
формулу В из формул А В и А, при этом А может быть совершенно
произвольной. Поэтому поиск вывода снизу вверх
для исчисления
секвенций происходит сравнительно однозначно (мы можем поразному выбирать расчленяемую формулу, но и только), в то время
как в гильбертовском исчислении, начав с интересующей нас формулы
В трудно указать, из чего бы мы могли получить ее вывод.
40
41.
ТЕОРИИ ЕСТЕСТВЕННОГОВЫВОДА - ТЕВ
(НАТУРАЛЬНАЯ ДЕДУКЦИЯ)
41
42.
ТЕОРИЯ ЕСТЕСТВЕННОГО ВЫВОДАЗаданы: 1) алфавит;
выводов.
2) формулы;
3) аксиом нет;
4) правила
Исчисление высказываний в виде теории естественного вывода.
1. Символы: , &, , , (, ), A1, A2,...,
2. Формулы: пропоз. формы, образ-ые из A1, A2,... с помощью , &, , .
3. Правила вывода:
Правила введения:
A, B
&;
A& B
A, B
&;
B& A
A
A
;
; A├ B ;
A B
B A
A B
A├ B, B .
A
Правила исключения ( удаления ):
A& B
A& B
&;
& ; A├ C, B ├ C, A B ;
A
B
С
A
А
;
A, A B
.
B
42
43.
ТЕОРИЯ ЕСТЕСТВЕННОГО ВЫВОДАЗаданы: 1) алфавит;
выводов.
2) формулы;
3) аксиом нет;
4) правила
Исчисление высказываний в виде теории естественного вывода.
1. Символы: , &, , , (, ), A1, A2,...,
2. Формулы: пропоз. формы, образ-ые из A1, A2,... с помощью , &, , .
3. Правила вывода:
Правила введения:
A, B
&;
A& B
A, B
&;
B& A
A
A
;
; A├ B ;
A B
B A
A B
A├ B, B .
A
Правила исключения ( удаления ):
A& B
A& B
&;
& ; A├ C, B ├ C, A B ;
A
B
С
A ;
А
A, A B
.
B
43
44.
ДОКАЗАТЕЛЬСТВОВ
ТЕВ
├ (A B&C ) (A B)&(A C)
введение
(A B&C )├ (A B) & (A C)
удаление
удаление
A ├ (A B)&(A C)
B&C ├ (A B)&(A C)
введение &
введение &
A ├ A B
A ├ A C
введение
введение
B&C ├ A B
B&C ├ A C
введение
введение
B&C ├ B
B&C ├ C
удаление &
удаление &
44
45.
СРАВНЕНИЕ Т Е В С ИСЧИСЛЕНИЕМ СЕКВЕНЦИЙНатуральная дедукция (теория естественного вывода) похожа на
исчисление секвенций, но есть существенное различие.
В натуральной дедукции есть правила введения и исключения, а в
исчислении секвенций только правила исключения.
Поэтому натуральная дедукция менее удобна для автоматизации
доказательств, ибо здесь рассуждения, хотя и естественны для
рассуждений, но менее унифицированы.
45









































 Математика
Математика Философия
Философия








