Основные понятия и определения сопротивления материалов. Лекция 2.1.1

1.

ПРИКЛАДНАЯ МЕХАНИКА
Раздел 2. СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
ЛЕКЦИЯ 2.1.1
Основные понятия и
определения сопротивления
материалов
© САНКТ-ПЕТЕРБУРГСКИЙ УНИВЕРСИТЕТ ГПС МЧС РОССИИ, IGPS.RU, 2020.

2.

Кафедра Механики и Инженерной графики
Вопросы лекции:
1. Основные понятия сопротивления материалов.
2. Метод сечений.
3. Центральное растяжение-сжатие.
4. Определение внутренних усилий.

3.

Кафедра Механики и Инженерной графики
Вопрос 1. Основные понятия сопротивления материалов
Прикладная наука об инженерных методах расчёта на прочность,
жесткость и устойчивость деталей машин и конструкций, называется
сопротивлением материалов.
Способность конструкции воспринимать заданную нагрузку, не разрушаясь и
без остаточных деформаций, называют прочностью.
Способность сооружений и ее частей под нагрузкой сохранять свои
размеры
и
форму
в
установленных
нормами
пределах
называется жесткостью.
Способность конструкции, и ее частей, сохранять под нагрузкой
первоначальную форму упругого равновесия называется устойчивостью.
Основной задачей сопротивления материалов является разработка
методов расчета на прочность, жесткость и устойчивость с целью получения
надежных и экономически обоснованных размеров элементов конструкций

4.

Кафедра Механики и Инженерной графики
Реальный объект и расчетная схема
Реальный объект, освобожденный от несущественных
особенностей, не влияющих заметным образом на работу системы в
целом, называется расчетной схемой. Расчетная схема выбирается
так, чтобы существенно упростить расчет, не искажая
действительной картины работы конструкции или детали.
Расчетную схему составляют в следующем
порядке:
1. Разбивают конструкцию на простые
элементы
2. Каждый простой элемент конструкции
заменяют соответствующим расчетным
элементом (брусом, пластиной, оболочкой,
массивным телом);
3. Выбирают схему опорных частей элемента
или конструкции (подвижный и неподвижный
шарнир, жесткая заделка и другие);
4. Выбирают вариант соединения элементов
конструкции между собой и с опорными
частями (жесткий или шарнирный) .

5.

Кафедра Механики и Инженерной графики
Расчетные формы и их классификация
Брусом называется расчетный элемент, длина которого значительно больше размеров
его поперечного сечения.
Брусья классифицируются по форме поперечного сечения и форме оси.
По форме поперечного сечения различают брусья постоянного сечения и переменного
сечения. По форме оси – прямолинейные и криволинейные брусья.
Примерами прямых брусьев являются балки и стержни мостовых и козловых кранов,
валы редукторов и коробок передач, оси транспортных средств.
Примерами кривых брусьев служат грузоподъёмные крюки, звенья сварных цепей,
струбцины, коленчатые валы, станины станков.

6.

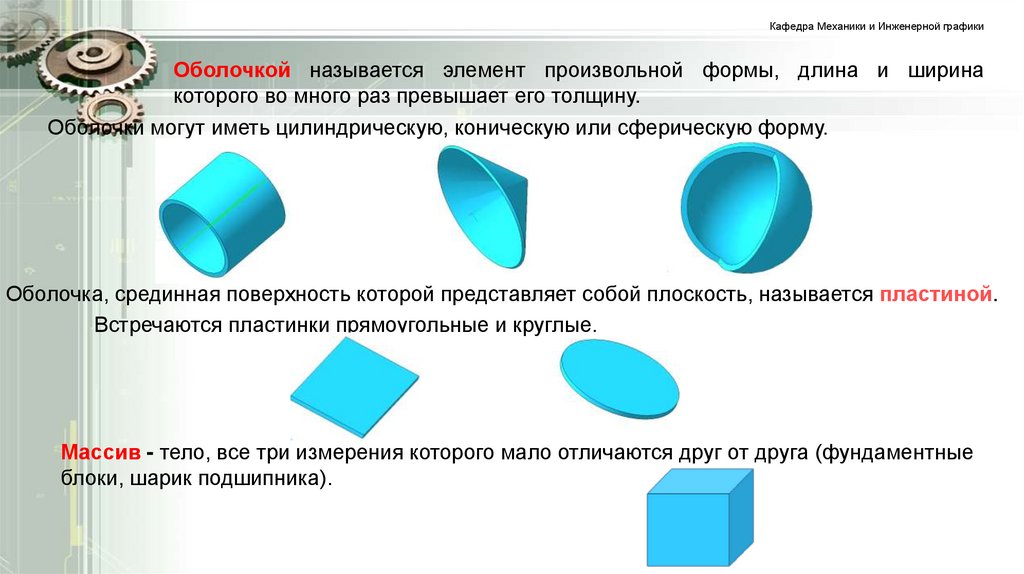
Кафедра Механики и Инженерной графики
Оболочкой называется элемент произвольной формы, длина и ширина
которого во много раз превышает его толщину.
Оболочки могут иметь цилиндрическую, коническую или сферическую форму.
Оболочка, срединная поверхность которой представляет собой плоскость, называется пластиной.
Встречаются пластинки прямоугольные и круглые.
Массив - тело, все три измерения которого мало отличаются друг от друга (фундаментные
блоки, шарик подшипника).

7.

Кафедра Механики и Инженерной графики
Основные гипотезы сопротивления материалов
1. Материал считается однородным, если его свойства во всех точках одинаковы.
2. Материал считается изотропным, если его свойства во всех направлениях одинаковы
(Изотропными являются аморфные материалы, такие как стекло и смолы. Анизотропными
являются пластмассы, текстолит и т.п.).
3. Материал обладает свойством идеальной упругости, вследствие которой
деформируемое тело полностью восстанавливает свою форму и размеры после снятия
нагрузки независимо от величин нагрузок и температуры тела.
4. Форма и размеры упругого тела меняются прямо пропорционально изменению
нагрузок, то есть подчиняется закону Гука (1660 г.).
5. Материал обладает свойством сплошности, то есть способностью сплошь (без пустот)
заполнять пространство, ограниченное поверхностью тела. Вследствие этого материал
считается непрерывным, что позволяет использовать для определения напряжений и
деформаций математический аппарат дифференциального и интегрального исчисления.
6. Упругие тела являются относительно жесткими, благодаря чему перемещения точек тела
весьма малы по сравнению с размерами самого тела. Эта гипотеза служит основанием
для использования при расчете начальных (исходных) размеров тела (по
недеформированной схеме).

8.

Кафедра Механики и Инженерной графики
Вопрос 2. Метод сечений
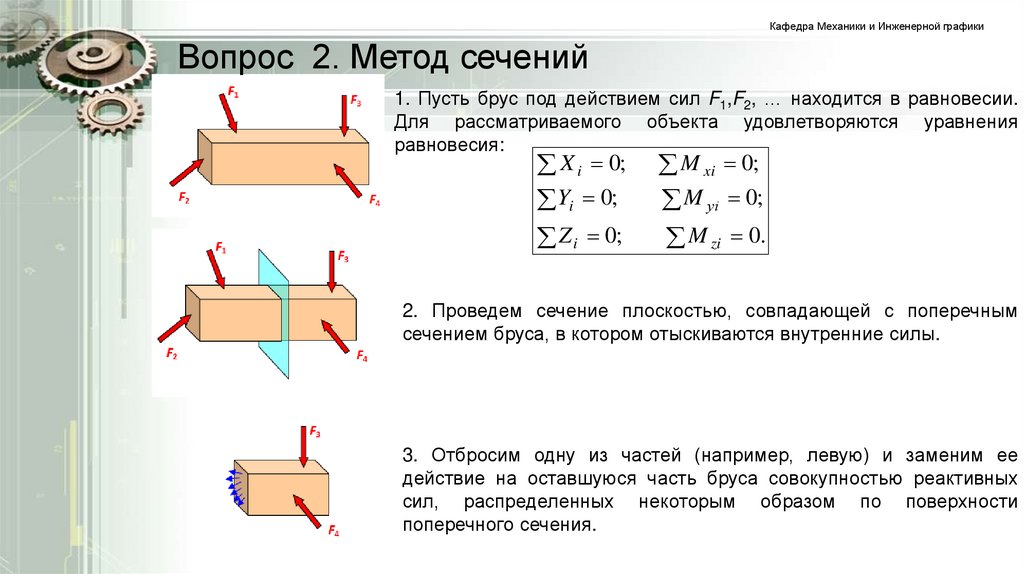
1. Пусть брус под действием сил F1,F2, … находится в равновесии.
Для рассматриваемого объекта удовлетворяются уравнения
равновесия:
X i 0;
Yi 0;
Z i 0;
M xi 0;
M уi 0;
M zi 0.
2. Проведем сечение плоскостью, совпадающей с поперечным
сечением бруса, в котором отыскиваются внутренние силы.
3. Отбросим одну из частей (например, левую) и заменим ее
действие на оставшуюся часть бруса совокупностью реактивных
сил, распределенных некоторым образом по поверхности
поперечного сечения.

9.

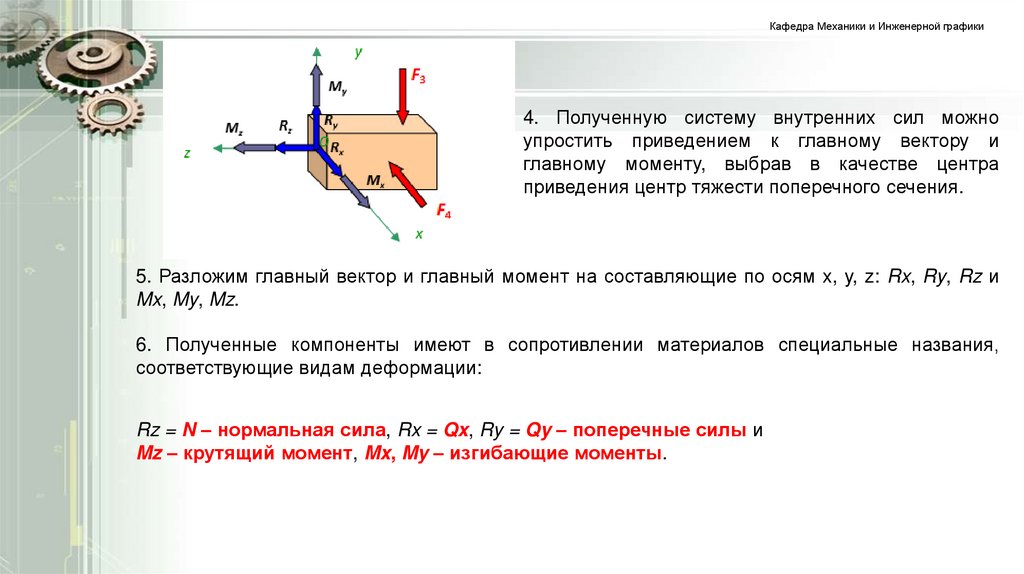
Кафедра Механики и Инженерной графики
4. Полученную систему внутренних сил можно
упростить приведением к главному вектору и
главному моменту, выбрав в качестве центра
приведения центр тяжести поперечного сечения.
5. Разложим главный вектор и главный момент на составляющие по осям x, y, z: Rx, Ry, Rz и
Mx, My, Mz.
6. Полученные компоненты имеют в сопротивлении материалов специальные названия,
соответствующие видам деформации:
Rz = N – нормальная сила, Rx = Qx, Ry = Qy – поперечные силы и
Mz – крутящий момент, Mx, My – изгибающие моменты.

10.

Кафедра Механики и Инженерной графики
7. Поскольку оставленная часть бруса должна остаться в равновесии, полученные
внутренние силовые факторы могут быть определены: из уравнений равновесия,
составленных для этой части:
Qx X i
оставл.части
Q y Yi
оставл.части
N Zi
оставл.части
0;
0;
0;
оставл.части
0;
оставл.части
0;
оставл.части
0.
M x M xi
M y M уi
M z M zi

11.

Кафедра Механики и Инженерной графики
Деформированные состояния, при которых возникают
данные силовые факторы:
1. Растяжение-сжатие (продольные силы N);
2. Сдвиг (поперечные силы Qx , Q y );
3. Кручение (крутящий момент M к );
4. Изгиб (изгибающие моменты M x , M y );
5. Сложные деформации (несколько усилий, например,
изгибающий и крутящий моменты).

12.

Кафедра Механики и Инженерной графики
Напряжение – мера, характеризующая распределение внутренних сил
по сечению.
Поскольку внутренние силы, представляют собой поверхностные силы, приложенные к
поперечному сечению оставленной части, то интенсивность этих сил, называемое полным
напряжением, определяется как :
y
R
ny
p lim
p
n
σ
A 0 A
n
n
Размерность этого напряжения совпадает с размерностью
поверхностной нагрузки (Н/м2, МПа = 106 Н/м2).
z
nx
x
Полное напряжение, как и равнодействующая внутренних сил, приложенных на
элементарной площадке, является векторной величиной и может быть разложено на две
составляющие: перпендикулярное к рассматриваемой площадке – нормальное
напряжение σn и касательное к площадке – касательное напряжение n.
Касательное напряжение, в свою очередь, может быть разложено на две
составляющие, параллельные координатным осям x, y, связанным с поперечным сечением nx , ny .

13.

Вопрос 3. Центральное растяжение-сжатие.
Растяжение-сжатие - вид деформации стержня (бруса)
или его части под действием продольных (растягивающих или
сжимающих) сил
Правило знаков для продольной силы: растягивающие
продольные силы (направленные от сечения) считаются
положительными, сжимающие (направленные к сечению) –
отрицательными.
Эпюрой продольной силы называется график, показывающий
изменение продольной силы по оси стержня.

14.

Кафедра Механики и Инженерной графики
При растяжении (сжатии) в поперечном сечении стержня
= N
F
При растяжении нормальные напряжения – положительные, при
сжатии – отрицательные.
Изменение длины стержня l l1 l называют линейной продольной
деформацией (абсолютным удлинением);
изменение поперечного сечения a a1 a
- линейной поперечной
деформацией.

15.

Кафедра Механики и Инженерной графики
Интенсивность
деформирования
оценивают
деформациями, приходящимися на единицу длинны
стержня: относительной продольной
и
относительной поперечной :
l
l
a
a
Отношение поперечной деформации к продольной
называется коэффициентом Пуассона :
0,2
0,5.

16.

Кафедра Механики и Инженерной графики
N l
l
E F
ЗАКОН ГУКА:
где
l - абсолютная продольная деформация;
N – продольная сила;
F – площадь поперечного сечения;
E – модуль продольной упругости (модуль Юнга).
Закон Гука можно преобразовать, учитывая определения
N
внутреннего напряжения (
F ) и относительной
деформации (
l
l
):
= E·

17.

Кафедра Механики и Инженерной графики
Максимальные напряжения при растяжении (сжатии):
max = N max
F
Условие прочности: max
Условие жесткости: max
Условие жесткости при растяжении (сжатии) можно
записать и в другом виде:
lmax = N max l l
E F

18.

Кафедра Механики и Инженерной графики
Вопрос 3. Определение внутренних усилий
Внутренние усилия определяются методом сечений в совокупности точек по длине бруса
с целью обнаружения их максимальных значений. График изменения внутреннего усилия по
оси бруса называется эпюрой.
Общий порядок построения эпюр внутренних усилий:
1. Если необходимо, то определяются опорные реакции так, как это делается в курсе
теоретической механики (выбрать объект, отбросить связи, заменить отброшенные связи
реакциями, составить уравнения равновесия). Реакции можно не находить, если они не
входят в число внешних сил, приложенных по одну сторону от рассматриваемых сечений.
2. Определяется число участков по длине бруса, на которых нагрузка или геометрия бруса
не изменяется. Границей участка является любой фактор, влияющий на резкое
(скачкообразное) изменение рассматриваемого внутреннего усилия (начало или конец бруса,
перелом оси бруса, место расположения опоры, точка приложения внешней
сосредоточенной силы или другого фактора, например, сосредоточенного момента, начало
или конец распределенной нагрузки).

19.

Кафедра Механики и Инженерной графики
3. На каждом из участков проводится сечение, отстоящее от начала участка на некотором
произвольном (переменном) расстоянии. Для каждого сечения указывается текущая
координата (z) от начала участка или от начала бруса и записываются пределы изменения
координаты. При выборе начала локальных координат в начале участка нижний предел
всегда равен нулю.
4. Для рассматриваемого сечения определяется выражение внутреннего усилия в функции
от координаты z рассмотрением равновесия оставленной части или используя
установленные определения для вычисления внутреннего усилия по внешним силам,
расположенным по одну сторону от сечения.
По полученным выражениям строится эпюра изменения усилия подстановкой верхнего
и нижнего пределов, и если необходимо, других значений координат в разрешенном
интервале, обычно в середине интервала.
5.

20.

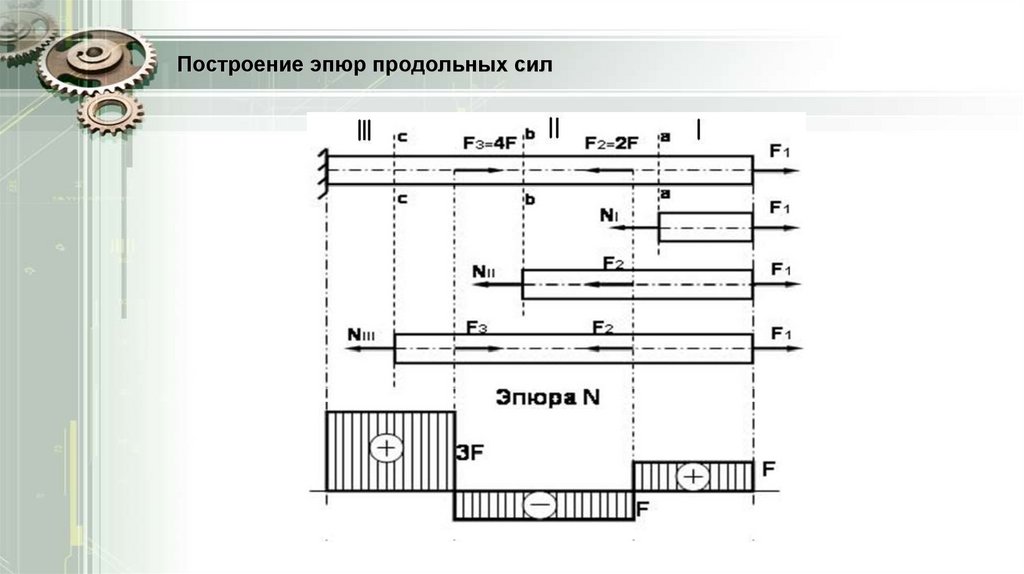
Построение эпюр продольных сил
Построить эпюру продольных сил для бруса, если:
F1=F, F2=2F, F3=4F
Проводя произвольно сечение а-а на участке I,
составляем уравнение равновесия:
F - NI = 0
Z = 0
N I = F (растяжение)

21.

Построение эпюр продольных сил
Проводим сечение b-b на участке II:
Z = F - F - N
1
2
II
= F - 2F - N II = 0
N II = - F (сжатие)

22.

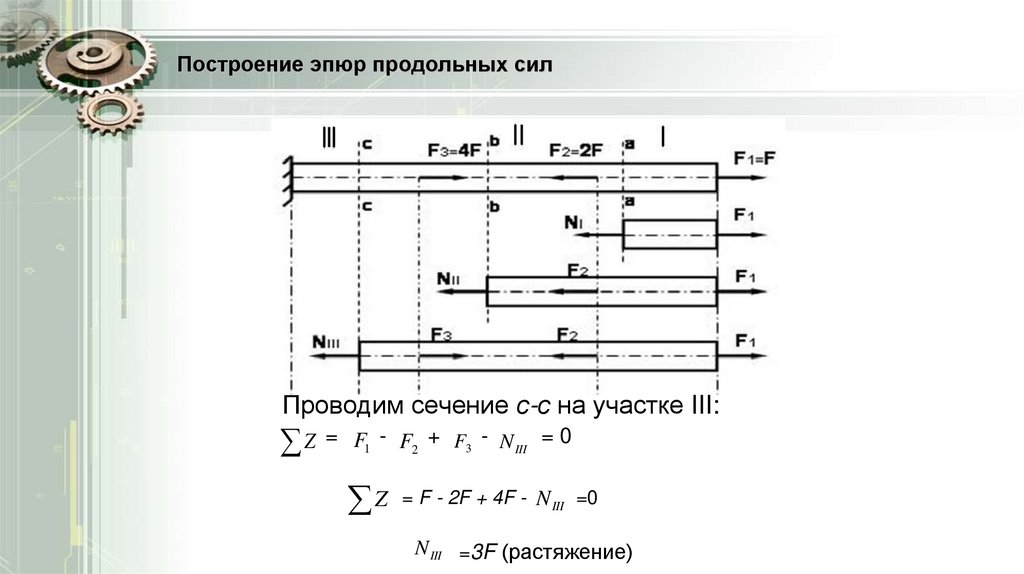
Построение эпюр продольных сил
Проводим сечение с-с на участке III:
Z = F - F + F - N
1
2
3
III
=0
Z = F - 2F + 4F - N
III
=0
N III =3F (растяжение)

23.

Построение эпюр продольных сил

24.

Лекция закончена.
Спасибо за внимание!
© САНКТ-ПЕТЕРБУРГСКИЙ УНИВЕРСИТЕТ ГПС МЧС РОССИИ, IGPS.RU, 2020.
24