Похожие презентации:
Основные понятия и определения сопротивления материалов. Закон Гука при центральном растяжении
1. СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ Тема 3.1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ Занятие 3.1.2. Закон Гука при
центральном растяжении (сжатии)2.
Учебные вопросы:1. Построение эпюр продольных сил.
2. Абсолютная и относительная
продольная деформация. Коэффициент
Пуассона.
3. Закон Гука.
3.
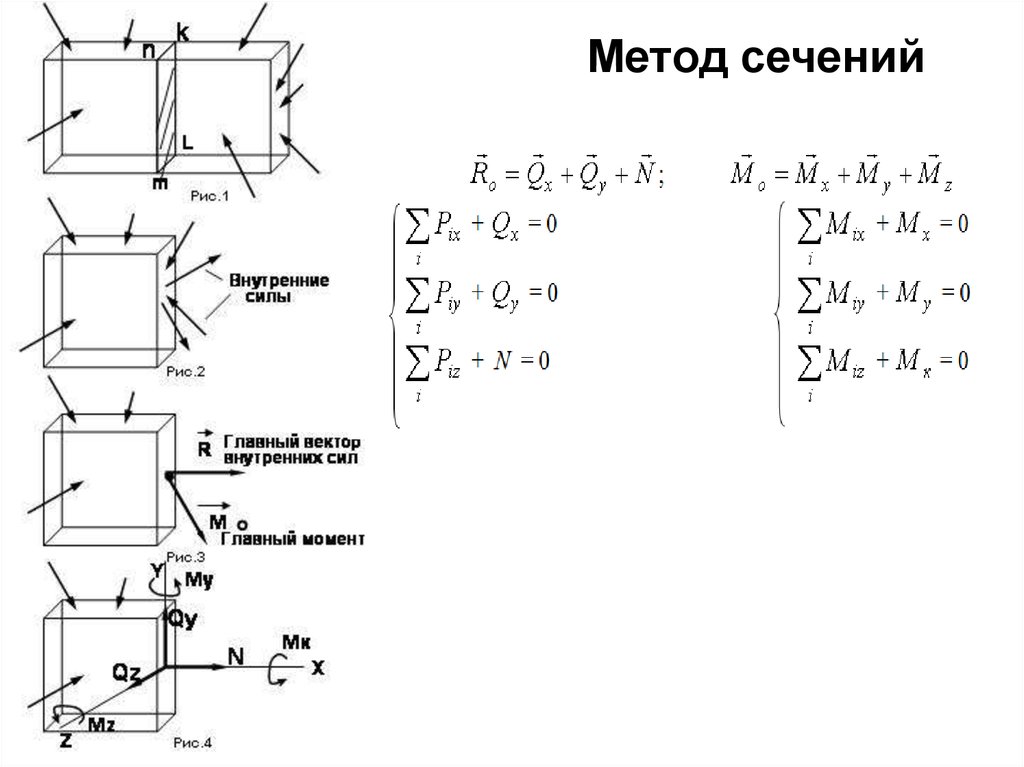
Метод сечений4.
Q x , Q y , Q z , M x, M y , M z M к называются• Составляющие
внутренними силовыми факторами.
• Здесь Pix , Piy , Piz
– суммы проекций всех
i
i
i
внешних сил;
M , M , M
ix
i
iy
i
iz
– суммы проекций внешних моментов;
i
N – продольная сила;
Qx , Qy - поперечные силы;
M z M к - крутящий момент;
M x , M y - изгибающие моменты.
5. Деформированные состояния, при которых возникают данные силовые факторы:
1. Растяжение-сжатие (продольные силы N);2. Сдвиг (поперечные силы Qx , Q y );
3. Кручение (крутящий момент M к );
4. Изгиб (изгибающие моменты M x , M y );
5. Сложные деформации (несколько усилий,
например, изгибающий и крутящий
моменты).
6.
Правило знаков для продольной силы:растягивающие продольные силы
(направленные от сечения) считаются
положительными, сжимающие
(направленные к сечению) –
отрицательными.
Эпюрой продольной силы называется
график, показывающий изменение
продольной силы по оси стержня.
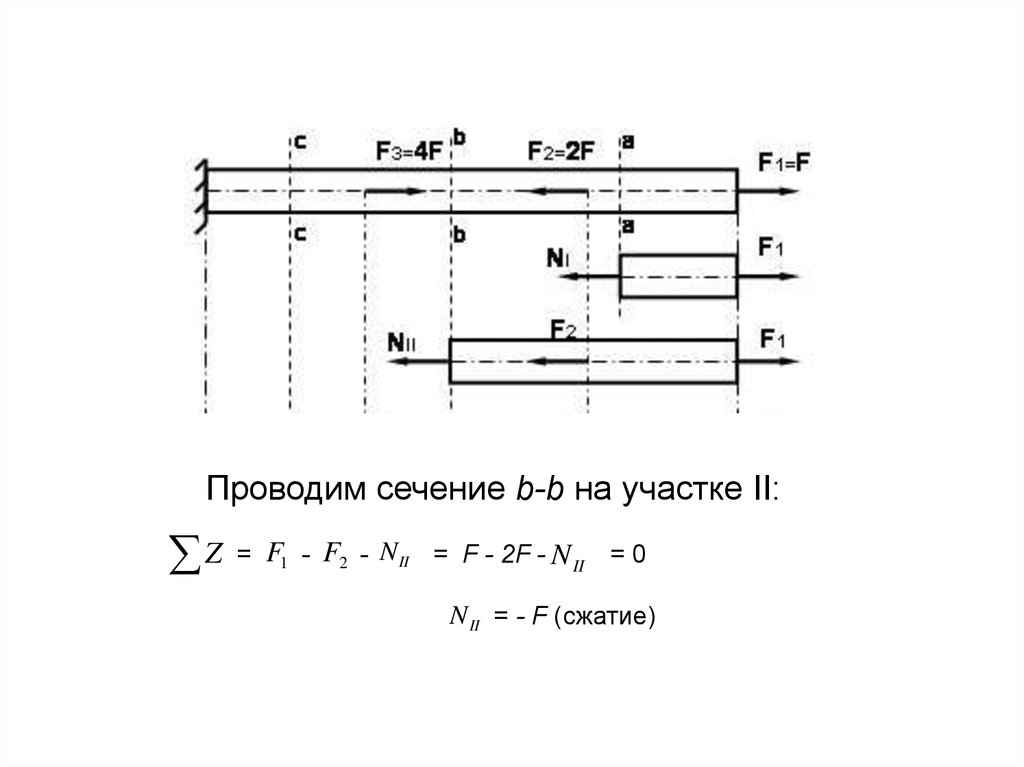
7. Пример
Построить эпюру продольных сил для бруса, если:F1=F, F2=2F, F3=4F
Проводя произвольно сечение а-а на участке I, составляем
уравнение равновесия:
F - NI = 0
Z = 0
N I = F (растяжение)
8.
Проводим сечение b-b на участке II:Z
= F1 - F2 - N II = F - 2F - N II = 0
N II = - F (сжатие)
9.
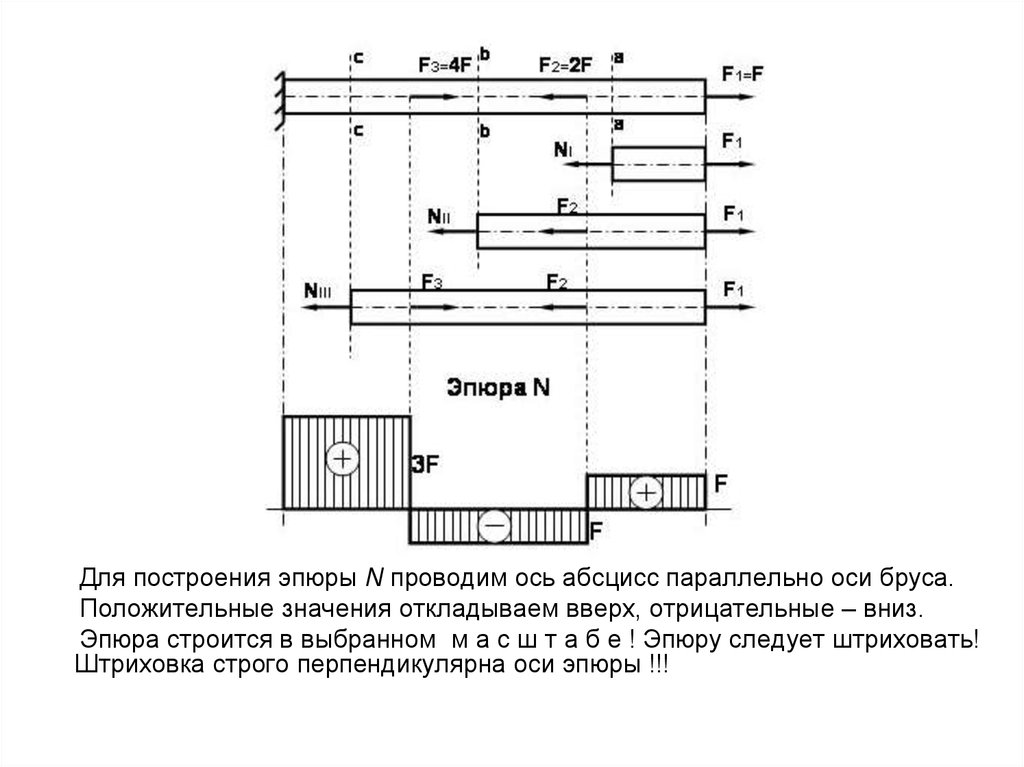
Проводим сечение с-с на участке III:Z
= F1 - F2 + F3 - N III = 0
Z
= F - 2F + 4F - N III =0
N III =3F (растяжение)
10.
Для построения эпюры N проводим ось абсцисс параллельно оси бруса.Положительные значения откладываем вверх, отрицательные – вниз.
Эпюра строится в выбранном м а с ш т а б е ! Эпюру следует штриховать!
Штриховка строго перпендикулярна оси эпюры !!!
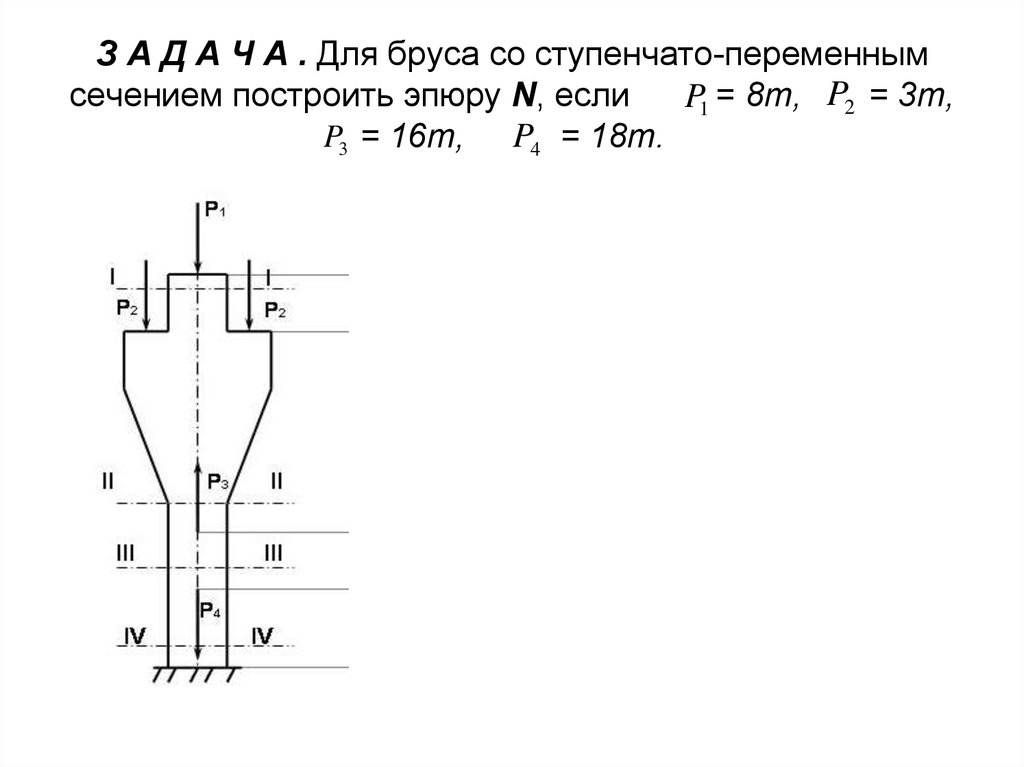
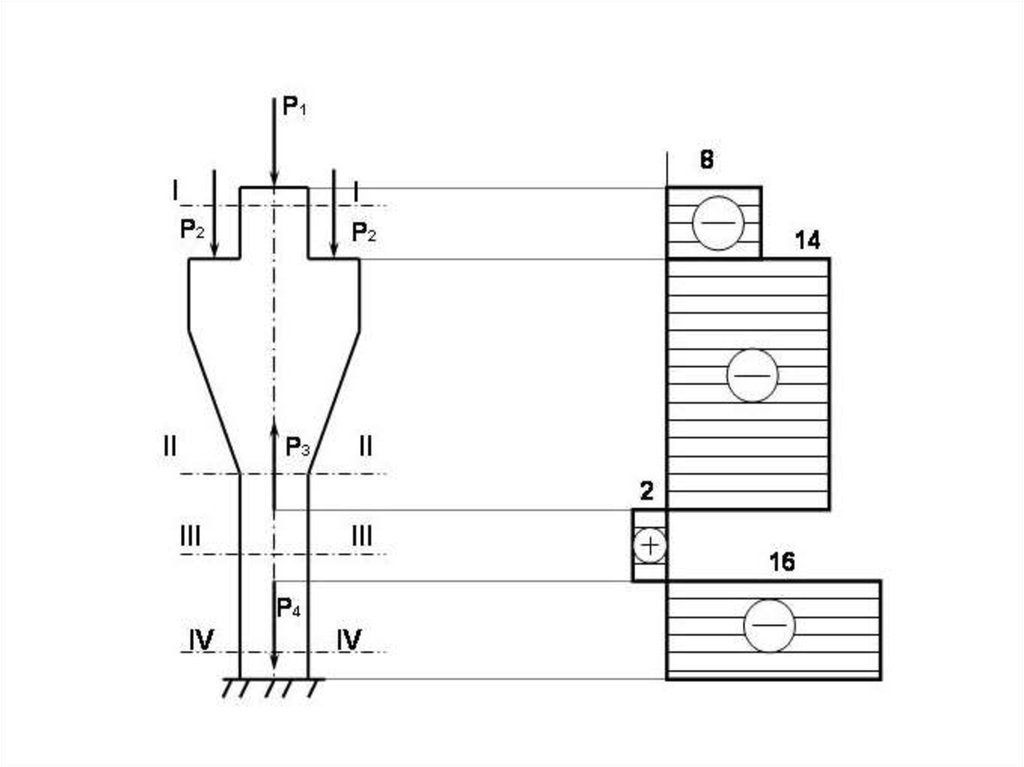
11. З А Д А Ч А . Для бруса со ступенчато-переменным сечением построить эпюру N, если = 8т, = 3т, = 16т, = 18т.
З А Д А Ч А . Для бруса со ступенчато-переменнымсечением построить эпюру N, если
P1 = 8т, P2 = 3т,
P3 = 16т, P4 = 18т.
12.
13. Абсолютная и относительная продольная деформация. Коэффициент Пуассона.
• Напряжение – это внутренняя сила, приходящаясяна единицу площади:
=
P
F
Единицы измерения напряжения:
2
6
2
м
мм
10
1 Па = 1 Н/ ; 1 МПа =
Па =1 Н/
Допускаемые напряжения ( и – нормальные и
касательные) – это такие максимальные напряжения,
при которых не происходит разрушение данной
конкретной детали, и она работает в условиях
упругих деформаций.
14.
При растяжении (сжатии) в поперечном сечениистержня
P
N
=F = F
При растяжении нормальные напряжения –
положительные, при сжатии – отрицательные.
Изменение длины стержня l l1 l называют
линейной продольной деформацией (абсолютным
удлинением);
изменение поперечного сечения a a1 a - линейной
поперечной деформацией.
15.
Интенсивность деформирования оцениваютдеформациями, приходящимися на единицу длинны
стержня: относительной продольной и
относительной поперечной :
a
a
l
l
Деформации бывают продольные и поперечные.
Отношение поперечной деформации к продольной
называется коэффициентом Пуассона :
0,2
0,5.
16. Закон Гука
P ll
E F
где
l - абсолютная продольная деформация;
P – осевая внешняя сила;
F – площадь поперечного сечения;
E – модуль продольной упругости (модуль Юнга).
Закон Гука можно преобразовать, учитывая определения
N
внутреннего напряжения (
= ) и относительной
ЗАКОН ГУКА (открыт в 1660):
F
l
деформации ( l ):
= E·
17.
Максимальные напряжения при растяжении (сжатии):max = N max
F
Условие прочности: max
Условие жесткости: max
Условие жесткости при растяжении (сжатии) можно
записать и в другом виде:
lmax = N max l l
E F
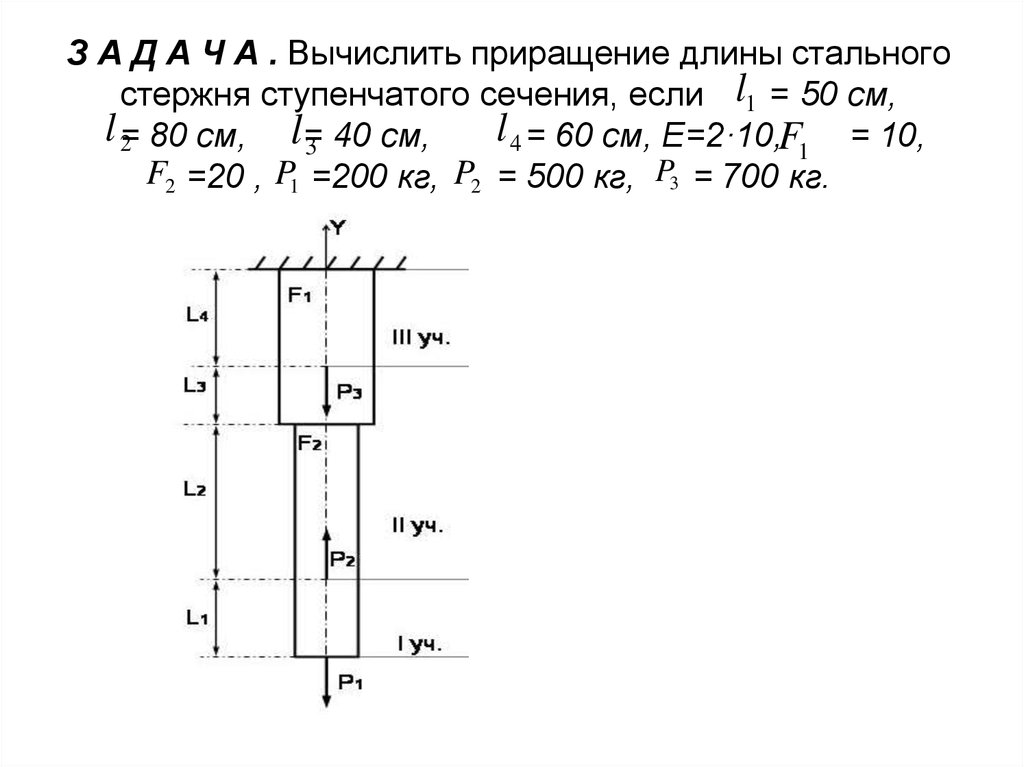
18. З А Д А Ч А . Вычислить приращение длины стального стержня ступенчатого сечения, если = 50 см, = 80 см, = 40 см, = 60 см,
З А Д А Ч А . Вычислить приращение длины стальногостержня ступенчатого сечения, если l1 = 50 см,
l =2 80 см, l=3 40 см,
l 4 = 60 см, Е=2·10,F1 = 10,
F2 =20 , P1 =200 кг, P2 = 500 кг, P3 = 700 кг.
19.
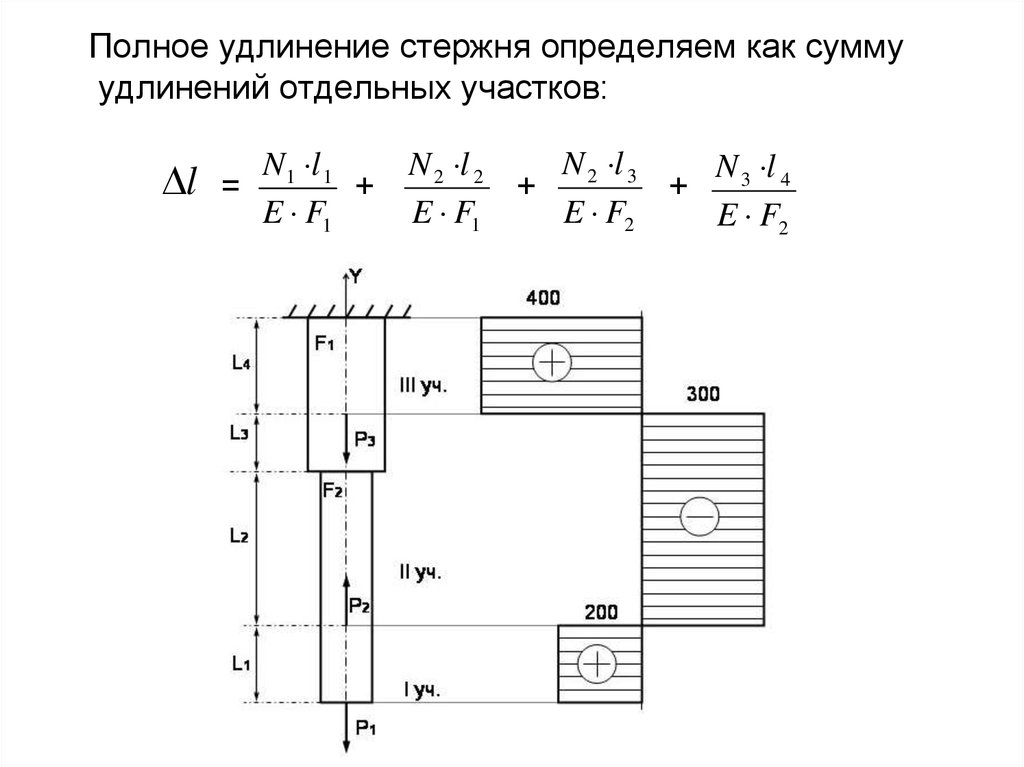
Полное удлинение стержня определяем как суммуудлинений отдельных участков:
l
N 1 l 1
=
+
E F1
N 2 l 3
N 2 l 2
N 3 l 4
+
+
E F1
E F2
E F2












 Механика
Механика








