Операции над отношениями. Реляционная алгебра. Реляционное исчисление. Теоретико-множественные операции реляционной алгебры

1.

19. Операции над отношениями.
Реляционная алгебра. Реляционное
исчисление. Теоретикомножественные операции
реляционной алгебры.
1

2.

ЯЗЫК УПРАВЛЕНИЯ ДАННЫМИ
Языки
DML(Data
Manipulation
Language) различаются базовыми
конструкциями извлечения данных.
Различают два типа языков:
процедурный и непроцедурный.
2

3.

С помощью процедурного языка
можно указать, какие данные
необходимы, и как их можно
получить.
Языки сетевых и иерархических
СУБД
обычно
бывают
процедурными.
3

4.

Непроцедурный
язык
позволяет указать лишь то,
какие данные необходимо
получить, без указания на то,
как их следует извлекать.
4

5.

В реляционных СУБД для выполнения
операций над отношениями используются 2
группы языков, имеющие в качестве своей
математической основы теоретические языки
запросов, предложенные Э.Коддом.
• Реляционная алгебра (процедурный)
• Реляционное исчисление
(непроцедурный)
5

6.

Реляционная
алгебра
как
теоретический язык запросов более
наглядно описывает выполняемые над
отношениями действия.
В
реляционной
алгебре
операнды и результаты всех
действий
являются
отношениями.
6

7.

В
реализациях
конкретных
реляционных СУБД сейчас не
используется в чистом виде ни
реляционная
алгебра,
ни
реляционное исчисление.
Фактическим
стандартом
доступа
к
реляционным
данным стал язык SQL.
7

8.

Язык SQL представляет собой смесь
операторов реляционной алгебры и
выражений
реляционного
исчисления,
использующий
синтаксис, близкий к фразам
английского языка и расширенный
дополнительными возможностями,
отсутствующими в реляционной
алгебре и реляционном исчислении.
8

9.

.
Таким образом, реляционный оператор
выглядит как функция с отношениями в
качестве
аргументов,
возвращающая
отношение в качестве результата:
9

10.

Реляционная алгебра является замкнутой,
т.к. в качестве аргументов в реляционные
операторы можно подставлять другие
реляционные операторы, подходящие по
типу:
Таким образом, в реляционных выражениях можно использовать
вложенные выражения сколь угодно сложной структуры.
10

11.

Операции над отношениями
Операции над отношениями можно разделить
на 2 группы.
Первую группу составляют операции над
множествами, к которым относятся операции
объединения, пересечения, разности,
деления и декартова произведения.
Вторую группу составляют специальные
операции над отношениями, к
которым
относятся
проекция,
соединение,
выборка.
11

12.

Операции реляционной алгебры могут
выполняться над одним отношением
(например, проекция) или над двумя
отношениями (объединение). В первом
случае операция называется унарной, во
втором - бинарной.
Например, при выполнении бинарной
операции пересечения, объединения,
разности отношения должны быть
совместимы
по
структуре.
Совместимость по структуре означает
совместимость имён атрибутов и типов
соответствующих доменов.
12

13.

Некоторые отношения не являются
совместимыми
по
структуре,
но
становятся таковыми после некоторого
переименования атрибутов. Для того
чтобы такие отношения можно было
использовать
в
реляционных
операторах, вводится вспомогательный
оператор
переименования
атрибутов.
13

14.

Оператор переименования атрибутов
Оператор переименования атрибутов
имеет следующий синтаксис:
где
R- отношение,
Atr1, Atr2… - исходные имена атрибутов,
AtrNew1, AtrNew2- новые имена атрибутов.
В результате применения оператора
переименования
атрибутов
получаем
новое
отношение,
с
изменёнными
именами атрибутов.
14

15.

Теоретико-множественные
операторы
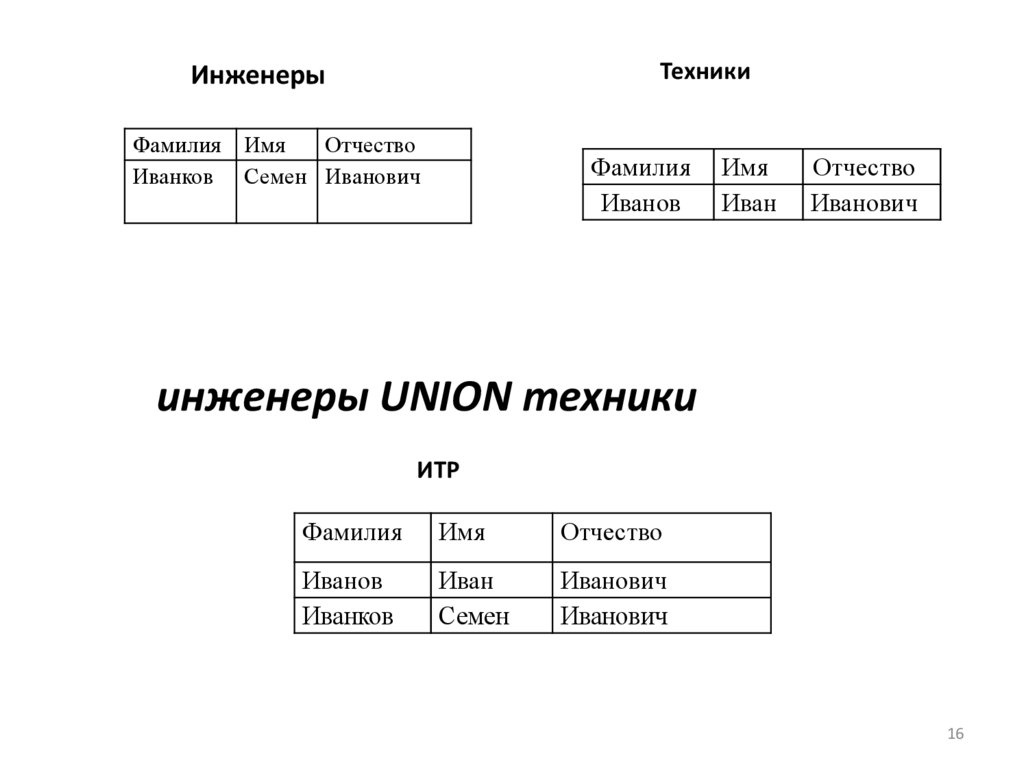
Объединение.
Объединением отношений R1 и R2
R1 UNION R2,
имеющих одинаковый набор атрибутов,
называют отношение R, содержащее все
кортежи,
входящие
в
исходные
отношения
(с
исключением
повторений).
15

16.

Техники
Инженеры
Фамилия
Иванков
Имя
Отчество
Семен Иванович
Фамилия
Иванов
Имя
Иван
Отчество
Иванович
инженеры UNION техники
ИТР
Фамилия
Имя
Отчество
Иванов
Иванков
Иван
Семен
Иванович
Иванович
16

17.

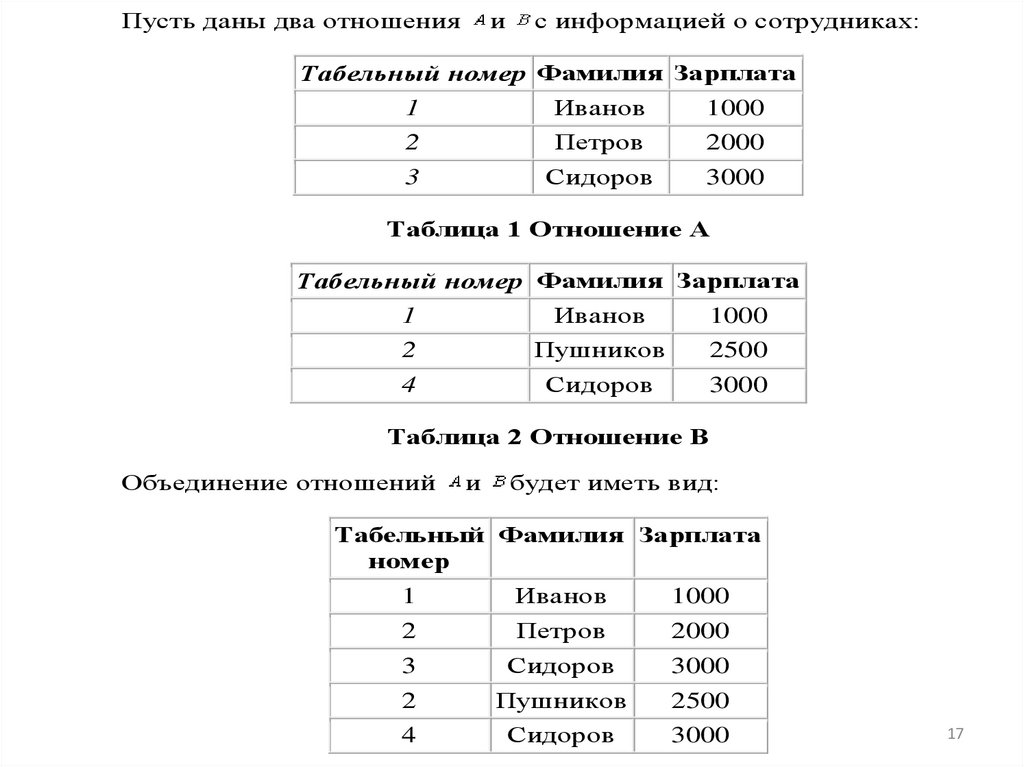
Пусть даны два отношения
и
с информацией о сотрудниках:
Табельный номер Фамилия Зарплата
1
Иванов
1000
2
Петров
2000
3
Сидоров
3000
Таблица 1 Отношение A
Табельный номер Фамилия Зарплата
1
Иванов
1000
2
Пушников
2500
4
Сидоров
3000
Таблица 2 Отношение B
Объединение отношений
и
будет иметь вид:
Табельный Фамилия Зарплата
номер
1
Иванов
1000
2
Петров
2000
3
Сидоров
3000
2
Пушников
2500
4
Сидоров
3000
17

18.

Как видно из приведённого примера,
потенциальные ключи, которые были в
отношениях не наследуются объединением
этих отношений. Поэтому, в объединении
отношений атрибут "Табельный номер" может
содержать дубликаты значений.
Объединение отношений имеет, как и любое
отношение, потенциальный ключ, например,
состоящий из всех атрибутов.
18

19.

Пересечение
Пересечением двух совместимых по
структуре отношений R1 и R2, называется
отношение R с тем же заголовком, что и у
отношений R1 и R2 и содержащее строки
принадлежащие
и
R1
и
R2.
R1 INTERSECT R2
Для тех же отношений и , что и в предыдущем примере
пересечение имеет вид:
Табельный номер Фамилия Зарплата
1
Иванов
1000
19

20.

Разность отношений
Разностью отношений R1 и R2
R1 MINUS R2,
совместимых по структуре называют
отношение R, содержащее все строки,
принадлежащие
R1,
но
не
принадлежащие R2.
20

21.

А
Табельный номер Фамилия Зарплата
1
Иванов
1000
2
Петров
2000
3
Сидоров
3000
B
Табельный номер Фамилия Зарплата
1
Иванов
1000
Пушников
2
2500
Табельный номер Фамилия Зарплата
2
Петров
2000
3
Сидоров
3000
Отношение A MINUS B
21

22.

Произведение отношений
Произведением отношения R1 степени* к1 и R2
степени к2
R1 TIMES R2,
которые не имеют одинаковых атрибутов,
называется отношение R степени к1+к2,
заголовок которого представляет сцепление
заголовков отношений R1 и R2, а тело содержит
кортежи, полученные сцеплением каждого
кортежа отношения R1 с каждым кортежем
отношения R2.
*Степень отношения – количество атрибутов,
входящих в его схему.
.
22

23.

Мощность (число кортежей)
отношения
R
равна
произведению
мощностей
отношений R1 и R2.
Перемножать
можно
любые
отношения,
совместимость
два
по
типу при этом не требуется.
23

24.

Пример.
Пусть
отношение
R1
представляет собой множество номеров
всех текущих поставщиков, а отношение
R2 – множество номеров всех текущих
деталей.
Результатом операции будет множество
всех пар «Поставщик-деталь».
24

25.

Операция обычно используется для получения
отношения, которое характеризует
все возможные комбинации между элементами
отдельных отношений.
Однако самостоятельного
значения результат операции не имеет,
а участвует в дальнейшей обработке
25

26.

Деление
R1 DEVIDE BY R2
Деление выполняется над отношениями,
одно из которых - делитель должно
содержать
подмножество
атрибутов
отношения - делимого.
Результирующее отношение содержит
только те атрибуты делимого, которых нет
в делителе, и включает только те кортежи,
декартовы произведения с делителем
которых содержатся в делимом.
26

27.

Типичные
запросы,
реализуемые
с
помощью операции деления, обычно в
своей формулировке имеют слово "все«,
например, "Какие поставщики поставляют
все детали?".
27

28.

Пример.
В
качестве
делимого
возьмём
отношение,
содержащее
номера
поставщиков и номера поставляемых
ими деталей:
28

29.

29

30.

Даны отношения R1 и R2.
R1
R2
Преподаватель Группа
Иванов
Федоров
Иванов
Иванов
Смирнов
Федоров
11
11
12
13
11
12
Группа
11
12
13
Какое значение будет содержать отношение.
полученное в результате выполнения: R1 DEVIDE
BY R2 ?
30

31.

Проекция
R[x,y,…z]
Проекция отношения R на атрибуты
x,y,…z (где x,y,…z – подмножество
полного списка атрибутов заголовка R)
представляет собой отношение R1 с
заголовком x,y,…z и телом содержащим
кортежи отношения R за исключением
повторяющихся кортежей.
31

32.

Операция
проекции
дает
"вертикальный
срез"
отношения, в котором удалены
все возникшие при таком срезе
дубликаты кортежей.
32

33.

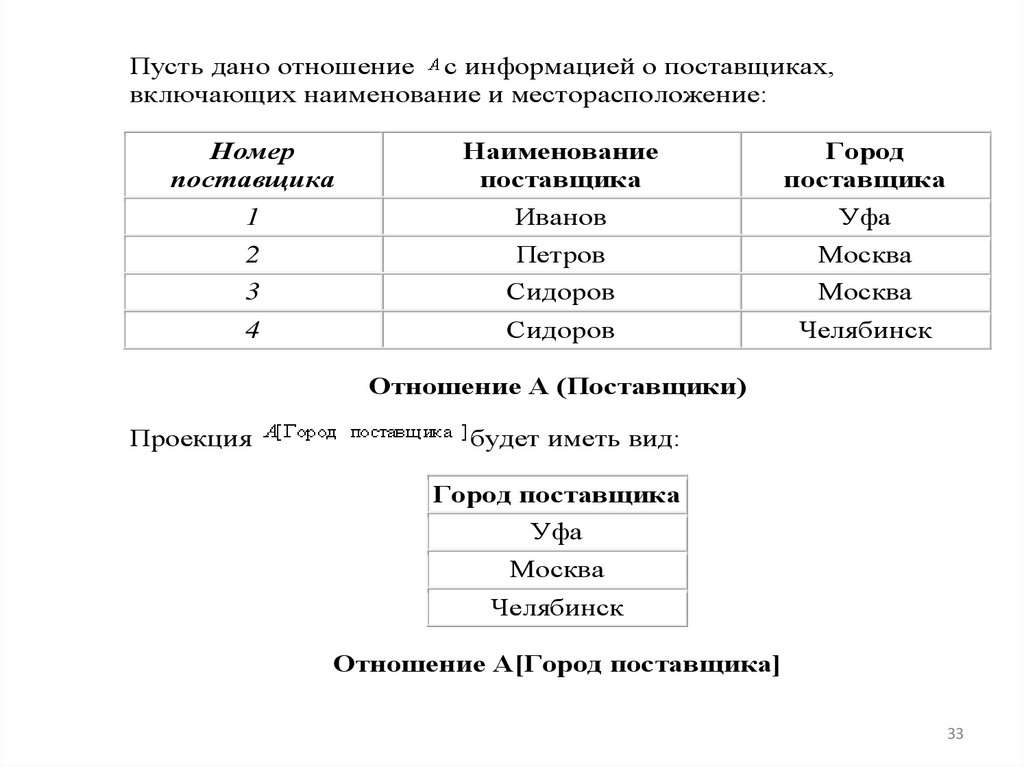
Пусть дано отношение с информацией о поставщиках,
включающих наименование и месторасположение:
Номер
поставщика
1
Наименование
поставщика
Город
поставщика
Иванов
Уфа
2
Петров
Москва
3
Сидоров
Москва
4
Сидоров
Челябинск
Отношение A (Поставщики)
Проекция
будет иметь вид:
Город поставщика
Уфа
Москва
Челябинск
Отношение A[Город поставщика]
33

34.

Выборка
В результате выборки из отношения R
получается новое отношение R1 с
таким
же
заголовком,
кортежи
которого удовлетворяют истинности
логического выражения f.
R WHERE f
Для записи f используются имена
атрибутов,
константы,
логические
операции, операции сравнения и
скобки.
34

35.

Пусть дано отношение с информацией о сотрудниках:
Табельный номер Фамилия Зарплата
1
Иванов
1000
2
Петров
2000
3
Сидоров
3000
Табельный номер Фамилия Зарплата
1
Иванов
1000
2
Петров
2000
Таким образом, операция выборки дает
"горизонтальный срез" отношения по некоторому
условию.
35

36.

Cоединение
Соединение отношений R1 и R2 по
условию, заданному формулой f,
представляет собой отношение R,
которое
можно
получить
путем
Декартова произведения отношений R1
и R2 c последующим применением к
результату выборки по формуле f.
(R1 TIMES R2) WHERE f
36

37.

Важными с практической точки
зрения
частными
случаями
соединения
являются
эквисоединение и естественное
соединение.
Операция
эквисоединения
характеризуется тем, что формула
f задает равенство операндов.
37

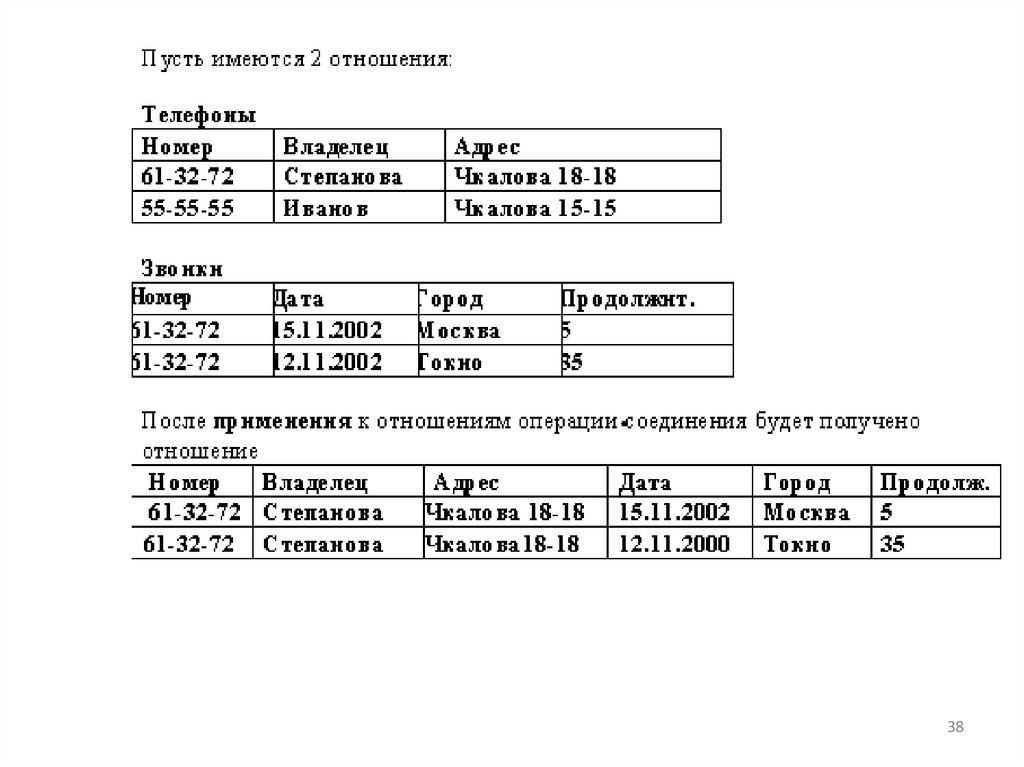
38.

38

39.

( Телефоны TIMES Звонки) WHERE
Телефоны.Номер=Звонки.Номер
39

40.

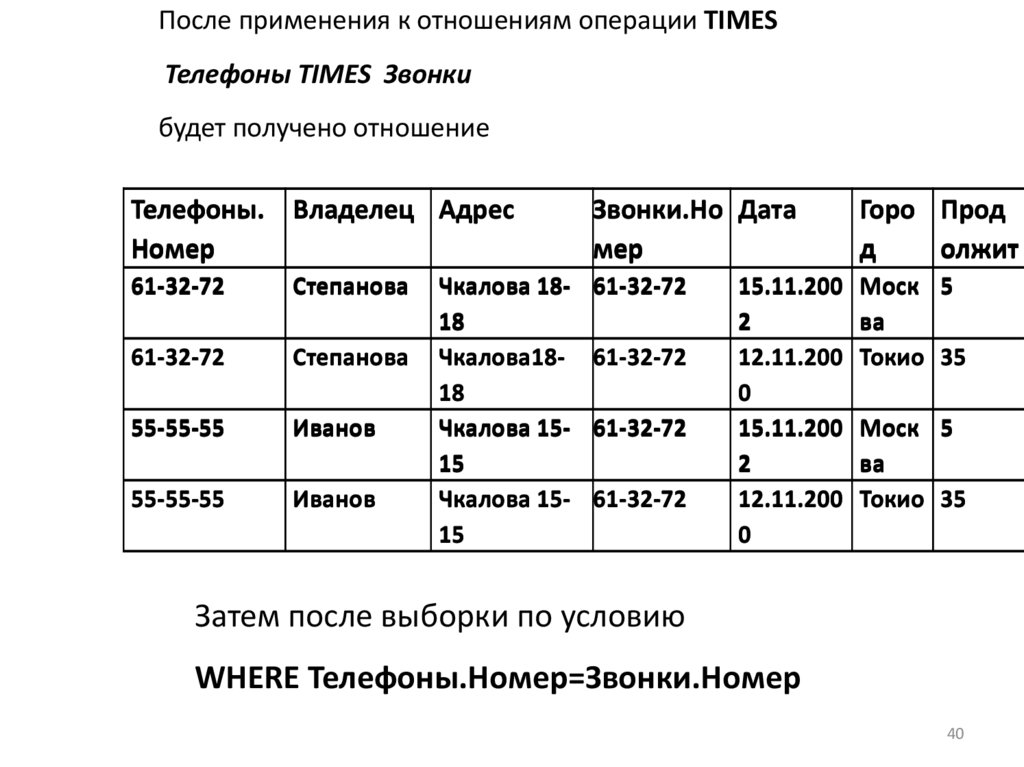
После применения к отношениям операции TIMES
Телефоны TIMES Звонки
будет получено отношение
Телефоны. Владелец Адрес
Номер
Звонки.Но Дата
мер
61-32-72
Степанова
61-32-72
61-32-72
Степанова
55-55-55
Иванов
55-55-55
Иванов
Чкалова 1818
Чкалова1818
Чкалова 1515
Чкалова 1515
61-32-72
61-32-72
61-32-72
Горо Прод
д
олжит
15.11.200 Моск 5
2
ва
12.11.200 Токио 35
0
15.11.200 Моск 5
2
ва
12.11.200 Токио 35
0
Затем после выборки по условию
WHERE Телефоны.Номер=Звонки.Номер
40

41.

( Телефоны TIMES Звонки) WHERE
Телефоны.Номер=Звонки.Номер
Телефоны. Владелец
Номер
Адрес
Звонки.Номер Дата
Город Продолжит
1- -
Степанова
Чкалова
18-18
1- -
15.11.
Москва 5
1- -
Степанова
Чкалова18- 1- 18
1 .11.
Токио
5
41

42.

Недостатком экви-соединения является то, что
если соединение происходит по атрибутам с
одинаковыми наименованиями (а так чаще
всего и происходит), то в результирующем
отношении появляется два атрибута с
одинаковыми значениями.
Избавиться от этого недостатка можно, взяв
проекцию по всем атрибутам, кроме одного из
дублирующих.
Именно
так
действует
естественное
соединение.
42

43.

Операция
естественного
соединения применяется к двум
отношениям, имеющим общий
атрибут (простой или составной).
Этот атрибут в отношениях имеет
одно и то же имя и определён на
одном и том же домене.
43

44.

Результатом
операции
естественного
соединения является отношение R,
которое представляет собой проекцию
эквисоединения отношений R1 и R2 по
общему атрибуту на соединённую
совокупность
атрибутов
обоих
отношений.
Для естественного соединения используют
синтаксис
R1 JOIN R2
((R1 TIMES R2) WHERE f)[]
44

45.

Естественное соединение эквивалентно следующей
последовательности реляционных операций
1. Выполнить декартово произведение
отношений.
2. Выполнить выборку по совпадающим
значениям атрибутов, имеюшим
одинаковые имена.
3. Выполнить
проекцию,
удалив
повторяющиеся атрибуты.
45

46.

Можно
выполнять
последовательное
естественное
соединение
нескольких
отношений.
Естественное
соединение
обладает свойством ассоциативности, т.е.
поэтому такие соединения можно
записывать, опуская скобки:
A JOIN B JOIN C
46

47.

Дополнительные операции реляционной
алгебры (Дейт):
Переименование атрибута.
Расширение. Порождает новое отношение,
содержащее добавленный атрибут. Этот
атрибут рассчитывается по правилам,
задаваемым некоторым выражением.
Помимо обычных арифметических операций и
операций сравнения в выражении можно
использовать функции, называемые
итоговыми (Count,Sum,Avg,Max и т.д.).
Для изменения тела отношения
используются операции Insert, Delete,
Update.
47

48.

Номер поставщика Наименование поставщика
PNUM
1
PNAME
2
Петров
3
Сидоров
Иванов
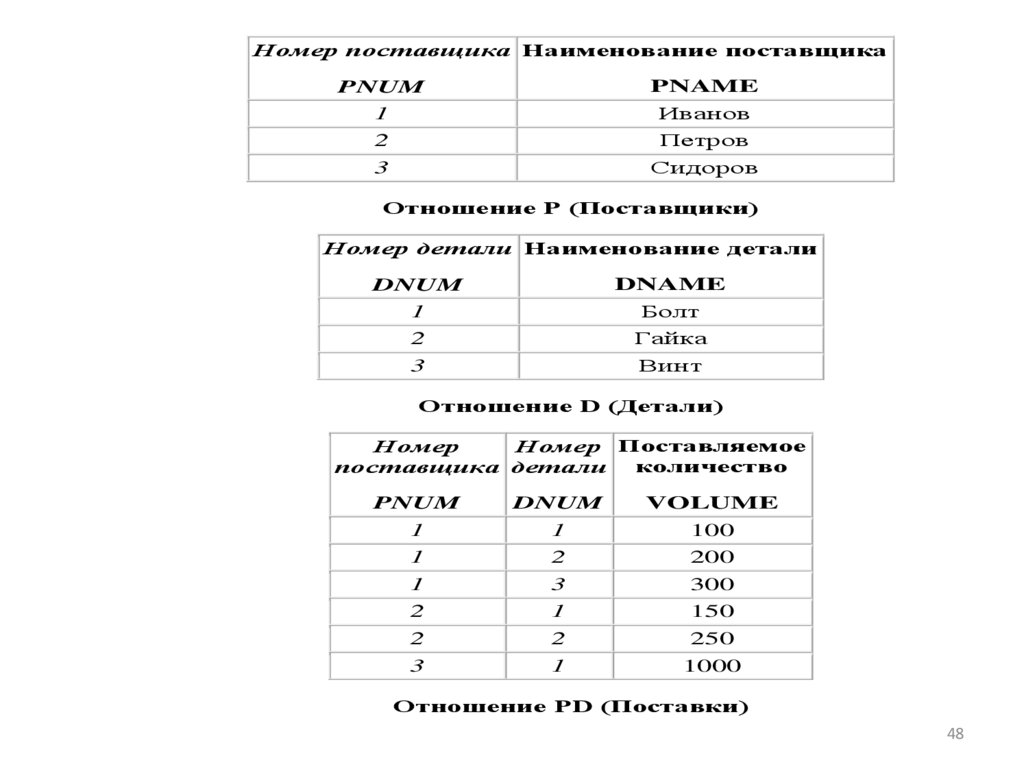
Отношение P (Поставщики)
Номер детали Наименование детали
DNUM
1
DNAME
2
Гайка
3
Винт
Болт
Отношение D (Детали)
Номер
Номер Поставляемое
количество
поставщика детали
PNUM
1
DNUM
1
VOLUME
1
2
200
1
3
300
2
1
150
2
2
250
3
1
1000
100
Отношение PD (Поставки)
48

49.

Пример 1. Получить имена
поставщиков, поставляющих
деталь номер 2.
49

50.

Пример 2. Получить имена поставщиков,
поставляющих по крайней мере одну
гайку.
50

51.

Пример 3. Получить имена поставщиков,
не поставляющих деталь номер 2.
51

52.

Языки исчислений, в отличие от реляционной
алгебры,
являются
непроцедурными
(описательными или декларативными) и
позволяют выражать запросы с помощью
предиката первого порядка (высказывания в
виде
функции),
которому
должны
удовлетворять
кортежи
или
домены
отношений.
Запрос к БД, выполненный с использованием
подобного
языка,
содержит
лишь
информацию о желаемом результате.
К языкам этой группы относится SQL.
52