Алгоритмы поиска кратчайших путей в графе

1.

Алгоритмы поиска кратчайших путей в графе
Автор: ученик 10А Рожок Алексей Дмитриевич
Руководитель: учитель информатики Петов Олег Владимирович

2.

Актуальность
Сейчас эта тема как никогда актуальна. Каждый хоть раз пользовался онлайн
картами, в которых реализованы данные алгоритмы. Поэтому эта тема так важна
в наши дни, когда много людей по всему миру путешествуют и используют
карты.
В жизни встречается довольно большое количество задач, которые могут быть
переформулированы в указанном виде — например, задача определения
времени поездки в метро (и оптимального маршрута). Google использует
алгоритм Дейкстры для сортировки важности страниц в выдаче. Также
алгоритмы поиска кратчайшего пути используются для поиска наикратчайших
путей в навигаторах и онлайн картах.

3.

Цель и задачи
Цель - Исследовать существующие алгоритмы поиска кратчайших путей.
Задачи индивидуального проекта для достижения цели:
1) Изучить самые известные алгоритмы для поиска кратчайших путей.
2) Описать работу алгоритмов.
3) Обосновать верность алгоритмов.

4.

5.

Алгоритм Форда-Беллмана
Алгоритм носит имя двух американских
учёных: Ричарда Беллмана (Richard Bellman) и
Лестера Форда (Lester Ford). Форд фактически
изобрёл этот алгоритм в 1956 г. при изучении другой
математической задачи, подзадача которой свелась к
поиску кратчайшего пути в графе, и Форд дал
набросок решающего эту задачу алгоритма. Беллман
в 1958 г. опубликовал статью, посвящённую
конкретно задаче нахождения кратчайшего пути, и в
этой статье он чётко сформулировал алгоритм в том
виде, в котором он известен нам сейчас.

6.

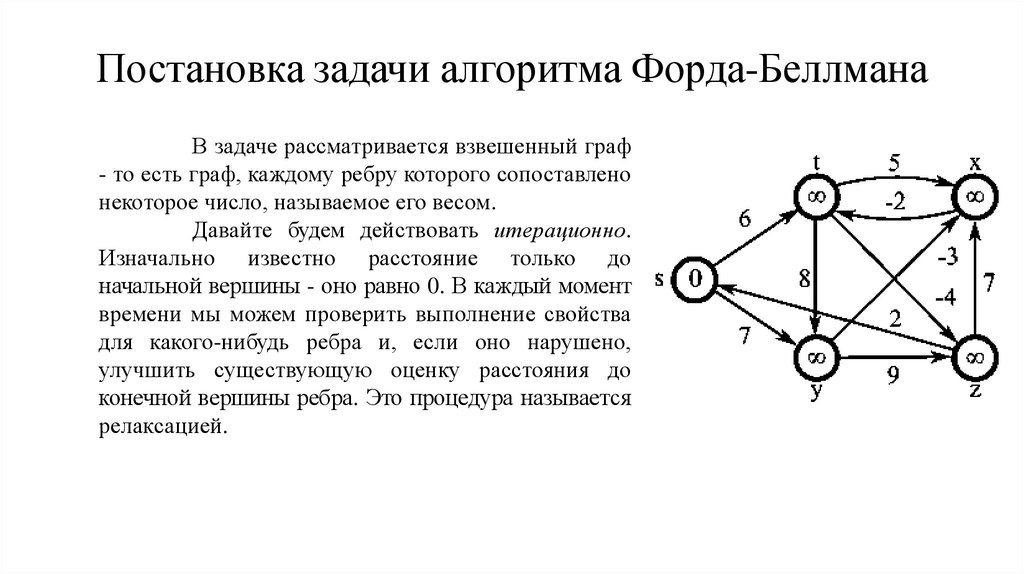
Постановка задачи алгоритма Форда-Беллмана
В задаче рассматривается взвешенный граф
- то есть граф, каждому ребру которого сопоставлено
некоторое число, называемое его весом.
Давайте будем действовать итерационно.
Изначально известно расстояние только до
начальной вершины - оно равно 0. В каждый момент
времени мы можем проверить выполнение свойства
для какого-нибудь ребра и, если оно нарушено,
улучшить существующую оценку расстояния до
конечной вершины ребра. Это процедура называется
релаксацией.