Основы логики

1. Основы логики

2. ЛОГИКА– это наука о формах и способах мышления

АЛГЕБРА ЛОГИКИ – раздел
математической логики,
изучающий высказывания и
операции над ними.

3. ПОНЯТИЕ – это форма мышления, фиксирующая основные, существенные признаки объекта.

Понятие имеет две стороны: содержание и
объем.
Содержание - это совокупность признаков
объекта.
Объем – это совокупность (количество)
объектов на которые эти признаки
распространяются.

4. Персоналии.

• Дж.Буль - автор извест-ных
произведений, в т.ч. работы
«Математический анализ
логики»(1847г.)
• Основной труд Дж. Буля «Исследование законов
мысли», в котором
представлен раздел логики алгебра высказываний.
Джордж Буль
1815 – 1864 г.г.

5. Основные понятия

Константы алгебры логики (булевой
алгебры) – логический 0 (ложь) и
логическая 1 (истина).
Логические переменные принимают
только два значения - логический 0 или
логическая 1.

6. Логической функцией F от набора логических переменных х1,х2,…,хn называется функция, которая может принимать только два

значения:
логический 0 или логическая 1.
Любая логическая функция может быть
задана с помощью таблицы истинности.

7. Основные логические операции:

• Конъюнкция, логическое умножение (and - И). Может
обозначаться как: ∧, &, *;
• Дизъюнкция, логическое сложение (or - или). Может
обозначатся как: ∨, ǀǀ, +;
• Инверсия, логическое отрицание (not - не). Может
обозначатся как: ¬ или знаком
над любой буквой (А);
• Импликация (
- следование)(если высказывание истинно,
то…)
• Эквивалентность (~ - тогда и только тогда, когда)
Высказывания в алгебре логики обозначаются латинскими
буквами

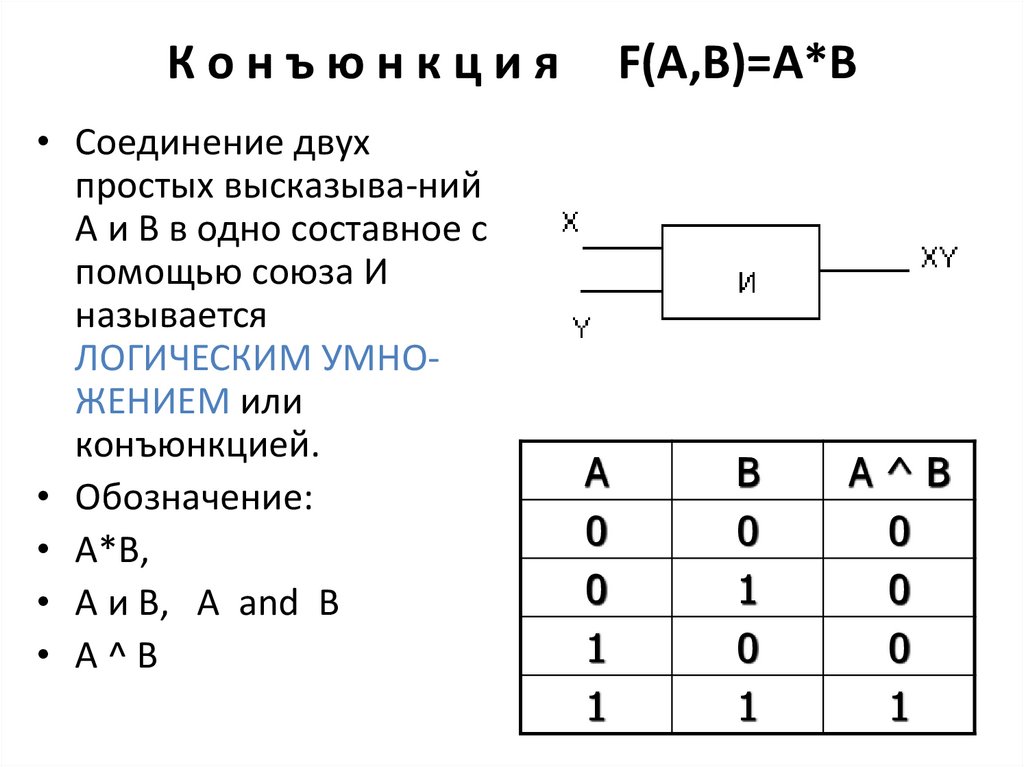
8. К о н ъ ю н к ц и я F(A,B)=A*B

Конъюнкция
• Соединение двух
простых высказыва-ний
А и В в одно составное с
помощью союза И
называется
ЛОГИЧЕСКИМ УМНОЖЕНИЕМ или
конъюнкцией.
• Обозначение:
• А*В,
• А и В, А and В
• А^В
F(A,B)=A*B
А
0
0
1
1
В
0
1
0
1
А^В
0
0
0
1

9. Д и з ъ ю н к ц и я F(A,B)=A ˇ B

Дизъюнкция
F(A,B)=A ˇ B
• Соединение двух простых
высказываний А и В в одно с
помощью союза ИЛИ,
употребляемого в
неисключающем смысле,
называется ЛОГИЧЕСКИМ
СЛОЖЕНИЕМ или
дизъюнкцией.
А
0
0
1
1
В
0
1
0
1
А или В
0
1
1
1
• Обозначение:
• А+В,
• А или В, А or В
• АˇВ

10. И н в е р с и я F(A)= не A

Инверсия
• Присоединение
частицы НЕ к
сказуемому данного
простого высказывания А называется
логическим
отрицанием.
• Обозначение:
не А
F(A)= не A
А
не А
0
1
1
0

11.

В
следующих
высказываниях
выделите
простые
высказывания, обозначив каждое из них буквой. Запишите с
помощью букв и знаков логических операций каждое
составное высказывание.
1) Число 376 чётное и трёхзначное.
2) Зимой дети катаются на коньках или на лыжах.
3) Новый год мы встретим на даче или на Красной площади.
4) Неверно, что Солнце движется вокруг Земли.
5) На уроке математики старшеклассники отвечали на
вопросы учителя, а также писали самостоятельную работу.

12. Теоремы алгебры логики

1. не 0 = 1, не 1 = 0
2. Х + 0=Х, Х · 1=Х
3. Х + 1=1, Х · 0=0
А+А+А+А=А
А·А·А=А

13. Теоремы алгебры логики

5. Х + не Х=1, Х · не Х=0
6. Не (не Х) = Х – закон двойного
отрицания
7. Х + Y = Y + X, X · Y = Y · X
коммутативный закон

14. Алгоритмы решения логических задач:

Большинство логических задач решается по
следующему алгоритму:
• изучение условия задачи
• обозначение используемых высказываний
буквами
• составление логических выражений,
удовлетворяющих всем требованиям задачи
• объединение их в одно выражение
• Вычисление всех значений этого логического
выражения
• проверка полученного решения по условию
задачи

15. СТАРШИНСТВО ЛОГИЧЕСКИХ ОПЕРАЦИЙ :

1. Инверсия
2. конъюнкция
3. дизъюнкция
4. сложение по модулю 2
Для изменения порядка действий
используются скобки.

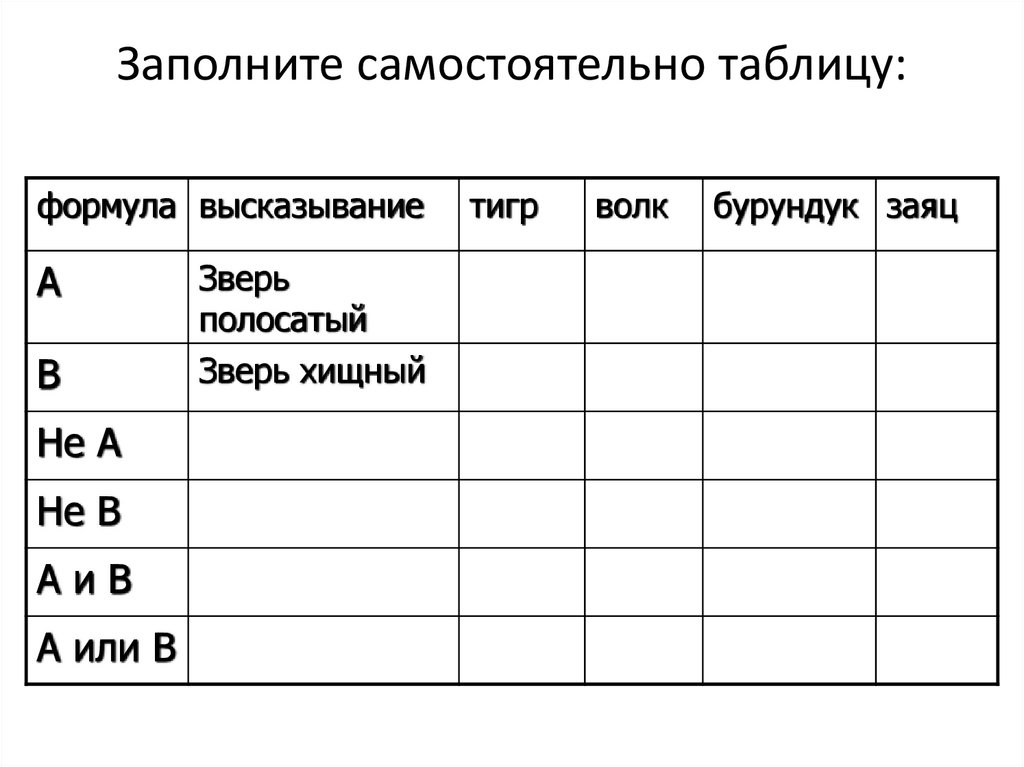
16. Заполните самостоятельно таблицу:

формула высказывание
А
В
Не А
Не В
АиВ
А или В
Зверь
полосатый
Зверь хищный
тигр
волк
бурундук заяц

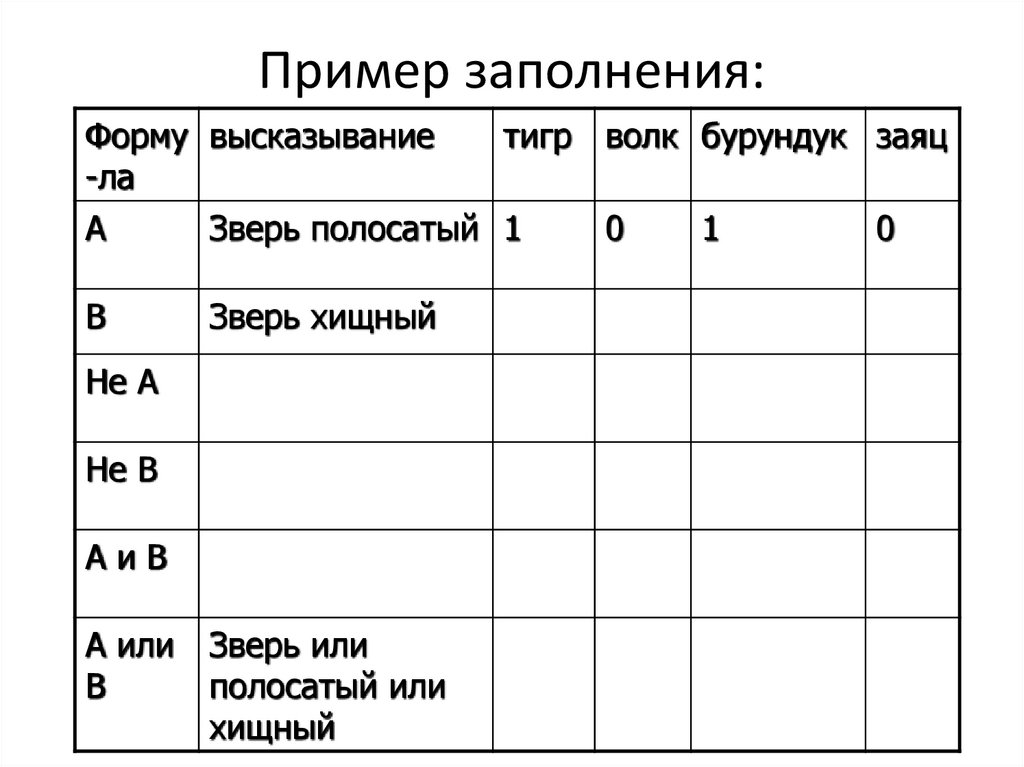
17. Пример заполнения:

Форму высказывание
тигр волк бурундук заяц
-ла
А
Зверь полосатый 1
0
1
0
В
Зверь хищный
Не А
Не В
АиВ
А или
В
Зверь или
полосатый или
хищный

18.

Задание
Даны два простых высказывания:
А = {2 * 2 = 4},
В = {2 * 2 = 5}.
Какие из высказываний истинны:
а) А;
б) В;
в) A ^ В;
г) A v B ;
д) ¬A;
ж) А ^ ¬В