Похожие презентации:
Решение задач с помощью систем линейных уравнений
1.
Решение задач с помощьюсистем линейных уравнений
2.
Способы решения систем линейныхуравнений:
• графический способ;
• способ подстановки;
• способ сложения.
3.
Задача. В корзине лежат бананы и яблоки. Известно, чтобананов на 5 больше, чем яблок. Сколько бананов и
сколько яблок в корзине, если всего в ней 17 фруктов?
Решение.
Пусть х – количество бананов в корзине, у – количество яблок.
х − у = 5,
ቊ
х + у = 17,
( х + х) + (– у + у) = 5 + 17,
х + х – у + у = 5 + 17,
2х = 22,
х = 11.
Ответ: 11 бананов и 6 яблок.
11 + у = 17,
у = 17 – 11,
у = 6.
4.
Чтобы решить задачу с помощьюсистемы уравнений, надо:
• выделить две неизвестные величины и обозначить их буквами;
• используя условие задачи, составить систему уравнений;
• решить систему уравнений удобным способом;
• истолковать результат в соответствии с условием задачи.
5.
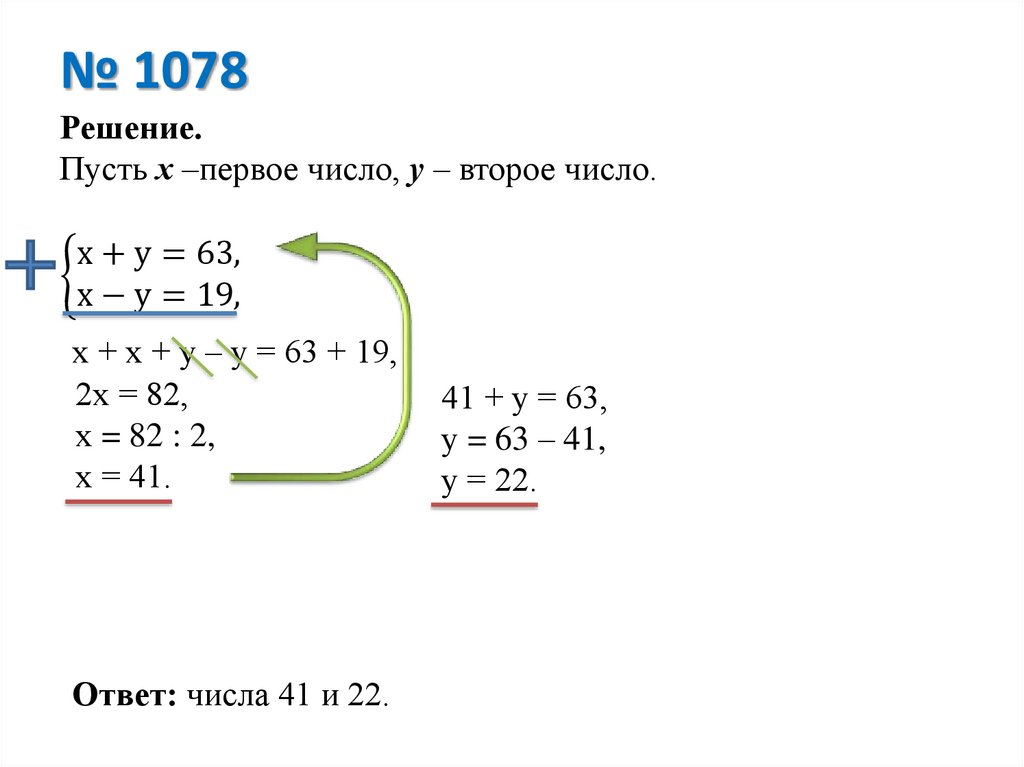
№ 1078Решение.
Пусть х –первое число, у – второе число.
х + у = 63,
ቊ
х − у = 19,
х + х + у – у = 63 + 19,
2х = 82,
х = 82 : 2,
х = 41.
Ответ: числа 41 и 22.
41 + у = 63,
у = 63 – 41,
у = 22.
6.
№1080. Купец купил 138 аршин черного и синего сукна за 540 р.Спрашивается, сколько аршин он купил того и другого, если синее
стоило 5 р. за аршин, а черное 3р.?
Решение.
Пусть х аршин черного сукна, у аршин синего сукна купил купец.
х + у = 138, ∙ (– 3)
ቊ
3х + 5у = 540,
−3х − 3у = −414,
ቊ
3х + 5у = 540,
– 3у + 5у = – 414 + 540,
2у = 126,
у = 126 : 2,
у = 63.
черное
синее
Всего
Количе
ство
х
у
138
Стоимо
сть
3х
5у
540
х + 63 = 138,
х = 138 – 63,
х = 75.
Ответ: 75 аршин черного сукна, 63 аршин синего.
7.
№1082. Чтобы накормить 4 лошадей и 12 коров, надо 120 кгсена в день, а чтобы накормить 3 лошадей и 20 коров – 167 кг
сена. Найдите дневную норму сена для лошади и для коровы.
Решение.
Пусть х кг травы съедает за день каждая лошадь, у кг съедает за
день каждая корова.
Лошади Коровы Всего/
4х + 12у = 120, ∙ 3
ቊ
3х + 20у = 167, ∙ (– 4)
12х + 36у = 360,
ቊ
−12х − 80у = −668,
36у – 80у = 360 – 668,
– 44у = –308,
у = –308 : (–44),
у = 7.
разница
I
4х
12у
120
II
3х
20у
167
3х + 20 ∙ 7 = 167,
3х +140 = 167,
3х = 167 – 140,
3х = 27,
х = 27 : 3,
х = 9.
Ответ: 9 кг съедает лошадь, 7 кг съедает корова.






 Математика
Математика








