Похожие презентации:
Метод средней точки
1.
ТЕМА: «МЕТОДСРЕДНЕЙ ТОЧКИ»
Выполнил: студент группы 3161
Сонин Н.П.
Преподаватель: доцент,
Потапов А.А.
2.
Целью данной работы является изучение метода средней точкиили метода Больцано.
Задача оптимизации заключается в нахождении оптимального
значения
некоторой
Оптимальное
функции
значение
может
при
заданных
быть
минимальным в зависимости от задачи.
ограничениях.
максимальным
или
3.
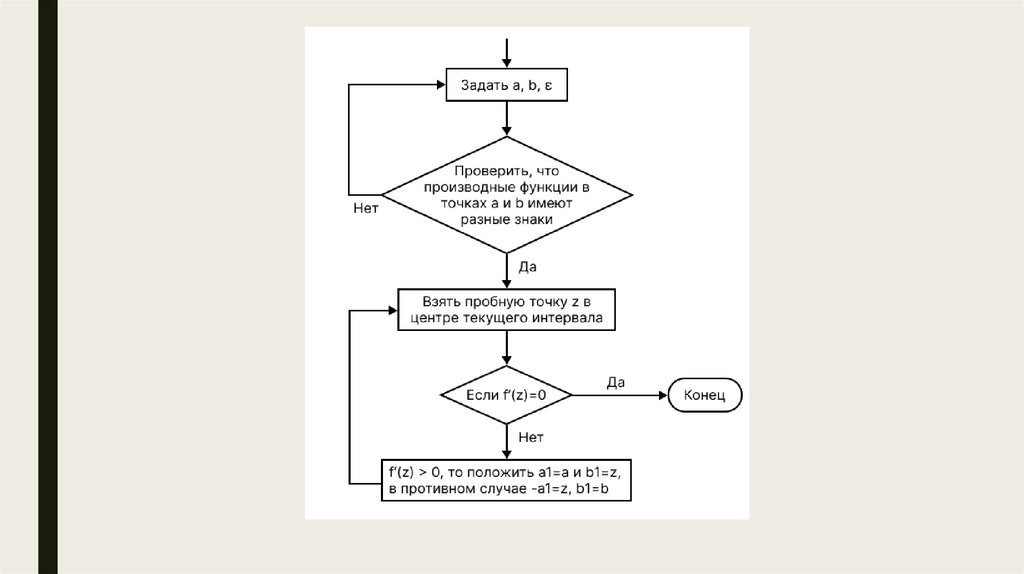
Суть метода заключается в следующем: на каждой итерацииметода выбирается середина отрезка, задаваемого начальными
границами, значения производных функции на концах которого
имеет различные знаки. Затем вычисляется значение производной
функции в этой точке. Если значение функции близко к нулю или
отрицательно, то новыми границами выбираются участки от начала
и до середины, и от середины до конца отрезка соответственно.
4.
5.
6.
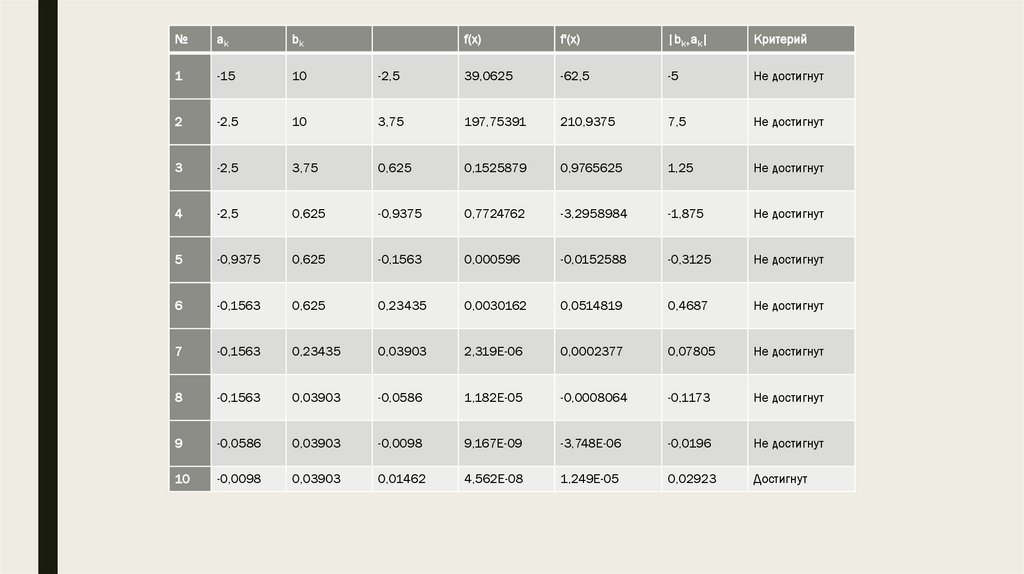
№ak
bk
f(x)
f'(x)
|bk+ak|
Критерий
1
-15
10
-2,5
39,0625
-62,5
-5
Не достигнут
2
-2,5
10
3,75
197,75391
210,9375
7,5
Не достигнут
3
-2,5
3,75
0,625
0,1525879
0,9765625
1,25
Не достигнут
4
-2,5
0,625
-0,9375
0,7724762
-3,2958984
-1,875
Не достигнут
5
-0,9375
0,625
-0,1563
0,000596
-0,0152588
-0,3125
Не достигнут
6
-0,1563
0,625
0,23435
0,0030162
0,0514819
0,4687
Не достигнут
7
-0,1563
0,23435
0,03903
2,319E-06
0,0002377
0,07805
Не достигнут
8
-0,1563
0,03903
-0,0586
1,182E-05
-0,0008064
-0,1173
Не достигнут
9
-0,0586
0,03903
-0,0098
9,167E-09
-3,748E-06
-0,0196
Не достигнут
10
-0,0098
0,03903
0,01462
4,562E-08
1,249E-05
0,02923
Достигнут
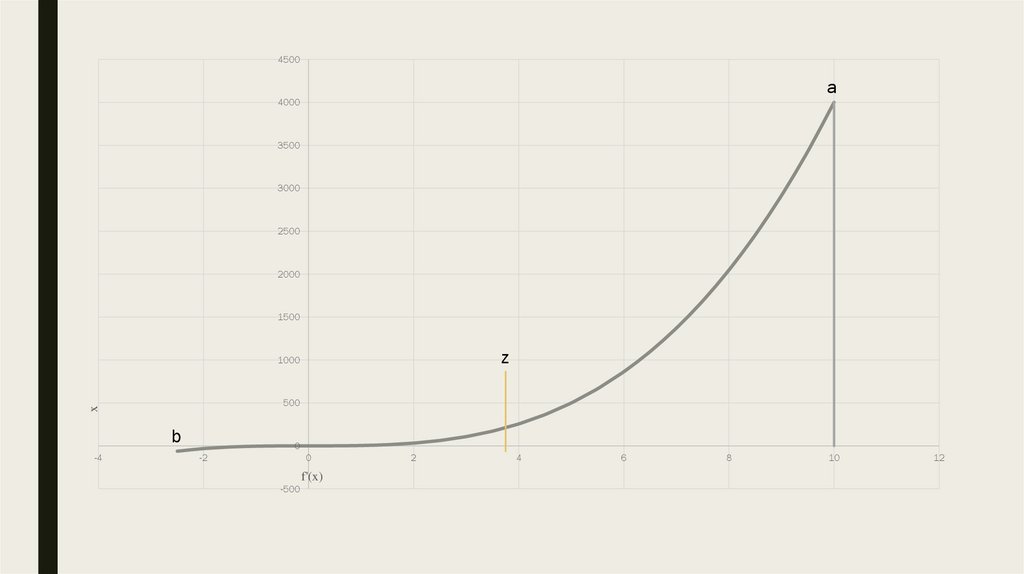
7.
60004000
x
2000
b
-20
-15
0
-10
-5
0
-2000
z
-4000
-6000
-8000
-10000
-12000
-14000
f'(x)
-16000
5
10
a
15
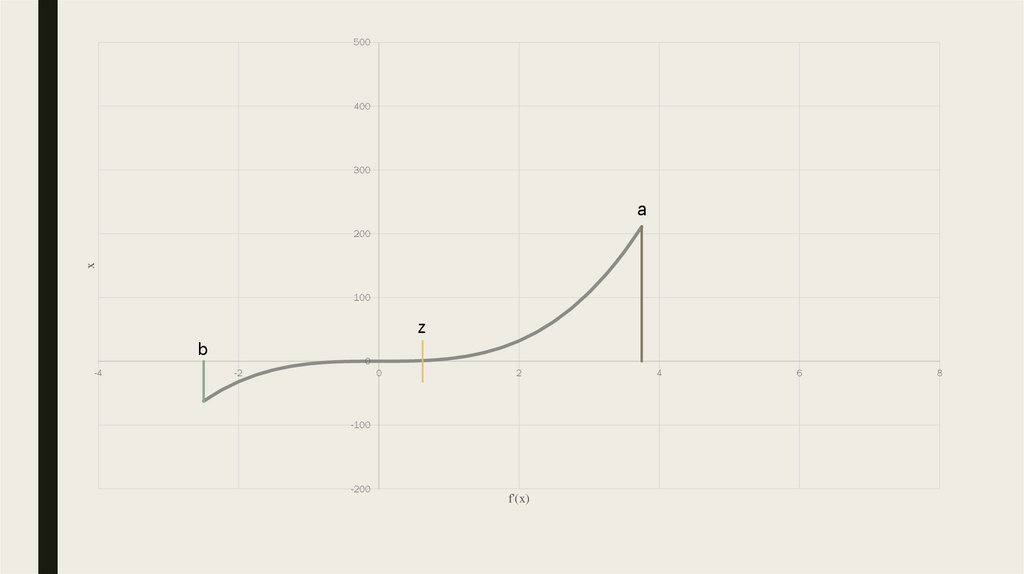
8.
4500a
4000
3500
3000
2500
2000
1500
z
1000
x
500
b
-4
0
-2
0
f'(x)
-500
2
4
6
8
10
12
9.
500400
300
a
x
200
100
z
b
-4
0
-2
0
2
-100
-200
f'(x)
4
6
8
10.
ВыводыВ данной работе рассмотрен метод средней точки. По
результатам работы можно сделать выводы, что метод средней
точки, как правило, позволяет существенно уменьшить время
поиска минимума функции.







 Математика
Математика








