Методы вычислений

1. Методы вычислений

1
Методы вычислений
1.
2.
3.
4.
5.
6.
Алгоритм Евклида
Решение уравнений
Оптимизация
Восстановление зависимостей
Статистика
Моделирование
© К.Ю. Поляков, 2009-2012

2. Методы вычислений

2
Методы вычислений
Тема 1. Алгоритм Евклида
© К.Ю. Поляков, 2009-2012

3.

Вычисление НОД
НОД = наибольший общий делитель двух
натуральных чисел – это наибольшее
число, на которое оба исходных числа
делятся без остатка.
Перебор:
1. Записать в переменную k минимальное из
двух чисел.
2. Если a и b без остатка делятся на k, то стоп.
3. Уменьшить k на 1.
это цикл с
4. Перейти к шагу 2.
условием!
?
?
Где будет НОД?
Почему алгоритм обязательно закончится?
3

4.

Вычисление НОД (перебор)
k := a; { или k := b; }
ИЛИ
while (a mod k <> 0) or
(b mod k <> 0) do
k := k - 1;
writeln ('НОД(', a, ',', b, ')=', k);
?
?
Почему можно начинать с любого числа?
Как начать с минимального?
много операций для больших чисел
4

5.

5
Алгоритм Евклида
НОД(a,b)= НОД(a-b, b)
= НОД(a, b-a)
Заменяем большее из двух чисел разностью
большего и меньшего до тех пор, пока они не
станут равны. Это и есть НОД.
Евклид
(365-300 до. н. э.)
Пример:
НОД (14, 21) = НОД (14, 21-14) = НОД (14, 7)
= НОД (7, 7) = 7

6.

Реализация алгоритма Евклида
пока a ≠ b делай
если a > b, то
a := a - b
иначе b := b - a;
?
Где будет НОД? Как его вывести?
много шагов при большой разнице чисел:
НОД (1998, 2) = НОД (1996, 2) = … = 2
6

7.

Модифицированный алгоритм Евклида
НОД(a,b)= НОД(a mod b, b)
= НОД(a, b mod a)
Заменяем большее из двух чисел остатком от деления
большего на меньшее до тех пор, пока меньшее не
станет равно нулю. Тогда большее — это НОД.
Пример:
НОД (14, 21) = НОД (14, 7) = НОД (0, 7) = 7
Еще один вариант:
НОД(2·a,2·b)= 2·НОД(a, b)
НОД(2·a,b)= НОД(a, b) // при нечетном b
7

8.

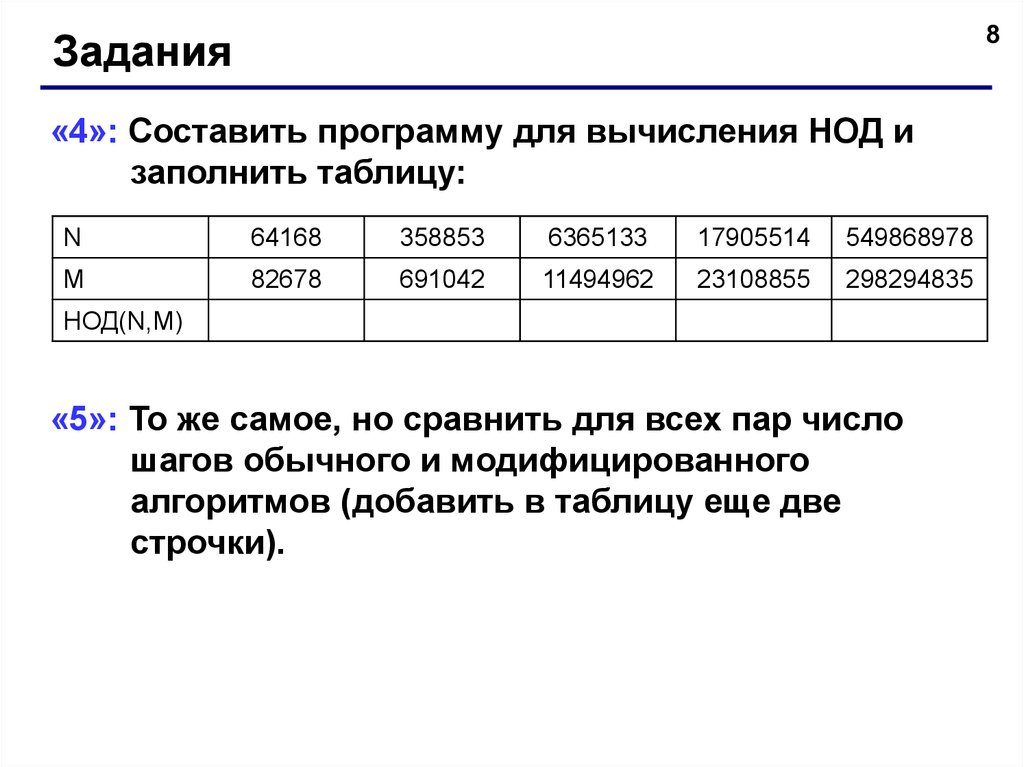
8
Задания
«4»: Составить программу для вычисления НОД и
заполнить таблицу:
N
64168
358853
6365133
17905514
549868978
M
82678
691042
11494962
23108855
298294835
НОД(N,M)
«5»: То же самое, но сравнить для всех пар число
шагов обычного и модифицированного
алгоритмов (добавить в таблицу еще две
строчки).

9. Методы вычислений

9
Методы вычислений
Тема 2. Решение уравнений
© К.Ю. Поляков, 2009-2012

10.

Методы решения уравнений
f (x) = 0
• Точные (аналитические)
sin x 0
x k , k Z
• Приближенные
y
• графические
x*
a
b
x
• численные
(методы последовательного приближения):
1)по графику найти интервал [a, b], в котором находится
x* (или одно начальное приближение x0)
2)по некоторому алгоритму уточнить решение, сужая
интервал, в котором находится x*
3)повторять шаг 2, пока не достигнута требуемая
точность:
b–a<
10

11.

11
Численные методы
Применение: используются тогда, когда точное
(аналитическое) решение неизвестно или очень
трудоемко.
• дают хотя бы какое-то решение
• во многих случаях можно оценить ошибку и найти
решение с заданной точностью
• решение всегда приближенное, неточное
x 1 4 sin( x 1) 0
x 1,3974
x 1,3974

12.

12
Метод прямого перебора
Задача: найти решение уравнения f (x) = 0 на интервале
[a, b] с заданной точностью (чтобы найденное
решение отличалось от истинного не более, чем на ).
y
x*
a
b
x
Алгоритм:
a* b*
• разбить интервал [a, b] на полосы шириной
• найти полосу [a*, b*], в которой находится x*
• решение – a* или b*
?
Как улучшить решение?

13.

13
Есть ли решение на [a, b]?
есть решение
y
y
нет решения
x*
a
нет решения
x*
bx
a b
a b
x
x*
f (a) 0
f (a) 0
f (a) 0
f (b) 0
f (b) 0
f (b) 0
f (a) f (b) 0
!
y
f (a ) f (b) 0
Если непрерывная функция f (x) имеет разные
знаки на концах интервала [a, b], то в некоторой
точке x внутри [a, b] она равна 0, то есть f (x) = 0!
x

14.

14
Метод прямого перебора
eps := 0.001; { точность решения }
x := a;
пока f(x)*f(x+eps) > 0 делай
x := x + eps; { к следующему интервалу}
конец
ответ := x;
Как повысить точность
без лишних вычислений?
?
eps := 0.001; { точность решения }
x := a;
while f(x)*f(x+eps) > 0 do begin
x := x + eps; { к следующему интервалу}
end;
x := x + eps/2;
Что опасно?
?

15.

Метод прямого перебора
program qq;
var ...: real;
function f(x: real): real;
begin
f := -x;
end;
begin
{ основная программа }
end.
?
Как найти все решения на [a,b]?
15

16.

16
Задания
«4»: Найти все решения уравнения x 5 cos( x 1)
на интервале [-5,5] и вывести их на экран.
2
«5»: Сделать то же самое с помощью только одного
цикла.

17.

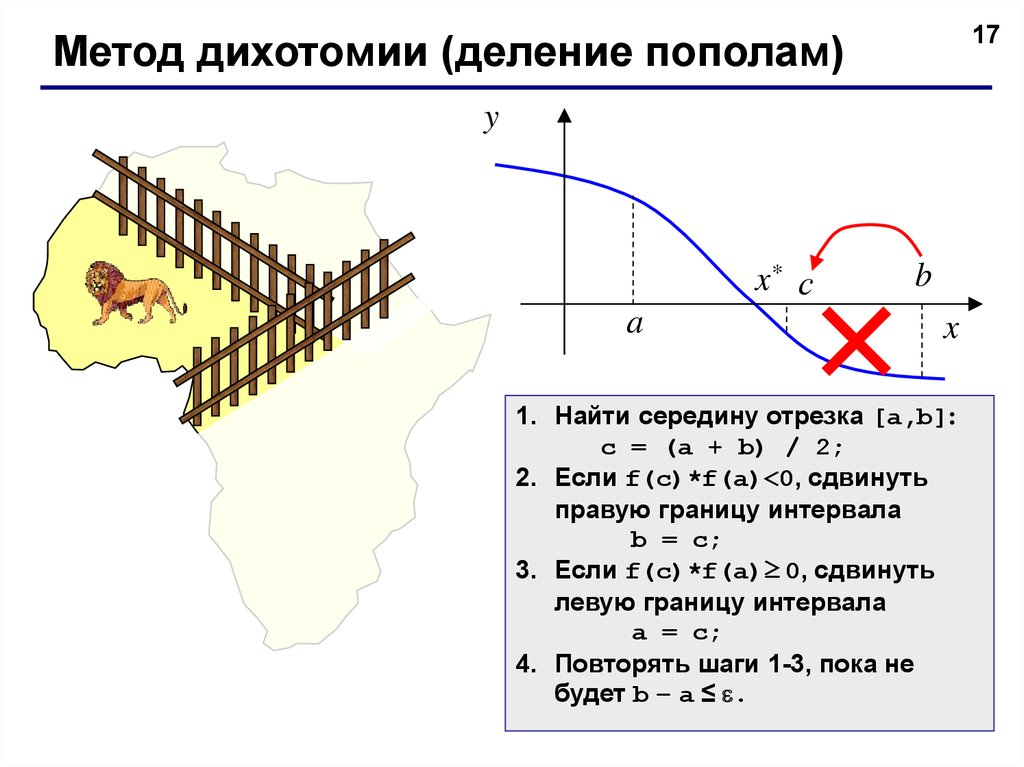
17
Метод дихотомии (деление пополам)
y
x* с
a
b
x
1. Найти середину отрезка [a,b]:
c = (a + b) / 2;
2. Если f(c)*f(a)<0, сдвинуть
правую границу интервала
b = c;
3. Если f(c)*f(a)≥ 0, сдвинуть
левую границу интервала
a = c;
4. Повторять шаги 1-3, пока не
будет b – a ≤ .

18.

Метод дихотомии (деления пополам)
• простота
• можно получить решение с любой заданной
точностью
• нужно знать интервал [a, b]
• на интервале [a, b] должно быть только одно
решение
• большое число шагов для достижения высокой
точности
• только для функций одной переменной
18

19.

Метод дихотомии (в программе)
пока b - a > eps
c := (a + b) /
если f(a)*f(c)
b := c
иначе a := c;
конец
ответ := (a + b)
делай
2;
< 0 то
/ 2;
19

20.

20
Задания
«4»: Найти все решения уравнения x 5 cos( x 1)
на интервале [-5,5] методом дихотомии и
вывести их на экран.
2
«5»: Сделать задачу на «4» и сравнить число шагов
цикла при использовании метода перебора и
метода дихотомии.

21.

Решение уравнений в Exсel
21
Задача: найти все решения уравнения x 2 5 cos x
на интервале [-5,5]
?
Как решить математическими методами?
Методы решения уравнений:
• аналитические: решение в виде формулы x ...
• численные: приближенное решение, число
1) выбрать начальное приближение x0 «рядом» с
решением
?
Как выбрать начальное приближение?
2) по некоторому алгоритму вычисляют первое
приближение, затем – второе и т.д. x0 x1 x2 ...
3) вычисления прекращают, когда значение меняется очень
*
мало (метод сходится) x0 ... x15 x16 x

22.

Решение уравнения x 5 cos x
22
2
1. Таблица значений функций на интервале [-5,5]
2. Графики функций (диаграмма «Точечная»)
2 решения:
начальные приближения
x0 1,5
x0 1,5

23.

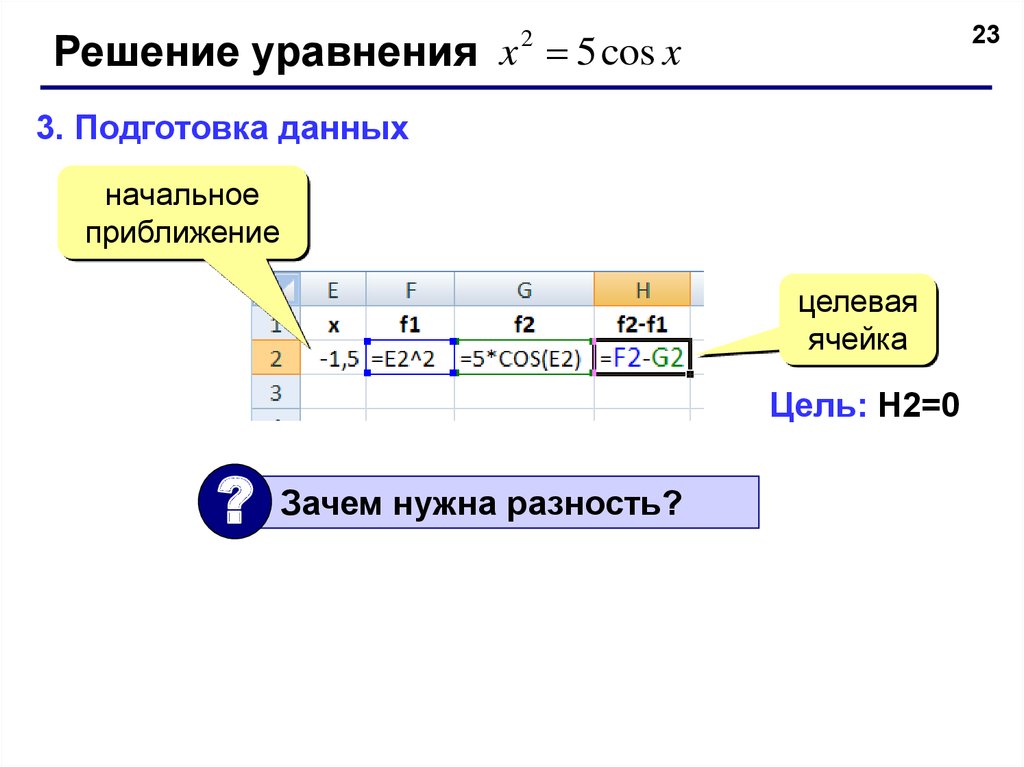
Решение уравнения x 5 cos x
23
2
3. Подготовка данных
начальное
приближение
целевая
ячейка
Цель: H2=0
?
Зачем нужна разность?

24.

Решение уравнения x 5 cos x
24
2
4. Подбор параметра
ошибка
решение
уравнения
?
?
Как найти второе решение?
Почему
не нуль?

25.

25
Плавающее бревно
На сколько погрузится бревно радиуса R, брошенное в
воду, если плотность дерева ρд = 700 кг/м3. Плотность
воды ρв = 1000 кг/м3?
L
H

26.

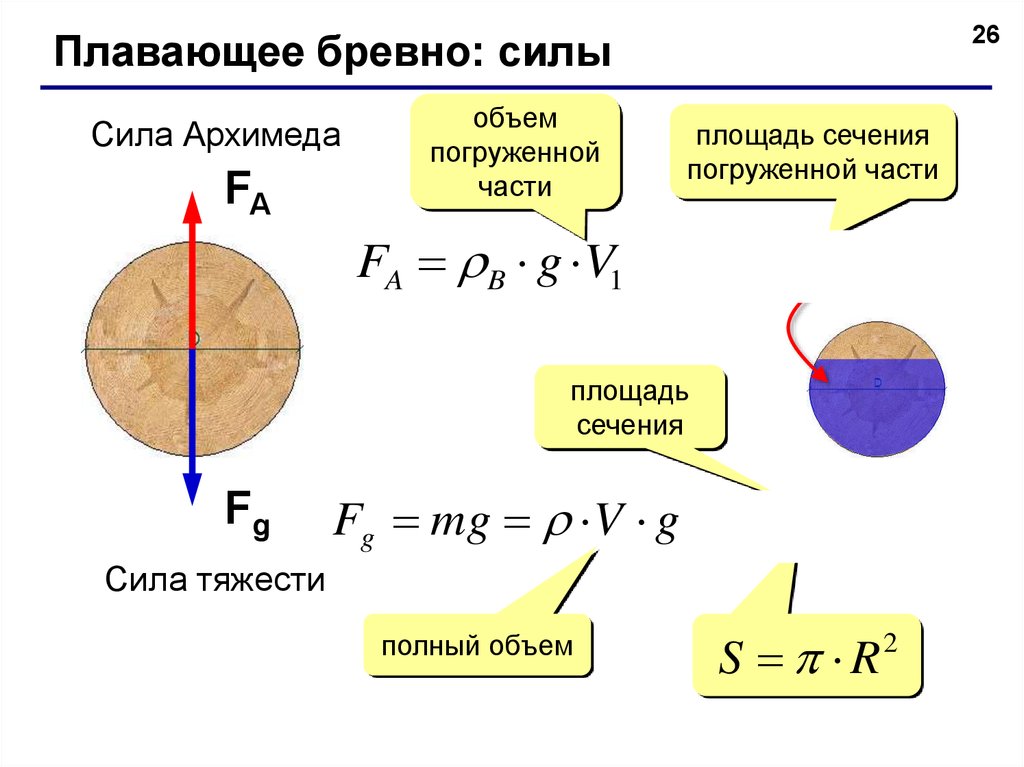
26
Плавающее бревно: силы
Сила Архимеда
FA
объем
погруженной
части
площадь сечения
погруженной части
FA B g V1 B g S1 L
площадь
сечения
Fg
Fg mg V g S L g
Сила тяжести
полный объем
S R
2

27.

Плавающее бревно: равновесие
Сила Архимеда
FA
FA Fg
B S1 L g S L g
B S1 S
Fg
Сила тяжести
неизвестно
27

28.

28
Плавающее бревно: площадь сечения
S1
R
1 2
S0 R
2
2 sin
/2
R
2
cos
2
sin
1
S 2 R sin R cos
2
2
2
1 2
S R sin
2
1 2
S1 R S 0 S R R ( sin )
2
2
2

29.

29
Плавающее бревно: уравнение
B S1 S
1 2
2
2
B R R ( sin ) R
2
найти α
/2
R
H
R
H R R cos
2

30. Методы вычислений

30
Методы вычислений
Тема 3. Оптимизация
© К.Ю. Поляков, 2009-2012

31.

31
Оптимизация
Оптимизация – это поиск оптимального (наилучшего)
варианта в заданных условиях.
Оптимальное решение – такое, при котором некоторая
заданная функция (целевая функция) достигает
минимума или максимума.
Постановка задачи:
• целевая функция
(расходы, потери, ошибки)
f ( x) min
f ( x) max
(доходы, приобретения)
• ограничения, которые делают задачу осмысленной
Задача без ограничений: построить дом
при минимальных затратах.
Решение: не строить дом вообще.

32.

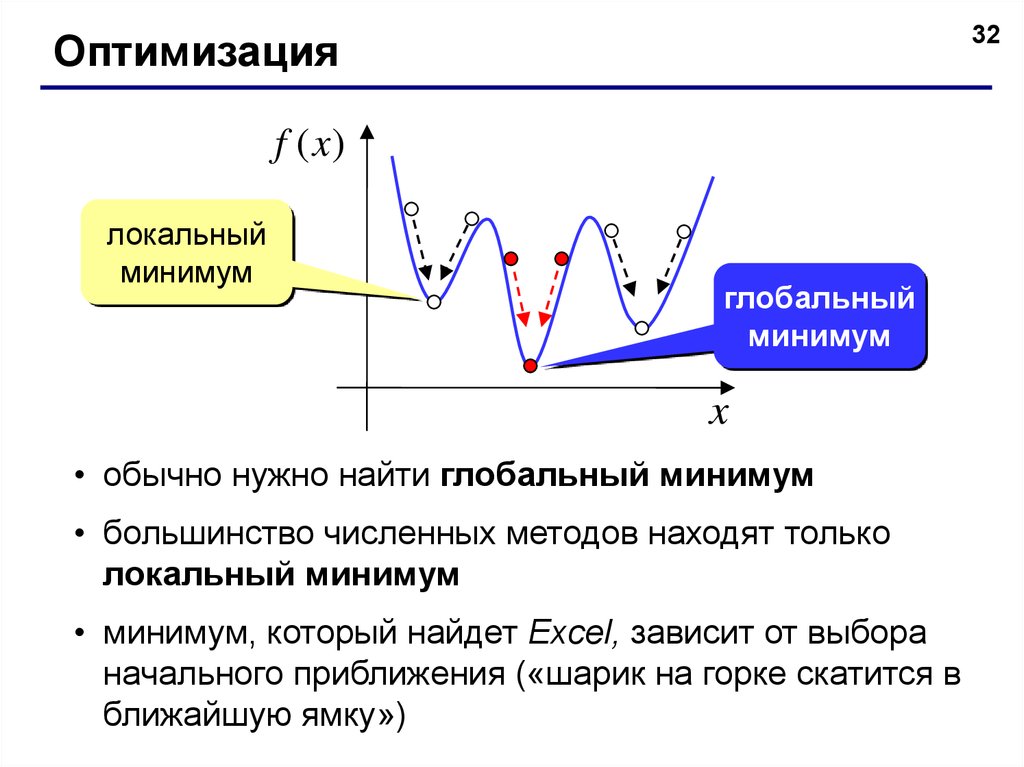
32
Оптимизация
f (x)
локальный
минимум
глобальный
минимум
x
• обычно нужно найти глобальный минимум
• большинство численных методов находят только
локальный минимум
• минимум, который найдет Excel, зависит от выбора
начального приближения («шарик на горке скатится в
ближайшую ямку»)

33.

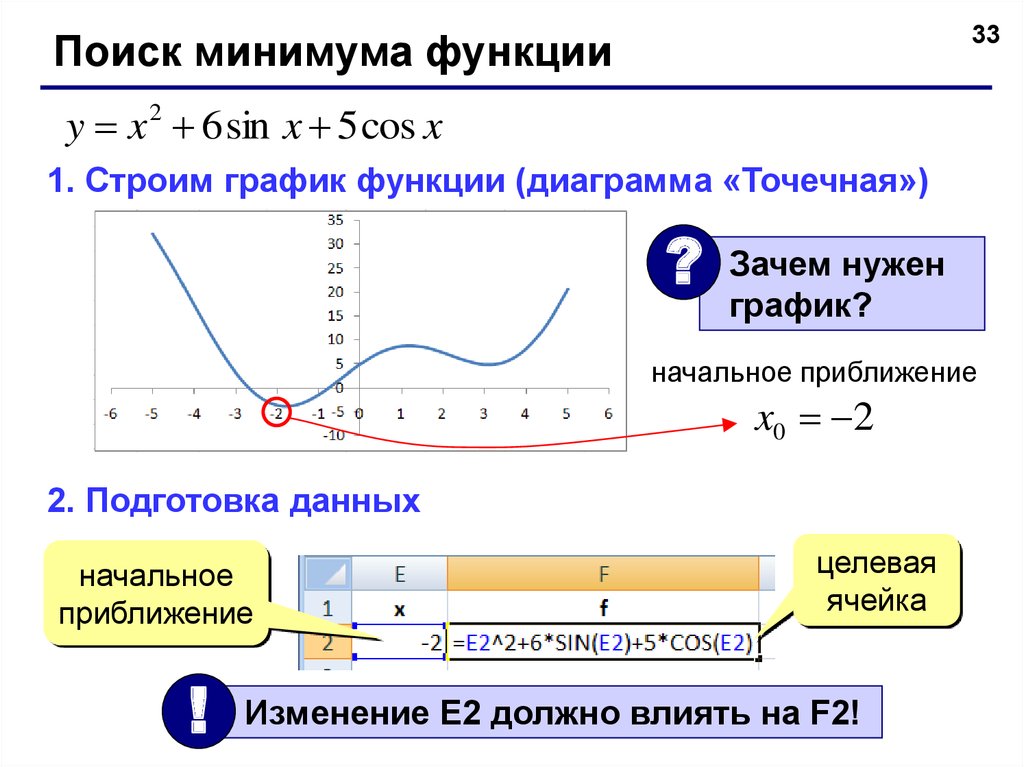
33
Поиск минимума функции
y x 2 6 sin x 5 cos x
1. Строим график функции (диаграмма «Точечная»)
?
Зачем нужен
график?
начальное приближение
x0 2
2. Подготовка данных
начальное
приближение
!
целевая
ячейка
Изменение E2 должно влиять на F2!

34.

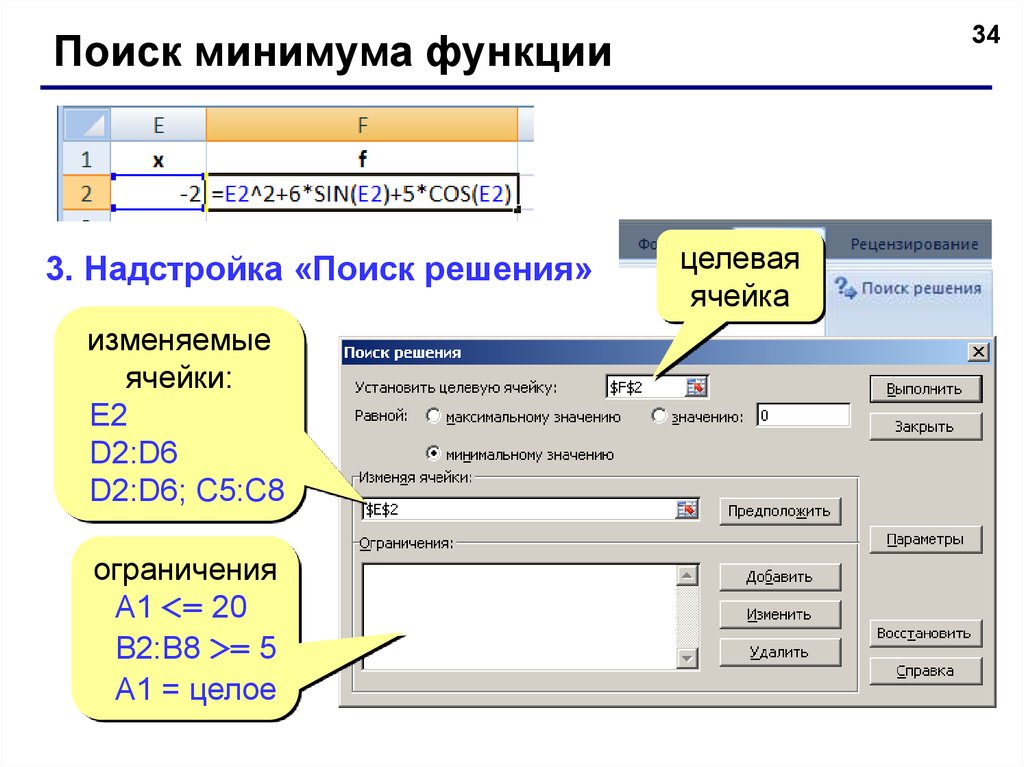
34
Поиск минимума функции
3. Надстройка «Поиск решения»
изменяемые
ячейки:
E2
D2:D6
D2:D6; C5:C8
ограничения
A1 <= 20
B2:B8 >= 5
A1 = целое
целевая
ячейка

35.

Параметры оптимизации
35

36.

Оптимизация
?
Подбор параметра – это оптимизация?
Надстройка «Поиск решения» позволяет:
• искать минимум и максимум функции
• использовать несколько изменяемых ячеек и
диапазонов
• вводить ограничения (<=, >=, целое, двоичное)
?
Как влияет ограничение «A1-целое» на
сложность решения задачи?
36

37. Методы вычислений

37
Методы вычислений
Тема 4. Восстановление
зависимостей
© К.Ю. Поляков, 2009-2012

38.

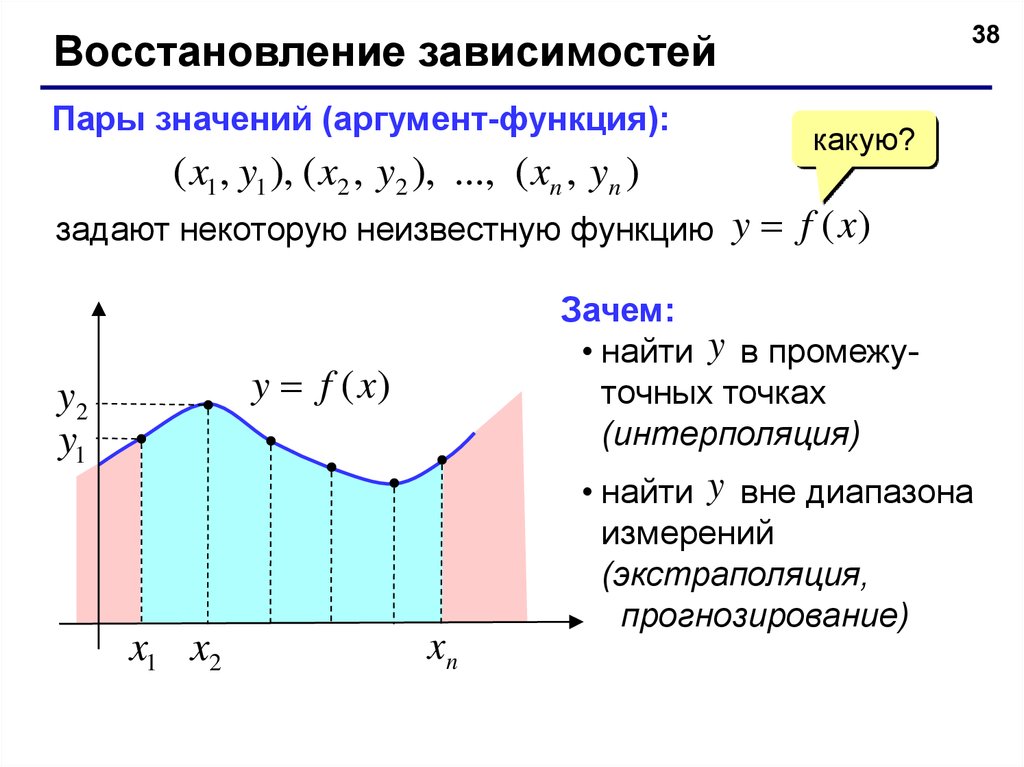
38
Восстановление зависимостей
Пары значений (аргумент-функция):
( x1 , y1 ), ( x2 , y2 ), ..., ( xn , yn )
какую?
задают некоторую неизвестную функцию y f (x)
Зачем:
• найти y в промежуточных точках
(интерполяция)
y f (x)
y2
y1
x1 x2
xn
• найти y вне диапазона
измерений
(экстраполяция,
прогнозирование)

39.

Какое решение нам нужно?
y f 2 ( x)
y f1 ( x)
y2
y1
x1 x2
!
xn
Через заданный набор точек проходит
бесконечно много разных кривых!
Вывод: задача некорректна, поскольку решение
неединственно.
39

40.

40
Восстановление зависимостей
Корректная задача: найти функцию заданного вида,
которая лучше всего соответствует данным.
Примеры:
y f (x)
• линейная y a x b
y2
• полиномиальная
y1
y a3 x 3 a2 x 2 a1 x a0
• степенная y a x
• экспоненциальная
b
x1 x2
!
xn
График функции не
обязательно проходит
через заданные точки!
y a ebx
• логарифмическая
y a ln x b
?
Как выбрать
функцию?

41.

Что значит «лучше всего соответствует»?
Метод наименьших квадратов (МНК):
y f (x)
y2
y1
( xi , yi ) заданные пары
значений
Yi f ( xi )
Y1 Y2
n
( yi Yi ) 2 min
i 1
x1 x2
?
xn
Зачем возведение в квадрат?
1) чтобы складывать положительные значения
2) решение сводится к системе линейных
уравнений (просто решать!)
41

42.

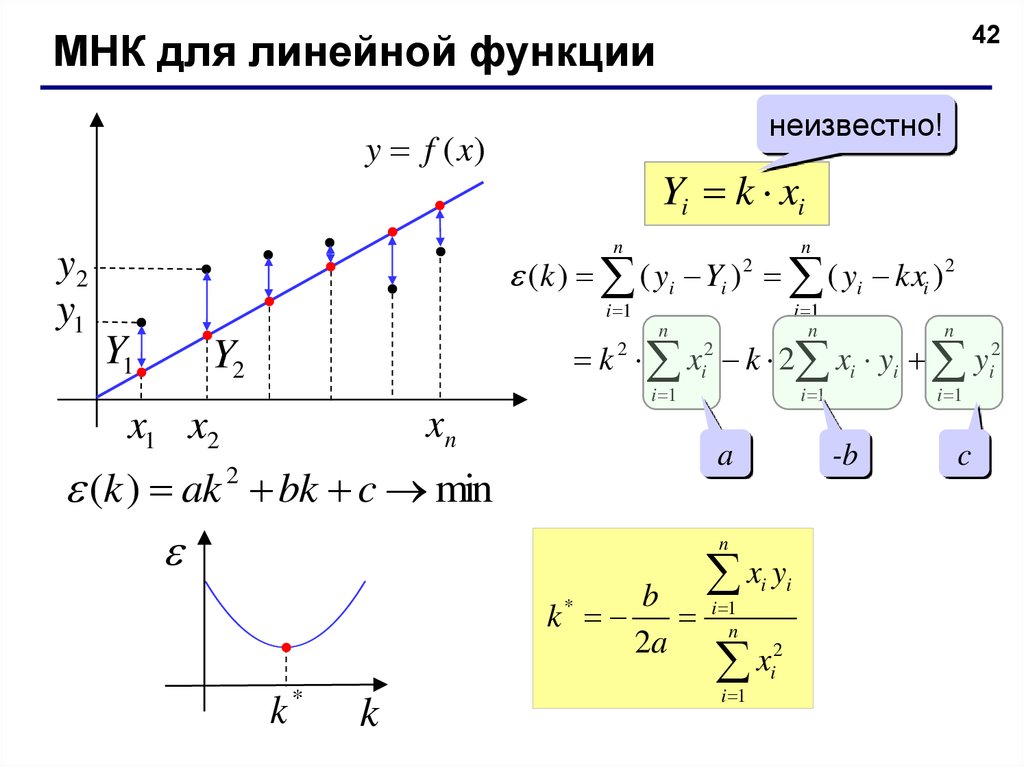
42
МНК для линейной функции
неизвестно!
y f (x)
y2
y1
Yi k xi
n
n
(k ) ( yi Yi ) ( yi kxi ) 2
2
i 1
Y1
i 1
n
n
n
k x k 2 xi yi yi2
Y2
2
i 1
xn
x1 x2
(k ) ak bk c min
k
x y
i 1
n
i
2
x
i
i 1
i 1
-b
n
b
*
k
2a
k
i 1
a
2
*
2
i
i
c

43.

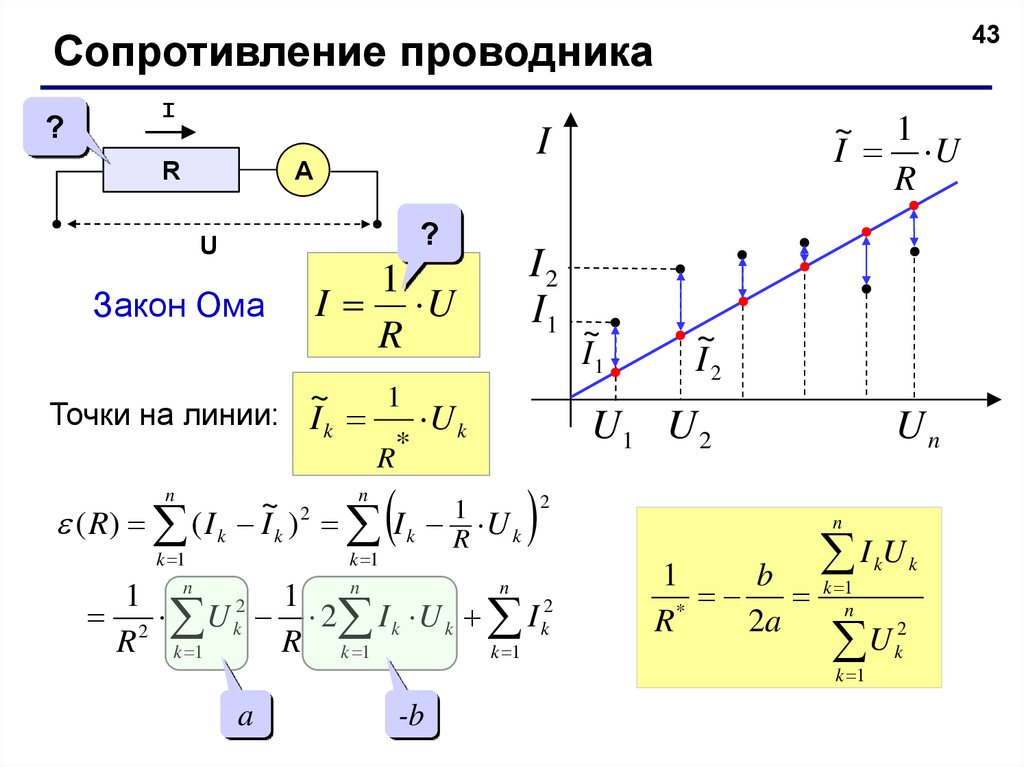
43
Сопротивление проводника
?
I
R
A
?
U
Закон Ома
1
I U
R
~
Точки на линии: I k
1
*
R
n
k 1
n
I2
I1 ~
I1
U k
~ 2 n
( R) ( I k I k ) I k R1 U k
k 1
n
~ 1
I U
R
I
~
I2
U1 U 2
Un
2
n
1
1
2
2 U k 2 I k U k I k2
R k 1
R k 1
k 1
n
1
b
*
R
2a
I U
k 1
n
2
U
k
k 1
a
-b
k
k

44.

Обработка результатов эксперимента
Задача. В файле mnk.txt записаны в столбик 10 пар
чисел (напряжение, ток), полученные в результате
эксперимента с одним резистором. Найти (приближенно)
его сопротивление по методу наименьших квадратов.
n
1
*
R
I U
k 1
n
k
n
k
2
U
k
R*
2
U
k
k 1
n
I U
k 1
k 1
k
k
Этапы решения:
1.Прочитать данные из файла в массивы U и I.
n
n
2.Вычислить
3.Вычислить
I U
k 1
R*.
k
k
и
2
U
k.
k 1
44

45.

Переменная типа 45
«текстовый файл»:
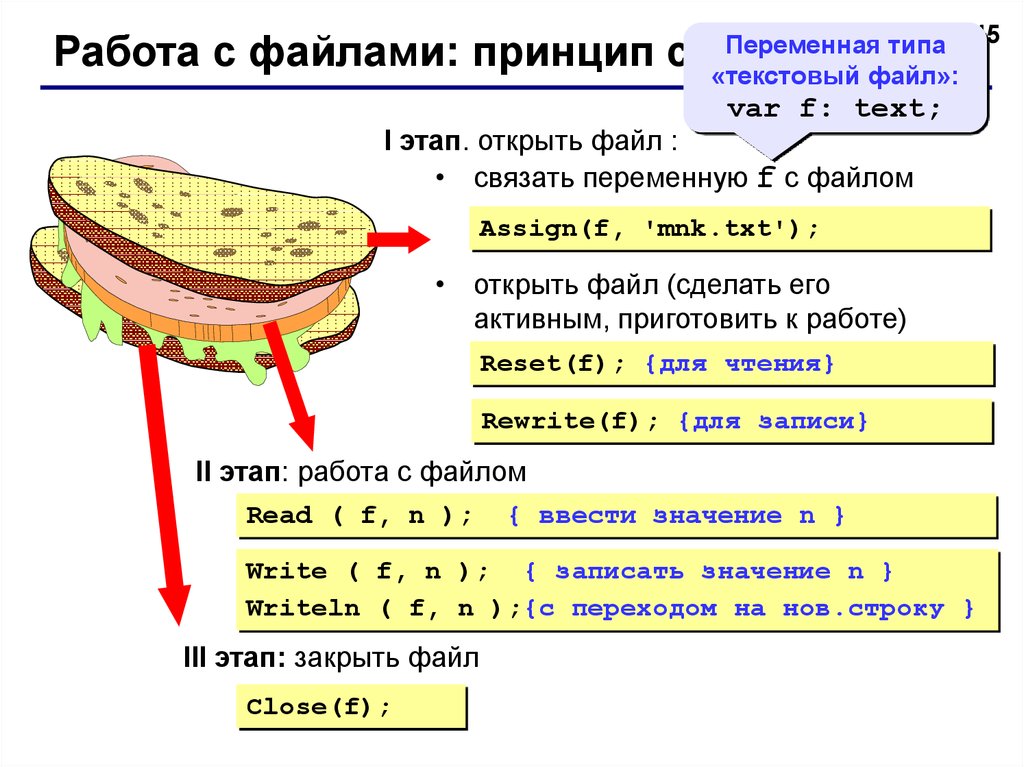
Работа с файлами: принцип сэндвича
var f: text;
I этап. открыть файл :
• связать переменную f с файлом
Assign(f, 'mnk.txt');
• открыть файл (сделать его
активным, приготовить к работе)
Reset(f); {для чтения}
Rewrite(f); {для записи}
II этап: работа с файлом
Read ( f, n );
{ ввести значение n }
Write ( f, n ); { записать значение n }
Writeln ( f, n );{c переходом на нов.строку }
III этап: закрыть файл
Close(f);

46.

Обработка результатов эксперимента
Чтение данных:
U, I: array[1..10] of real;
var f: text;
k: integer;
...
begin
Assign(f, 'mnk.txt');
Reset(f);
for k:=1 to 10 do begin
Read(f, U[k], I[k]);
Writeln(U[k]:0:3, ' ', I[k]:0:3);
end;
Close(f);
end.
?
Какие переменные и массивы
надо объявить?
46

47.

47
Обработка результатов эксперимента
Вычисления:
n
var UU: real;
2
U
k
...
k 1
UU := 0;
for k:=1 to 10 do begin
UU := UU + U[k]*U[k];
end;
?
?
n
Как найти
I kU k ?
k 1
?
Что вычисляем?
Как найти R*?
n
R*
2
U
k
k 1
n
I U
k 1
k
k

48.

48
Задания
«4»: Используя метод наименьших квадратов, найти
приближенное значение сопротивления по
данным файла mnk.txt.
«5»: Сделать то же самое, предполагая, что в файле
неизвестное количество пар значений, но не
более 100. Цикл ввода должен выглядеть так:
пока не достигнут конец
файла (eof = end of file)
while not eof(f) do begin
{ читаем U[k] и I[k] }
{ тут еще что-то надо сделать }
end;

49.

Коэффициент достоверности (Excel)
n
R 1
2
(y Y )
i 1
n
i
2
i
2
(
y
y
)
i
i 1
( xi , yi ) заданные пары
значений
Yi f ( xi )
y – среднее значение yi
Крайние случаи:
• если график проходит через точки:
R 1
2
• если считаем, что y не меняется и
R2 0
!
Yi y :
Фактически – метод наименьших квадратов!
49

50.

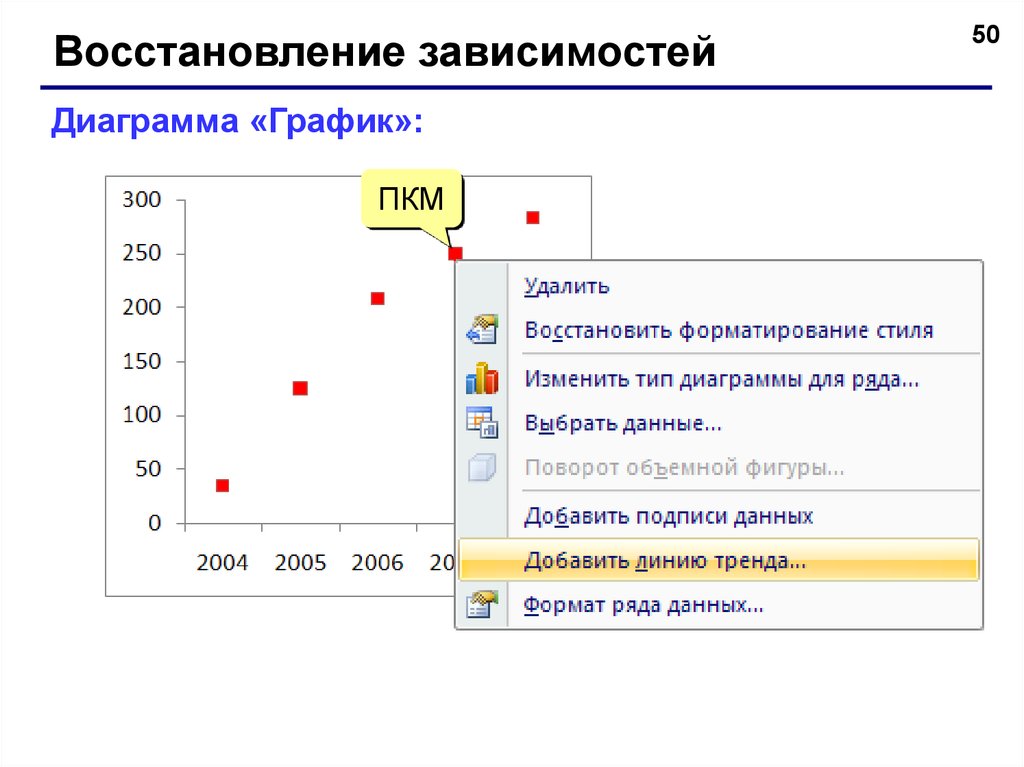
Восстановление зависимостей
Диаграмма «График»:
ПКМ
50

51.

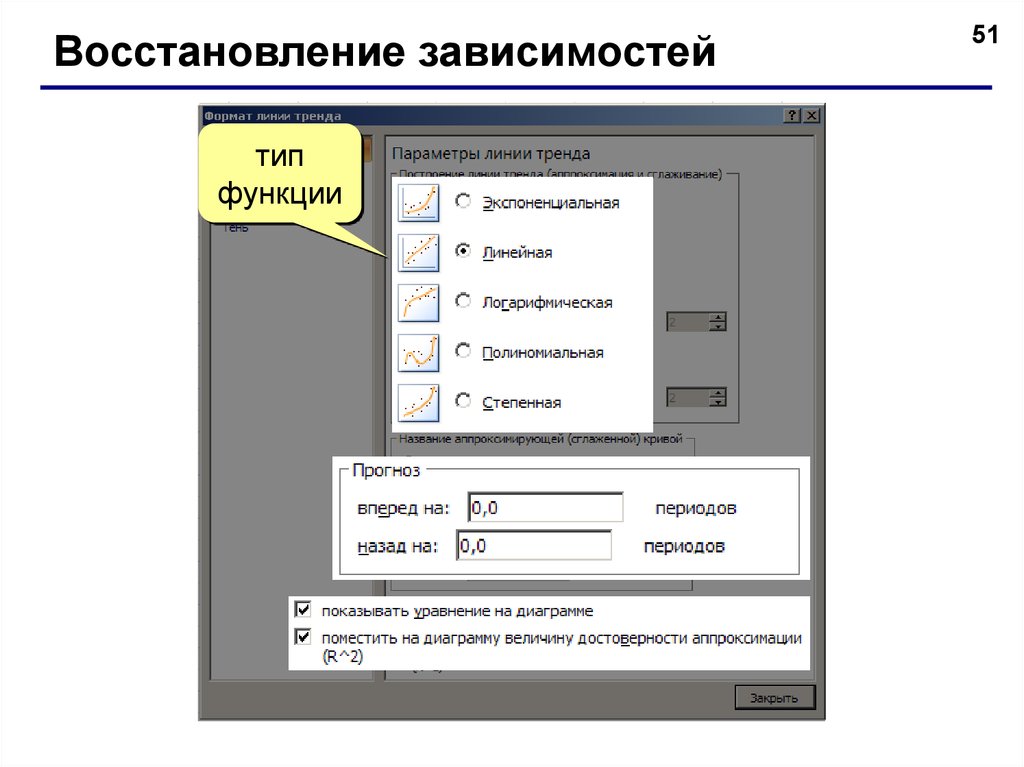
Восстановление зависимостей
тип
функции
51

52.

52
Восстановление зависимостей
?
!
?
Что такое
x?
В диаграмме «График»
x 1 для первой точки,
x 2 для второй и т.д.
Насколько хорошо выбрана функция?

53.

53
Восстановление зависимостей
Сложные случаи (нестандартная функция):
f ( x) a sin kx b
?
Что делать?
Алгоритм:
1) выделить ячейки для хранения a, k , b
2) построить ряд Yi f ( xi ) для тех же xi
3) построить на одной диаграмме ряды yi и Yi
4) попытаться подобрать a, k , b так, чтобы
два графика были близки
2
5) вычислить R в отдельной ячейке
функции: СУММКВРАЗН – сумма квадратов разностей рядов
ДИСПР – дисперсия
6) Поиск решения:
!
R min
2
Это задача оптимизации!

54. Методы вычислений

54
Методы вычислений
Тема 5. Статистика
© К.Ю. Поляков, 2009-2012

55.

Ряд данных и его свойства
55
Ряд данных – это упорядоченный набор значений
x1 , x2 , ..., xn
Основные свойства (ряд A1:A20):
• количество элементов =СЧЕТ(A1:A20)
• количество элементов, удовлетворяющих
некоторому условию:
= СЧЕТЕСЛИ(A1:A20;"<5")
• минимальное значение =МИН(A1:A20)
• максимальное значение =МАКС(A1:A20)
• сумма элементов =СУММ(A1:A20)
• среднее значение =СРЗНАЧ(A1:A20)

56.

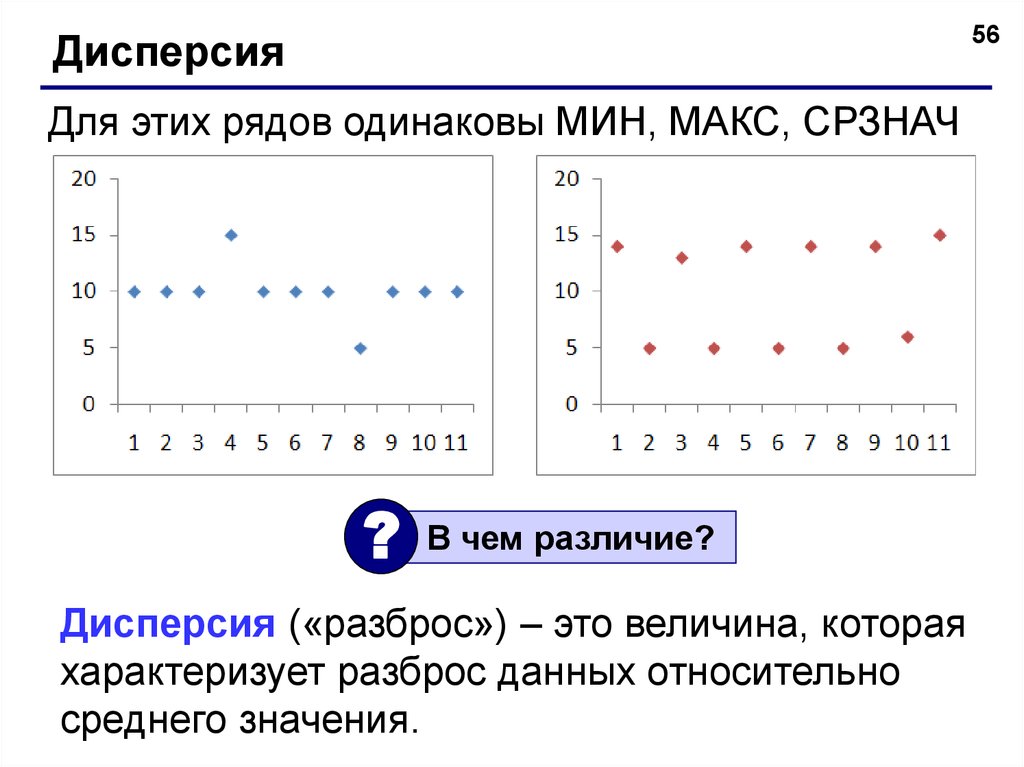
56
Дисперсия
Для этих рядов одинаковы МИН, МАКС, СРЗНАЧ
?
В чем различие?
Дисперсия («разброс») – это величина, которая
характеризует разброс данных относительно
среднего значения.

57.

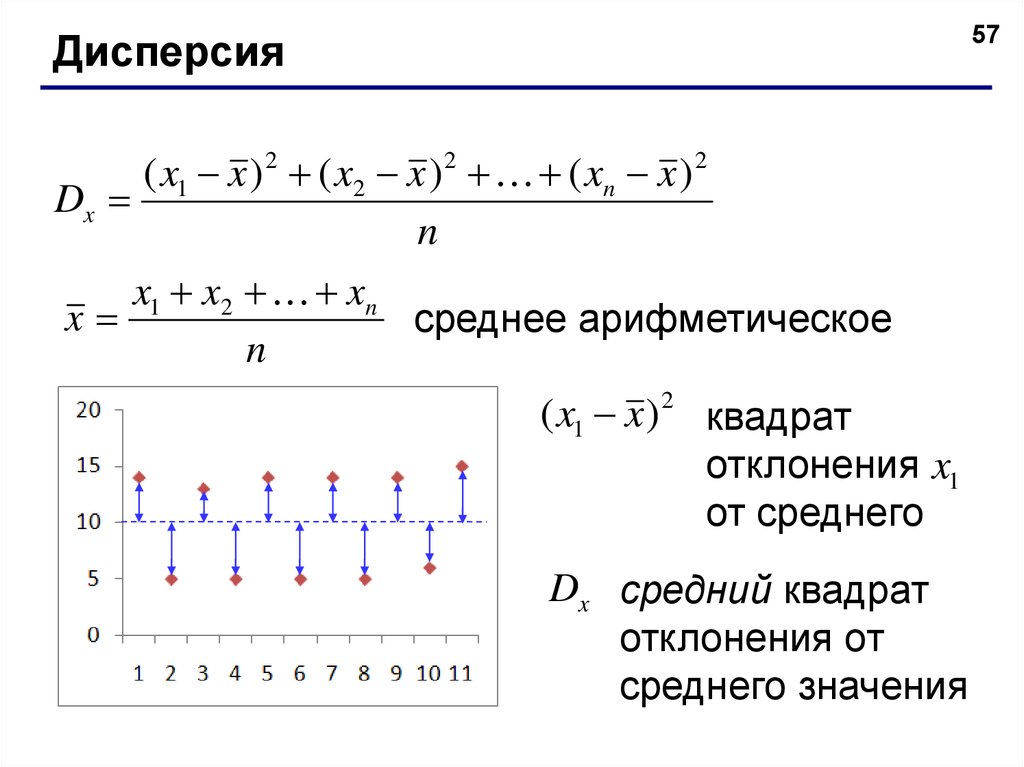
57
Дисперсия
n
2
(
x
x
)
i
( x1 x ) 2 ( x2 x ) 2 ( xn x ) 2 i 1
Dx
n
n
x1 x2 xn
x
среднее арифметическое
n
( x1 x )
2
квадрат
отклонения x1
от среднего
Dx средний квадрат
отклонения от
среднего значения

58.

58
Дисперсия и СКВО
Стандартная функция
=ДИСПР(A1:A20)
Функции – Другие – Статистические
Что неудобно:
если x измеряется в метрах,
то Dx – в м2
?
В каких
единицах
измеряется?
СКВО = среднеквадратическое отклонение
x Dx
=СТАНДОТКЛОНП(A1:A20)

59.

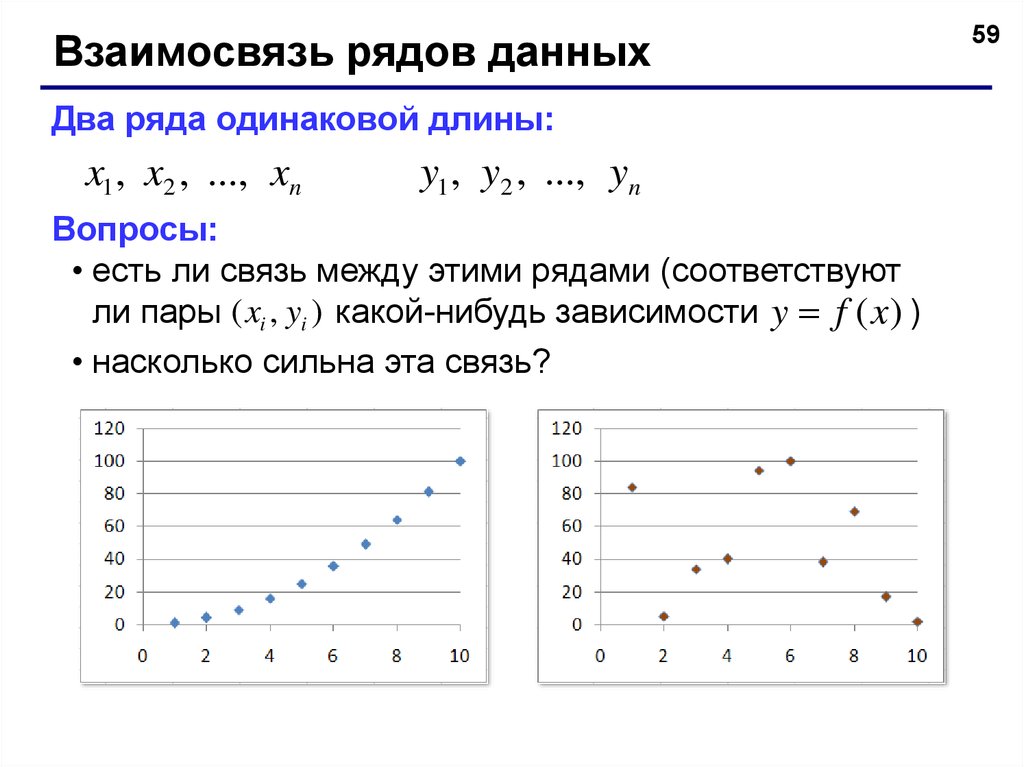
Взаимосвязь рядов данных
Два ряда одинаковой длины:
x1 , x2 , ..., xn
y1 , y2 , ..., yn
Вопросы:
• есть ли связь между этими рядами (соответствуют
ли пары ( xi , yi ) какой-нибудь зависимости y f (x) )
• насколько сильна эта связь?
59

60.

60
Взаимосвязь рядов данных
Ковариация:
n
K xy
?
Если x и
x
i 1
i
x y i y
n
y – один и тот же ряд?
K xx Dx
в среднем!
Как понимать это число?
• если K xy 0 увеличение x приводит к увеличению y
• если K xy 0 увеличение x приводит к уменьшению y
• если K xy 0 связь обнаружить не удалось
Что плохо?
• единицы измерения: если x в метрах, y в литрах,
то K xy – в м л
• K xy зависит от абсолютных значений x и y , поэтому
ничего не говорит о том, насколько сильна связь

61.

61
Взаимосвязь рядов данных
Коэффициент корреляции:
xy
?
K xy
x y
x, y
Какова размерность?
– СКВО рядов
x
и
y
безразмерный!
1 xy 1
Как понимать это число?
• если xy 0 : увеличение x приводит к увеличению y
• если xy 0 : увеличение x приводит к уменьшению y
• если xy 0 : связь обнаружить не удалось
=КОРРЕЛ(A1:A20;B1:B20)

62.

Взаимосвязь рядов данных
62
Как понимать коэффициент корреляции?
0 xy 0,2 : очень слабая корреляция
0,2 xy 0,5 : слабая
0,5 xy 0,7 : средняя
0,7 xy 0,9 : сильная
0,9 xy 1 : очень сильная
xy 1 : линейная зависимость y ax b, a 0
xy 1 : линейная зависимость y ax b, a 0
?
Если xy 0 , то связи нет?
!
Метод для определения линейной зависимости!

63. Методы вычислений

63
Методы вычислений
Тема 6. Моделирование
(по мотивам учебника А.Г. Гейна и др., Информатика и ИКТ,
10 класс, М.: Просвещение, 2008)
© К.Ю. Поляков, 2009-2012

64.

64
Модель деления
N
i
N 0 – начальная численность
N 2 N0
N1 2N 0 – после 1 цикла деления
N 2 2 N1 4 N 0 – после 2-х циклов
i
N0
N i 2 N i 1 2 N 0
Особенности модели:
1) не учитывается смертность
2) не учитывается влияние внешней среды
3) не учитывается влияние других видов
i

65.

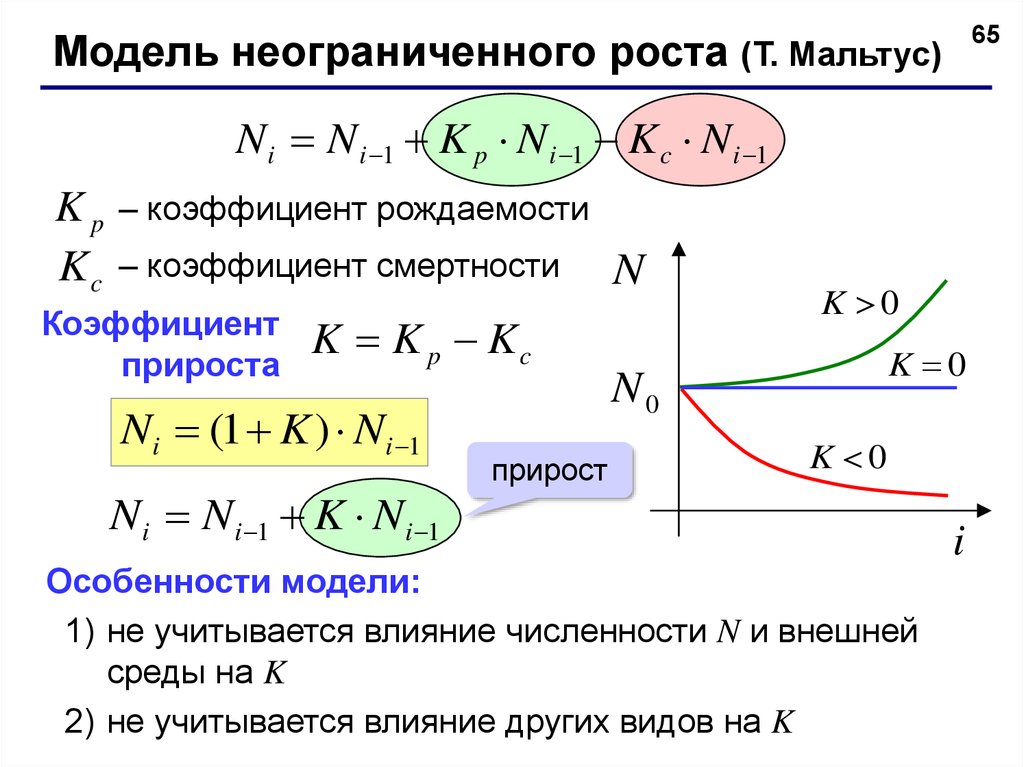
65
Модель неограниченного роста (T. Мальтус)
N i N i 1 K p N i 1 K c N i 1
Kp
Kc
– коэффициент рождаемости
– коэффициент смертности
Коэффициент
прироста
N
K K p Kc
Ni (1 K ) Ni 1
Ni Ni 1 K N i 1
K 0
K 0
N0
прирост
K 0
Особенности модели:
1) не учитывается влияние численности N и внешней
среды на K
2) не учитывается влияние других видов на K
i

66.

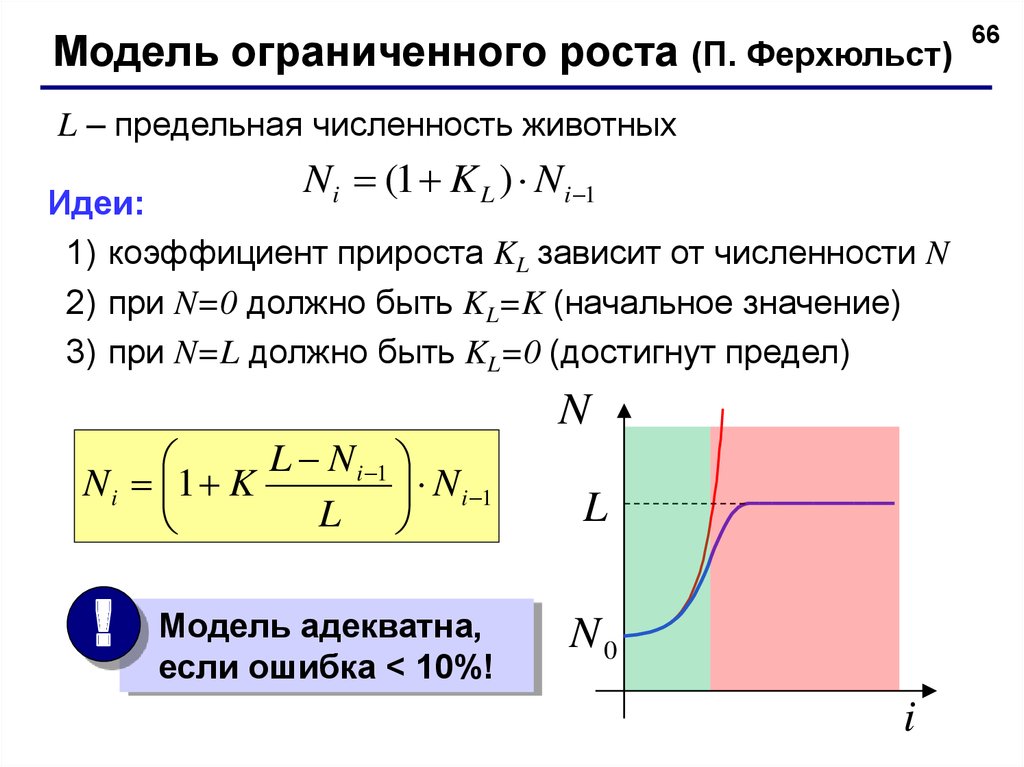
Модель ограниченного роста (П. Ферхюльст)
L – предельная численность животных
Ni (1 K L ) Ni 1
Идеи:
1) коэффициент прироста KL зависит от численности N
2) при N=0 должно быть KL=K (начальное значение)
3) при N=L должно быть KL=0 (достигнут предел)
L N i 1
N i 1 K
N i 1
L
!
Модель адекватна,
если ошибка < 10%!
N
L
N0
i
66

67.

67
Модель с отловом
Примеры: рыбоводческое хозяйство, разведение
пушных зверей и т.п.
L N i 1
N i 1 K
N i 1 R
L
?
отлов
Какая будет численность?
N i N i 1, прирост = отлову
L N
N N K
N R
L
?
K
N2 K N R 0
L
Сколько можно отловить?

68.

68
Модель эпидемии гриппа
L – всего жителей
Ni – больных в i-ый день
Zi – заболевших в i-ый день
Vi – выздоровевших
Wi – всего выздоровевших за i дней
Основное уравнение:
Ni Ni 1 Zi Vi
Ограниченный рост:
L N i 1 Wi 1
Zi K
N i 1 N i 1
L L
Выздоровление
(через 7 дней):
Vi Zi 7
Wi Wi 1 Vi
N
L
болели и
выздоровели
N0
i

69.

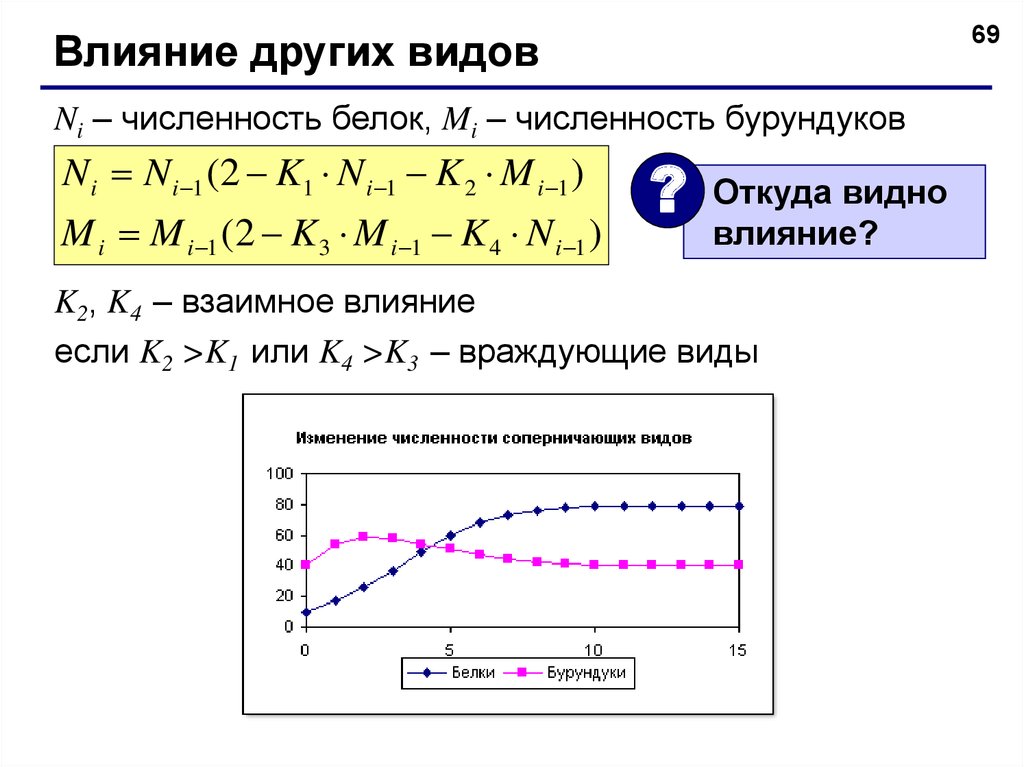
69
Влияние других видов
Ni – численность белок, Mi – численность бурундуков
N i N i 1 (2 K1 N i 1 K 2 M i 1 )
M i M i 1 (2 K 3 M i 1 K 4 N i 1 )
?
Откуда видно
влияние?
K2, K4 – взаимное влияние
если K2 >K1 или K4 >K3 – враждующие виды

70.

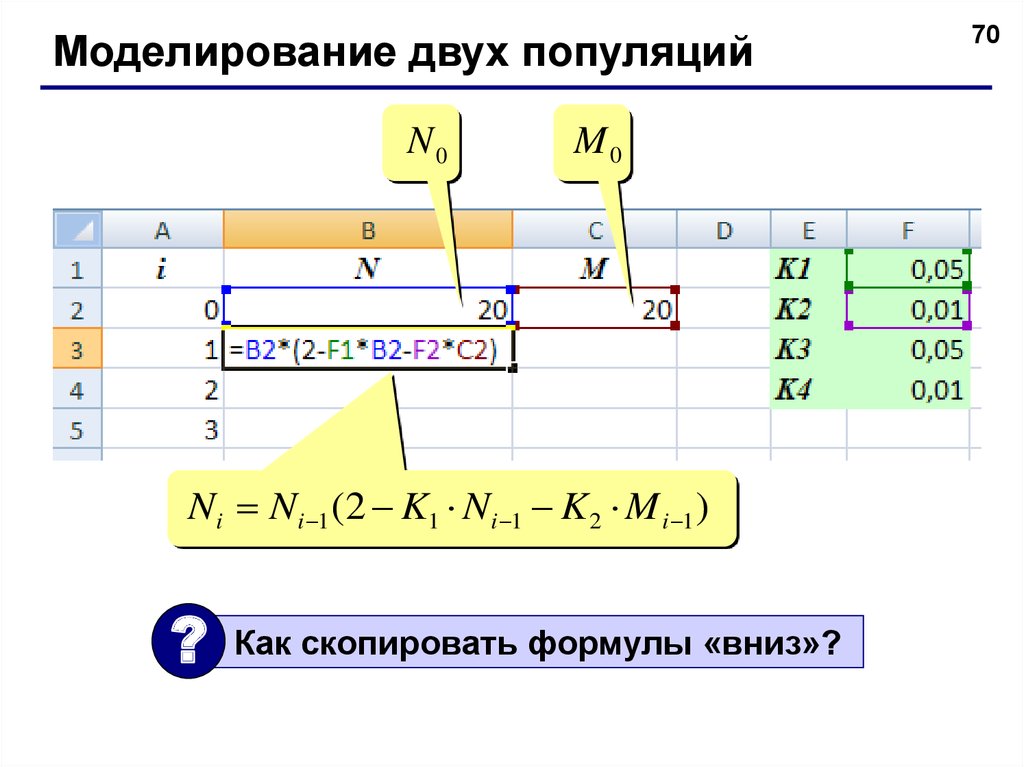
Моделирование двух популяций
N0
M0
Ni Ni 1 (2 K1 Ni 1 K 2 M i 1 )
?
Как скопировать формулы «вниз»?
70

71.

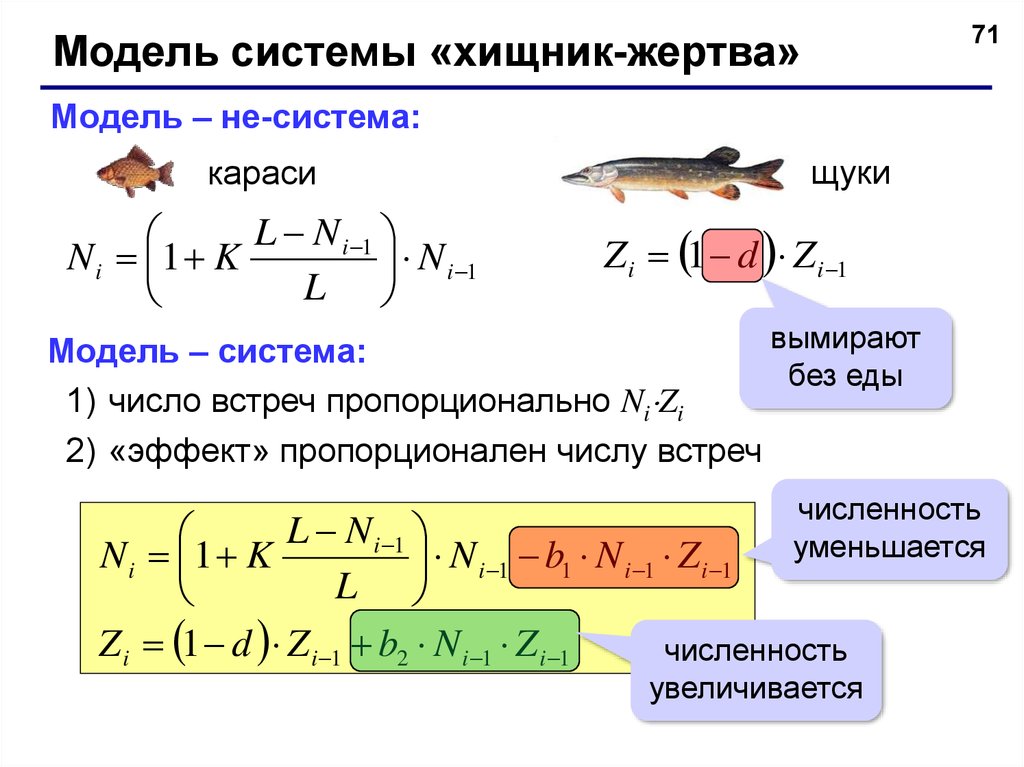
71
Модель системы «хищник-жертва»
Модель – не-система:
караси
L N i 1
N i 1 K
N i 1
L
щуки
Z i 1 d Z i 1
вымирают
Модель – система:
без еды
1) число встреч пропорционально Ni Zi
2) «эффект» пропорционален числу встреч
численность
уменьшается
L N i 1
N i 1 K
N i 1 b1 N i 1 Z i 1
L
Z i 1 d Z i 1 b2 N i 1 Z i 1
численность
увеличивается

72.

72
Модель системы «хищник-жертва»
Хищники вымирают:
Равновесие:
караси
Ni
Ni
Zi
Zi
щуки
i
i
d 0,8
d 0,8
b1 b2 0,5
b1 0,5;
b2 1

73.

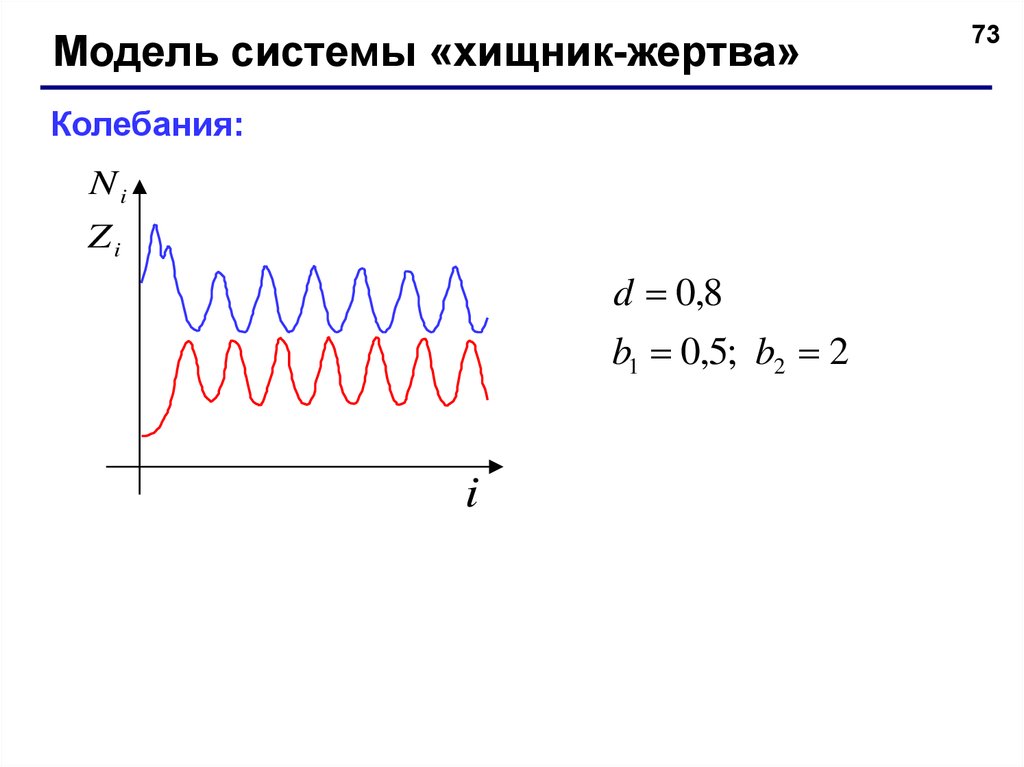
Модель системы «хищник-жертва»
Колебания:
Ni
Zi
d 0,8
b1 0,5; b2 2
i
73

74.

74
Случайные процессы
Случайно…
1) встретить друга на улице
2) разбить тарелку
3) найти 10 рублей
4) выиграть в лотерею
Как получить случайность?
Случайный выбор:
1) жеребьевка на
соревнованиях
2) выигравшие номера
в лотерее

75.

Случайные числа на компьютере
Электронный генератор
• нужно специальное устройство
• нельзя воспроизвести результаты
Псевдослучайные числа – обладают свойствами
случайных чисел, но каждое следующее число
вычисляется по заданной формуле.
Метод середины квадрата (Дж. фон Нейман)
564321
318458191041
458191
209938992481
938992
в квадрате• малый период
(последовательность
повторяется через 106 чисел)
75

76.

Случайные числа на компьютере
Линейный конгруэнтный метод
остаток от деления
xn (a xn 1 c) mod m
a, c, m - целые числа
xn (16807 xn 1 12345) mod 1073741823
230-1
простое число
?
Какой период?
период m
«Вихрь Мерсенна»: период 219937-1
76

77.

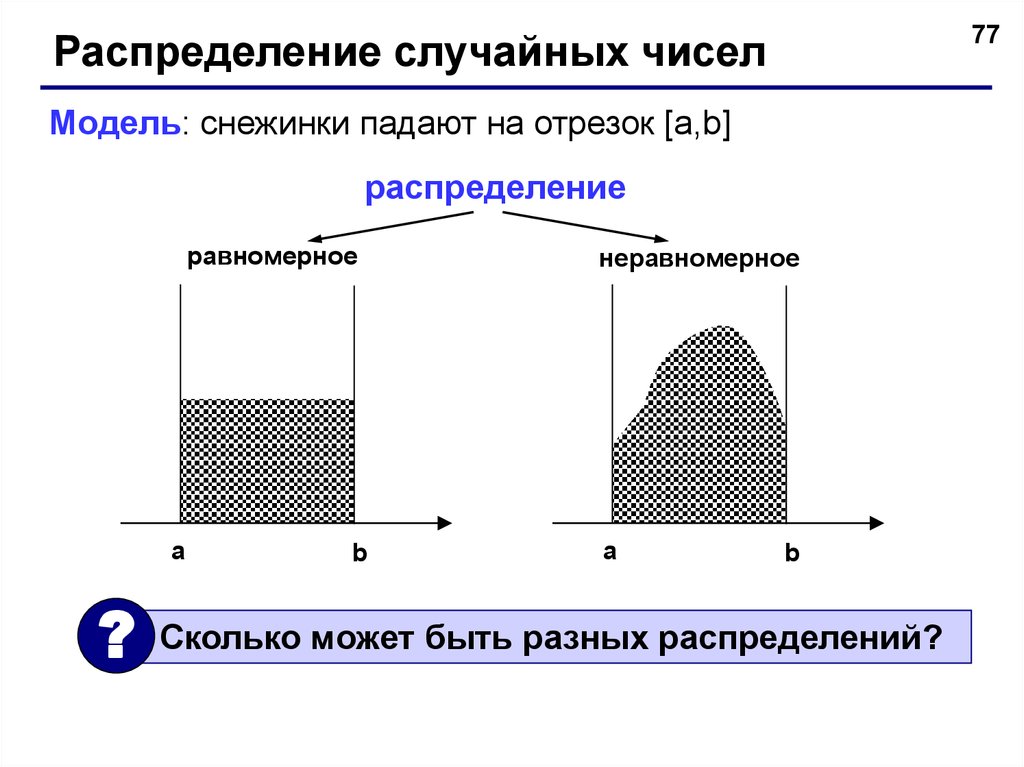
77
Распределение случайных чисел
Модель: снежинки падают на отрезок [a,b]
распределение
равномерное
a
?
b
неравномерное
a
b
Сколько может быть разных распределений?

78.

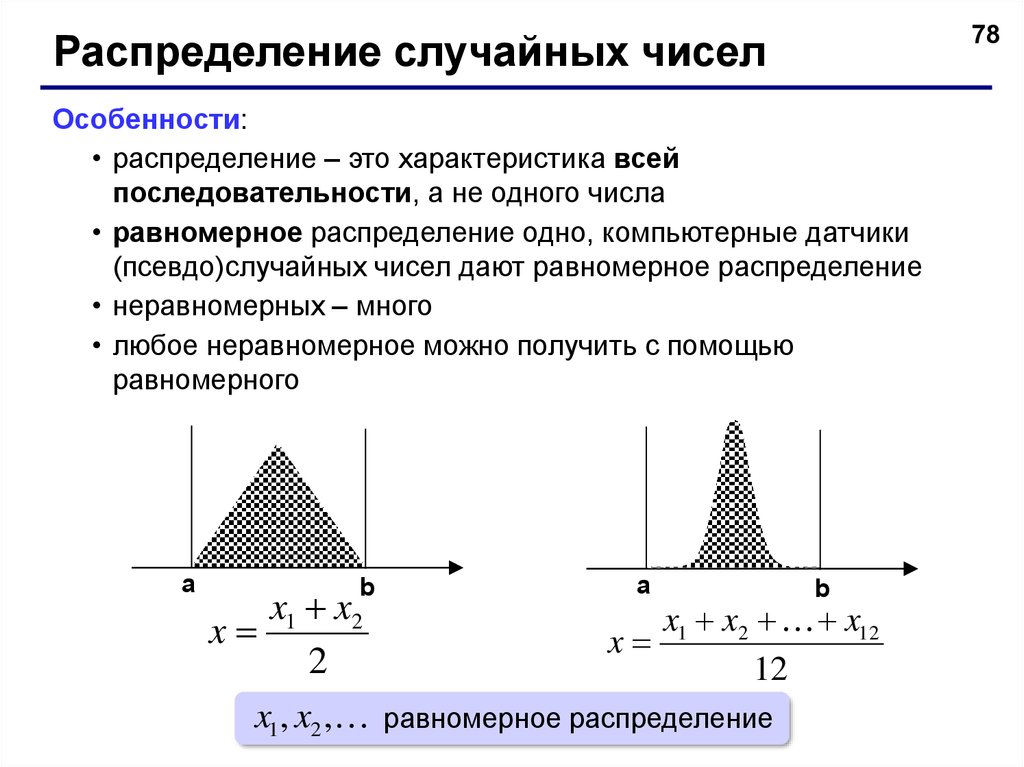
78
Распределение случайных чисел
Особенности:
• распределение – это характеристика всей
последовательности, а не одного числа
• равномерное распределение одно, компьютерные датчики
(псевдо)случайных чисел дают равномерное распределение
• неравномерных – много
• любое неравномерное можно получить с помощью
равномерного
a
b
x1 x2
x
2
a
b
x1 x2 x12
x
12
x1 , x2 , равномерное распределение

79.

Вычисление площади (метод Монте-Карло)
1. Вписываем сложную фигуру в
На фигуре M точек
другую фигуру, для которой
легко вычислить площадь
(прямоугольник, круг, …).
2. Равномерно N точек со
случайными координатами
внутри прямоугольника.
3. Подсчитываем количество
Всего N точек
точек, попавших на фигуру: M.
4. Вычисляем площадь: S
M
M
S0
!
N
S S0
N
1. Метод приближенный.
2. Распределение должно быть равномерным.
3. Чем больше точек, тем точнее.
4. Точность ограничена датчиком случайных чисел.
79

80.

Вычисление площади
R
(x,y)
R
Случайные координаты:
x := R*random;
y := R*random;
Когда точка внутри круга?
x2 y2 R2
Программа:
for i:=1 to N do begin
{ найти случайные координаты }
if x*x + y*y <= R*R then M := M+1;
end;
S := 4*R*R*M / N;
Как найти число ?
?
80

81.

Задания
«4»: Вычислите площади кругов c радиусами
R = 1, 2, 3, 4, 5.
Используя электронные таблицы, найдите
приближенную формулу для вычисления
площади круга.
«5»: Вычислите объем шаров c радиусами
R = 1, 2, 3, 4, 5.
Используя электронные таблицы, найдите
приближенную формулу для вычисления
объема шара.
81

82.

Броуновское движение
Случайное направление (в рад):
alpha := 2*pi*random;
Случайный шаг:
h := hMax*random;
Программа:
for i:=1 to N do begin
{ найти случайное направление и шаг }
x := x + h*cos(alpha);
y := y + h*sin(alpha);
end;
82

83.

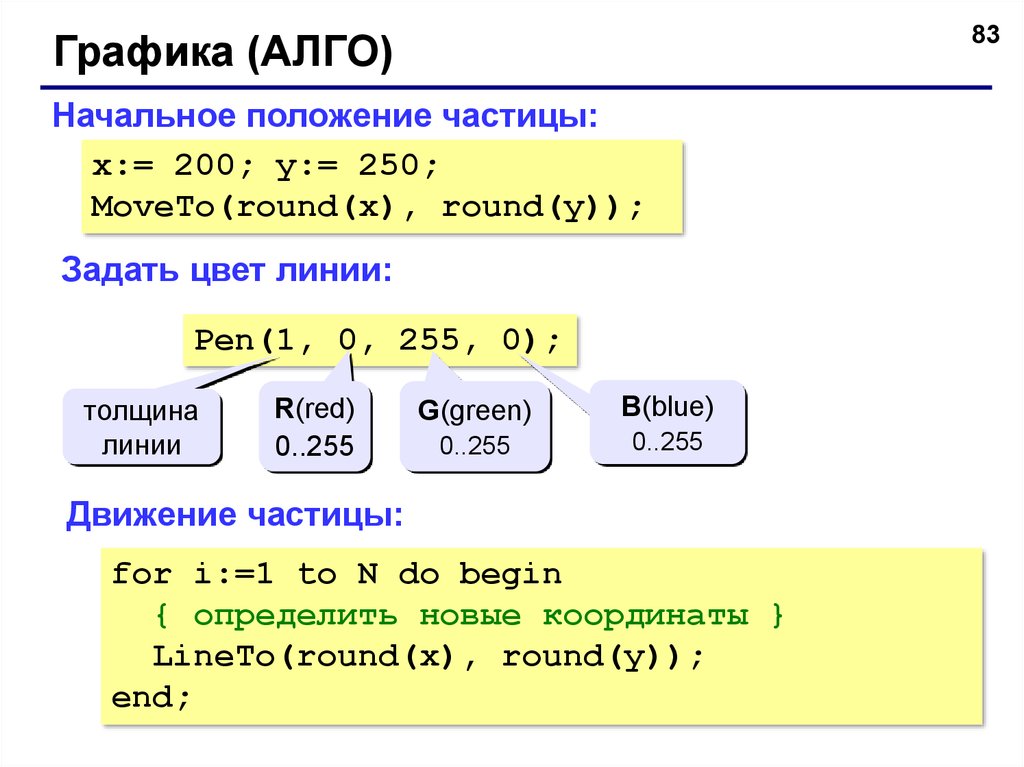
83
Графика (АЛГО)
Начальное положение частицы:
x:= 200; y:= 250;
MoveTo(round(x), round(y));
Задать цвет линии:
Pen(1, 0, 255, 0);
толщина
линии
R(red)
0..255
G(green)
B(blue)
0..255
0..255
Движение частицы:
for i:=1 to N do begin
{ определить новые координаты }
LineTo(round(x), round(y));
end;

84. Задания

Методы вычислений (Паскаль + Excel).
84
Задания
«4»: Постройте траектории движения двух частиц в
течение 200 шагов. Частицы должны двигаться
одновременно.
«5»: Постройте траектории движения 10 частиц в
течение 200 шагов. Частицы должны двигаться
одновременно. Используйте массивы для
хранения координат частиц.
К. Поляков, 2010-2011
http://kpolyakov.narod.ru

85.

Системы массового обслуживания
Примеры:
1) звонки на телефонной станции
2) вызовы «скорой помощи»
3) обслуживание клиентов в банке
сколько линий?
сколько бригад?
сколько операторов?
Особенности:
1) клиенты (запросы на обслуживание) поступают
постоянно, но через случайные интервалы времени
2) время обслуживание каждого клиента – случайная
величина
!
85
Нужно знать характеристики
(распределения) «случайностей»!

86.

86
Клиенты в банке
Вход клиентов:
1) за 1 минуту – до Imax человек
2) равномерное распределение
Обслуживание:
1) от Tmin до Tmax минут
2) равномерное распределение
?
Сколько нужно касс, чтобы клиенты
стояли в очереди не более М минут?

87.

87
Клиенты в банке
Число клиентов в помещении банка:
было
пришли
ушли
N := N + in - out;
!
Допущение: клиенты распределены по
кассам равномерно!
Количество касс: K
N
Средняя длина очереди:
K
Время ожидания:
Q – длина очереди
M Q Tmax
Допустимая длина очереди:
N
M
Qmax
K
Tmax

88.

88
Клиенты в банке
Пришли за очередную минуту:
округление
in := round(inMax*random);
Случайное время обслуживания:
T := Tmin + (Tmax – Tmin)*random;
!
1
Каждый оператор за эту минуту обслужит
T
клиентов!
Обслужены за очередную минуту и выходят:
out := round(K / T);

89.

Клиенты в банке (программа)
период моделирования L минут
count := 0; { счетчик «плохих» минут }
for i:=1 to L do begin
in := { случайное число входящих }
out := { случайное число обслуженных }
N := N + in – out;
if N/K > Qmax then
count := count + 1;
end;
writeln(count/L:10:2);
?
Что выводится?
89

90. Клиенты в банке (исходные данные)

Методы вычислений (Паскаль + Excel).
90
Клиенты в банке (исходные данные)
inMax := 10; { max число входящих за 1 мин }
Tmin := 1; { min время обслуживания }
Tmax := 5; { max время обслуживания }
L := 1000; { период моделирования в минутах }
M := 10; { допустимое время ожидания }
Задача: найти минимальное K, при котором время
ожидания в 90% случаев не больше M минут.
К. Поляков, 2010-2011
http://kpolyakov.narod.ru

91.

Конец фильма
91